非合作航天器的立体视觉位姿测量

束 安 ，裴浩东 ，周姗姗 ，段慧仙 ，陆佳琪

（1. 中国科学院智能红外感知重点实验室，上海200083；2. 中国科学院大学，北京 100049；3. 中国科学院上海技术物理研究所，上海200083；4. 中国科学院红外探测与成像技术重点实验室，上海200083）

1 引 言

近年来随着人类对太空探索的深入及全球对空间资源的持续开发与利用，空间碎片的数量急剧增加。例如2019 年印度进行了反卫星实验，美国国家航空航天局（NASA）表示该实验产生了约400 多块碎片，其中有24 块的轨道远地点超过了国际空间站所在轨道高度，给国际空间站和在轨卫星的正常工作造成了巨大的风险［1］。空间碎片一旦与正在服役的卫星航天器发生碰撞，会直接改变航天器的表面性能，导致航天器系统故障，对航天器的威胁极大。并且废弃的航天器还占用了宝贵的轨道资源，所以面向非合作航天器的在轨服务技术（On-Orbit Servicing，OOS）受到各国航天领域研究人员的重视［2-3］。

空间非合作航天器在轨服务的关键任务在于连续获取目标相对追踪系统的相对位置和姿态。随着立体视觉的发展，国际上以空间机器人进行空间在轨服务已成为一种必然趋势［4-5］。而视觉传感器作为空间机器人最主要的部分，成为了国内外航天机构的研究重点。2015 年，美国国防高级研究项目局（DARPA）在凤凰计划的基础上提出了“地球静止轨道卫星机器人服务”（RSGS），它采用多目视觉手段，在抓捕非合作航天器的逼近阶段，利用三目视觉算法实现对非合作目标的位姿测量，并计划于2022 年或2023 年发射［6-7］。2012 年，欧洲航天局（ESA）的 e.Deorbit 计划也属于清洁太空提倡工作，目的是开展针对欧洲环境卫星Envisat 的救援计划，该计划采用3 相机+2 激光雷达的组合构成用于自动操作的视觉系统，预计在2023 年执行首次主动碎片清除计划［8-9］。在国内，蔡晗针对非合作目标显著的矩形太阳能帆板和星箭对接环等，利用特征提取和最小二乘法椭圆拟合的方法进行双目视觉测量，并通过地面仿真验证了该方法在超近程阶段（小于4 m）的有效性［10］。杨宁等以航天器本体和星箭对接环作为识别特征，提出了立体视觉相对位姿自主测量方法，在航天器本体尺寸为0.28 m、相对距离为2 m 时位置测量精度小于4 mm，姿态测量精度小于 1.5°［11］。吴斌等针对含有圆和直线特征的1 m×1 m 航天器，将基于直线和椭圆检测单目算法嵌入到现场可编程门阵列（FPGA）和数字信号处理器（DSP）系统中，当距离小于4 m 时，距离方向精度优于10 cm，角度精度优于 1°［12］。综上所述，国外已将双目立体视觉技术应用到航天领域，但大多处于理论验证与样机研制阶段，而国内针对非合作航天器的双目视觉测量研究大多处在理论研究与计算机模拟仿真阶段，地面模拟实验不足。

本文提出一种对非合作航天器的双目立体视觉位姿测量方法。该方法采用两台大视场可见光相机获取高分辨率图像，用最大类间方差法（OTSU）和双边滤波法对图像进行预处理，接着利用弧线段拟合法提取目标表面的对接环椭圆，用Hough 变换提取目标的矩形边框特征，并引入极线约束准则、对接环尺寸约束和光流跟踪的方法，提高算法的提取精度和效率。该方法具有较高的位姿解算精度，可以为追踪航天器提供连续的位姿导航信息。

2 双目立体视觉位姿测量方法

图1 为本文双目立体视觉位姿测量方法的流程。其中，预处理在对图像进行去噪的同时，要保留边缘信息；对接环检测部分是通过弧线段拟合法，结合极线约束和尺寸约束提取目标的对接环椭圆；矩形边框检测部分是通过Hough 直线变换及光流法辅助跟踪检测目标的四条边框直线；最后通过立体视觉原理构建的对接环平面和边框角点建立目标坐标系，解算检测目标相对于世界坐标系的位姿关系。

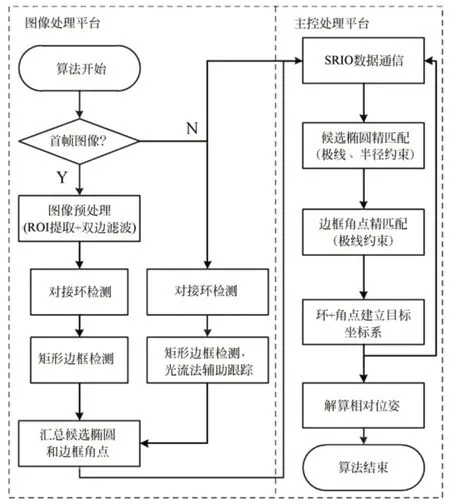
图1 双目立体视觉位姿测量流程Fig.1 Flow chart of binocular visual position and attitude measurement method

2.1 坐标系定义

为了方便解算非合作航天器与双目相机测量系统的位姿关系，建立目标坐标系（Op-XpYpZp）、左相机坐标系（Ol-XlYlZl）和世界坐标系（Ow-XwYwZw），如图2 所示。

2.1.1 目标坐标系（Op-XpYpZp）

该坐标系建立在非合作目标的表面，目标坐标系的原点Op位于对接环的中心，Xp轴为对接环平面的法向量，与相机光轴同向，原点Op指向边框角点的向量为Yp轴，对应右手准则得到Zp轴。

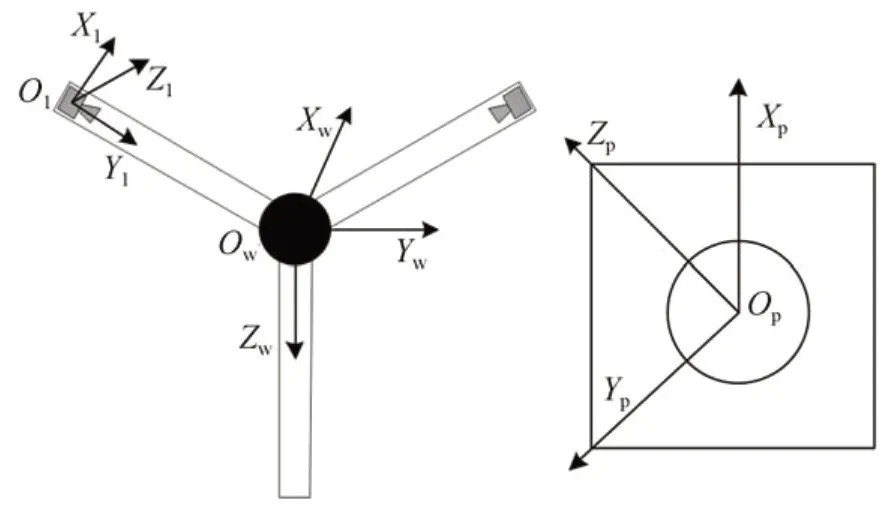
图2 双目视觉测量系统坐标系的相互关系Fig.2 Interrelation of coordinate systems of binocular vision measurement system

2.1.2 左相机坐标系（Ol-XlYlZl）

原点Ol定义为左相机的光心，Xl轴和Yl轴分别与图像的行和列平行。Zl轴为左相机的光轴，与图像平面垂直。

2.1.3 世界坐标系（Ow-XwYwZw）

世界坐标系定义在双目相机的安装支架上，以安装支架的中心为原点Ow，Xw轴为双目系统的逼近方向，Yw轴的方向为左相机光心指向右相机光心，对应右手准则得到Zw轴。文中的世界坐标系与左相机坐标系之间只存在刚体变换。

2.2 图像预处理

由于真实场景光照特性复杂，且非合作航天器表面材料特殊，相机在实际成像过程中，会存在噪声［13］。这些噪声叠加在原始图像上，不利于对接环椭圆和目标边框直线的检测，从而难以解算较高精度的位姿信息，所以在检测之前需要对图像进行预处理。一般大多采用滤波算法进行去噪处理，如均值滤波、中值滤波和高斯滤波等，这些滤波算法通过对邻域像素的加权平均来实现去噪的目的。但仅对图像进行空间域的处理，往往会在去噪的同时损失大量图像细节，使图像边缘过度平滑，丢失细节特征［14］。

本文选用双边滤波（Bilateral Filter，BF）法对左右图像进行预处理，该方法在高斯滤波器的基础上增加对像素之间相似度的判断，具有简单、非迭代和局域的特点，能够在保持图像边缘的基础上去除图像的噪声［15］。双边滤波法可定义如下：

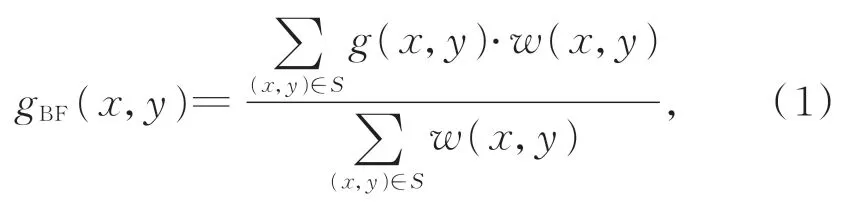
式中：gBF(x，y)为滤波后的结果，g(x，y)为原图像 (x，y)点的像素值，S表示 (x，y)点的掩膜集合，w(x，y)为滤波器的权重，其表达式为：

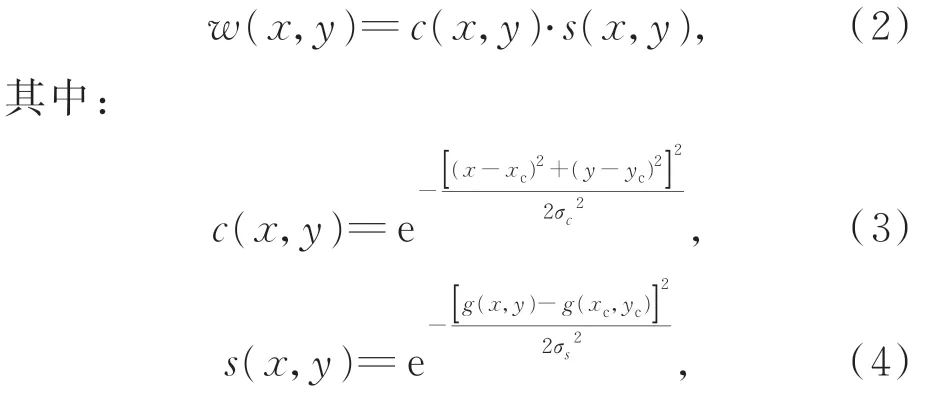
式中：(xc，yc)为掩模中心点，c(x，y)和s(x，y)分别表示空间域和值域的权重，σc和σs为2 个高斯函数核的标准差。所以，BF 法综合考虑了空间域和值域来分配权重，减少了图像边缘区域被过度平滑的现象，起到了保边降噪的作用。

为保证双目测量系统的实时性，本文在进行双边滤波前先通过最大类间方差法［16］快速计算图像的最优化阈值，以前景和背景的类间方差最大作为阈值选取准则，将图像分为前景区和背景区。然后建立包含前景（非合作目标本体）的感兴趣区域（Region of Interest，ROI），在该区域进行图像的预处理，提高双目测量系统的计算效率。图3 为非合作航天器显著特征进行图像预处理前后的对比，可以看出，滤波后目标表面的噪声得到了很好的去除，目标的边框信息更为突出，对接环边缘信息也得到了很好的保留。

图3 非合作目标双边滤波示意图Fig.3 Images of non-cooperative target after bilateral filtering

2.3 非合作航天器显著特征提取

在轨服务的近距离阶段，双目视觉测量系统受光照的影响，相机采集的图像信息较为丰富，但其中大部分并非位姿解算所需要的，所以需要从这些丰富的信息中提取显著的信息特征参与解算。本文研究的非合作航天器，通常表面含有星箭对接环、喷嘴、矩形边框和帆板等特征信息。由于帆板位于航天器两侧，很容易超出相机视场，而喷嘴的尺寸较小，所以本文通过提取目标表面的星箭对接环和矩形边框，建立目标坐标系，解算与世界坐标系的位姿关系，为追踪航天器提供精准的相对导航信息。

2.3.1 星箭对接环椭圆提取

根据相机成像原理，星箭对接环在双目相机像面上大多以椭圆形式呈现，常见的椭圆提取方法包括最小二乘法拟合、Hough 变换和基于圆弧段拟合［2］。基于最小二乘法拟合椭圆通常利用图像的边缘检测信息，要求所有参与计算的边缘点在同一个椭圆上，对于星箭对接环这种包含多个同心圆的目标适应性较差；Hough 变换则根据椭圆方程的 5 参数 (x0，y0，a，b，θ)，需要建立一个五维空间的累加器，不仅计算量大，且需要占用大量的内存资源，难以满足实时和嵌入式要求；基于圆弧段的椭圆拟合法根据弧段的特征将提取的边缘线段连接成弧段并分组，利用分组后的弧线段组进行椭圆参数的拟合。这种方法可以快速提取目标表面的多个椭圆特征，具有高鲁棒性、高效率等优点。

本文利用直线段检测（Line Segment Detector，LSD）算法［17］，快速从图像上提取亚像素级的线段，并根据线段的连续性和凸性分组得到弧线段组，对分组后的弧线段进行椭圆参数的拟合。基于LSD 弧线段的椭圆检测方法［18］的具体步骤如下：

（1）运用LSD 方法从原始图像中提取所有线段，得到去除直线段后的n条弧线段集合

（2）基于弧支撑线段的连续性和凸性原则，将属于同一曲线边缘的弧线段分为1 组，形成k个弧线段组

（3）对于弧线段组内的弧线段所跨角度较大时，直接进行最小二乘法拟合；对于所跨角度较小的组，进行两两组合拟合椭圆，最终得到初始椭圆集为初始椭圆集个数；

（4）运用椭圆类聚合算法对初始椭圆几何进行聚类分析，并应用椭圆的几何性质加以验证，产生候选椭圆集合。

图4 非合作目标候选椭圆Fig.4 Candidate ellipses of non-cooperative target

由于真实的空间环境较为复杂，且非合作航天器的对接环具有一定厚度和宽度，受光照角度的影响，图像上的圆弧段既来自凸出的对接环本身，也可能包含部分本体表面的环壁和阴影，从而拟合出多个椭圆特征，如图4 所示。为了筛选出正确的对接环，本文利用双目视觉的极线约束准则和对接环尺寸信息，建立完善的对接环筛选机制，具体步骤如下：

（1）对于左图上椭圆集合中的任一椭圆子集ei，计算圆心p(x，y)在右图上的极线li，F表示左相机与右相机之间的基础矩阵：

（2）计算右图上椭圆集合中的各个子集的圆心到极线li的距离{d0，d1，d2，...，dm}，若小于阈值t，则为候选匹配椭圆；

（3）计算候选匹配椭圆集中各子集对应的对接环半径，选取与真实半径最接近的一组，即为最终的对接环椭圆。

2.3.2 矩形边框提取

通过提取非合作航天器的对接环，可以解算出目标的相对位置、俯仰和偏航等信息，但是无法判断滚转维的信息，所以需要提取目标表面的显著特征，确定目标的滚转情况。由于空间环境背景纯黑，非合作航天器的边框直线特征更为突出。

本文通过Hough 变换提取非合作航天器的矩形边框特征，其基本思路是利用图像空间与参数空间点-线的对偶性，即对图像空间进行坐标变换，使它在另一坐标的特定位置出现峰值，从而将检测曲线转化为寻找峰值的问题［19］。为提高解算效率，通过极线约束准则和光流法辅助跟踪观测［20］，实现边框角点的选择以及优化角点提取算法，具体过程如下：

（1）对于初始帧，通过hough 变换提取非合作航天器的4 条直线边框，计算左右图像4 条直线边框的交点 ，分别为和通过双目极线约束准则，空间点P在左图像的位置pl时，相应的右图像匹配点pr必然在极线l上。所以通过极线距离约束，将4 个角点一一匹配，极线距离分别为{d0，d1，d2，d3}，选择极线距离最小时对应的角点，计算角点在世界坐标系下的三维坐标，参与建立目标坐标系。此外，将左右图像的4 个角点坐标作为光流法辅助跟踪的初始点集Pprev，并对滤波后图像进行裁剪，去除背景，提取ROI，下一帧只在该ROI 模板中进行边框角点提取，提高算法效率；

（2）对于非初始帧，以左图为例，根据ROI 模板提取当前帧的ROI，在区域内进行直线检测，并计算交点坐标表示当前帧数，辅以进行光流跟踪，得到光流跟踪的4 个角点坐标计算与检测点的像素距离选取离上一帧距离最近的交点，作为边框角点；当该帧的检测点与光流跟踪点之间的像素距离大于某一阈值（本文设置dmax=10.0）时，认为检测点异常，选择光流跟踪的点代替边框角点，从而提高双目视觉测量系统的稳定性。

2.4 非合作航天器位姿测量

根据双目视觉系统的坐标系定义（见图2），解算非合作航天器的位姿关系，即为计算目标坐标 系（Op-XpYpZp）相 对 于 世 界 坐 标 系（Ow-XwYwZw）的旋转矩阵假设对接环中心和边框角点在世界坐标系下的坐标为表示当前帧数，则目标坐标系的单位方向轴nx，ny和nz如 下 ：

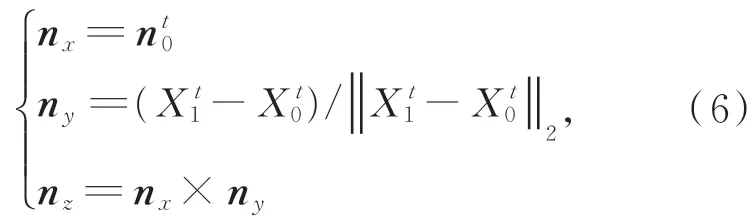
其中为对接环平面的法向量。则目标系相对于世界坐标系的旋转矩阵和平移向量为：

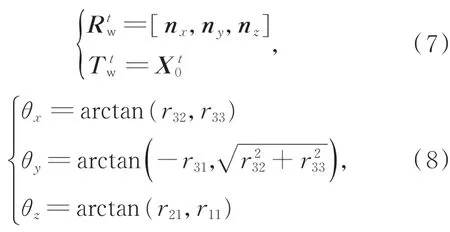
其中：θx，θy和θz分别为目标的三轴角度变化，rij(i=1，...3；j=1，...3)为旋转矩阵的对应元素。根据2.3.1 节和2.3.2 节的对接环和边框角点提取方法，可以计算出所以还需要重建出非合作目标的对接环平面，计算对接环平面的法向量。

如图5 所示，对于左图，过对接环圆心等角度绘制k条直线，则与对接环椭圆的交点为｛p1，p2，p3，...，p2k｝，以点p1为例，利用双目极线约束准则得到该点在右图上的极线为lp1，与右图上对接环椭圆的交点分别为pr0和pr1，通过立体视觉原理和与对接环圆心三维坐标的关系即可筛选出正确的匹配点。同理，可计算出左图所有点在右图上对应的点集为从 而求出对应点的三维点集｛P1，P2，P3，...，P2k｝。通过最小二乘法迭代计算对接环平面方程，得到对应三维圆的单位法向量。

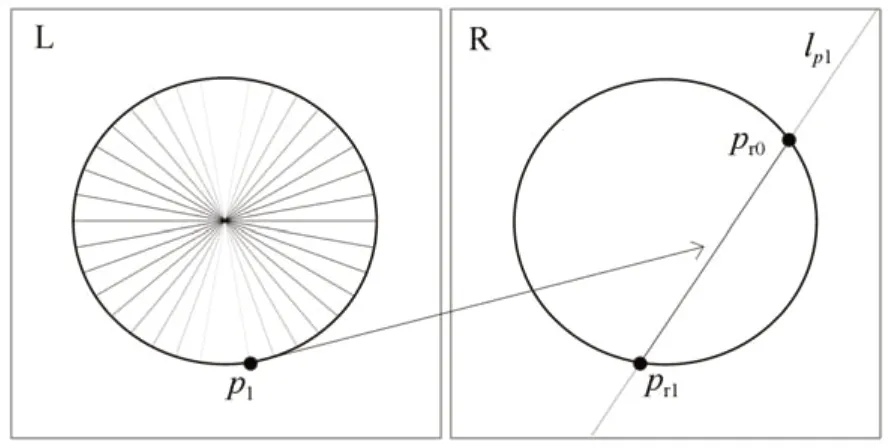
图5 双目立体视觉极线约束关系Fig.5 Relationship of polar constraint in binocular stereo vision

3 测量实验与结果

为了验证本文所提方法的有效性，本文选用2 台项目组研制的 60°×60°的大视场相机，探测器尺寸为2 048×2 048 pixel，像元尺寸为5.5 μm×5.5 μm，焦距为10 mm。为了获取更大的检测视场，两台相机的基线为1.3 m，并将光轴内旋18°。采用目前较为成熟的张氏平面标定法［21］，标定的重投影误差分别为 0.22 和 0.12 个像素。选用的非合作测量目标为2 m×2 m 的卫星模型，内环半径为60 cm。暗室环境下，测量模型与双目相机分别安装于两个六自由度的机械臂上，导轨长度为15 m，实验中使用0.1 个太阳常数的太阳模拟器作为光源，光线与测量模型的角度约为30°。双目视觉测量系统为嵌入式DSP6678 信息处理平台，主要分为左右2 个图像处理平台和1 个主控处理平台，图像预处理、对接环检测、矩形边框提取和光流法辅助跟踪在图像处理平台完成，主控处理平台利用极线约束和半径约束的方法进行候选椭圆的筛选和边框角点的提取，从而建立目标坐标系，解算非合作航天器的相对位姿信息。双目测量系统的数据更新率为1 Hz。

在某一状态下三目相机获取的图像如图6 所示。当前帧提取的对接环和矩形边框如图7所示。

图6 双目相机获取图像Fig.6 Images obtained by binocular camera

图7 非合作目标对接环和矩形边框Fig.7 Docking ring and rectangle borders of non-cooperative target

3.1 双目相机系统位置逼近实验

当追踪航天器距离非合作目标较近时，双目立体视觉系统能够在由远及近的逼近过程中连续为航天器提供位姿导航信息，是在轨服务的关键。本次实验中目标模型处于静止状态，双目相机系统在距目标12.0 m 处，以4 cm 每帧的速度向它逼近，运动到2.0 m 处停止，共获得251 帧图像。该组工况下非合作目标的绝对位姿和相对位姿变化如图8 所示。

从图8 可以看出，在双目相机系统向非合作目标匀速逼近的过程中，在远距离段（12.0～10.0 m）时，X轴的相对位置和姿态的波动较大，这是由于在远距离时，目标在双目图像上的成像较小，单个像元所占的真实尺寸较大，由于光照的不稳定，对接环和边框直线的检测精度比近距离时低，解算的相对位姿精度也较低，但波动最大不超过2 cm 和1°。总体来看，该方法在逼近实验中的输出结果较为稳定，具备近距离范围内连续的位姿解算能力。最终目标模型的三轴前后帧的相对位置测量标准差3σ=(0.958 cm，0.070 cm，0.082 cm)，相 对 角 度测 量 标 准 差 3σ=(0.223°，0.174°，0.409°)，算 法测量的移动距离均值为4.005 cm，与控制台提供的移动速度4 cm 每帧相差仅为0.05 mm，解算精度较高。

3.2 非合作目标模型姿态转动实验

实验过程中，双目相机系统在距模型4.0 m处静止，目标在机械臂的控制下以2.0°每帧的速度做匀速旋转，共采集68 帧图像。该组工况下非合作目标的绝对位姿和相对位姿变化如图9所示。

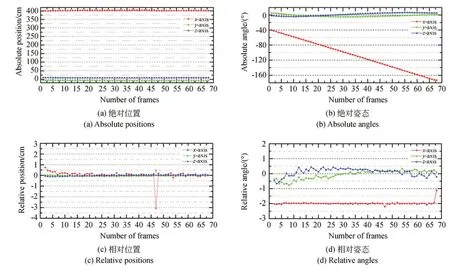
图9 4.0 m 处旋转非合作目标的绝对位姿和相对位姿变化Fig.9 Absolute and relative poses of non-cooperative target in rolling experiment at 4.0 m

从图9 可以看出，当目标在距双目相机系统4.0 m 处旋转时，双目立体视觉算法解算位姿趋势与实际运动状态一致，只有滚动轴角度匀速下降。由于目标姿态的改变，双目相机获取的前后帧图像受光照影响较大，所以容易干扰提取的对接环椭圆参数，所以其相对位置波动较大，如在第47 帧时，三轴的相对位置为（-3.057 cm，0.468 cm，0.016 cm），相对姿态为(-2.201°，0.134°，0.135°)，X轴对应的相对姿态误差较大。通过分析对接环和边框角点检测结果，造成该帧相对姿态误差较大的原因是右图部分阴影参与了拟合，导致最终构建的环法向量和圆心坐标突变。后期将通过前后帧的相对位置关系和进一步改进优化环检测方案，降低光照对算法的影响。总体来看，由于目标距相机较近，目标姿态的变化在图像上的体现越显著，像素点移动距离越大，相对姿态精度较高。最终目标模型的三轴前后帧的相对位置测量标准差3σ=(1.232 cm，0.201 cm，0.143 cm)，相对角度测量标准差 3σ=(0.106°，0.874°，0.726°)，算法测量的转动角度均值为1.991°，与控制台提供的转动速度2°每帧仅相差0.009°，解算精度较高。

4 结 论

本文针对在轨服务中非合作航天器相对位姿测量的关键任务，提出了一种双目立体视觉方法。该方法通过两台大视场相机获取图像，连续识别图像中的对接环椭圆和矩形边框，并引入极线约束准则、对接环尺寸约束和光流法跟踪的方法，提高算法的提取精度和效率。然后利用立体视觉构建非合作目标的对接环平面和边框角点，建立目标坐标系，解算与世界坐标系之间的位姿信息。最后通过实验室的双目相机、非合作目标模型和导轨平台，进行双目相机系统由远及近逼近和目标姿态转动实验。在双目相机系统12～2 m的逼近实验中，算法的相对位置精度优于1.0 cm，相对姿态精度优于0.41°，测量的移动距离均值为与真实移动距离相差0.05 mm。当目标在距双目相机系统4.0 m 处旋转时，算法的相对位置精度优于1.3 cm，相对姿态精度优于0.88°，测量的转动角度均值与真实转动角度相差为0.01°，解算精度较高。为了提升双目立体视觉测量方法的稳定性和适应性，后续要进行地面模拟实验，定量分析实验结果并优化和改进算法。