浅析光的单缝夫琅和费衍射
石仁斌,陈晓钊
(山东科技大学公共课教学部,山东 泰安 271019)
1 引言
光在传播过程中遇到障碍物时,能绕过障碍物的边缘继续前进,这种偏离直线传播的现象称为光的衍射现象。荷兰物理学家克里斯蒂安·惠更斯(Christiaan Huygens)提出次波的假设,以此来定性解释波的传播现象,并提出了惠更斯原理。法国物理学家奥古斯汀-让·菲涅尔(Augustin-Jean Fresnel)提出了“次波相干叠加”的概念,对惠更斯原理作了补充,提出了惠更斯-菲涅尔原理。为了简单形象地解释光的衍射现象,菲涅尔提出了“半波带”概念,给出了分析衍射现象的半波带法,半波带法能定量分析光的衍射。这种方法简单明了且运算不复杂,但是不精准、存在偏差。采用惠更斯-菲涅尔原理可以精确计算光的衍射,但是计算复杂。本文利用半波带法和惠更斯-菲涅尔原理法两种方法分析单缝夫琅和费衍射,并对两种方法进行比较。
2 单缝夫琅和费衍射
依照光源、衍射缝、屏三者的相互位置,可将衍射分成两种,一种叫做菲涅尔衍射,一种叫做夫琅和费衍射。图1所示为菲涅尔衍射(光源S和显示衍射图样的屏P,与衍射缝R之间的距离为有限远),图2所示为夫琅和费衍射(光源S和显示衍射图样的屏P,与衍射缝R之间的距离为无限远)。
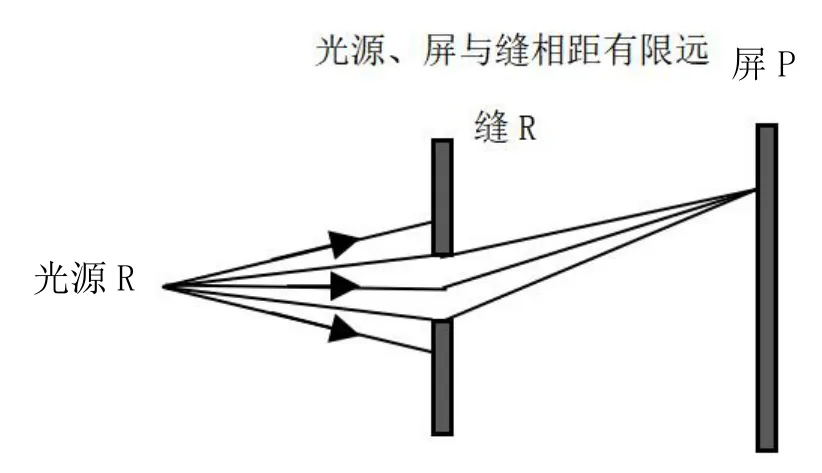
图1 菲涅尔衍射
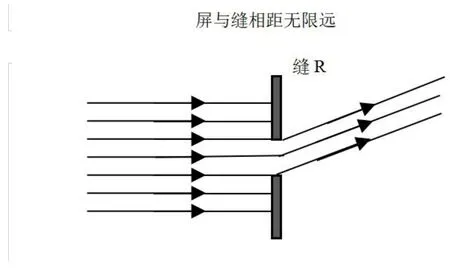
图2 夫琅和费衍射
3 用菲涅尔半波带法分析单缝夫琅和费衍射
3.1 惠更斯原理
在研究波的传播时,总可以找到同相位各点的位置,这些点的轨迹是一个等相面,称为波面。惠更斯曾提出次波的假设来阐述波的传播现象,从而建立了惠更斯原理。惠更斯原理可表述为:介质中波动传播到的各点都可以看作是发射次波的波源,而在其后的任意时刻,这些次波的包络就是新的波前。惠更斯原理可以解释光的直线传播、反射、折射和双折射等现象,但是它不能解释波的干涉和衍射现象。
3.2 惠更斯—菲涅尔原理
惠更斯原理可以解释光通过衍射屏时为什么传播方向会发生改变,但不能解释为什么会出现衍射条纹,更不能计算出条纹的位置和光强的分布。
菲涅尔根据惠更斯的“次波”假设以及波的叠加原理和干涉原理,提出了“次波相干叠加”的概念,从而对惠更斯原理作了物理性的补充。他认为,从同一波面上各点发出的次波是相干波,在传播到空间某一点时,各次波进行相干叠加的结果,决定了该处的波振幅。惠更斯原理进一步发展得出的原理就叫做惠更斯-菲涅尔原理。
根据菲涅尔“次波相干叠加”的设想,如果已知光波在某时刻的波阵面S,如图3所示,dS为某波阵面S上的任一面元,是发出球面次波的次波源,而空间任意点P的光振动,则取决于波阵面S上所有面元发出的次波在该点互相干涉的总效应。利用惠更斯-菲涅尔原理,可以对P点的光振动进行定量的计算,但运算比较复杂。对于单缝夫琅和费衍射,根据惠更斯-菲涅尔原理,可以对任意相干点的光振动进行定量计算。
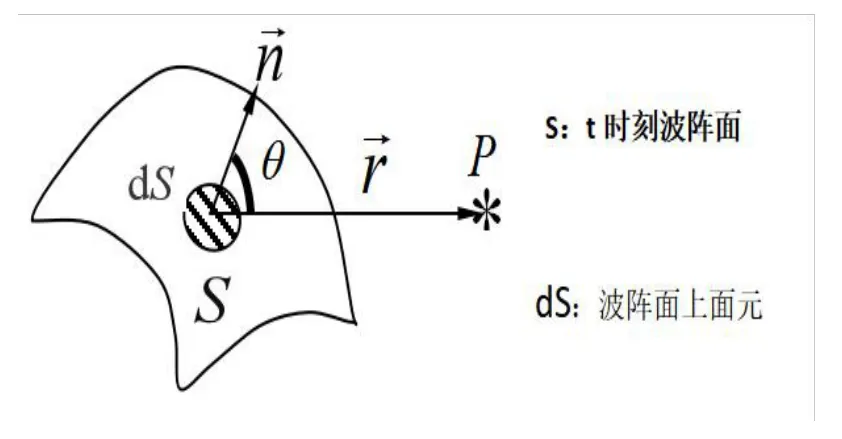
图3 次波相干叠加
3.3 用菲涅尔半波带法分析单缝夫琅和费衍射
图4 中所示,AB 为单缝的截面,其宽度为b。按照惠更斯-菲涅尔原理,波面AB 上的各点都是相干的次波源,次波射线与入射方向之间的夹角为θ,叫做衍射角θ。
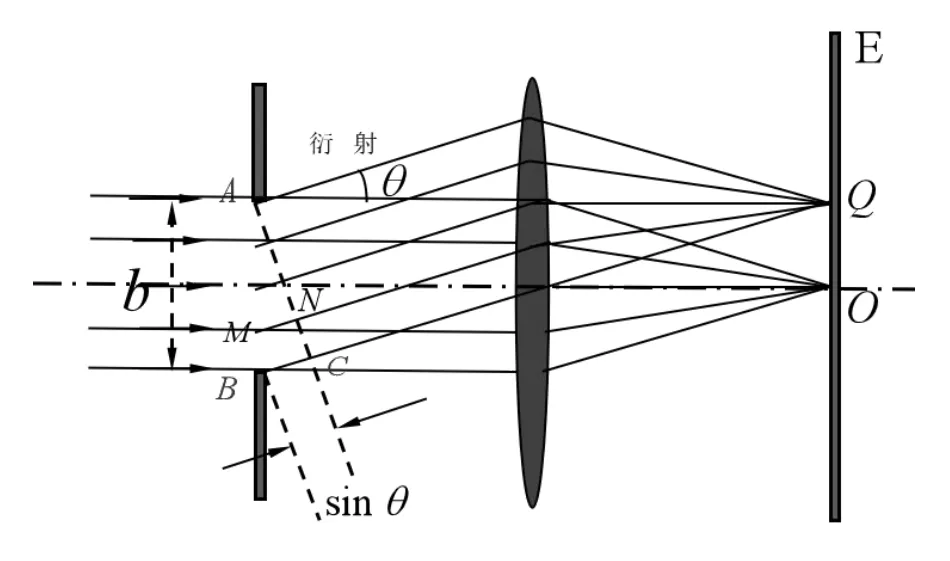
图4 单缝衍射条纹的位置
(1)沿入射光方向传播的各次波射线
沿入射光方向传播的各次波射线被透镜会聚于焦点O。由于AB 是同相面,而透镜又不会引起附加的光程差,所以它们到达点O时仍保持相同的相位而互相加强。这样,在正对狭缝中心的O处是一条明纹的中心,这条明纹叫做中央明纹。
(2)与入射光方向成θ角的次波射线
对于某确定的衍射角θ,设BC 恰好等于入射单色光束半波长的整数倍,即

这相当于把BC 分成k等分。作彼此相距的平行于AC 的平面,这些平面把波面AB 切割成了k个波带。可以近似地认为,所有波带发出的子波的强度都是相等的,且相邻两个波带上的对应点所发出的次波,在点Q 处的光程差均为,所以这种波带叫做半波带。于是,相邻两半波带的各次波将两两成对地在点Q处相互抵消,依次类推,偶数个半波带相互干涉的总效果是使点Q 处呈现为干涉相消。所以,对于某确定的衍射角θ,若BC 恰好等于半波长的偶数倍,即单缝上波面AB 恰好能分成偶数个半波带,则在屏上对应处将呈现为暗条纹的中心。对于某确定的衍射角θ,若BC 恰好等于半波长的奇数倍,即单缝上波面AB 恰好能分成奇数个半波带,则在屏上对应处将呈现为明条纹的中心。
综上所述,当平行单色光垂直单缝入射时,单缝衍射明暗条纹的条件为

根据暗条纹公式,有
当k=1 时,叫做第一级暗条纹,对应的衍射角θ1满足,;
当k=2 时,叫做第二级暗条纹,对应的衍射角θ2满足,;
当k=3 时,叫做第三级暗条纹,对应的衍射角θ3满足,;
……
根据明条纹公式,有
当k=1 时,叫做第一级明条纹,对应的衍射角满足,;
当k=2 时,叫做第二级明条纹,对应的衍射角满足,;
当k=3 时,叫做第三级明条纹,对应的衍射角满足,。
4 用惠更斯—菲涅尔原理法分析单缝夫琅和费衍射
4.1 衍射图样的光强
如图4 所示,平行光束垂直于缝的平面入射时,波面和缝平面重合。将缝分为一组平行于缝长的窄带,从每一条这样的窄带发出次波的振幅正比于窄带的宽度dx。设光波的初相位为0,b为缝的宽度,A0为整个狭缝所发出的次波在θ=0的方向上的合振幅,狭缝上单位宽度的振幅为A0dx/b,则狭缝处各窄带所发次波的振动可用下式表示:

这些次波都可认为是球面波,各自向前传播。首先对衍射角θ为的所有次波进行研究,在入射光束的平面波面AB 上各次波的相位都相等,光通过透镜L2 后在焦平面E 上的同一点Q 处叠加。作平面AC 垂直于衍射方向BC,根据AC 面上各点的相位分布情况即可确定在Q 点相遇的各次波的相位关系。从平面AC 上各点沿衍射方向通过透镜到达Q 点的光程相等,所以只要算出从平面AB 到平面AC 的各平行直线段之间的光程差就可以了。在图4 中,MN 为衍射角θ等于的任一条光线。令AM=x,则MN=xsinθ,这就是分别从M 和A 两点发出的次波沿与MN 平行方向到达平面AC 时的光程差。于是由(2)式得AC 面上N 点的光振动的表达式为:。
为简化计算,上式中假设各次波到达Q 点时有相同的振幅(不考虑振幅与光程成反比的关系以及倾斜因子)。根据惠更斯-菲涅尔原理,将上式对整个缝宽(从x=0 到x=b)积分,可得衍射角θ为的所有次波在观察点Q 叠加起来的合振幅:

令,故P 点的光强为

4.2 衍射图样的光强分布
当光屏放置在透镜L2 的焦平面上时,屏上出现衍射图样,光强的分布由(3)式决定。不同的衍射角θ对应于光屏上不同的观察点。首先来决定衍射图样中光强最大值和最小值的位置。即求出满足光强的一阶导数为零的那些点:

由此得sinu=0,u=tanu。
(1)单缝衍射光强中央最大值位置对应的衍射角θ。
由sinu=0,解得满足u0==0的那个方向,即 sinθ0=0,θ0=0。对应光强中央最大值的位置,即中央明纹位置。也就是在焦点O 处的光强为:I=,为最大值。这里,各个次波相位差为零,所以振幅叠加相互加强。
(2)单缝衍射光强最小值位置对应的衍射角θ。
由sinu=0,解得满足uk==kπ的这些衍射方向,即sinθk=(k=±1,±2,±3,···)(最小值位置)
k=±1,sinθ1=,对应第一级暗条纹中心位置;
k=±2,sinθ2=,对应第二级暗条纹中心位置;
k=±3,sinθ3=,对应第三级暗条纹中心位置;
……
(3)单缝衍射光强次最大位置对应的衍射角θ。
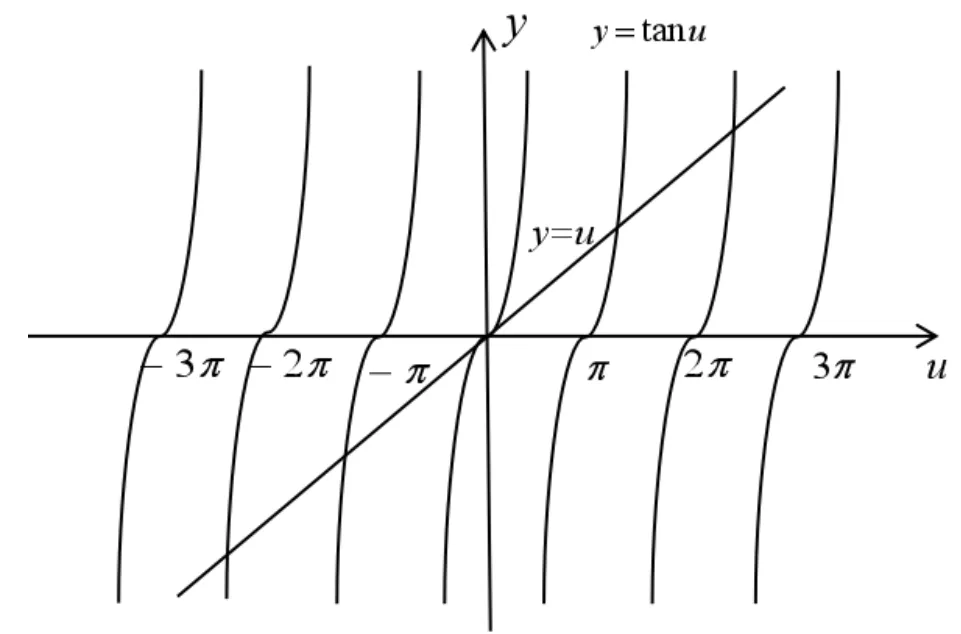
图5 直线y=u 和正切曲线y=tanu
在每两个相邻最小值之间有一最大值,这些最大值的位置可由超越方程u=tanu解得。可以用图解法求得u的值。作直线y=u和正切曲线y=tanu,如图6 所示,它们的交点就是这个超越方程的解:u=0,u1=±1.43π,u2=±2.46π,u3=±3.47π,u4=±4.48π,……
由此可得:分列于中央主最大两边的其他最大值(称为次最大)的位置为:
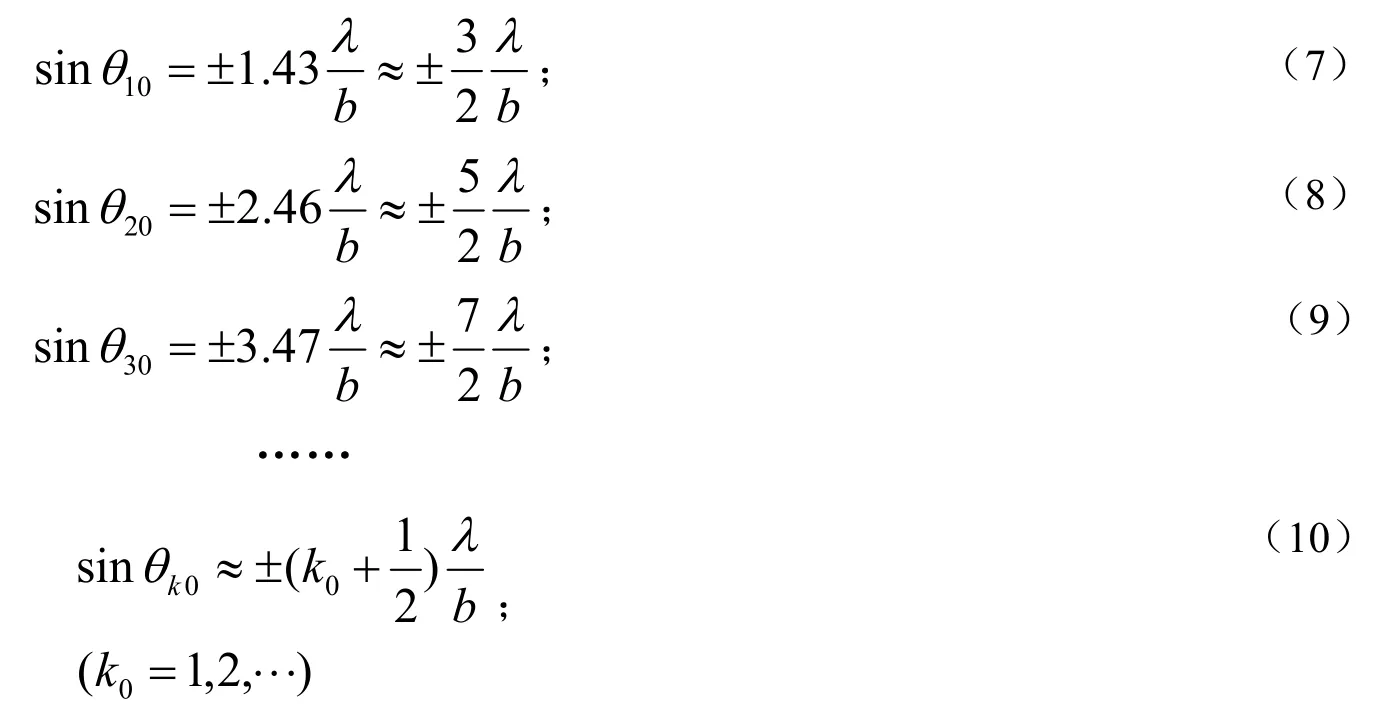
5 结束语
这里用半波带法和惠更斯-菲涅尔原理法两种方法解释单缝夫琅和费衍射现象。可以看出,半波带法简单明了,但有误差;惠更斯-菲涅尔原理法计算复杂,但精确。两种方法得到的结果非常接近,都能很好地解释单缝夫琅和费衍射现象。惠更斯-菲涅尔原理不是严格的理论产物,较大程度上是凭朴素的直觉而得到的。后来古斯塔夫·罗伯特·基尔霍夫(Gustav Robert Kirchhoff)和阿诺德·索末菲(Arnold Johannes Wilhelm Sommerfeld)根据一般的波动理论从理论上导出了与菲涅尔的公式十分接近的衍射公式。

