等效偏移距的转换波叠前时间偏移及其应用

陶建

上海市政工程设计研究总院（集团）有限公司，中国·上海 200082

1 引言

目前，叠前地震偏移已成为地震数据处理的主要方法。然而，对于复杂的介质，特别是在该地区散射比较发育时，传统的叠前偏移处理技术往往是无能为力的。等效偏移距方法是求解散射波场成像的基本方法之一，是一种很有潜力的叠前偏移方法。等效偏移距法在计算和分析上有以下优点：

（1）将克希霍夫偏移过程放到CSP 道集形成之后再计算，提高了计算效率和降低处理时间。

（2）CSP 道集的偏移距变化范围较大，覆盖率较高，信噪比较高，基本上包含了所有的偏移孔径地震数据。

（3）速度分析采用CSP 道集完成，速度谱能量聚焦变得更好，速度分析精度大大提高，而且在复杂地区提取速度更容易。

因此，研究基于等效偏移距的偏移方法具有一定的理论和实际意义。

近年来，中国和国际上的学者针对等效偏移距展开了很多的研究。Bancroft 和 Geiger 等人最早提出了等效偏移距（equivalent offset migration，EOM）的概念[1]。这种方法建立在散射波理论和克希霍夫叠前时间偏移原理上[2]，它将地震散射波的双平方根旅行时公式用一个等效偏移距的概念转换成了单平方根公式[3]，在转换后没有发生数据时移[4]。Fowler 证明双平方根方程可以简化成多种双曲线形式[5]，但EOM 方法是唯一没有引起时间改变的转换方法[6]。因此，我们可以利用等效偏移距将所有输入的地震道采样点以散射点为中心[7]，映射在给定的等效偏移距道上[8]，这个道集称为共散射点（CSP）道集[9]。CSP 道集聚集了所有可能的散射能量，它具有更高的覆盖次数和更大的偏移距范围[10]。其时距关系符合双曲线规律，而且其速度分析结果不受地层倾角的影响[11]。

2 原理

2.1 等效偏移距的定义

如图1所示，等效偏移距定义为并置的模型震源和模型接收点与共散射点在地面的投影位置之间的距离。求出的等效偏移距hε保持与最初的旅行时t 相等的总旅行时间2hε，从而旅行时间方程式变为：

同理，双平方根方程被修改成与等效偏移距旅行时间相关的方程，变为：

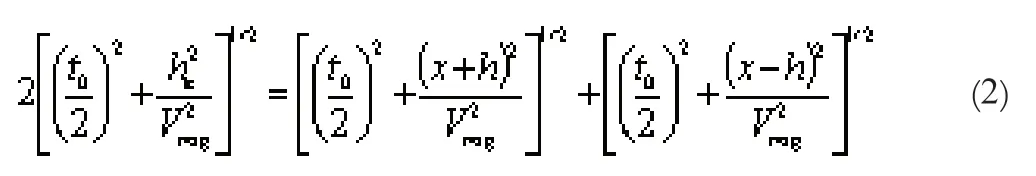
由上式解出等效偏移距hε，得：

图1 一个散射点的射线路径和旅行时

2.2 共散射点道集的形成

当把方程式（3）中的等效偏移距hε看成是的一个函数时，在处的一个输入样点将在固定时间沿着一条双曲线被映射到邻近的CSP 道集中。

现在讨论一个输入记录道的贡献，并设在此输入记录道里x 和h 的值是常量，输入采样从ta开始，逐点被映射到共散射点道集上。从图3可得到只有在ta时间后的一部分输入记录道向一个 CSP 道集贡献能量。在样本ta处的第一个有用能量来自与一个位于面的散射点处，并且根据下式来计算：

这里V0是表面处的速度。对于ta来说等效偏移距hεa由下式得到：

该输入道别的部分沿着偏移距单元依次进行分配直到分配到最大等效偏移距hεw，最大等效偏移距可由下式表示：

它是当t 趋于一个大值时该输入道等效偏移距的渐近值。

图2 将一输入道映射到一散射点道集上的示意图

每个记录道中的初始有用样本ta可以按照方程（4）来计算，初始等效偏移距hεa可以按照方程（5）来计算并被分配到一个合适的偏移距单元。在ta之后的样本被累加到这个等效偏移距单元中，直到等效偏移距hεi移动到下一个等效偏移距单元，在等效偏移距边界点上输入样本被累加到新的等效偏移距单元中。输入采样从一个等效偏移距单元移动到下一个等效偏移距单元的转变时间是ti，i 是等效偏移距单元号，可以重新整理方程（3）建立ti的方程式，表示为：

这里是hεi第i 个等偏移距单元的等效偏移距。

显然，对于一个输入道来说，最小等效偏移距和最大等效偏移距是已知的，而且等效偏移距间隔也是给定的。根据公式（7），等效偏移距按等间隔增大，而时间按不等间隔增大，并且增大的幅度逐渐增大。

图3 输入采样与CSP 道集的映射

因此，根据等效偏移距间隔和时间间隔之间的关系，把一输入道数据分成了若干小段，这些小段都有相应的等效偏移距与之对应。对每一个等效偏移距，把所有输入道数据与之对应的采样小段相互叠加起来，这样就形成了共散射点道集（如图4所示）。

图4 等效偏移距间隔和时间间隔关系示意图

2.3 转换波的等效偏移距

如图5中所示，hs，hr和hε分别是CCSP 表面位置到震源，接收点和并置震源—接收点的距离。hε是等效偏移距。假设共转换散射点（CCSP）的深度是Z0，P 波和S 波在这个深度的偏移速度分别为Vpimg和Vsimg（排版加一个“和”字放在Vping 和Vsing 中间），那么他们的偏移速度比表示为：

将（9）式表示为：

将方程（8）代入方程（10）解出等效偏移距hε，得：

图5 一个转换点的射线路径和旅行时

将方程（10）分解成两个方程：

从上述方程中解出：

将方程（14）代入方程（12）中，解出hε，得：

依据上述方程，观察出来等效偏移距与深度和速度有关。

3 模型计算及实际应用

利用等效偏移程序分别对以下简单模型进行计算。所用的转换波地震记录数据是用射线追踪正演的方法得到的地震数据。

3.1 凸起模型

凸起模型如图6所示。模型大小，纵、横波速度值如图6所示，纵横波速度比为2。道距，炮距，每炮96 道接收，共151 炮，炮点的起始位置在处。取 CCSP 间隔为，共有696 个CCSP 道集，在CCSP 道集中其转换波等效偏移距间隔为，其偏移剖面如图7所示。

图6 凸起模型

图7 凸起模型偏移剖面

3.2 凹陷模型

凹陷模型如图8所示。模型大小，纵、横波速度值如图8所示，纵横波速度比为2。道距，炮距，每炮96 道接收，共151 炮，炮点的起始位置在处。取 CCSP 间隔为，共有696 个CCSP 道集，在CCSP 道集中其转换波等效偏移距间隔为，其偏移剖面如图9所示。

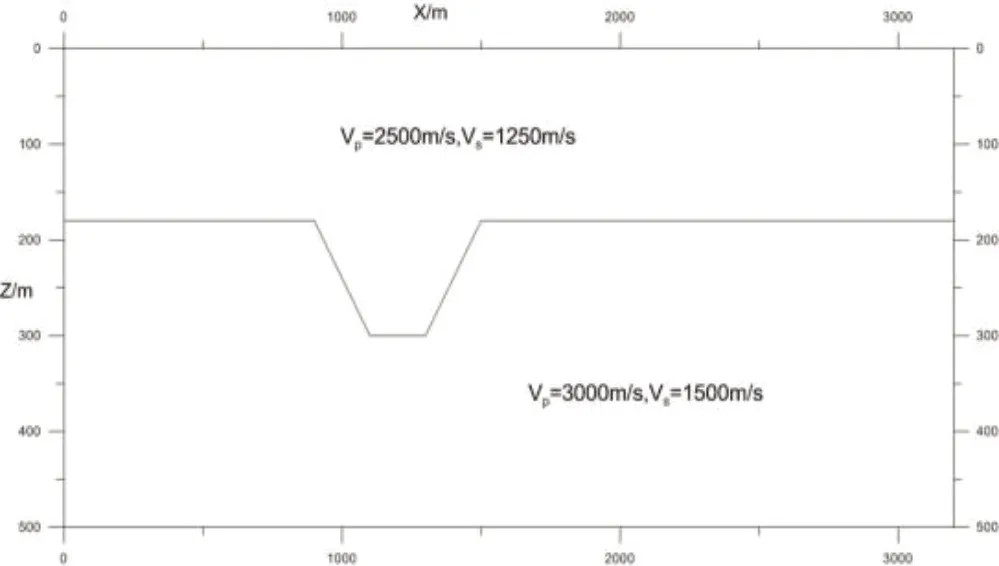
图8 凹陷模型

图9 凹陷模型偏移剖面

从图中所示可以看出，转换波等效偏移距偏移能进行正确成像。在偏移剖面中其同相轴成像较清晰，能够判断出地质体的位置和大致轮廓。

对某个油田的资料进行等效偏移距方法的实验，该区油气资源丰富，地层较为平缓，构造幅度小，小断层发育，奥陶系碳酸缝洞储集体发育，地震资料绕射波发育，难以准确成像。等效偏移距偏移方法的成像结果中反射层连续性更好，断层清晰，断点归位准确，缝洞能量的聚焦效果更好，绕射波的归位也更加准确，画弧现象不明显，信噪比高，偏移效果要明显优于常规的Kichhoff 叠前时间偏移结果。

4 结语

等效偏移距偏移方法的原理是克希霍夫时间偏移原理。它是根据散射理论，通过数学变化的方法巧妙地把震源—散射点—接收点的双平方根旅行时方程转化为以等效偏移距为变量的单平方根方程，在输入采样映射到以等效偏移距为变量的共散射点道集的过程中没有发生时移。

虽然等效偏移距偏移方法是在纵波数据模型下讨论提出的，但它同样适用于转换波的数据处理。通过对简单模型的计算，可以得到与之对应的偏移剖面，剖面可以大致反映出模型的形状和真实位置。、最后将该方法应用于塔河地区的实际资料处理中。

实际资料成像结果表明，与常规叠前时间偏移成像结果相比，等效偏移距叠前偏移剖面中，缝洞绕射波归位合理，缝洞边界、断层、断点成像清晰，横向分辨率高。