对接结构多部位损伤裂纹发生概率预测
叱 鑫,董登科,常文魁,张文东
(中国飞机强度研究所,陕西 西安 710065)
1 引 言
飞机结构中的广布疲劳损伤[1](Widespread Fatigue Damage,WFD)一般表现为多个机构细节处同时出现具有足够尺寸和密度的裂纹,从而使结构不再满足其损伤容限要求。多部位损伤(Multiple Site Damage,MSD)是WFD的一种,其特征是同一结构件中同时存在多条疲劳裂纹。随着疲劳裂纹在循环载荷的作用下互相影响并连通,飞机将不再满足剩余强度要求,从而可能产生灾难性的事故。
结构的广布疲劳损伤主要研究3个方面的问题:裂纹萌生、裂纹扩展以及剩余强度[2]。以往的研究多集中于MSD结构的裂纹扩展与剩余强度评估,有关MSD裂纹发生预测的问题关注较少。
薛景川[3]等提出了一种基于概率统计理论的MSD发生概率计算方法,可以通过单一细节疲劳寿命的分布特征,估算出多细节结构的MSD发生概率。Zhang[4]等根据单细节结构裂纹萌生寿命的概率,给出了多细节结构多条裂纹萌生概率的数值计算公式,并讨论了细节数量和应力水平对MSD发生概率的影响。王传胜[5]等提出了一种定量计算飞机结构发生多部位损伤可能性的方法,该方法认为当结构中有2个或2个以上细节发生裂纹时,结构发生多部位损伤,并给出了方法介绍和理论推导。奚蔚[6]等提出了一种广布疲劳损伤裂纹萌生寿命概率分布的分析模型,可以由单细节结构裂纹萌生寿命概率分布得到多细节结构中依次出现的各条裂纹萌生寿命的概率分布,并结合试验进行了验证。
根据疲劳应用统计学原理,可以认为结构细节疲劳寿命是服从对数正态分布的。本文在此基础上,通过材料典型元件的S-N曲线,结合正态分布的性质,得到广布疲劳损伤对接结构各细节处疲劳寿命的概率分布,并利用蒙特卡罗模拟预测了广布疲劳损伤对接结构孔边出现MSD裂纹的先后顺序。图1所示为本文的研究内容及流程。

图1 对接结构MSD裂纹发生概率预测内容与流程
2 典型元件S-N曲线试验
试验采用2524-T3铝合金材料,试验件的厚度为1.6mm,共33件。试验件尺寸如图2所示。
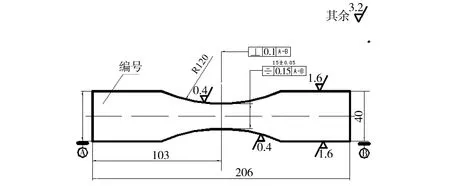
图2 2524-T3试验件几何尺寸
采用INSTRON1332疲劳试验机(如图3所示),进行320MPa、280MPa、250MPa、220MPa、200MPa、180MPa、160MPa等7个不同应力水平下的试验。每个应力水平下,试验件的数量为4~5件。试验结果如表1所示。

图3 INSTRON1332疲劳试验机

表1 2524-T3试件试验结果
根据疲劳统计学原理[7],结构的疲劳寿命服从对数正态分布,其概率密度为:
(1)
取同一应力水平下一组寿命的对数均值和对数方差为μ和σ,则μ即为该应力水平下50%可靠度的疲劳寿命。根据正态分布(见图4)性质[8]:

图4 正态分布
P{|X-μ|≤2σ}=0.9544
(2)
即95%的数值是在距离平均值两个标准差之内,从而得到该应力水平下95%可靠度的疲劳寿命μ0=μ+2σ,如表2所示。拟合得到50%可靠度和95%可靠度的2524-T3材料典型元件S-N曲线,如图5、图6所示。

表2 典型元件疲劳寿命的对数均值和对数方差

图5 50%可靠度2524-T3材料典型元件S-N曲线

图6 95%可靠度2524-T3材料典型元件S-N曲线
3 对接结构孔边细节处寿命概率密度
本文的研究对象为对接平板结构,如图7所示,板宽为250mm,上板厚为2.29mm,下板厚为1.8mm,上下板由铆钉连接,孔径为5mm,列间距ρ=20mm。

图7 试验件几何尺寸
由文献[9]可知,单细节处裂纹疲劳寿命服从对数正态分布,含相似多细节结构中,对于n个相互独立的细节,每个细节所承受的应力水平大小不同。假设结构中各细节相互独立,且相互之间不发生影响,则其裂纹疲劳寿命的概率密度分别为f1(x),f2(x),…,fn(x)。
确定疲劳寿命的概率密度,只需确定对数正态分布的两个参数,即均值μ和方差σ。其中,均值μ的确定是根据应力严重系数对有限元模拟对接结构各细节处的应力值进行修正,并结合50%可靠度2524-T3材料典型元件S-N曲线得到,方差σ的确定可由正态分布的性质结合50%和95%可靠度2524-T3材料典型元件S-N曲线得出。
3.1 内力分布计算
图8为简单连接件的受力状态,可以看出,当外载传递到铆钉孔附近时,传递方式分为钉传载荷和旁路载荷。

图8 简单连接件及其受力状态
由文献[10]可知,连接件内力公式:
(3)
式中,R为钉传载荷;P为外载;C为紧固件弹性段的柔度系数;Fsh为上板的弹性柔度系数;Fxi为下板的弹性柔度系数。
上板柔度系数:
Fsh=ρ/(WtshE)
(4)
下板柔度系数:
Fxi=ρ/(WtxiE)
(5)
单面搭接件的紧固件柔度系数:
(6)
式中,D为紧固件直径;t1为较薄板的厚度;t2为较厚板的厚度;E为板弹性模量;Kdc为紧固件材料修正系数,对于铝钉,Kdc=1。
代入公式求得:
C=7.3×10-5(mm/N)
(7)
计算得到钉传载荷:
(8)
旁路载荷:
(9)
3.2 应力严重系数
拉伸疲劳载荷下的应力严重系数[10]计算公式:
(10)
由内力分布计算可知,该连接件最外端一排孔为最危险细节,查阅文献[10],将α=1.1(钻孔)、β=0.75(铆钉)、Sck·n=312.5MPa、Kjy≈1.05、PR1=4.13kN、D=5mm、t=1.8mm、θ≈1.4、Ktn≈2.4、PP1=9.37kN、W=250mm代入公式(10),可得:
SSF≈2.0
(11)
3.3 疲劳寿命对数均值μ和方差σ的确定
利用有限元软件Abaqus对试验件进行模型建立(见图9),并进行疲劳拉伸模拟,带板与蒙皮之间使用梁单元MPC连接模拟铆接连接。根据应力云图显示,选取应力较大的外端一列孔为研究对象,得到各个孔边细节处平行于外载方向的应力S11。根据前文中得到的应力严重系数SSF≈2,对孔边细节处应力值进行修正,得到修正后应力值。

图9 试验件有限元模型
(12)
将前文中得到的50%和95%可靠度的S-N曲线放在同一坐标系中,如图10所示。
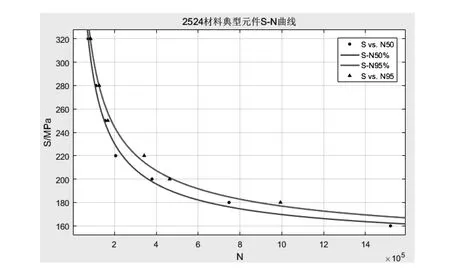
图10 50%和95%可靠度材料典型元件S-N曲线
95%可靠度疲劳寿命的均值为:
μ0=μ+2σ
(13)
图11为试验件孔的编号。对于1号孔左细节处,取同一应力水平在图中作水平线,与两条曲线交点的横坐标差值即为2σ,从而得到裂纹疲劳寿命在该应力水平下的对数方差σ,如图12所示。

图11 试验件孔编号

图12 1号孔左细节处在S-N曲线上的值
表3为各细节处寿命的对数均值和对数方差,以1号孔左细节处为例,由表3中数据可得该细节处对数寿命的概率密度为:

表3 对接结构疲劳寿命的对数均值和对数方差
(14)
4 蒙特卡罗模拟预测裂纹发生顺序
蒙特卡罗[11](Monte-Carlo)法又称随机抽样技巧或统计试验方法,是以概率统计理论为基础,利用随机模拟和统计试验的方法求某些数学、物理和工程问题近似解的数值方法,基本思想是通过随机抽样试验,得到所求问题发生的概率。
疲劳寿命的对数破坏概率分布函数为:
(15)
在该对数正态分布中,若有:
P{X≤xa}=α
(16)
则称xa为X的下侧分位数。由正态分布性质可得:
F(xa)=P{X≤xa}=α∈[0,1]
(17)
利用蒙特卡罗方法,在[0,1]区间内随机取10000个点作为F(x)的值,其意义即为产生裂纹的概率P。调用MATLAB中的norminv函数:
X=norminv(P,mu,sigma)
(18)
可求得对数正态分布中10000个随机不同F(x)值对应的下侧分位数,这些下侧分位数即为裂纹随机生成的10000个发生概率对应的疲劳寿命。
MATLAB中的norminv函数如图13所示。利用图13中的方法对20个细节处的发生概率分别进行10000次抽样,得到各细节处裂纹多个发生概率对应的寿命,对比相同概率下20个细节处的裂纹发生寿命,统计多个样本中裂纹疲劳寿命最小的细节处的频数,可估算出最先开裂的细节处位置。

图13 Matlab中的norminv函数
同一概率中的10000个样本,最小疲劳寿命的数量最多的为1号孔右细节和10号孔左细节,则认为该对接结构最先可能发生疲劳裂纹的孔为1号和10号孔,说明越靠近边缘的孔产生疲劳裂纹的概率越大。
5 对接平板拉-拉疲劳试验
5.1 试验情况
试验采用平板矩形带板连接的连接件,如图14所示。带板材料为2024-T3,厚度2.5mm,蒙皮材料为2524-T3,厚度1.8mm,件数12件。选择1000kN疲劳试验机进行试验,试验应力与载荷谱见表4。

表4 试验应力与载荷谱

图14 试验件示意图
5.2 试验结果
按照载荷谱进行试验,根据图15中的编号记录最先出现裂纹的位置,见表5。

图15 试验件孔编号

表5 试验件最先出现裂纹的位置
取远端一列孔进行研究,位置编号为A、B、C、D、E、F,统计出现裂纹的位置次数,见图16。

图16 出现裂纹的位置统计
由表5和图16可以看出,两端的孔比中间的孔更容易开裂,预测值与试验值接近;越靠近边缘的孔,最先开裂的概率越大,并且开裂概率从边缘向中间逐渐降低。
6 结 论
本文根据疲劳统计学原理,基于由应力严重系数修正的S-N曲线及正态分布性质,得到对接平板共线孔边细节处裂纹疲劳寿命的概率分布,并利用蒙特卡罗模拟预测了广布疲劳损伤对接结构孔边出现MSD裂纹的先后顺序,给出了相应的理论推导,得出的结论为越靠近边缘的孔产生疲劳裂纹的概率越大,试验结果与理论预测相吻合。

