Coherent H∞ Control for Linear Quantum Systems With Uncertainties in the Interaction Hamiltonian
Chengdi Xiang, Shan Ma, Sen Kuang, and Daoyi Dong
Abstract—This work conducts robust H∞ analysis for a class of quantum systems subject to perturbations in the interaction Hamiltonian. A necessary and sufficient condition for the robustly strict bounded real property of this type of uncertain quantum system is proposed. This paper focuses on the study of coherent robust H∞ controller design for quantum systems with uncertainties in the interaction Hamiltonian. The desired controller is connected with the uncertain quantum system through direct and indirect couplings. A necessary and sufficient condition is provided to build a connection between the robust H∞ control problem and the scaled H∞ control problem. A numerical procedure is provided to obtain coefficients of a coherent controller. An example is presented to illustrate the controller design method.
I. INTRODUCTION
CONTROLLING quantum phenomena plays an important role in developing quantum technologies, and the exploration of quantum system control theory has drawn wide interests from scientists and engineers in different fields, such as physical chemistry, quantum optics, and quantum information [1]–[8]. In particular, robustness has been recognized as a key issue in the development of quantum control theory and practical quantum technology since the existence of various types of uncertainties and disturbances is unavoidable for most practical quantum systems. These uncertainties may come from decoherence, systematic errors,environmental noises or Hamiltonian identification inaccuracies [9]–[13]. Hence, to deal with different kinds of uncertainties in quantum systems, it is important to develop robust control methods [14]–[31]. For example, a samplingbased learning control (SLC) method has been applied to controller design of quantum systems with uncertainties, even when the uncertainty parameters have large fluctuations [19],[20]. In [21], sliding mode control has been proposed for twolevel systems with bounded uncertainties in the Hamiltonian and can guarantee the desired robustness in the presence of uncertainties. A two-step strategy by combining the concepts of feedback and open-loop control methods is presented in[22] to achieve stabilizing control of quantum systems with uncertainties. A sequential convex programming method is proposed in [23] to design robust quantum gates. A noise filtering approach is applied in [24] to enhance robustness in quantum control.
As an effective robust control method, H∞control [32], [33]has been used in the quantum domain [25]–[29]. James et al.[25] have formulated and solved an H∞controller synthesis problem for a class of linear stochastic systems to bound the undesirable effects of disturbance on performance. In [26], the coherent H∞control method is applied to a quantum passive system, which is modeled purely in terms of the annihilation operator but not the creation operator. While studies [25], [26]only consider the disturbance input, [27] further investigates coherent robust H∞control including disturbance input and parameter uncertainties. A sufficient condition was presented to build the relationship between the robust H∞control problem and the scaled H∞problem. The work [28] extends the result in [27] to a class of quantum passive systems. It should be noticed that most of the studies [25]–[28] consider the coherent H∞control with indirect coupling. The direct and indirect couplings in coherent H∞feedback control of linear quantum systems are studied in [29].
In this paper, we present coherent H∞control for quantum systems with direct and indirect couplings by taking interaction Hamiltonian uncertainties into consideration. The contributions of this paper are summarized as follows. This paper considers the uncertainties in the interaction Hamiltonian, while most existing papers have only considered the uncertainties in the system Hamiltonian or in the coupling operators [21], [27], [30]. To build a connection between the robust H∞control problem and the scaled H∞control problem, a necessary and sufficient condition is provided rather than only a sufficient condition given in [27], [28]. This paper also considers the effect of direct and indirect couplings between a quantum system and a coherent controller, instead of only the indirect coupling [25], [26]. Also, a numerical procedure for robust coherent controller design is provided based on the change of variable technique, linear matrix inequality (LMI) method [34] and multi-step optimization method.
This paper is organized as follows. In Section II, a class of linear quantum systems via direct and indirect couplings with an exosystem is introduced using quantum stochastic differential equations (QSDEs) and parameters (S,L,H). Then,uncertainties in the interaction Hamiltonian are described. In Section III, for this class of uncertain quantum systems, a robustly strict bounded real condition without uncertainties is presented through a necessary and sufficient condition. In Section IV, a coherent robust H∞controller design method is proposed using robustly strict bounded real lemma. In Section V, a numerical procedure to obtain the corresponding coefficients of desired controller parameters is proposed.Also, an example is presented to illustrate the method in Section V-C, followed by the conclusion in Section VI.
Notations:
In this paper, Imdescribes an m×m identity matrix and 0m×ndescribes an m×n zero matrix, where the subscript is omitted when m and n can be determined from the context. Define
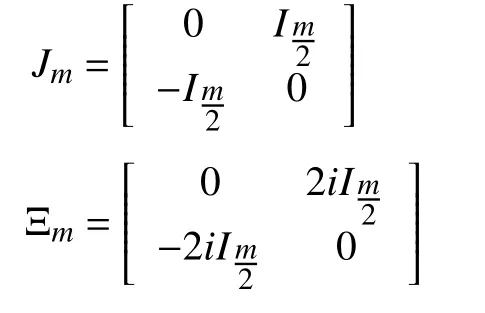
and
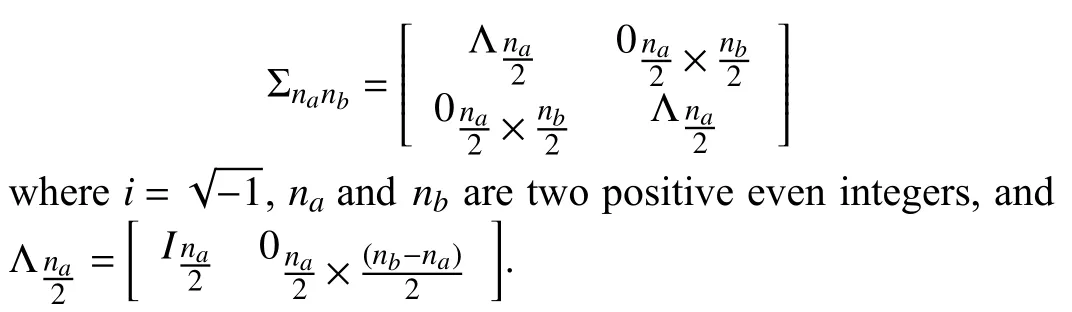
II. QUANTUM SYSTEM MODEL
A. A Class of Quantum Stochastic Systems
Consider an open quantum system interacting with an exosystem via indirect and direct couplings, which are affected through field couplings and interaction Hamiltonian.This class of quantum system models can be described in the quadrature form by the following non-commutative quantum stochastic differential equations (QSDEs) [29]:


B. Uncertain Perturbations in the Interaction Hamiltonian
This paper considers the class of uncertain quantum systems subject to uncertain perturbation in the interaction Hamiltonian. The corresponding uncertain interaction Hamiltonian Hintcan be denoted as follows:







VI. CONCLUSION
This paper has considered a class of quantum systems with uncertainties in the interaction Hamiltonian. This class of systems interact with exosystems through direct and indirect couplings. For a given disturbance attenuation, a robustly strict bounded real condition for this class of uncertain quantum systems is given. A necessary and sufficient condition of H∞analysis for the quantum systems is proposed. Moreover, a coherent robust H∞controller design method for this class of uncertain quantum systems via direct and indirect couplings is studied. A necessary and sufficient condition was provided to convert this robust H∞control problem into a scaled H∞problem. To obtain coefficients of a coherent controller, a numerical procedure is presented by using LMI formulation, multi-step optimization and physical realizability conditions. As a future research direction, we may focus on other types of uncertainties and develop new methods for robust controller design of these uncertain systems. Another interesting idea is to extend the robustness results to the framework of the Kalman decomposition for linear quantum systems [49].
 IEEE/CAA Journal of Automatica Sinica2021年2期
IEEE/CAA Journal of Automatica Sinica2021年2期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- Physical Safety and Cyber Security Analysis of Multi-Agent Systems:A Survey of Recent Advances
- Joint Algorithm of Message Fragmentation and No-Wait Scheduling for Time-Sensitive Networks
- Multiagent Reinforcement Learning:Rollout and Policy Iteration
- A Survey on Smart Agriculture: Development Modes, Technologies, and Security and Privacy Challenges
- A Survey of Evolutionary Algorithms for Multi-Objective Optimization Problems With Irregular Pareto Fronts
- Dependent Randomization in Parallel Binary Decision Fusion
