Joint Algorithm of Message Fragmentation and No-Wait Scheduling for Time-Sensitive Networks
Xi Jin, Member, IEEE, Changqing Xia, Member, IEEE, Nan Guan, and Peng Zeng
Abstract—Time-sensitive networks (TSNs) support not only traditional best-effort communications but also deterministic communications, which send each packet at a deterministic time so that the data transmissions of networked control systems can be precisely scheduled to guarantee hard real-time constraints.No-wait scheduling is suitable for such TSNs and generates the schedules of deterministic communications with the minimal network resources so that all of the remaining resources can be used to improve the throughput of best-effort communications.However, due to inappropriate message fragmentation, the realtime performance of no-wait scheduling algorithms is reduced.Therefore, in this paper, joint algorithms of message fragmentation and no-wait scheduling are proposed. First, a specification for the joint problem based on optimization modulo theories is proposed so that off-the-shelf solvers can be used to find optimal solutions. Second, to improve the scalability of our algorithm, the worst-case delay of messages is analyzed, and then,based on the analysis, a heuristic algorithm is proposed to construct low-delay schedules. Finally, we conduct extensive test cases to evaluate our proposed algorithms. The evaluation results indicate that, compared to existing algorithms, the proposed joint algorithm improves schedulability by up to 50%.
I. INTRODUCTION
TIME-SENSITIVE networks (TSNs) are an emerging industrial network technology based on Ethernet networks and extend a set of IEEE standards to improve the controllability of industrial networks. Thus, in addition to best-effort communications supported by Ethernet networks,TSNs also support deterministic communications that have been widely considered as an effective solution to guarantee end-to-end delay constraints in hard real-time industrial systems.
In networked control systems, TSNs have been adopted [1]–[3]. Deterministic communications contain control commands and critical sensing data, and the other data adopts best-effort communications [4]. Deterministic communications and besteffort communications have different objectives. The real-time performance of deterministic communications is the most important. Before they start to transmit, their deterministic schedules must be generated so that the transmission process can be controlled to guarantee hard real-time constraints. For best-effort communications, there is no strict constraint. Their schedules do not need to be generated in advance, and networks just try to transmit them as soon as possible. In a TSN switch,the two kinds of communications share a fixed number of output queues. Deterministic communications must be assigned dedicated queues, while best-effort communications require more queues to improve network throughput [5]. Therefore,determining how to assign and utilize the queues are the key to improving network performance.
This paper focuses on store-and-forward switching, because compared to cut-through switching, store-and-forward switching is supported by more off-the-shelf TSN products.For example, CISCO IE 4000 [6] and NXP SJA1105 [7]support only store-and-forward switching, while no off-theshelf TSN product supports only cut-through switching. In store-and-forward networks, no-wait scheduling is an effective method to make a performance trade-off between deterministic communications and best-effort communications[8]. Under no-wait scheduling, once a network switch receives a packet, it sends the packet immediately, i.e., only one queue is needed to cache the scheduled packets. Thus, when a nowait scheduling algorithm is used to generate schedules for deterministic communications, except the occupied queue, all of the other queues can be used by best-effort communications. Therefore, no-wait scheduling algorithms not only generate schedules for deterministic communications on the dedicated queue, but also improve the performance of best-effort communications.
However, when no-wait scheduling algorithms are adopted,the following issue should be considered. On the IP layer, a large message from the TCP layer must be fragmented into several smaller pieces. Each piece and its added packet header constitute a complete packet. These packets are then transmitted separately and reassembled at destination devices.In this process, fragmentation algorithms will affect the transmission delay because smaller packets have higher parallelism. For example, in Fig.1, a message of 1620 bytes must be fragmented into two pieces. In traditional Ethernet fragmentation, the length of the first packet is equal to the maximum segment size (MSS) plus a packet header, and the remaining part is contained in the second packet. Since nowait scheduling algorithms do not allow a time interval between two consecutive hops of a packet, the second packet is postponed by the first packet and cannot be transmitted earlier. In another fragmentation, to reduce the long delay, the message can be fragmented into two pieces of 810 bytes each.Although the number of packets is unchanged, the delay is reduced by approximately one-third. Message fragmentation exists in TSNs [5]. However, there is currently no work that considers message fragmentation algorithms and no-wait scheduling algorithms together. This has led to some optimizable solution spaces being ignored.

Fig.1. Effect of message fragmentation on no-wait scheduling.
Therefore, in this paper, a joint algorithm is proposed that fragments deterministic messages into packets of optimized sizes and schedules the packets under hard real-time constraints based on a no-wait strategy to improve the realtime performance of TSNs. When designing the joint algorithm, the following challenge is present. In the interest of saving resources, large packets should be used to reduce the overhead of fragmenting and reassembling. However, in the interest of temporality, a message should be fragmented into small packets, because small packets have higher parallelism and are easy to schedule. Thus, to address the above challenge, our proposed algorithms make a trade-off between these two aspects. The specific contributions are as follows.
First, a specification for the joint problem based on optimization modulo theories (OMT) is proposed. Since the joint problem is non-deterministic polynomial-time hard (NPhard), there is no polynomial time algorithm for finding optimal solutions. Thus, we formulate the problem as an OMT specification with real-time constraints to minimize the number of fragmented packets, and then invoke off-the-shelf solvers, e.g., Microsoft Z3, to solve it. Our evaluations indicate that, in an acceptable time, the OMT-based method can find optimal solutions for small networks.
Second, to improve the real-time performance of large networks, we calculate the worst-case delays of messages based on the recursive function shown in Theorem 2. Then,two corollaries are proposed on how to construct low-delay transmissions.
Third, based on the two corollaries, a joint algorithm is proposed that uses packets from large to small to construct schedules under hard real-time constraints. Thus, the proposed joint algorithm strikes a balance between saving resources and temporality. Extensive test cases were run to evaluate the joint algorithm. The evaluation results demonstrate that, compared to existing algorithms, the proposed joint algorithm improves schedulability by up to 50% and increases a small number of packets.
The rest of this paper is organized as follows: Section II reviews two categories of related work, including message fragmentation and real-time scheduling algorithms. Section III details the system model and problem. Section IV formulates the problem as an OMT specification. Section V proposes a heuristic algorithm to improve scalability of our algorithms.Section VI evaluates the proposed algorithms based on extensive test cases. Section VII concludes the paper.
II. RELATED WORK
Much research has been proposed to improve the real-time performance of industrial networks, e.g., real-time scheduling[9], resource allocation [10] and data recovery [11]. In this paper, we only focus on the real-time scheduling problem of industrial TSNs. The work in [5] formulates the basic scheduling problem of TSNs as a specification, and then uses an off-the-shelf solver to calculate schedules. Then, the work in [12] introduces the capacity limitation of TSN switches into the basic problem so that the proposed scheduling algorithms can be adopted in actual systems. Based on the above work,the work in [13] proposes a loose scheduling algorithm to transmit massive data packets using limited switch resources.In addition to the classical scheduling problem, some extended problems have been considered. The work in [14]proposes an incremental scheduling algorithm to handle dynamic data flows. The work in [15] focuses on the runtime reconfiguration of TSNs and designs a heuristic algorithm to minimize the impact of reconfiguring switches on existing data flows. The work in [16] proposes a joint routing and scheduling algorithm to guarantee the real-time performance of time-triggered communications and reduce the end-to-end delays of audio-video-bridging (AVB) communications. The work in [17] also focuses on the joint problem of routing and scheduling and evaluates extensive test cases to explore the practical limitations of the integer linear programming for TSNs. The work in [18] evaluates asynchronous scheduling algorithms in TSNs and demonstrates that asynchronous scheduling algorithms are suitable for sporadic communications. The work in [19] analyzes the worst-case delays of AVB communications based on network calculus,and then the real-time performance of AVB communications can be precisely assessed. No-wait scheduling can significantly improve system efficiency and has been widely researched in many industrial systems, e.g., energy-efficient production planning systems [20], metal-processing systems[21] and flexible manufacturing systems [22]. In [8], no-wait scheduling is introduced into TSNs. However, the objective of the above work is to minimize the total length of generated schedules. In this paper, communications have different realtime requirements, and the above work cannot be adopted.
Message fragmentation is a widely used network technology. In Ethernet networks, to reduce the message response time, the work in [23], [24] optimizes and reconfigures the maximum transmission unit size. The work in[25] designs a middleware for Ethernet networks to fragment large objects so that the worst-case delay of object-oriented transmissions can be reduced. The work in [26] evaluates four fragmentation methods based on Ethernet networks. In wireless local area networks, the work in [27], [28] designs novel fragmentation algorithms to improve the throughput of streaming videos. In the 6LoWPAN protocol, the work in[29], [30] demonstrates that packet fragmentation is beneficial to energy consumption, throughput, and end-to-end delay. In delay tolerant networks, the work in [31] fragments large data items to multiple routing paths such that routing performance can be improved. In community antenna television networks,the work in [32] considers fragmentation and scheduling together. It first schedules real-time packets and then fragments best-effort packets to make them suitable for the free slots between successive real-time packets. In timetriggered Ethernet (TTEthernet) networks, a similar method is proposed to fragment event-triggered messages to make them schedulable in idle time intervals [33]. However, the above work cannot be applied to the multi-hop no-wait scheduling problem that is addressed in this paper, and there is no work to consider the effect of message fragmentation on no-wait scheduling. Therefore, in this paper, this effect will be analyzed, and joint algorithms will be proposed to improve network performance.
III. SYSTEM MODEL AND PROBLEM STATEMENT
In this section, we will detail our system model and problem. The symbols used in this paper are summarized in Appendix.
A TSN is characterized by a two-tuple
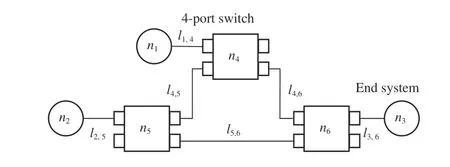
Fig.2. A time sensitive network.
In TSN switches, each egress port connects multiple queues,and each queue has a gate that can accurately control the sending of packets. Each TSN switch has a schedule table that records the precise times to open and close the gates. For example, as shown in Fig.3, at time 1, the table entry that controls port A: queue 0 is opened, and the other queues are closed. The queue with a smaller ID has lower priority. When more than one gate is opening, the packet buffered in the higher-priority queue can occupy the egress port. As described in the IEEE 802.1bQu standard, the packet in the higherpriority queue is allowed to interrupt the process of sending the packet in the lower-priority queue, and the interrupted packet will be re-assembled in the next switch. In no-wait scheduling, deterministic packets are assigned to the highestpriority queue, and the queue is always opened such that the packets will not be blocked. Although blocking packets may reduce conflicts and improve schedulability, our work still adopts no-wait scheduling for two reasons. First, no-wait scheduling is not limited by the size of the schedule table. In switch chips, the size of the schedule table is limited and fixed. Thus, switches support a limited number of gate operations. Since no-wait scheduling algorithms do not operate gates, they do not use the schedule table and do not need to consider the table size constraint. Second, under nowait scheduling, there is no schedule dissemination overhead.In a traditional network, a centralized scheduler disseminates the generated schedules to the corresponding network devices.However, under no-wait scheduling, switches forward the received packets immediately and do not need schedule information, so there is no schedule dissemination overhead.We ignore the other details of TSN switches since they have nothing to do with our proposed algorithms. Earlier works[13], [34] can help readers understand TSN switches in details.
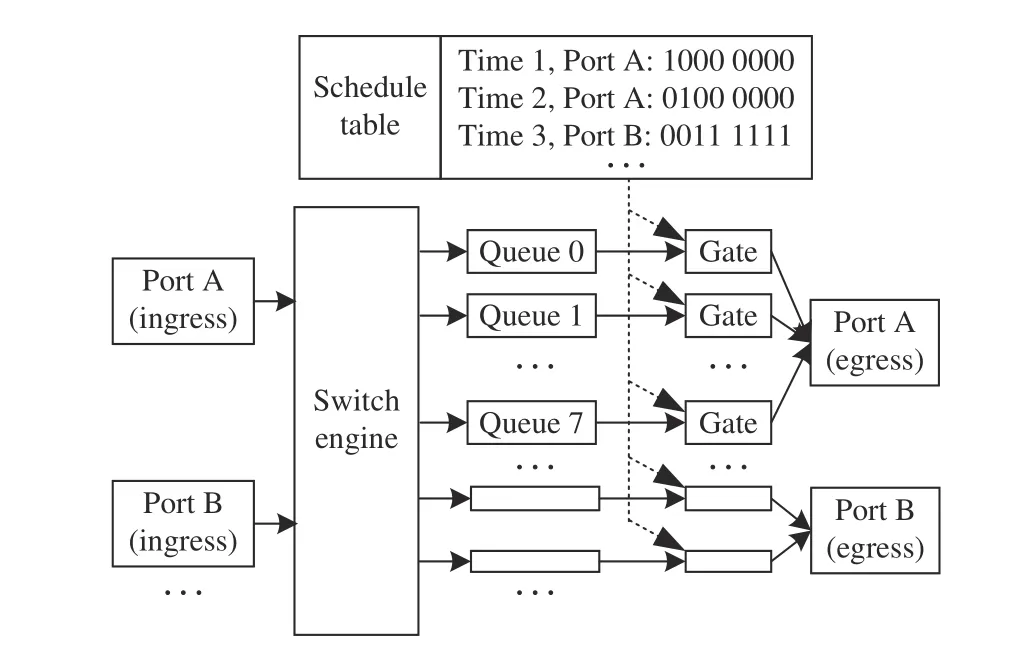
Fig.3. Architecture of a TSN switch.
Transmitting methods are designed herein only for deterministic flows. Best-effort flows are delivered by the classical best-effort services. In the following, if no specific description is given, flows refer to deterministic flows. A flow in the flow set F is characterized by a four-tuple
From Fig.1, it can be seen that message fragmentation based on the fixed MSS is not suitable for improving real-time performance. To address this problem, first, the sizes of deterministic packets are changed based on the requirements of no-wait scheduling, and then the packets are injected at a specified time that is determined by the proposed real-time scheduling algorithm. However, the number of deterministic packets significantly affects network performance because the fragmented deterministic packets not only introduce extra packet headers but also interrupt best-effort packets.Therefore, given a network and a flow set, our proposed joint algorithm of message fragmentation and scheduling is to minimize the number of packets such that the following two requirements can be satisfied.
1) Real-Time Requirement: All messages must be delivered to destinations before their absolute deadlines.
2) No-Conflict Requirement: A unidirectional link cannot serve more than one packet at the same time.
A flow set is called schedulable if it has a feasible schedule that meets all the requirements. A solution is called optimal if there are no other solutions with better objective values. When only linear networks are considered, and messages are too small to be fragmented, our problem is the same as the scheduling problem studied in [37]. Since the problem in [37]is NP-hard, our problem is also NP-hard. Therefore, to solve the problem, we propose two methods as shown in Fig.4.First, the problem is formulated as an OMT specification [38](in Section IV). Thus, if there exists a feasible solution, OMT solvers can find it. However, for some complex networks, the solvers cannot find any feasible solution in an acceptable time.Then, to improve the scalability of our algorithms, a heuristic algorithm is proposed (in Section V).
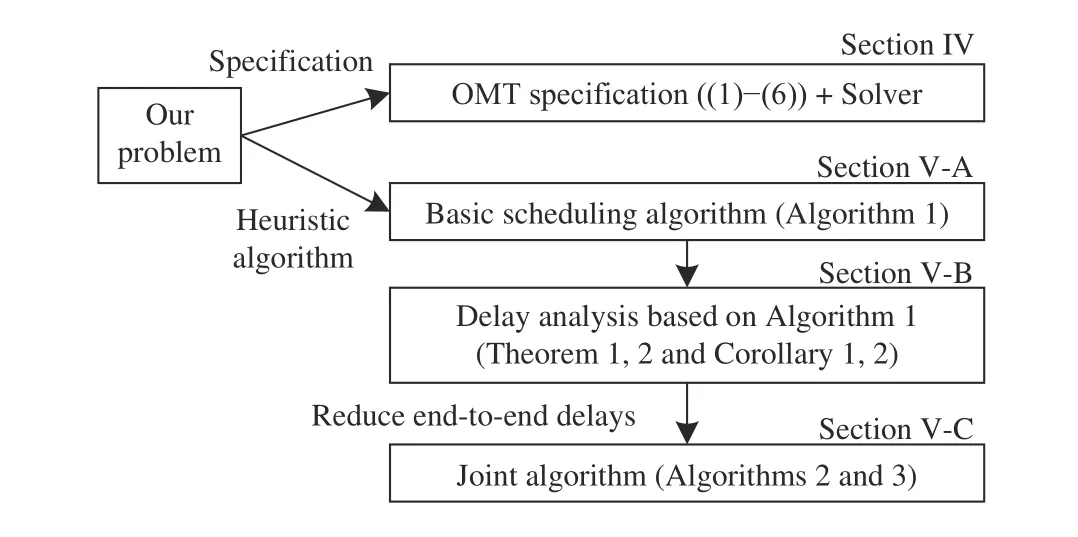
Fig.4. Overview.
IV. OMT SPECIFICATION
Satisfiability modulo theories (SMT) have been widely used to determine whether a specification is satisfiable or not [39].An OMT is an extension of a SMT and allows finding an optimal objective based on a SMT specification.
The inputs of the problem are network N and flow set F. To formulate the problem, we assume that a message is fragmented into, at most, U packets, which are denoted as{τi,j,1,τi,j,2,...,τi,j,U}. U is given by users. Three decision variables wi,j,g, si,j,gand ui,j,gare introduced. wi,j,gdenotes the injection time of packet τi,j,g. The size of packet τi,j,gis si,j,gbytes. If si,j,g=0 , τi,j,gis defined as invalid; otherwise, it is valid. The objective of this work is to minimize the number of valid packets. To calculate the number of valid packets, we use ui,j,gto denote whether a packet is valid or not. If τi,j,gis valid, i.e., si,j,g>0, then ui,j,g=1; otherwise, ui,j,g=0. Thus,the objective function is
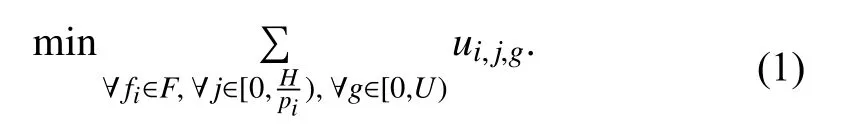
The minimizing problem respects the following constraints.
1) Range Constraint: The ranges of the variables used in the proposed model are the following:

If the size of a packet is greater than MS S, the packet has to be fragmented again on the IP layer. Thus, the upper bound of the packet size is MS S. The injection time of a packet must be between its generation time and deadline. To reduce the search space, we specify the order of packets: the packets are injected in increasing order of ID, and valid packets have smaller IDs than invalid packets.
2) Size Constraint: A message is fragmented into several packets, and the sum of the size of these packets is equal to the size of the message. For each packet, based on the definition of ui,j,g, if the size of the packet is 0, the corresponding ui,j,gis also 0; otherwise, it is 1. The size constraints are as follows:
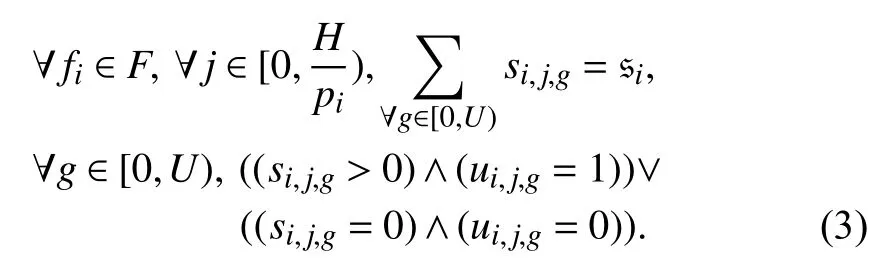
3) Real-Time Constraint: If a packet is invalid, i.e., ¬ui,j,gis true, its real-time constraints do not need to be considered;otherwise, its arrival time cannot be later than its deadline.The arrival time of a packet is equal to the injection time plus the transmission time ((si,j,g+e)/v×ri), where e is the size of a packet header. Thus, the real-time constraints are as follows:
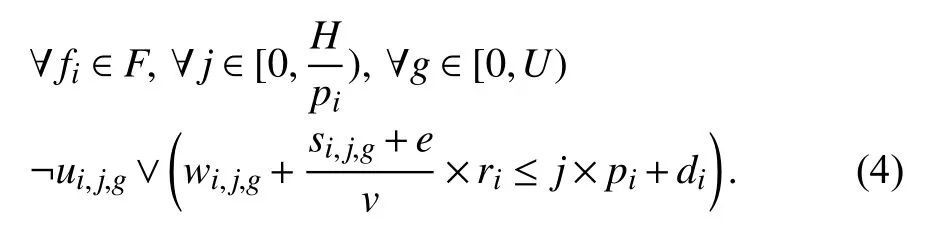
4) No-Conflict Constraint: For any two packets, under the following three conditions, we do not need to consider the conflict between them. First, the two packets are the same packet, i.e., for τi,j,gand τx,y,z, (i=x)∧(j=y)∧(g=z) is true.Second, not both packets are valid, i.e., ¬ui,j,g∨¬ux,y,zis true.Third, the two packets do not pass through the same directed link, i.e., (la,b∉Πi)∨(la,b∉Πx) is true. If the two packets do not satisfy any of the above conditions, the time intervals when they occupy the same link cannot overlap; otherwise,they conflict with each other. The constraints are as follows:

where Ai,j,g(la,b) denotes the time of starting to transmit the packet on link la,b, i.e.,

where qi,a,bdenotes that la,bis the qi,a,b-th hop in path Πi.Then, Ai,j,g(la,b)+(si,j,g+e)/v is the finish time of the packet on link la,b.
OMT solvers can find the solution of the above specification. However, for complex problems, the execution time of off-the-shelf solvers is unacceptable. Therefore, in the next section, a fast algorithm is proposed to solve the problem.
V. PROPOSED ALGORITHM
Our algorithms schedule messages based on fixed priority scheduling [40], which is effective and has been widely used in real-time systems. Under fixed-priority scheduling, each message has an unique priority, and all the messages are scheduled in decreasing order of their priorities. For easy understanding, first, in Section V-A, we assume that priorities and message fragmentation have been determined. Based on the precondition, a basic fixed-priority scheduling algorithm(Algorithm 1) can calculate the injection times for all packets.Then, in Section V-B, based on the basic scheduling algorithm, the worst-case delays of messages are analyzed in order to determine what strategy can improve the real-time performance. Finally, in Section V-C, based on the analysis,our joint algorithm to fragment messages and schedule packets is proposed (as shown in Algorithm 3).
A. Basic Scheduling
To find the main factors that affect transmission delay, how packets are scheduled is presented in this section.
Algorithm 1 is used to calculate the injection time for each packet. Each message mi,jhas a priority ρi,j. If ρi,j<ρx,y, then the scheduling algorithm calculates the injection time wi,j,gof the packets belonging to message mi,jfirst. Note that in Algorithm 1 it is assumed that all priorities ρi,jand message fragmentation {τi,j,1,τi,j,2,...} have been obtained. The method of obtaining these is introduced in Section V-C.

Algorithm 1 Initial scheduling algorithm Input: , F, , , ∀wi,j,g
Γ contains all of the unscheduled messages (Lines 1 and 4).In each iteration (Lines 2–10), Algorithm 1 calculates the injection time of the highest-priority message in Γ until there are no unscheduled messages. For message mi,j, the set Mi,jincludes all of its valid packets. The packets in Mi,jare assigned injection times (Lines 5–8) separately. If at time t a packet can be scheduled without conflict (the function NoCon flict() in Line 7), its injection time is t (Line 8). The function NoCon flict(t,τi,j,g) returns true if, when τi,j,gis injected into the network at time t, there is no conflict between τi,j,gand the other scheduled packets.

B. Delay Analysis
The end-to-end delay of a message is defined as the time duration between its generation time and its received time. In the following, analyzing the end-to-end delay of the message mi,jis considered. Based on Algorithm 1, it is known that the messages in the conflict set Ω(mi,j) (Definition 1) determine the delay of mi,j. When all the messages of Ω(mi,j) are transmitted in the active interval of mi,jand before the transmissions of mi,j, the worst-case delay of mi,joccurs.S(mi,j) is used to denote the packets that belong to the messages of Ω(mi,j), and S(mi,j)={τa,b,g|∀τa,b,g∈Ma,b,∀ma,b∈Ω(mi,j)}.
Definition 1: Ω(mi,j) includes all of the messages ma,bthat satisfy the following conditions:
1) ma,bhas a higher priority than mi,j, i.e., ρa,b<ρi,j.
2) ma,band mi,juse the same links, i.e., Πa∩Πi≠∅.
3) the active intervals of ma,band mi,joverlap each other,i.e., [b×pa,b×pa+da)∩[j×pi,j×pi+di)≠∅.
Based on Definition 1, it is known that the higher-priority messages in Ω(mi,j) pass through the links of Πi, but maybe not all of them. However, as long as one of the hops of mi,jis delayed by the higher-priority messages, the entire mi,jis delayed. This is the same as transmitting higher-priority messages over the entire path. Hence, to bound the worst case,all of the higher-priority messages are extended to the entire path Πi, i.e., when the delay of mi,jis considered, the routing path of a higher-priority message ma,bis also Πi. This path extension does not result in an overestimation of the worst case or an underestimation of the conflicts from the higherpriority messages (as shown in Theorem 1). Intuitively,changing the path will cause more delay, or some conflicts may be neglected. However, in Theorem 1, we proved that the above situations do not exist.
Theorem 1: In the proposed model, the path extension for the messages in set Ω(mi,j) does not exacerbate the worst-case delay and does not lose the conflicts from the higher-priority messages.
Proof: First, the worst case is discussed. The path extension does not allow messages to be transmitted in parallel since all of them occupy the same links. Owing to the conflicts introduced by other messages, when the delay of mi,jis analyzed, the start times of the higher-priority messages inΩ(mi,j) are unknown and can be any time. Thus, even though the paths are not extended, it is possible that the transmission times of the messages in Ω(mi,j) do not overlap each other,i.e., they are serial. Therefore, the path extension does not exacerbate the worst case.

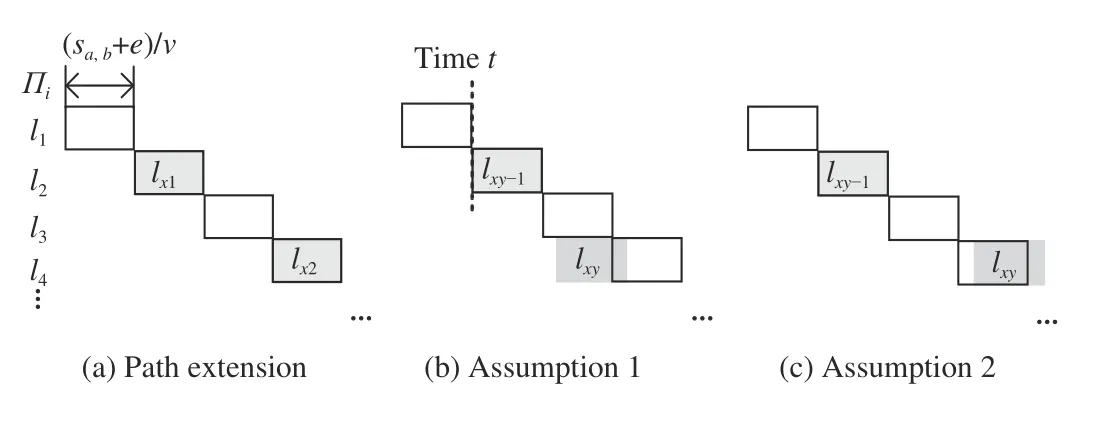
Fig.5. Illustration of higher-priority message ma,b.

Theorem 2: The generation time of mi,jis set to time 0, and the worst-case delay of mi,jis equal to the relative finish time of the last packet τσ+ςbounded by a recursive function

where

and

Proof: The finish time of a packet is equal to the finish time of its previous packet plus its own delay δ.
First, the calculation in the subset {τ1,...,τσ} is explained.For the first packet τ1, its finish time is equal to its transmission time (see (8)). Then, for packet τk(2 ≤k ≤σ),the following two conditions correspond to the first two lines of δ(τk).
Condition 1: k ≤σ and sk≤sk−1. If there is no other conflict outside Πi, τkshould be transmitted after τk−1in succession (as shown in Fig.6(a)). However, some external factors, such as the path outside Πiand the unknown relationship between the generation time of τkand transmission time of τk−1, may make τkmore delayed. This additional delay is called a gap (as shown in Fig.6(b)). When the gap length is less than (sk+e)/v, the time duration of τkoccupying l2overlaps the time duration of τk−1occupying l3.Thus, between τkand τk−1, no packet can be transmitted continuously on l2and l3. The gap can only be idle. In the worst case, the gap length is ((sk+e)/v)−ε, where ε approaches 0. If the gap length is greater ((sk+e)/v)−ε, then l2and l3can be used continuously, and a subsequent packet can be inserted. Although it is possible that due to the delays introduced by external factors the subsequent packets in S→(mi,j) cannot be inserted, the packets of mi,jcan be inserted because they do not have the path outside Πi. Therefore, the delay of δ(τk) is its transmission delay plus the worst-case gap.

Fig.6. Illustration of Condition 1.
Condition 2: k ≤σ and sk>sk−1. If the two packets can be transmitted in succession, the finish time of τkshould be Finish(τk−1)+ri×(sk+e)/v−(ri−1)×(sk−1+e)/v (as shown in Fig.7(a)). However, due to unknown conflict, there may be a gap (sk−1+e)/v−ε between the two packets (as shown in Fig.7(b)). Hence, the finish time of τkis


Fig.7. Illustration of Condition 2.
In Theorem 2, the impact of fragmentation and scheduling on the worst-case delay is formulated. Based on the theorem,we can prove Corollary 1 and Corollary 2. Then, the worstcase delay can be reduced by constructing a proper solution based on the two corollaries.
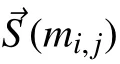
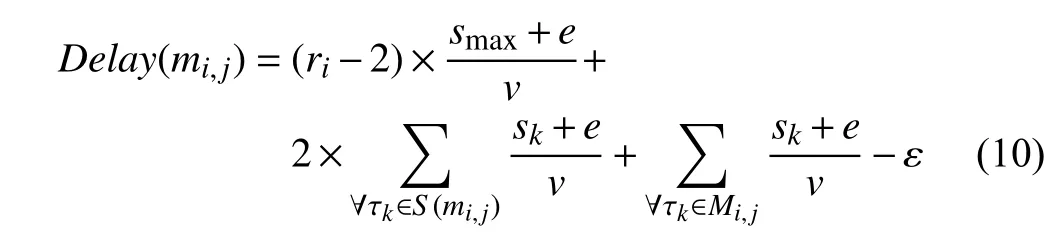

Proof: First, we discuss S(mi,j) and Mi,j, respectively, and then consider the relationship between them.




Algorithm 3 Joint algorithm Input: F, ∀Mi,j∀wi,j,g∆Output: , →Ω=PriorityAssignment(F)1: ;2: = MSS; ;¯sk=1 k ≤|→Ω|3: while do 4: fragment the -th message, denoted , into multiple packets of bytes;mi,j¯s k 5: for each do t=(j×pi) (j×pi+di −si,j,g+e τi,j,g ∈Mi,j 6: for to do NoConflict(t,τi,j,g)v ×ri)7: if then wi,j,g=t 8: ; break;∃τi,j,g ∈Mi,j 9: if is not scheduled then kΩ(mi,j)10: = the smallest ID in ;∀g ∈[k,|→Ω|]g 11: , clear the injection times of the -th message; //*schedules roll back*//¯s−=∆12: ;¯s<λ 13: if then 14: return FAIL;15: else k++16: ;∀Mi,j∀wi,j,g 17: return , ;

VI. EVALUATION
In this section, we evaluate the proposed algorithms based on extensive test cases. Three metrics are used in our evaluation: 1) schedulable ratio is the percentage of test cases for which an algorithm can find a feasible solution; 2) the number of packets is our objective as shown in 1); and 3)execution time is the time required to generate a feasible solution.
The proposed joint algorithm (JA) and OMT-based method are compared with the following five methods: ME, ME+AD,ME+EN, JA-EN and BL.
1) ME adopts the traditional Ethernet fragmentation and the earliest deadline first (EDF) scheduling algorithm [40].
2) ME+AD is an extension of ME. If ME cannot schedule a test case under the initial MSS, ME+AD decreases the MSS by the same parameter ∆ as JA and re-schedules the test case.Repeat this process until the test case can be scheduled.
3) ME+EN is also an extension of ME. The only difference between ME+EN and ME is that ME+EN enlarges the last packets of messages, while ME does not.
4) JA-EN is the same as JA except that it does not enlarge the last packets.
5) BL is a baseline for comparisons. To illustrate the efficiency of JA, an optimal result is needed. However, in an acceptable time, off-the-shelf solvers can only find optimal results for simple problems. Thus, when optimal results cannot be found, an approximately optimal result is needed,which is BL in our evaluations. When a schedulable ratio is considered, BL is defined as the percentage of test cases that satisfy the following necessary condition: if all port utilizations are not larger than 100%, the test case is schedulable. When the comparison metric is the number of packets, BL is the sum of packets that are fragmented by the traditional Ethernet fragmentation. Thus, BL is better than or equal to the optimal result. If the proposed algorithm is close to BL, it must be close to the optimal results.
All algorithms are written in C and run on a Windows machine with a 2.5 GHz CPU and 8 GB of memory.
All test cases are generated based on the parameters shown in Table I. Each test case includes n/2 switches and n/2 end systems. Each switch has 4 ports, one of which is connected to an end system, and the remaining ports can be connected to other switches. The switch-end system pairs are randomly located on a two-dimensional coordinate system. Then, the switches are traversed in increasing order of ID. For each switch, the free ports are connected to the nearest switches that still have free ports. To illustrate the universality of our algorithms, we do not limit the network topology. There are f flows. The flows randomly select their source and destination end systems. Routing paths are generated using the Dijkstra algorithm. To restrict the length of the hyperperiod, we adopt harmonic periods. Each period is a random number that is in the period range p and conforms to the expression 400 μs×2n,where n is a non-negative integer. Message sizes are random numbers in the message size range s. The deadline of a flow is also a random number in the range [pi/2,pi]. The transmission speed v=31 bytes/μs is measured in our simple prototype network such that the logical time of test cases can be mapped to the physical time. In the following comparisons, these parameters are changed and extensive test cases are generated to evaluate the efficiency and universality of the proposedalgorithm. In Section VI-A, we compare OMT with JA, ME and BL. Then, due to the long execution time of the OMT solver, in Section VI-B, except OMT, the other algorithms are fully evaluated.

TABLE I PARAMETERS
A. Evaluations With OMT
The Microsoft solver Z3 [43] is invoked to solve the OMT specification. The time limit of Z3 is set as 600 s. To make test cases solvable, n=4 , f =4, and p={400 μs,800 μs} are set. The other parameters are shown in Fig.9 . For each parameter setting, 200 test cases are generated. Figs. 9 (a) and 9(b) show schedulable ratios and the number of packets normalized with BL, respectively. Since ME adopts traditional fragmentation, it does not introduce extra packets. However,the traditional algorithm has the worst schedulable ratio. OMT is not better than JA because Z3 cannot find optimal results for some test cases within the time limit. The schedulable ratio of JA is close to BL. This illustrates that JA can significantly improve the schedulability. Other than OMT, the other algorithms can finish execution within 10 ms. The execution time of OMT is shown in Fig.10. Most of the test cases can be solved by Z3 in 300 s. Once the execution time exceeds 300 s, it is difficult to solve these test cases in 600 s. The test cases in Fig.10 (b) have short execution times because they include the minimum number of packets, i.e., the minimum number of variables. Therefore, if a problem includes a small number of variables, OMT can be adopted to find optimal results; otherwise, JA is the best choice.

Fig.10. Execution time of OMT.
B. Evaluations Without OMT
To fully evaluate the proposed algorithm, in the following,each parameter is changed over a larger range to generate test cases. The basic setting is shown in the caption of Fig.11.Then, Figs. 12–15 change the period parameter, size parameter, step value, and number of flows, respectively, to illustrate the efficiency and universality of JA. For each parameter setting, 2000 test cases are generated.
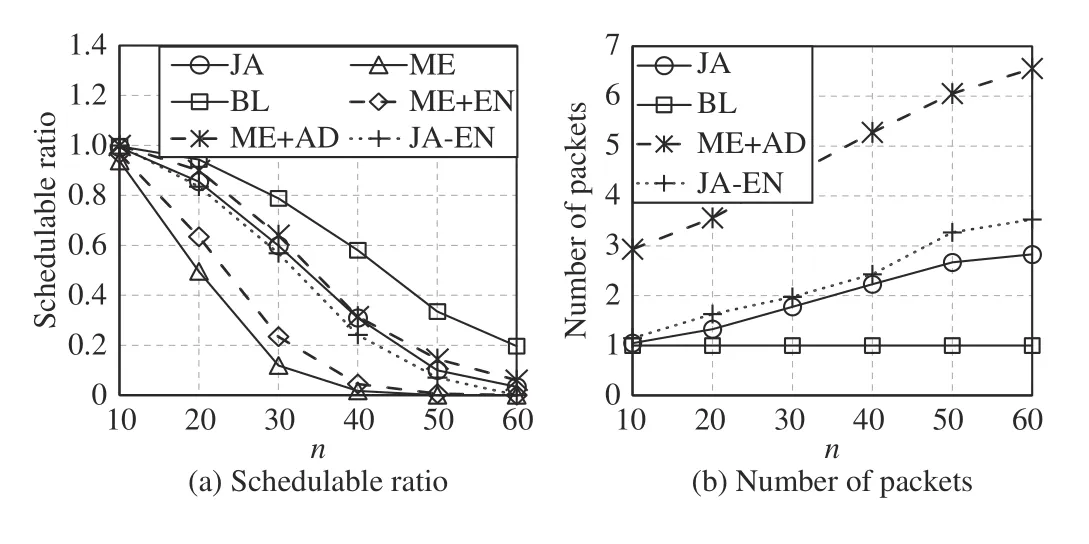
Fig.11. Comparisons under varying n, p=[800 μs,6.4 ms] , s=[1461,5480],∆=146, and f =n.
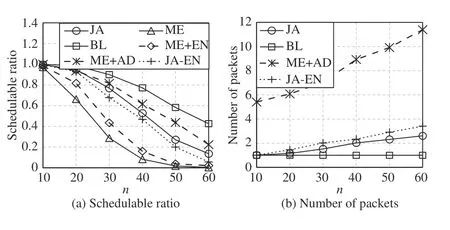
Fig.12. Comparisons under varying n, p=[800 μs,12.8 ms], s=[1461,5480], ∆=146, and f =n.
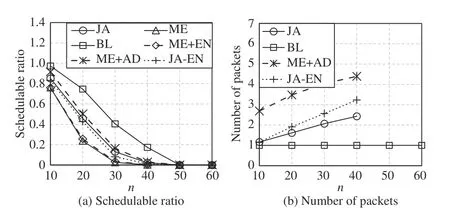
Fig.13. Comparisons under varying n, p=[800 μss,6.4 ms], s=[1461,8760], ∆=146, and f =n.

Fig.14. Comparisons under varying n, p=[800 μs,6.4 ms], s=[1461,5480], ∆=438, and f =n.
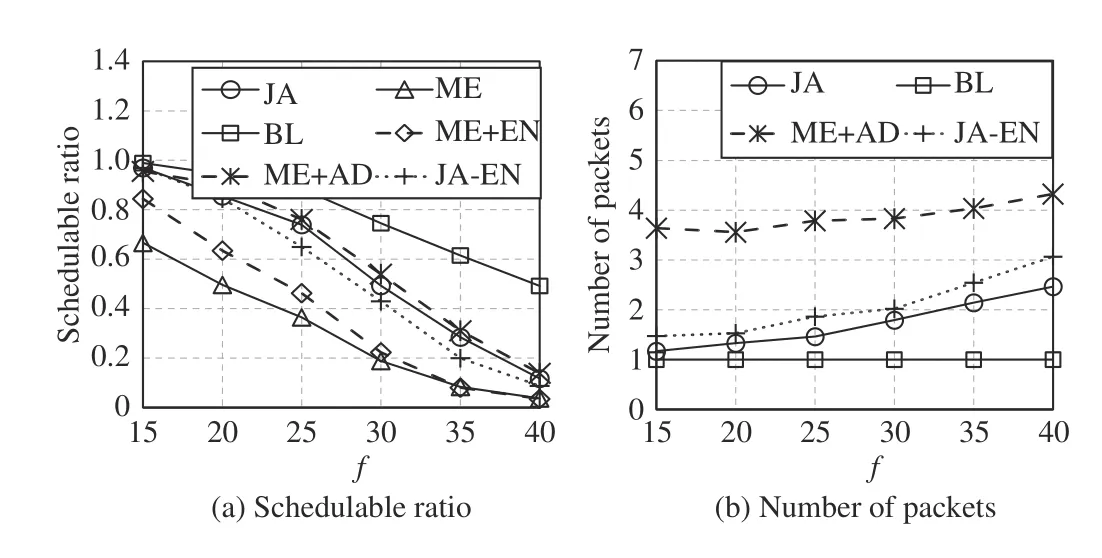
Fig.15. Comparison under varying , p=[800 μs,6.4 ms], s=[1461,5480], ∆=146, and n=20.
Fig.11 shows the comparison with a varying the number of network nodes. The schedulable ratio decreases as the number of nodes increases. This is because the greater the number of nodes, the more difficult the scheduling becomes. ME+EN is better than ME. This is because ME makes more resource fragmentations unusable and cannot provide a long enough time duration to transmit no-wait packets. Fig.11 (b) shows the number of packets normalized with BL. ME and ME+EN are not shown since they both adopt the traditional fragmentation and have the same number of packets with BL.The larger the network, the longer the routing path. Thus,when n=60, to make flows schedulable, smaller packets are needed to improve the parallelism such that the delay introduced by the long path can be reduced. Therefore, the number of packets increases as n increases. Compared to ME,although JA introduces more packets, it still can find feasible solutions. This is because, in ME, different packet sizes cause excessive resource fragmentations. ME+AD uses many small packets to improve the parallelism. Thus, the schedulable ratio of ME+AD is slightly better than JA, but the number of packets of ME+AD is more than double that of JA. Therefore,in a network, if there are sufficient resources, the smaller MSS should be adopted to improve the real-time performance.Compared to JA, JA-EN causes more resource fragmentations. Hence, even though part of messages are fragmented into smaller packets to improve the parallelism,the schedulable ratio of JA-EN is still less than that of JA.
The period range is extended to illustrate its effect on schedulable ratios and the number of packets, as shown in Fig.12. Compared to Fig.11(a), Fig.12(a) shows higher schedulable ratios because more time resources can be utilized to make flows satisfy real-time constraints. Then, since the real-time constraints are easily satisfied, messages do not need to be fragmented into small packets to reduce the delay. Thus,in Fig.12(b), the number of packets of JA is less than that in Fig.11(b). ME+AD makes full use of the time resources to improve the schedulability but results in too many packets.Compared to ME+AD, JA not only guarantees the requirements of deterministic communications but also reserves more resources for best-effort communications.
In Fig.13, the message size is larger than that of other figures. Since large messages are difficult to schedule, the schedulable ratios in Fig.13(a) are low. Compared to JA,although ME+AD improves the schedulable ratio by 3%, it consumes more than twice the resources. JA-EN is close to JA because large messages can be fragmented into more packets so that JA-EN searchs fesabile solutions in a larger solution space. When n ≥50, no algorithm can schedule test cases, not even BL. Therefore, in real applications, the periods and deadlines of large messages must be extended to make them schedulable, as illustrated in Fig.12.
In Fig.14, ∆ is increased. Messages cannot be fragmented into small pieces. Both the schedulable ratio and the number of packets are reduced. Other than ∆, if the other parameters are changed, test cases are changed accordingly. Only ∆ is independent of test cases. Therefore, when given a real network, we can adjust ∆ to trade off between the schedulable ratio and the number of packets.
Fig.15 shows the comparison under varying f. As f increases, the increased packets make more test cases unschedulable, and thus the schedulable ratio decreases. The number of packets increases slowly, because the test cases that contain more packets are unschedulable, and these unschedulable test cases are not included in the figure. When there are not many flows, the schedulable ratio of ME+EN is significantly higher than that of ME. Therefore, ME+EN is an efficient method for low-load test cases.
VII. CONCLUSIONS
In this paper, to improve the real-time performance of networked control systems, the joint problem of message fragmentation and no-wait scheduling is explored. First, an OMT specification is proposed and then an off-the-shelf solver utilized to find its optimal solution. However, the OMT-based algorithm is limited by the execution time of the off-the-shelf solver. Then, to improve the scalability of our algorithm, a heuristic algorithm is proposed. The algorithm constructs low-delay fragmentation and schedules based on the message delay analysis. Finally, extensive test cases are conducted to evaluate the proposed algorithms. The results indicate that the proposed joint algorithm outperforms existing ones. In the future, we will implement a TSN switch based on FPGA and evaluate our algorithms in a real TSN.

APPENDIX SYMBOL
 IEEE/CAA Journal of Automatica Sinica2021年2期
IEEE/CAA Journal of Automatica Sinica2021年2期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- Digital Twin for Human-Robot Interactive Welding and Welder Behavior Analysis
- Dependent Randomization in Parallel Binary Decision Fusion
- Visual Object Tracking and Servoing Control of a Nano-Scale Quadrotor: System, Algorithms,and Experiments
- Physical Safety and Cyber Security Analysis of Multi-Agent Systems:A Survey of Recent Advances
- A Survey of Evolutionary Algorithms for Multi-Objective Optimization Problems With Irregular Pareto Fronts
- A Survey on Smart Agriculture: Development Modes, Technologies, and Security and Privacy Challenges
