基于改进Canny算子的双水平集医学图像分割
李祥健,朱家明,徐婷宜
(扬州大学 信息工程学院,江苏 扬州 225127)
0 引言
自20世纪70年代开始,图像分割得到了广大学者的重视,提出了上百种的分割方法,大致可以分为基于边缘的分割方法、基于区域的分割方法、基于能量泛函的方法、基于特定理论的方法[1]。水平集方法在1988年首次被提出来,用于解决流体力学的问题,它将一个二维演化曲线嵌入到一个三维空间函数中,通过求解这个空间函数的极小值得到最终的演化结果[2]。后来有学者在此基础上改进了水平集模型,克服了基于边界水平集模型容易发生边界泄露、对初始条件苛刻的缺点。
CV模型的提出后,受到了学者的广泛关注。传统的水平集由于图像的离散性以及外界噪声的影响,经过一段时间演化后会逐渐失去光滑性并出现尖角,因此需要周期性地重新初始化函数。为了解决这个问题,文献[3]提出在水平集函数中加入能量惩罚项,缩短了水平集演化时间。医学图像中往往包含多个目标区域,传统的单相水平集无法分割,文献[4]提出多相水平集的方法,用N个水平集函数表示2N个相,但是MRI图像往往存在灰度不均匀的现象,直接运用多相水平集模型进行分割,很难得到理想的分割结果。因此Wells等人在水平集模型中加入了偏移场矫正,可以较为准确地分割医学图像,但算法计算量大,运行时间较长。
医学图像存在灰度不均匀和边界复杂的问题,传统的双水平集模型无法达到理想的分割效果,因此本文将Canny算子与水平集模型相结合,首先在Canny算子的基础上加入梯度模板,用来解决传统Canny算子无法完全检测出复杂图像边缘的问题;然后将检测后的图像融入到双水平集模型中,通过在水平集模型中加入偏移场来解决灰度不均匀的问题,实验证明,本文模型既提高了分割的精度,又缩短了分割时间。
1 Canny算子
1.1 传统的Canny算子
Canny算子边缘检测根据图像梯度变化进行检测[5],将有用的信息从中提取出来。Canny算子在处理图像边缘信息时的精确度较高,是一种标准的多级检测算法,在实际应用中较为广泛。Canny算子一般包括高斯滤波、计算梯度强度和方向、非极大值抑制以及阈值算法检测和连接边缘四个步骤。
高斯滤波主要作用是去除噪声,一般噪声都是集中于高频信号,在分割时会被误认为是图像边缘,所以首先要减少噪声,才能提高分割时的精确度。图像中的边缘会指向不同的方向,所以需要采用不同的方向模板,以保证检测的准确性,一般采用水平和垂直两个方向模板。经过模板检测后图像的梯度边缘具有多个像素宽,为得到清晰的梯度图,通常采用非极大值抑制的方法,将最大的梯度保留下来。最后,通过双阈值消除噪声和颜色变化引起的小梯度值。
1.2 改进的Canny算子
传统的Canny算子在计算梯度强度和方向时,一般只从水平和垂直两个方向进行检测,梯度幅值和梯度方向如下所示:
(1)
θ=arctan(Gy/Gx)。
(2)
在实际应用中图像边缘会指向不同方向,仅从水平和垂直两个方向检测,往往会检测出伪边缘,为解决这个问题,本文在此基础上增加了对45°和135°方向的检测,其梯度幅值和梯度方向如下所示:
(3)
(4)
为比较传统Canny算子与改进后Canny算子对图像边缘检测的区别,选取了脑部MRI图像,分别用两种方法对图像边缘进行检测,检测结果如图1所示。
2 水平集模型
2.1 双水平集
CV模型[6]是由MS模型演化而来,它将MS模型中的分段光滑函数用一个分段常值函数替代,可以将图像分为目标和背景两个区域,水平集的能量泛函如下所示:
(5)
式中,c1,c2分别为:
(6)
(7)
传统的CV模型对单目标和灰度均匀的图像分割效果较好,但是无法分割多目标的复杂图像。为了完成对复杂图像的分割,本文采用DCV模型即双水平集模型进行分割[7],用两条水平集函数将图像分为4个互不重叠的部分Ω1,Ω2,Ω3,Ω4,其能量泛函如下:

(8)
2.2 双肼势函数
水平集函数在演化过程中,经过一段时间后会失去光滑性,导致计算结果偏离真实情况,因此在演化过程中需要多次重新初始化水平集函数[8],造成演化过程耗时太长,为了避免这个现象,提出在水平集模型中加入能量惩罚项,采用单肼势函数作为距离规则化项,表达式如下:
(9)
(10)
式(9)是距离规则化项表达式,式(10)有唯一的极小值点x=1,由梯度下降流公式得:
(11)
式(11)是一个扩散方程,扩散率D=φdp(|∇φ|),当|∇u|趋近于0时,扩散率为负无穷大,会影响数值计算的准确性。为了解决这一问题,本文采用双肼势函数来代替单肼势函数,其表达式为:
(12)
式中,方程的扩散率为有界常数,避免了趋于无穷大的现象,提高了数值解精度。
2.3 偏移场拟合
医学图像在成像过程中,由于光照或者成像设备的原因,会导致灰度不均匀的现象[9],也就是偏移场,偏移场的产生会影响对图像病灶区域的分割,造成诊断结果的不准确性。目前普遍采用的MRI图像模型如下:
J(x)=b(x)I(x)+n(x),
(13)
式中,J(x)为观测到的图像,b(x)表示偏移场,I(x)为真实图像,n(x)表示噪声[10]。通常采用一组正交基函数来线性拟合偏移场,或者通过log转换运算将偏移场线性化[11],然后引入一个高斯核窗口函数来限定邻域区间,得到最终的能量方程为:
E=λ1∬ΩK(y-x)|J(x)-b(x)c1|2H(φ)dxdy+
λ2∬ΩK(y-x)|J(x)-b(x)c2|2(1-H(φ))dxdy。
(14)
这种模型中用分段常值来表示图像灰度,并且认为灰度的不均匀变化是一个平滑的过程,但实际中真实图像的灰度不是分段常值,而且偏移场也不是连续光滑的[12],这样会影响最终分割结果的精确度。为了解决这个问题,本文采用一个模糊隶属度函数来表示含偏移场的图像,假设图像中含有n个不同的组织,每一个组织的灰度值为一个常数,那么含偏移场的图像可以表示为:
(15)
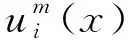
(16)
3 Canny算子与水平集模型
用Canny算子对图像进行边缘检测,将处理结果G(x,y)代替水平集算法中的原图I(x,y),并且在水平集距离规则化项中采用双肼势函数,最后加入偏移场拟合得到能量方程:
E=E(c1,c2,c3,c4,φ1,φ2)+βp(φ)+J(φ)=
(17)
式中,Mi(φ)表示图像的4个区域,其中,i=1,2,3,4。
(18)
根据Euler-Lagrange方程求解,得到水平集方程分别为:
((u0-c1)2-(u0-c3)2)Hε(φ2)-
βdiv(dp(|∇φ1|)∇φ1),
(19)
((u0-c1)2-(u0-c3)2)Hε(φ1)-
βdiv(dp(|∇φ2|)∇φ2) ,
(20)

(21)
4 实验结果与分析
本文算法流程:首先通过改进的Canny算子对图像进行边缘检测,避免了伪边缘的产生,然后在偏移场模型中加入了模糊隶属度函数,解决了灰度不均匀问题,最后将Canny算子和偏移场融入到双水平集模型中,实现了对边界复杂、灰度不均匀图像的分割。
实验环境:Matlab 2014a,Windows7,CORE i5 -3230M,CPU 2.60 GHz,4.00 GRAM。
实验参数:μ=0.001*2552,Δt=0.01,v=1,水平集函数迭代次数为50次。
为了验证本文Canny算子改进后对医学图像的分割效果,选取了图2(a)作为原始图像,其边界较为简单,图2(b)是传统Canny算子的分割效果图,图2(c)中Canny算子用自适应中值滤波替换高斯滤波[13],图2(d)是本文模型的分割效果图,从最终的分割效果图可以看出本文模型优于其他两种方法,能很好地分割出图像边缘。
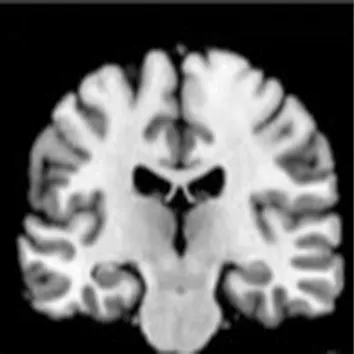
(a) 医学图像
为了验证本文模型对复杂图像分割的有效性,选取了图3(a)作为原图,分别用三种Canny算子对其进行分割,从最终分割效果图可以看出,其他两种算法会出现伪分割现象,而本文模型能准确地分割出边缘。
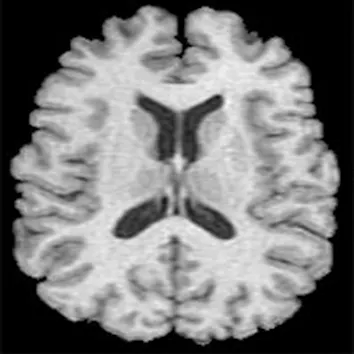
(a) 医学图像
为了验证本文模型对于灰度不均匀图像的分割效果,选取了两幅信息量不同的医学图像。图4(a)的信息量较小,通过去除偏移场之后能很好地保留原图像的信息,图4(d)的信息量较大,从效果图4(f)可以看出,去除偏移场之后仍然能够保持原图像的基本结构信息,证明了本文模型对于灰度不均匀图像能够起到很好的分割效果。

(a) 医学图像1
为了比较本文与DCV模型以及LGIF模型[14]在分割精度以及运行时间上的区别,选取了图5(a)作为原始图像,分别迭代30次之后效果图如图5(b)、(c)、(d)所示。
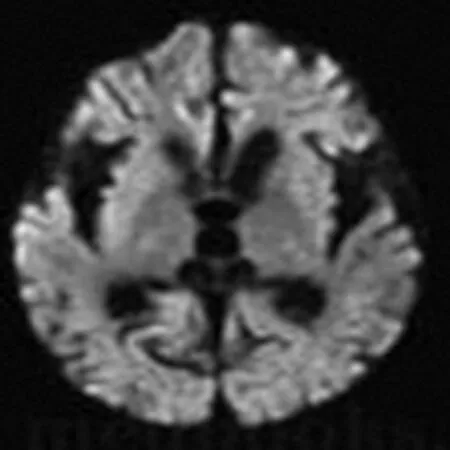
(a) 原始图像
表1记录的是分别采用DCV模型、LGIF模型和本文模型迭代30次所需要的时间,可以看出本文模型运行速度要快于其他两种模型。

表1 3种不同模型运行时间比较Tab.1 Comparison of running time of three different models
为了更加科学直观地比较三种方法对医学图像的分割效果,本文采用JS指标[15]对分割结果进行分析:
(22)
JS的值决定分割结果的好坏,值越大说明算法的分割效果越好。3种不同算法的JS指标如表2所示,可以看出本文模型可以更好地获取原图像的信息,并且双肼势函数的加入提高了函数数值解的精度,使得曲线演化更加准确,分割的时间也大大缩短。

表2 3种算法分割的JS值Tab.2 JS values divided by three algorithms
5 结束语
针对医学图像中灰度不均匀、边界复杂的问题,本文在Canny算子的基础上加入45°和135°方向上的梯度模板,解决了传统Canny算子检测时出现伪边缘的问题,提高了对于复杂边界图像的检测能力,在偏移场模型中加入模糊隶属度函数,提高了分割的准确度,最后在距离规则化项中使用双肼势函数,提高了图像的分割效率。实验结果表明,本文模型相比于DCV模型以及LGIF模型,在分割速度上更快,而且对于图像的分割精度也更高。

