四维直接序列扩频调制技术识别方法
华 博,毛忠阳,康家方,刘传辉,张 磊
(海军航空大学 战勤学院航空通信教研室,山东 烟台 264001)
0 引言
随着通信技术的发展,新型调制技术不断涌现,新旧调制技术的共存不可避免,而调制方式的不可识别将会导致通信双方无法快速有效地进行信息传递和沟通,这一问题在无线通信中最为突出。因此,通过一定技术手段对调制信号进行处理,并从中提取有用信息,实现对不同调制信号的识别,从而采取相应的解调算法,是解决不同通信体制互不识别的一个研究重点。作为一种新型扩频调制技术,四维直接序列扩频(Four Dimensional Direct Sequence Spread Spectrum,4D-DSSS)调制信号与传统直接序列扩频调制信号究竟有哪些不同?是否能够从中挖掘出可用于信号调制体制识别的特征参量,从而实现不同调试方式之间的互联互通?目前未见相关研究报道。
4D-DSSS调制技术[1-2]是一种新型扩频调制技术,该技术基于单一扩频码,将Hilbert变换技术与正交双通道传输相结合,在不扩展系统传输带宽的前提下,扩展直接序列扩频(DSSS)调制的空间维度,以此提高扩频通信的传输效率,增大通信容量。相比于传统DSSS技术,4D-DSSS具有传输速率高、频带利用率高及通信容量大等优点,在短波通信、超短波通信以及卫星导航等领域具有更广阔的应用前景[3]。因此,本节将结合调制信号自动识别方法,研究4D-DSSS技术体制与传统扩频技术体制之间的联系与区别,探索新旧扩频技术的结合方式,并进行向下可识别的技术设计研究,在物理信号层实现多维直接序列扩频调制技术体制的可识别性。
1 时频特征提取
4D-DSSS调制技术有巨大的应用潜力,但由于该技术采用新型的调制解调方式,无法与传统DSSS调制的系统直接互通。因此,为了避免在两种扩频调制体制同时存在的情况下设备无法互联互通,采用4D-DSSS调制的新设备必须可识别传统DSSS调制,在接收时,必须能够正确识别信号的调制方式。调制方式识别是一种典型的模式识别问题,识别流程如图1所示。

图1 调制信号识别流程Fig.1 Modulation signal recognition process
信号预处理部分的主要功能是通过对接收信号下变频等预处理,得到满足后续处理要求的数据;特征提取部分是利用不同的分析工具实现对调制信号的特征提取,主要包括时频分布特性[4-5]、小波特性[6-7]以及高阶累计量特性[8-12]等;分类识别部分主要是利用决策树、神经网络[13-16]等分类器实现对不同特征参数的分类,以达到精确识别的目的。
时频特征包括信号的时频域特征和时频分布特征,而已调信号总是在幅度、相位以及频率上表现出调制方式的特征[17],因此,可以提取信号时域特征实现对信号调制方式的识别。在某些情况下,从时域上提取的特征不足以对调制方式进行分别,而在频域却区别明显,因此,可将信号进行傅里叶变换再提取特征,从而取得更好的识别率。本着循序渐进的研究思路,首先从调制信号的时频域特征出发,分析DSSS调制信号与4D-DSSS调制的时频域特性。
4D-DSSS调制信号比传统DSSS调制信号多两个维度,因此,在相同传输带宽的条件下,4D-DSSS调制信号的幅值比DSSS调制信号高,其时域波形与功率谱密度如图2所示。
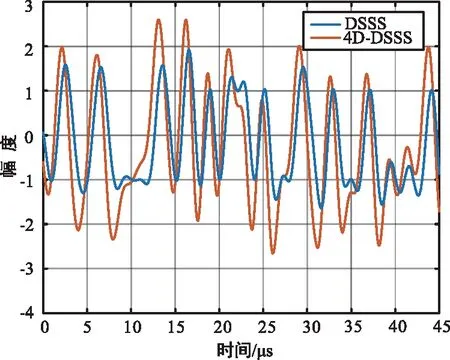
(a) 调制信号时域波形
由图2(a)可知,相比于传统直扩信号,四维直扩信号的幅度更高,这是由于4D-DSSS调制信号由多路信号叠加而成,但由于噪声的影响,仅利用信号的时域波形不足以完成调制信号的识别。由图2(b)可知,4D-DSSS信号与DSSS信号的主瓣带宽相同,旁瓣功率同时衰减约-30 dB。从上述分析可知,两种调制信号的时频域特征并不明显,因此,需要进一步提取时频域特征,以实现调制信号的辨识。
经接收机下变频和采样处理后的信息序列s(n),其瞬时幅度为每个采样点的模,即an(i)=|s(n)|,则信号的绝对幅度标准差为:
(1)
式(1)反映了信号的绝对幅度变化信息,该特征可以区分不具有归一化绝对幅度信息的调制方式,一般情况下δaa需要与信号幅度谱峰值结合使用。信号幅度谱峰值,也称为信号归一化瞬时幅度功率谱密度最大值,可以将其表示为:
(2)
式中,N为样点数,an(i)为信号瞬时幅度,acn(i)为中心归一化瞬时幅度:
(3)
式中,E(a(i))为瞬时幅度的平均值,利用归一化的瞬时幅度提取信号特征可以降低信道噪声的影响。式(2)反映了信号瞬时幅度的波动情况,对于包络随时间变化的信号,其γmax理论值大于零。两种调制信号的幅度谱峰值和绝对幅度标准差如图3所示。
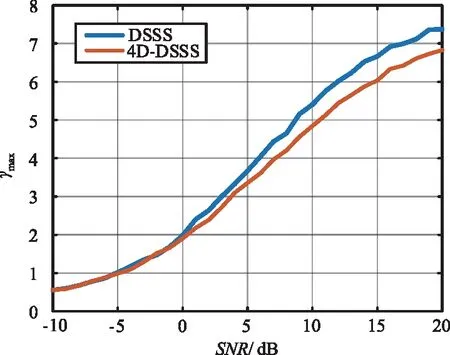
(a) 调制信号幅度谱峰值
由图3可知,当SNR<0 dB时,两种调制信号的幅度谱峰值具有一定的可区分性,而绝对幅度标准差只有在SNR<5 dB时,才能区分两种调制信号。因此,幅度谱峰值和绝对值标准差只有在大信噪比的条件下,才具有识别两种调制信号的能力,难以满足实际可识别性要求。
调制信号的时频分布特征是将信号特征提取从单一维度扩展到二维时频域,通过提取信号时间和频率的联合变化特征实现对不同信号的识别。不同的时频分析方法所提取信号特征也不尽相同,目前被广泛应用的是短时傅里叶变换 (Short Time Fourier transform,STFT)[18],通过选取适当长度的信号分析窗滑动截取信号,对分析窗内的信号进行傅里叶变换,从而得到信号的局部特征变化。若将分析窗函数γ(t)表示,则信号x(t)的STFT可表示为:

(4)
由式(4)可知,窗函数γ(t)的形状和宽度STFT的时频分辨率有一定的影响,窗函数一旦选定,其时频分辨率就固定了,STFT的时间分辨率与频率分辨率是相对矛盾的,窗函数越小,时间分辨率越大而频率分辨率越小,反之亦反。若以Δt代表时间分辨率,Δf代表频率分辨率,则根据Heisenberg测不准原理,二者的乘积必须满足:
(5)
由式(5)可知,同时满足任意小的时间间隔和任意小带宽的窗函数是不存在的,因此窗函数必须与需要达到的分析性能相适应。为获得较好的分辨率,采用长度为Nc/4的高斯窗函数对传统直接序列扩频信号与四维直接序列扩频信号的STFT分布进行分析,仿真结果如图 4所示。
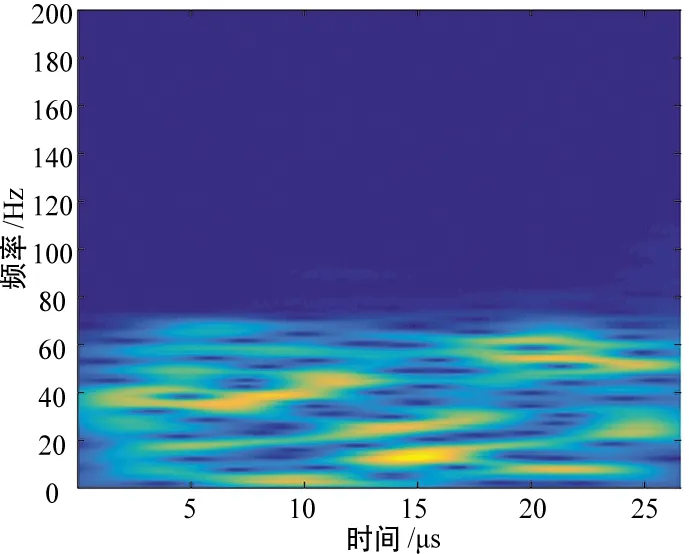
(a) 传统直扩信号STFT分布
由图4可知,由于两种调制方式均采用扩频的方式,信号时频聚集性较低,不能通过时频分布特性对两种调制方式进行识别。考虑到STFT的局限性,故也使用了Wigner-Ville分布与小波变换对两种调制信号的时频分布特性进行了分析,但是效果均不理想。
2 高阶累积量特征提取
调制信号的时频特征反映的是信号的二维特征,在信号的调制识别特征提取中,高阶累积量也可以反映信号之间的差异,而且高阶累积量对不同信号间的细微差异有较为良好的区分度,因此,基于高阶累积量的调制体制识别方法得到了广泛的应用[19]。不同阶的调制信号累积量其计算量也存在差异,因此,使用高阶累积量识别信号时,需要根据具体问题,采用合适的高阶累积量。
由于高斯随机变量对应的高阶累积量为零,因此,对于受高斯白噪声污染的数字信号,通过计算高阶累积量能有效降低信道噪声对信号特征参数的影响,提高信号识别准确度。
假定接收信号为n维随机变量(x1,x2,…,xn),则其联合概率密度函数为:
Φ(x1,x2,…,xn)=E{exp[j(ω1x1+ω2x2+…+ωnxn)]}。
(6)
对式(6)取对数,可得第二联合特征函数:
Ψ(ω1,ω2,…,ωn)=lnΦ(ω1,ω2,…,ωn)。
(7)

(8)
在信息序列x(n)独立同分布的情况下,可得k=p+q阶混合矩为:
Mp+q,q=E[xp(x*)q],
(9)
式中,x*为x的共轭。将高阶累积量定义为:
cp+q,q=cum[x,x,…,x,x*,x*,…,x*]。
(10)
由于高阶累积量与高阶矩之间满足关系:
(11)
所以,利用高阶矩来进行高阶累积量的计算,常用的高阶累积量为:
(12)
在实际分析中,得到通信信号的所有高阶累积量需要耗费很大的精力进行计算,只能通过对采样数据估计的方式减少计算过程,用累积量的估计值近似代替理论结果。因此,高阶累积量的近似表达式为:
(13)
由式(13)可知,信号的高阶累积量与其平均功率E有关,由于受到信号功率的影响,同类信号高阶累积量之间差异较小,导致无法有效识别。因此,为消除信号自身功率的影响,提高识别准确度,常利用不同累积量间的比值作为判别信号调制方式的参量,即
(14)
高阶累积量不仅描述了相关性,而且提供了一个差异度量,因此,可以利用两种调制信号的高阶累积量作为判别准则。两种调制信号的高阶累积量与信噪比的关系如图 5~图8所示。
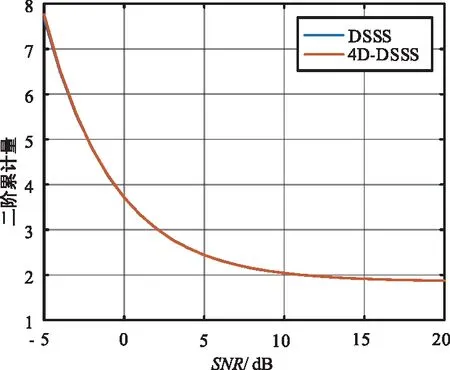
图5 调制信号二阶累积量Fig.5 Modulation signal second-order cumulant
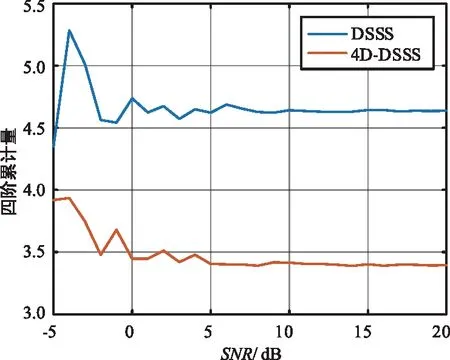
图6 调制信号四阶累积量Fig.6 Modulation signal fourth-order cumulant

图7 调制信号六阶累积量Fig.7 Modulation signal sixth-order cumulant

图8 调制信号累积量参数Fig.8 Modulation signal cumulant parameter
由图5~图8可知,当利用门限对两种调制信号进行识别时,两种调制信号的二阶累积量发生重叠,这是因为二阶累积量实质是调制信号的二阶距(均值),本质上DSSS信号与4D-DSSS信号服从相同的概率分布,因此其二阶累积量相等;调制信号累积量参数Fa在大信噪比条件下,信号的区分度较为明显,而在小信噪比条件下区分度不明显;只有两种调制信号的四阶累积量和六阶累积量区分度明显。因此,在利用固定门限对调制信号进行识别时,采用信号的四阶累积量和六阶累积量可以实现对调制体制的精确识别。
3 仿真分析
为了验证高阶累积量的有效性,采用蒙特卡洛的方式,对采用两种扩频调制体制的正确识别率进行仿真。仿真条件如下:
调制方式传统直接序列扩频,四维直接序列扩频;
基带成型升余弦函数(滚降系数:0.25,过采样率:20);
伪随机序列m序列;
传输信息量100 bit。
根据2节的理论分析,利用固定门限Th对两种调制体制信号进行识别,调制体制识别准则:① 利用四阶累积量识别,门限4.25,当累积量小于4.25时,接收信号为4D-DSSS信号,反之,接收信号为DSSS信号;② 利用六阶累积量识别,门限值45,当累积量小于45时,接收信号为4D-DSSS信号,反之,接收信号为DSSS信号。根据调制信号识别准则,对其识别性能进行仿真,仿真结果如图9所示。

图9 调制信号的正确识别率Fig.9 Correct recognition rate of modulated signal
由图9可知,调制信号高阶累积量的正确识别率随着信噪比的增加而增加,当信噪比SNR>-4 dB时,累积量正确识别率均达到100%;当SNR<-4 dB时,调制信号高阶累积量的正确识别率均较差,这主要是因为在小信噪比的情况下,调制信号中噪声所占比例较大,导致计算出的高阶累积量小于门限值,所以在小信噪比的情况下,高阶累积量的识别精度有所降低。从识别曲线的变化趋势上可知,四阶累积量的识别率高于六阶累积量。
考虑到随着阶数的增加,累积量的计算复杂度也有所上升。在实际中,算法计算量不容忽视,过高的计算量会对系统的实时性产生影响。不同累积量的计算复杂度如表 1所示。
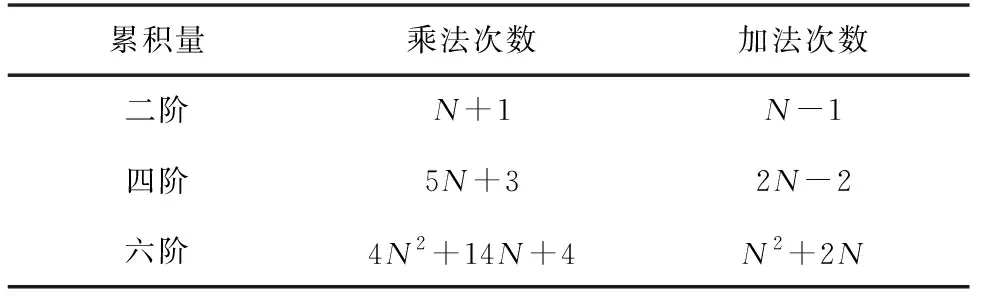
表1 不同累积量的计算量Tab.1 Calculation amount of different cumulants
由表1可知,二阶累积量和四阶累积量的计算量为O(N),六阶累积量的计算量为O(N2),由于六阶累积量中存在二阶矩与四阶矩的交叉项,计算量的增加,意味着算法处理信号的实时性降低,从而影响通信效果。因此,利用四阶累积量作为识别新旧扩频调制体制的依据,不仅实现了调试方式对调制体制可识别性的要求,也提高了系统的工作效率。
4 结束语
针对四维直接序列扩频调制技术可识别性问题,从基础信号层出发,分析四维直接序列扩频技术体制与传统扩频技术体制之间的区别,寻找可以区分两种调制体制的特征参量,达到自动区分识别调制信号的目的,实现新旧扩频技术互联互通。理论和仿真结果表明,DSSS信号和4D-DSSS信号的时频域特征对信噪比的变化较敏感,且两种信号同属宽带信号,其信号能量被极大地分散,所以利用时频特性无法分辨。DSSS信号和4D-DSSS信号的高阶累积量具有明显的区分度,特别是四阶累积量,当采用固定门限对两种调制信号进行区分时,具有极高的正确识别率,且较低的计算量有利于降低对硬件资源的消耗。

