基于神经网络的网络流量预测算法研究

虞丰檑，徐展琦，张林杰，杜 爽

(1.西安电子科技大学 综合业务网理论及关键技术国家重点实验室，陕西 西安 710071；2.中国电子科技集团公司第五十四研究所，河北 石家庄 050081)

0 引言

随着因特网技术的迅猛发展和网络业务的激增，需要有效的网络管理以提高网络服务质量[1]。网络流量作为网络管理与运营中的重要参数，对其进行准确预测有助于优化网络资源分配，减少网络拥塞并提高用户服务体验质量[2]。

网络流量预测模型分为线性与非线性两种，传统的线性模型包括自回归(AR)模型、移动平均(MA)模型以及自回归积分移动平均(ARIMA)模型[3]等，此类模型原理简单、易于实现。但是，随着网络业务的急剧增加和基础网络在规模、体制以及组网形态等方面的多样性发展，网络流量的自相似性、长相关性、重尾性和混沌性愈加明显，线性模型的预测误差较大。在预测具有复杂特性的网络流量时，非线性预测模型拟合能力强，性能明显优于线性预测模型，因此得到广泛应用。非线性模型主要包括基于小波的预测模型[4]、支持向量机(SVM)[5]以及神经网络(NN)等，其中的NN由于具有强鲁棒性和自学习特性，在流量预测中有较好的应用。例如，杜振宁[6]结合反向传播神经网络(BPNN)和布谷鸟算法进行网络流量预测，Song[7]等提出基于粒子群优化(PSO)算法的径向基神经网络(RBFNN)预测模型，Yang[8]等采用增强学习优化的长短期记忆神经网络(LSTMNN)进行超长期网络流量预测。

本文简述BPNN、RBFNN和LSTMNN的原理，利用这些NN预测不同时间尺度的网络流量，分析其预测方面的性能、优缺点和适用场景，试图为基于NN的故障预测和故障定位的学术研究及实际应用提供技术支撑。

1 神经网络模型原理

1.1 BPNN

BPNN示意图如图1所示，其输入层与输出层均是单层，隐含层可以是一层或多层，每层可包含若干神经元节点[9]，隐含层和输出层任意节点的输入值y均满足y=Wx+b，其中x为上一层输出，W为权值，b为偏置。BPNN是一种利用反向传播算法训练的神经网络，该算法将输出误差沿原来的连接通路返回到输入层，逐层调整网络节点的权值和偏置，使误差信号趋于最小[10]。

图1 反向传播神经网络模型Fig.1 Back propagation neural network model

BPNN可实现从输入到输出的非线性映射，且具有一定的自学习能力，已被广泛应用于预测领域；然而，反向传播算法本质上为梯度下降算法，可能导致学习速度慢，容易陷入局部最优，尚不适合预测相关性复杂的数据。

1.2 RBFNN

RBFNN结构如图2所示，其输入层、隐含层和输出层均为单层，隐含层节点和输出层节点的激励函数分别为径向基函数和线性函数[11]。

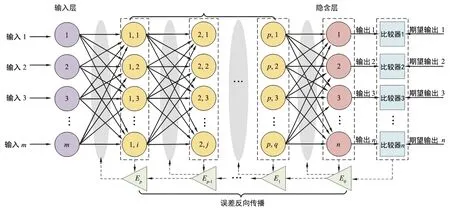
图2 径向基神经网络模型Fig.2 Radial basis function neural network model

RBFNN训练算法分两步：① 确定径向基函数(RBF)的中心点和宽度，常用方法包括K聚类[12]、模糊聚类以及自组织映射[13]等；② 通过梯度下降法或最小二乘法计算隐含层至输出层的权值。

RBFNN具有良好的非线性逼近能力和泛化能力，且隐含层至输出层的权值可通过最小二乘法得到，训练速度快；但是，其参数的选择会影响RBFNN性能，且根据不同问题确定相应的参数十分困难[9]。

1.3 LSTMNN

图3为LSTMNN结构示意图[9]，它是循环神经网络(RNN)的变体。RNN引入反馈机制[14]，提高对复杂时间序列的预测精度；针对标准RNN可能存在梯度爆炸或梯度消失，难以捕获时间序列的长相关性特征等问题，LSTMNN在RNN基础上引入门控机制，使其具备学习时间序列长相关性的能力。

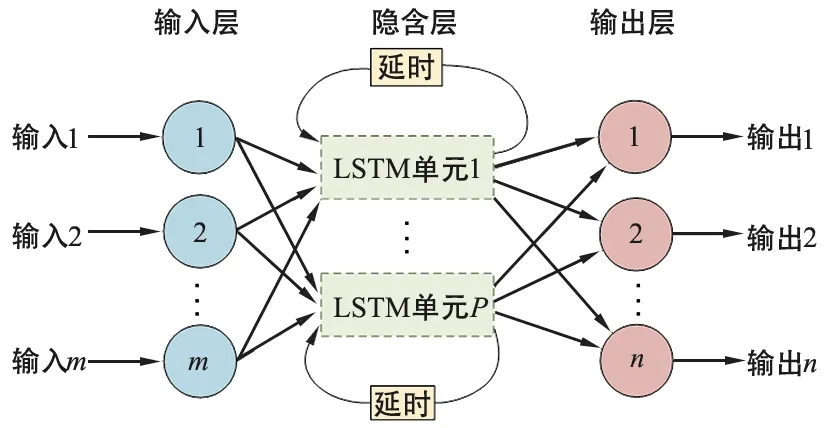
图3 长短期记忆神经网络模型Fig.3 Long short-term memory neural network model

如图4所示，LSTM记忆单元使用遗忘门、输入门和输出门以保持和控制单元的状态，“门”是一个选择性通过信息的结构。遗忘门将上一时刻隐含层状态ht-1和当前输入xt拼接得到的矩阵[ht-1,xt]输入到Sigmoid函数中(图中用σ表示)，决定保留或丢弃哪些信息；输入门将[ht-1,xt]同时输入到Sigmoid函数和tanh函数，两个结果相乘后得到的值决定输入到LSTM记忆单元的刺激强度，形成当前时刻记忆单元状态Ct；输出门将[ht-1,xt]和Ct分别输入到Sigmoid函数和tanh函数中，两个结果的乘积控制从这个记忆单元输出到外界的信息ht，最后把LSTM单元新状态Ct和新隐含层状态ht输出给下一时刻的LSTM记忆单元[9]。

虽然LSTMNN的记忆机制有利于对长期流量的精确预测，但计算耗时，该问题可由门控循环单元神经网络(GRUNN)改善。GRUNN作为LSTMNN的变体，将LSTMNN的遗忘门和输入门组合成更新门，同时合并记忆单元状态Ct和隐含层状态ht，使得GRUNN在保证预测精度的同时，减少训练参数，加快训练速度，已被广泛应用于具有长期依赖性的时间序列预测。

图4 长短期记忆单元Fig.4 LSTM unit

2 基于神经网络的网络流量预测

2.1 实验仿真环境及数据来源

本实验使用的系统为Windows 8.1，CPU为Core i5-5200U，GPU为AMD R5 M230，计算机编程语言为C++，集成开发环境是Microsoft Visual Studio 2019。

实验所用数据集来自英国学术骨干网(the UK Academic Network Backbone)，时间从2004年11月19日09:30:00至2005年1月25日00:30:00，第一个数据集按小时进行采集，第二个数据集按天进行采集，训练集与测试集的比例都为4:1。

2.2 网络流量预测实现

在利用NN对网络流量进行预测前，需要确定NN的结构参数。取输入层节点数为24，输出层节点数为1，隐含层数目和每层的节点数则是通过实验选取最优值，二者的取值范围分别为{1,2,4,8}和[5,21]。在进行实验前，先采用Min-Max归一化方法对流量数据进行处理，把数据映射到0～1范围内。

图5给出了3种NN的预测性能随隐含层节点数变化的趋势。由图5(a)可知，当隐含层节点数逐渐增加时，3种NN的MAPE先降低再升高，存在一个极小值点。当隐含层节点数过少时，NN拟合数据能力不足，导致预测精度较低；反之，当隐含层节点数过大时，NN容易陷入过拟合，导致预测精度下降，BPNN、RBFNN和LSTMNN分别在隐含层节点数为19、16和10时预测精度最高。由图5(b)可知，3种NN的运行时间随着隐含层节点数增加而成倍增长，这是因为隐含层节点数越多，NN的计算复杂度越高，程序运行时间越长。因此，综合考虑预测精度和运行时间，选择BPNN、RBFNN和LSTMNN的隐含层节点数分别为19、16和10。

(a) 隐含层节点对MAPE影响

RBFNN的隐含层数目为1，因此只比较隐含层数目对BPNN和LSTMNN预测精度及运行时间的影响。如图6所示，随着隐含层数目的增加，BPNN和LSTMNN的预测精度降低，运行时间增长。这源于过多的隐含层数目可能会使NN陷入过拟合，导致预测精度降低，同时增加NN计算复杂度和计算用时。因此，综合考虑预测精度和运行时间，BPNN和LSTMNN的隐含层数目为1时预测性能较好。

下面将分别用BPNN、RBFNN和LSTMNN这3种模型预测时间尺度为小时和天的网络流量。NN的预测精度采用均方根误差(RMSE)[15]、平均绝对误差(MAE)[15]和平均绝对百分比误差(MAPE)[16]。

(a) 隐含层数目对MAPE的影响

3 网络流量预测结果及分析

图7给出了时间尺度为小时的网络流量预测结果，由图可看出流量呈现周期性，周期为24 h，符合因特网用户的网络使用习惯，3条预测曲线都较好地拟合实际流量值。

表1给出了3种NN的预测精度及其相应的训练时间。在预测精度方面，由于LSTMNN的门控机制有助于捕获时间序列的特征，LSTMNN精度最高，RBFNN次之，BPNN最差；RBFNN相比BPNN可以任意精度逼近连续的非线性函数，具有良好的泛化能力，但由于缺乏记忆机制，预测精度较LSTMNN差；BPNN单纯使用梯度下降法，对非线性时间序列的拟合能力有限，因此相较于前二者，其预测精度最低。在训练时间方面，BPNN比RBFNN的隐含层节点数更多、计算复杂，RBFNN耗时最短，BPNN次之，LSTMNN所花时间最长；LSTMNN引入反馈系统和门控机制结构复杂，导致预测所花时间较长。

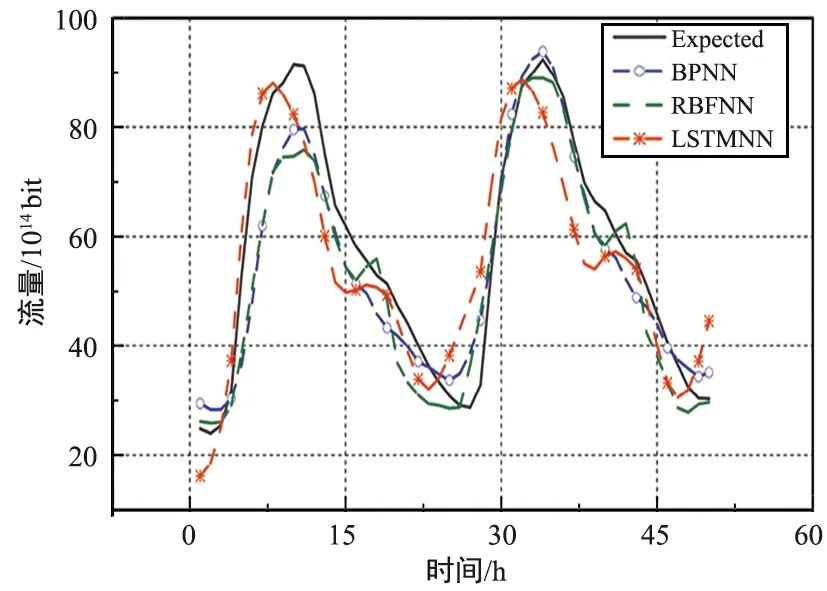
图7 不同神经网络的流量预测性能比较Fig.7 Traffic prediction performance comparison of different neural networks

表1 神经网络预测精度与训练时间Tab.1 Prediction accuracy and time consumed of neural networks

图8给出了时间尺度为天的网络流量预测结果，其同样具有周期性且周期为7天，LSTMNN预测结果较好地拟合实际流量值，而BPNN和RBFNN预测值与流量实际值走势相近，3种模型中BPNN相差最大。

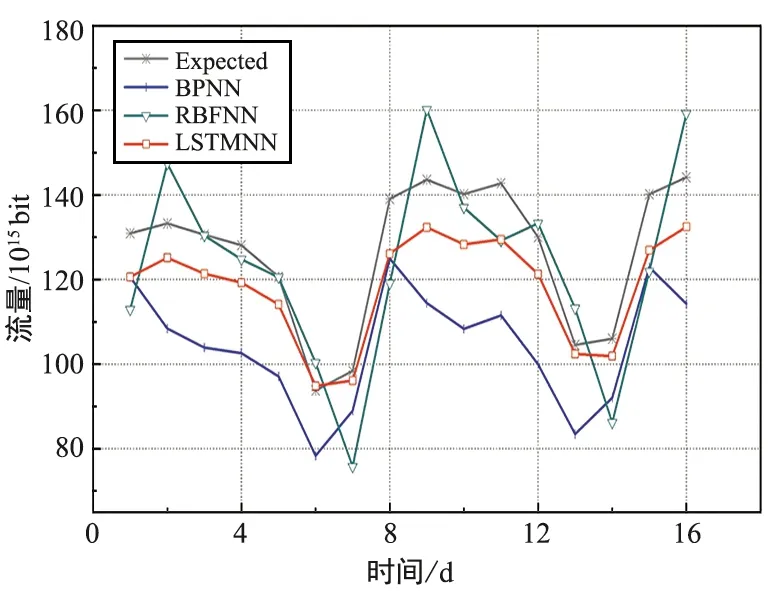
图8 不同神经网络预测性能比较Fig.8 Prediction performance comparison of different neural networks

表2列出了3种NN的预测精度和训练时间。当时间尺度为天时，网络流量数据的关联性降低，BPNN和RBFNN无法很好捕获数据的长期依存关系，导致预测精度降低；LSTMNN具有记忆单元，可以学习流量的长期特征，因此适合预测具有长相关性的流量。在训练时间方面，LSTMNN所花时间最长，但与BPNN和RBFNN的训练时间相差较小，这是由于时间尺度为天的网络流量数据数目有限，3种神经网络所耗费的时间差距不大。

表2 神经网络预测精度与运行时间Tab.2 Prediction accuracy and time consumed of neural networks

根据上述实验可知，BPNN和RBFNN具有良好的非线性拟合能力和自学习能力，但由于缺乏记忆机制，只适合短期网络流量预测；LSTMNN引入门控机制，能够学习时间序列的长期依赖性，更适合具有复杂特性的网络流量预测[17]。

4 结束语

本文将BPNN、RBFNN和LSTMNN应用于网络流量预测，研究超参数设置对3种NN预测性能的影响，并对比3种NN在各自最优超参数下的预测性能。在预测时间尺度为小时的网络流量数据时，3种NN预测精度大致相同，但对时间尺度为天的网络流量数据预测时，LSTMNN长期记忆的优势得以体现，其预测精度比BPNN和RNFNN高。通过分析以上3种神经网络的优缺点，并结合现有研究，可得到以下研究设想：

任何单一模型都有其适应场景，无法很好地刻画网络流量的真实特性，难免会产生比较大的误差；组合预测模型能够更加精确地反映真实的网络流量，通常具有更高的预测精度。例如，文献[18]以灰色理论、ARIMA和NN模型为基础，提出了一种固定权系数的组合预测模型，在相对误差与均方误差等方面均优于单一模型，有效性和可行性均高，值得进一步研究。

随着网络日益复杂化以及各类业务对传输质量(QoT)要求的提高，实现快速的故障预测和故障定位具有重要的实用价值，可利用NN强大的自学习能力分析网络特征参数，实现网络故障的精准预测与快速定位，大幅提高网络的智能运维性能。