基于双射软集合理论的压裂井层评价研究——以大庆油田A区块为例

魏 巍

（中国石油大庆油田有限责任公司井下作业分公司，黑龙江 大庆 163453）

A区块位于大庆油田杏树岗构造北部，含油面积约14.32 km2，地质储量约1 230.56×104t，油藏埋深1 080～1 620 m，目的层以三角洲前缘亚相沉积为主，储层厚度较薄，为低渗透油层。2016—2018年共计压裂42口井，压裂后与预期增产效果差异大，原因是前期的选井/层方法不当。前期主要选取井况正常、储层产液量低、含水低、注采完善、施工数据全面、处于钻关区等的探井作为备选压裂井，选井/层方法过于主观且缺少充分的数据支撑。当前，压裂井/层选择主要采用层次分析法[1]、模糊数学[2]、灰色关联度[3]、神经网络[4]等单一或结合的研究方法[5，6]，这些方法普遍存在参数不充分、模型复杂、数据处理复杂等缺陷。压裂施工效果受多种因素影响，不确定性较强，难于量化。本文引入的双射软集合理论在处理这类问题时有其独特的优势，通过给定评价对象一个近似描述，无需给出精确结果，同时模型简单，依靠其自身的数理关系确定权重，无需借助其他方法来确定权重，通过构建压裂井/层指标评价体系，得到优选结果，为后续的压裂井/层评价工作提供方法支持。

1 双射软集合理论

软集合理论[7]是由Molodtsov于1999年提出的一种分析和处理不精确、不完备信息的数学工具，双射软集合理论[7]是在此基础上提出的一种新理论。

定义1[7]：U为初始全集，E为参数集，当且仅当F是E所有子集的一个映射时，则称(F，E)为U集合的一个软集合。

定义2[8]：令(F，E)为U集合上的软集合。这里F表示B到幂集P(U)的一个映射关系，B为非空参数集合，那么(F,B)为双射软集合，其应满足：

对于任意参数ei，ej∈B且ei≠ej，并满足F(ei) ∩F(ej)=φ。

1.1 双射软集合决策系统

定义3[8]：假设(Fi，Ei)(i=1 ，2，3，···，n)是U集合上的n个双射软集合，其中，对于任意ei∩ej=φ(i，j= 1， 2，3，···，n；i≠j)，(G，B)是U集合上的双射软集合且B∩Ei=φ(i= 1 ， 2，3，···，n)称为决策软集合。设(F，E) =U(Fi，Ei)， 那 么 三 元 组((F，E)，(G，B)，U)被称作U集合上的双射软集合决策系统。

1.2 分明矩阵

定义4[8]：设S=(U， Λ(Fi，Ei))∪(D，C)是一个双射软集合决策表，那么M= (mij)n×n是此双射软决策的分明矩阵。(mij)n×n是一个n×n的矩阵，元素(mij)= {a∈C Ia(xi) ≠Ia(xj)} ，mii=0。

其中，C代表双射软集合决策系统中的决策集，a为C中的一个决策对象，aI代表其中的一个决策元素集，ix和xj分别代表不同的评价对象。

1.3 双射软集合参数约减

定义5[8]：给定一个决策信息系统的分明矩阵W= Ui，j=1，2，3，···，n(mij)，满足如下条件：

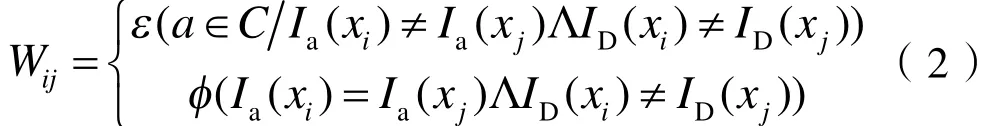
式中：ID为目标决策元素集；Ia为其中的一个决策元素集；φ为空集；ε为分明矩阵中的元素。

式 （2） 中 ，(xi，xj)∈n×n，mij≠φ⇒W∩mi j≠φ。若A是决策信息系统中的一个参数集合，且A∈W，那么W-{A}可以从W中删除，通过这一过程得到双射软决策参数约减。

1.4 双射软集合参数依赖度及重要程度关系

定义6[8]：假设三元组((F，E)，(G，B)，U)是一个双射软决策系统，其中，(F，E) =U(Fi，Ei)为双射软集合系统，(F，E)被称作条件双射软集合，那么 (F，E) =U(Fi，Ei)与(G，B)的依赖度称为双射软集合决策系统的依赖度，可表示如下：e(Λ(Fi，Ei)，(G，B))。

存在一个双射软集合(F，E)[7]，有如下表达式：

式中：i为决策分割数；j为决策分割区间数；k为目标决策分割数，wij= maxr，tk= maxt；ck为决策分割对象集；cij为决策评价对象集；ej为评价对象的依赖度。

式（3）和式（4）分别表示决策分割与目标决策分割之间的重要程度关系，式（5）为权重计算公式。

1.5 算法流程

第一步，构建基于双射软集合的模型决策系统；

第二步，根据定义4及定义5得出模型的分明矩阵及相对参数约减（保留重要参数）；

第三步，根据定义6、式（3）及式（4）得出各参数之间的相对依赖度及重要程度关系；

第四步，根据式（5）得出最终的决策权重，算法结束。

2 实证研究

本文选取大庆油田A区块已实施压裂的10口井对双射软集合理论的可行性进行验证。按照采出程度、生产压差、地层压力等15个参数设定指标评价体系，根据该区块的各参数数据库绘制油井的信息，如表1所示（其中，数字1代表双射软集合的参数表述方式，无数理意义）。

表1 指标评价信息

根据定义4和定义5得到大庆油田A区块的分 明矩阵如下：

由式（2）得出重要参数为地层压力、渗透率、含油饱和度、可采储量、加砂强度及施工排量。根据定义6得到各参数对应的依赖度分别是0.2、0.3、0.3、0.4、0.6和0.5。

通过式（3）和式（4）得出决策分割与目标决策分割之间的重要程度关系，以评价对象x1井为例：

根据式（5），可得出该评价对象的权重排序w1= 1 .085 0，同理可得其余9口井的最终权重排序如表2所示：

表2显示的数据计算结果，为当前的压裂井改造顺序提供了可靠的数据支持。其中，x1，x2，x8井权重值都超过1，应确定为优先进行压裂措施改造的井；x4，x7，x10井权重值都超过0.9，应确定为备选压裂井；x3，x6井权重值稍低，可确定为谨慎压裂井；x5，x9井权重值最低，不宜压裂。

表2 参数重要程度关系及排序

同时，调取该10口井压裂施工后初期日增加油量数据，如表3所示：

表3 压裂后初期日增油量

从表3中可以看出，各油井之间在增产方面虽存在部分差异，但都有一定的效果。其中x1，x2，x8井压后的日增油量最明显，x4，x7，x10井压后增产效果稍逊，x3，x6井压后也有一定的增产效果，x5，x9井增产效果最差。

3 结论

运用双射软集合理论对大庆油田A区块进行压裂选井评价，通过优选评价参数、依赖度、重要程度等得出权重排序，结论显示x1，x2，x8为优先压裂井，x4，x7，x10为备选压裂井，x3，x6为谨慎压裂井，x5，x9为不宜压裂井，将该评价结果与压裂后增油量数据进行比较，进一步证实了本文方法的科学性和可靠性。