深度教学，需要打开“视界”

周卫东

摘要：深度教学的发生要满足一些基本要义：深刻理解知识内涵，主动建构意义系统，解决真实情境中的问题以及建立学科思想等。要想使深度教学真正发生，教师需要沉入学科，打开“视界”，可以引导学生在内容的“边界”处探一探，在开阔的“空间”里创一创，在熟悉的“风景”中挖一挖，还要在生成的“浪花”中引一引。

关键词：深度教学;小学数学;深挖内容;开放探究;捕捉生成

“深度教学”是时下教育界的一个热词。许多教育理论工作者和一线教师都对此做了一定程度的追问，形成了许多研究成果，这对教育教学改革起到了积极的推动作用。什么是深度教学呢？在林林总总的解读中，我特别认同华中师范大学郭元祥教授的提法：“深度教学不是指无限增加知识难度和知识量，而是克服对知识的表层学习、表面学习和表演学习以及对知识的简单占有和机械训练的局限性，基于知识的内在结构，通过对知识完整、深刻的处理，引导学生从符号学习走向学科思想和意义系统的理解与掌握，并导向学科素养的教学。”由此可以看出，深度教学的发生要满足一些基本要义：深刻理解知识内涵，主动建构意义系统，解决真实情境中的问题以及建立学科思想等。要想使深度教学真正发生，我们需要沉入学科，打开“视界”，多“探一探”“创一创”“挖一挖”“引一引”。

一、在内容的“边界”处探一探

知识是具有生长性的。生长中的知识不仅有着“现在时”，也有着“过去时”与“将来时”。在常态的“网格化”教学中，许多教师在内容的边界问题上比较犹豫，轻易不敢越过教学目标所框定的“红线”，因而，错失了引发深度教学的时机，也失去了促进学生经验生长和思维进阶的机会。

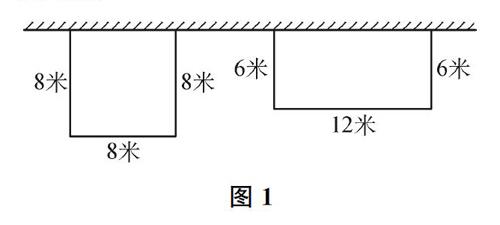
苏教版小学数学五年级上册《解决问题的策略》单元的第一个例题是：“王大叔用22米长的木条围一个长方形花圃，怎样围面积最大？”教学时，教师会引导学生用一一列举的策略得出“当长和宽最接近时，面积最大”的结论。例题教学后，作为巩固与拓展，教师一般会给出一道习题：“王大叔用24米长的木条一面靠墙（墙足够长）围一个长方形花圃，怎样围面积最大？”实际教学中，不少教师往往蜻蜓点水地满足于学生用一一列举的策略得到正确的结果，甚至直接布置学生课后思考。每及于此，我都有一种意犹未尽的感觉。

可不可以带领学生往前再跨一步，让他们不止于得到结果，而真正弄清其中的道理呢？祝元圆老师的尝试让我大开眼界。

出示上述习题后，让学生用自己的方法尝试解决。一部分学生由例题解决中获得的结论“当周长一定时，长和宽最接近，面积最大”直接推理，得出“围成一个正方形面积最大，这时正方形的边长是8米，面积是64平方米”的答案。另一部分学生用一一列举的策略得出“當宽是长的一半时，面积最大，此时长是12米、宽是6米，面积是72平方米”的答案。

“现在有两种答案，显然，面积是72平方米是对的，那么，面积是64平方米到底错在哪里呢？”围绕这个问题，引导学生画出直观图（如图1），再对比分析：木条只占三条边，如果围成正方形，则算上墙后周长是32米;如果围成长方形，则算上墙后周长是36米。这显然脱离了“周长一定”的前提条件，故此时正方形的面积与长方形的面积没有可比性。

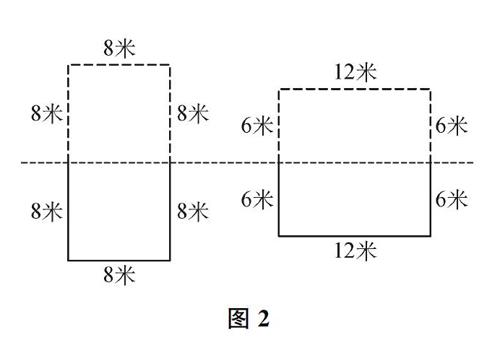
“那么，怎么满足‘周长一定的前提条件呢？”围绕这个问题，引导学生通过想象把墙“打通”，画出另一半，组成新图形（如图2），再思考分析：此时两个图形的周长是一定的，都是48米;前者变成一个长方形，面积是16×8=128（平方米）;后者变成一个正方形，面积是12×12=144（平方米）。这样，就符合“当周长一定时，长和宽越接近，面积越大”的原理了。

这样的教学中，学生通过尝试、生疑、释疑等过程，从现象到机理、从表面到深层、从模糊到清晰、从混沌到有序，弄清了数学知识背后处于“潜在”状态的基本原理，使课本知识得到了升华、学习边界得到了拓展。

二、在开阔的“空间”里创一创

深度教学呼唤“打开的”教学。这里的“打开”不仅意味着学习内容的打开、学习目标的打开，也意味着学习空间的打开、学习方式的打开。

《正、反比例》单元复习课上，严兵老师呈现了“乌鸦喝水”的画面（如图3），提出了一个大问题：“大家已经学过了正、反比例的图像。请大家想象一下，如果图像的横轴表示乌鸦喝水的时间，纵轴表示瓶内水的高度，你能根据图画中的情景，结合自己的想象，绘制出一幅图像吗？”随后，给出大量的时间，任由学生想象、创作。

接下来的交流可谓精彩纷呈、创意无限。小林画出了下页图4，解释说：“开始时，水位在水瓶高度的二分之一左右;乌鸦想了一会儿才想出办法，说明有一段时间水位没有变化;然后，乌鸦衔来了一个个小石子放入瓶中，水位上升;后面放石子越来越熟练，加上瓶口较小，水位上升速度较快;水位快到瓶口时，乌鸦开始喝水，一直到喝不到为止;乌鸦喝水后的水位应该不低于一开始的水位。”而小勇则画出了下页图5，他的解释是：“乌鸦在刚能喝到水的时候，便迫不及待地喝了;喝到不能喝的时候，便再去衔小石子。”

在欣赏了几幅创想作品后，严老师又呈现了一幅学生作品（如图6），启发思考：“有一位同学是这样画的，大家分析分析，有没有道理？”有了前面大量的创作、分享经验做支撑，学生很快找到了图6的问题所在：“乌鸦喝水后的水位一定不会低于喝水前的水位，而图像上喝水后的水位低于喝水前的水位，所以错了。”

数据科学家Mike Loukides认为：“数据科学家收集数据，把数据融入易懂的形式中，让数据讲故事，并且把故事讲给别人听。”虽然各版本小学数学教材都没有提出函数图像的具体教学要求，但是函数图像对六年级的学生来说没有太大的难度，并且形象逼真的样子、动态呈现的关系对他们具有较大的刺激。严老师的教学正是抓住了这样的素材与契机，融入故事，植入道理，让学生在新奇刺激、亲切有趣的学习环境中大胆创想、对比分析。由此，学生所获得的除了对“正、反比例”相关知识的巩固和深化外，更有想象力的提升、思维能力的进阶以及数学意识的增强。这样的教学，应该是深度教学应追求的美好模样。

三、在熟悉的“风景”中挖一挖

传统教学常常陷入“从来如此”“浅尝辄止”“点状思考”的窠臼，而深度教学解决的主要就是此类问题。所以，我们的教学要善于从“熟悉的地方”看到风景，从“一马平川”中看到奇崛，从“星星点点”中看到联系，从而走向深刻。

教学《千以内数的认识》一课，王茜老师花了较多的时间带领学生研究365的组成及读写，从而帮助学生建构数的意义，形成数感。当学生用板条图、计数器和研究单这三种方式展示了研究过程之后，王老师抛出了这样的问题：“刚刚我们用三种方法研究了365，好好比较一下，这三种方法有哪些不同的地方？有没有一些联系呢？”然后，聚焦其中的“3”，让学生在三种方式中找一找“3”在哪儿。在多层次的对话中，学生意识到：同样是300，在不同的地方，表示的方式不一样，可以是看得到、有形象的小方块，也可以是半形象、位值化的算珠，还可以直接写成更抽象的符号。最后，王老师巧妙点拨：“从小方块到算珠再到数，你们有没有一些感受呀？”在学生回答的基础上，相机渗透：“是啊，数学家们研究数学、小朋友们学习数学，都要经过一个慢慢简化、慢慢抽象的过程。”

反观很多类似的课例，教师往往会将小棒、板条图、算盘、计数器、研究单等能用的材料全用上，使现场表现很开放，也很热闹;但是，方法多样不一定有用，开放、热闹不一定有“神”。这里的“神”是蕴含于现象中的知识本质、經纬于知识间的学科思想。

教学《分数的意义》一课，王小波老师在学生填空（如图7）后，提出问题：“同样是4个圆片，为什么表示的数却不一样呢？”学生的回答渐次逼近本质：“标准不一样了。”“看作1份的数变了。”“度量的标准不同。”……教师追问：“此时，我们怎样看待这里的‘1？”学生彻底激活了思维，自觉厘清了作为自然数的1与作为“1份”的1是不一样的，所以要给后者加上引号。这样的教学中，概念的内核被剥开，被顺应、被同化，学习自然而然走向深处。

反观很多类似的课例，教师往往囿于课本照本宣科，在学生经历了用一个物体、一个计量单位、一些物体组成的整体表示四分之三后，直接讲授：“同学们，一个物体、一个计量单位和一些物体组成的整体，数学上可以用同一个名称来概括，那就是单位‘1，明白了吗？”在软弱无力的“明白了”之后，教学继续推进。这样的教学没有从知识的本源处追问：为什么叫单位“1”呢？1上面为什么要打引号呢？怎样理解单位“1”的含义呢？因而就不符合深度教学的基本要义。

四、在生成的“浪花”中引一引

深度教学不是僵化的教学，而是“活”的教学;不仅仅是基于预设的教学，更是面向学情、应对生成（带有评价反馈性质）的教学。因而，捕捉意料之外的生成性资源，也是深度教学的应有之义。

教学《加法的交换律》一课，一位学生提问：“老师，加法结合律（a+b）+c=a+（b+c）中，左边的括号可以不写吗？为什么课本上这么写？这当中藏着什么秘密吗？”小小的“石头”却砸出了不小的“浪花”。教师把这个生成的问题抛给学生，没想到引来了许多有价值的思考与回应：“突出了运算规则。”“这样更美了！”“像大人喝酒，小括号表示有人在敬酒，其他人别瞎掺和;没有括号表示都坐着，就不知道谁想敬谁了，有多种可能。”……可见，如果我们多一些审视的眼光和意识，可能真的会捕捉到意料之外的美好。更重要的是，教学中教师不仅要自己捕捉，更要让学生捕捉。

一次单元复习课上，我即兴编了一组口算题（如图8）让学生算，旨在提高学生的口算速度，增强学生的运算技能。计算出结果后，小焦举手：“老师，您黑板上的式子可以调整一下。”我一激灵，随即回应：“怎么调整呢？”她说：“把80÷5=16与90÷5=18对调一下。”我问：“为什么要对调呢？”学生一起喊起来：“对调一下更好！”“对调一下就可以研究其中的规律了！”于是，我顺水推舟：“那么规律到底是什么呢？大家先想一想，待会儿来讲一讲。”随着学生的讲解，黑板上留下了清晰的思维过程（如图9）。

然后，我适时推进——

师前面我们研究的内容叫“商不变的规律”，那这个叫什么？

生除数不变的规律。

师是啊，这么小小地调整一下，一个重要的规律就显山露水了。你觉得这样的式子怎么样？

生很整齐。

生很美！

师美在哪儿呢？

生方便我们观察后找规律。

生美在很工整。

师是啊，这样的美就是数学美中的规律美。每个人都有“向美”的本能，生活中不是没有美，而是——

生缺少发现美的眼睛。

黑格尔认为，“美是感性的理性显现”。数学美是一种独特的美，它广泛地“隐匿”在数学的内容和教学过程中。数学美常常发生在深度教学中，需要我们存乎一心，顺其自然，抓住那些可遇而不可求的教学瞬间，相机引发，留下弥足珍贵的美的感悟。

参考文献

[1] 郭元祥.论深度教学：源起、基础与理念[J].教育研究与实验，2017（3）.