基于非概率集合理论的屋面板风致疲劳寿命估计

孙大奇，朱 颖，刘晓光，双 妙

(1. 中国铁道科学研究院，北京 100081；2. 中国铁道科学研究院集团有限公司铁道建筑研究所，北京 100081；3. 高速铁路轨道技术国家重点实验室，北京 100081；4. 国核电力规划设计研究院有限公司，北京 100095)

1976 年Morgan 和Beck[1]对澳大利亚达尔文地区的风灾调查和实验研究中指出，金属屋面板的风致疲劳是Tracy 飓风造成损失的主要因素。然而，现有研究成果多集中于风荷载极值取值和结构在极值风荷载作用下的强度计算和变形校核，对疲劳损伤问题研究不足。由于屋盖结构的气动外形，来流在金属屋面板上形成特征湍流，使结构在屋盖边缘受到很大的交变应力，忽视疲劳设计会造成严重的损失。

现有的结构疲劳分析方法大致可以分为时域方法和频域方法，时域方法是从结构响应的应力时程出发，利用计数法直接提取结构响应的应力幅后，根据常幅S-N 曲线和变幅疲劳寿命预测的修正线性Miner 准则，对结构疲劳寿命进行估计[2]。而频域方法是通过随机振动理论由荷载的功率谱密度得到结构响应的应力功率谱密度，对于窄带过程按单位时间内超越零界限的期望率估计疲劳寿命，对于宽带过程则按极大值次数的期望值计算疲劳寿命[3]。

风致疲劳估计方法最初由Davenport[4]提出，建立在频域疲劳分析方法的基础上，假定结构在风载作用下的应力响应服从窄带高斯分布，根据窄带高斯过程的极值满足瑞利分布，依据Wirsching的经验公式[5]计算疲劳损伤，并假定平均风速满足Weibull 分布进而得到结构的风致疲劳寿命[6]。

由于频域疲劳分析方法的一些局限性，各国学者采用时域方法对金属屋面板的风致疲劳问题进行研究。Xu[7]结合实测数据与风洞试验数据，采用S-N 曲线与Miner 准则对屋面板气动外形和特征湍流对疲劳寿命的影响进行了系统性的研究。Kumar 等[8]根据目标地区长期风环境和屋盖疲劳实验数据的特点，采用数值模拟的方法得到结构的风压时程后，应用Miner 准则和Goodman方法对屋盖结构的风致疲劳进行预测。

上述金属屋面板风致疲劳研究中，各国学者多关注风荷载的随机特性，忽略了金属屋面板由于施工误差或材料离散性引起结构本身的不确定性。结构的疲劳失效是受大量不确定因素影响的复杂过程，主要包括结构参数、外荷载和模型的不确定性[9]。考虑疲劳分析的复杂性，即使相同的荷载作用于相同的结构，结构疲劳寿命一般也不相同，且疲劳破坏通常会发生于结构最薄弱处，而材料间的个体差异和施工质量均会影响疲劳寿命。综上所述，仅考虑荷载的随机性而忽略结构的不确定性对结构疲劳寿命估计是偏于不安全的。

为考虑结构不确定性对疲劳损伤的影响，朱颖等[10-12]将结构不确定参数定义为区间变量，在宽带频域疲劳损伤的基础上提出了疲劳损伤区间估计方法。在此基础上，本文结合金属屋面板表面风压特性和工程所处地区风环境特性，在考虑结构参数不确定性的条件下，将区间分析方法引入时域疲劳损伤估计中，通过时域区间动力响应分析和疲劳损伤累积理论，得到金属屋面板在脉动风荷载作用下的疲劳寿命区间。

1 问题描述

工程结构中通常采用概率模型定义结构自身由于安装误差、材料个体差异等因素引起的不确定性问题。在没有足够统计数据或合适概率模型的条件下，概率方法描述结构自身不确定性并不适合。同时，工程结构的不确定性通常是由于误差或主观认识不足造成，并不具有随机特性。

对于金属屋面板的疲劳损伤问题，由于受制造质量和安装精度等因素的影响，疲劳寿命估计中仅能给出相关参数的区间范围。这使得采用区间分析方法定义参数的不确定性，提供了一种解决金属屋面板风致疲劳寿命估计问题中，考虑结构不确定性的新思路。

根据结构动力学和区间分析方法，考虑金属屋面板结构整体矩阵M、C、K 随不确定参数αj变化，屋面板在风荷载作用下的动力响应方程可表示为：

式中：M(α)、C(α)、K(α)分别为结构的质量矩阵、阻尼矩阵和刚度矩阵，均为不确定参数向量α 的函数；F(t)为结构的等效结点荷载，可分解为均值荷载μF和脉动荷载f(t)；应力均值区间按区间静力方法计算[13]，并根据Goodman 公式修正；u(α,t)、u˙(α,t) 和u¨(α,t)分别为结构的节点位移、速度和加速度，均为不确定参数α 的函数。不失一般性，采用Rayleigh 阻尼模型定义金属屋面板的阻尼矩阵，即：

式中，a0和a1为Rayleigh 阻尼系数。

求解式(1)，并根据Mindlin 板壳理论，金属屋面板任一点处的应力区间可表示为：

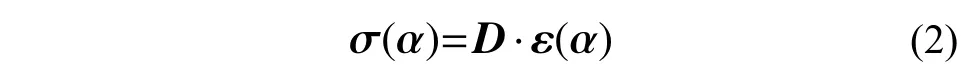
式中：σ(α) = [σf(α) σc(α)]T，σf(α)和σc(α)为弯曲应力和剪应力；ε(α) = [εf(α) εc(α)]T，εf(α)和εc(α)为弯曲应变和剪应变，分别表示为：

其中，弯曲应变和剪应变分别表示为：

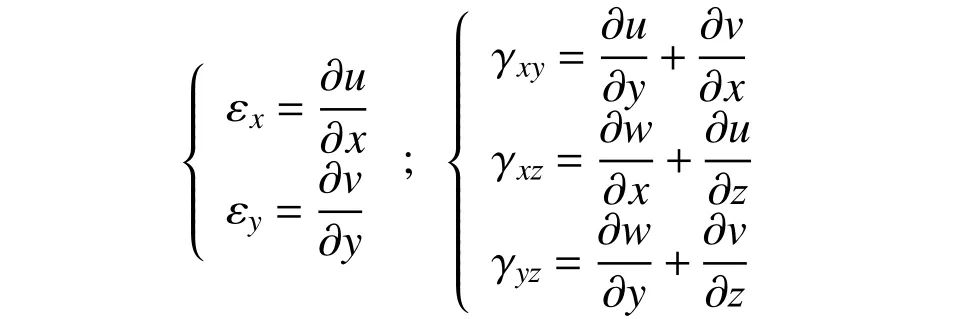
D = Trace[DfDc]，为弹性矩阵。其中：Trace[·]为矩阵的迹；Df和Dc为弯曲弹性矩阵和剪切弹性矩阵，分别表示为：

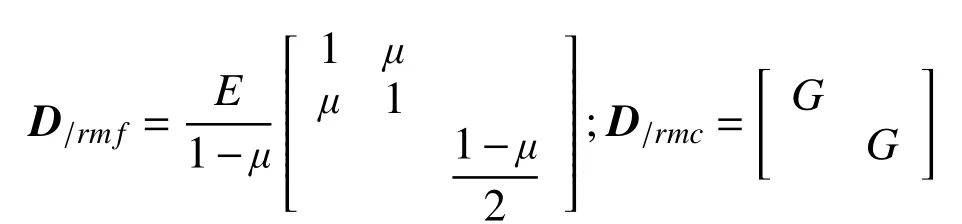
式中，μ和G 为泊松比和剪切模量。

金属屋面板在脉动风荷载作用下的疲劳损伤是典型的多轴应力状态下的疲劳问题。针对多轴应力状态下的疲劳问题，需要确定等效多轴应力或者破坏临界面上的正应力/切应力。本文采用Mises应力作为多轴应力下结构疲劳破坏的等效应力[14]，在平面应力状态下，Mises 应力表示为：

式中：σ(α)=[σx(α) σy(α) τxy(α)]T；Q 为常数矩阵，表示为：

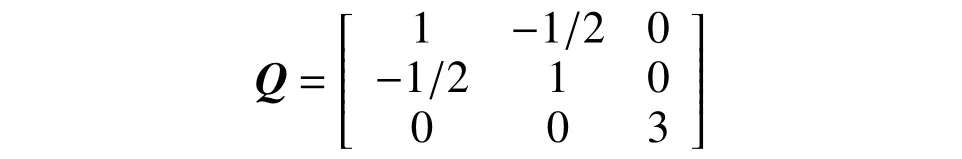
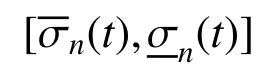
根据雨流计数法，金属屋面板的疲劳损伤表示为：

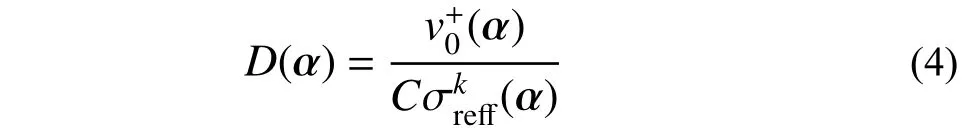
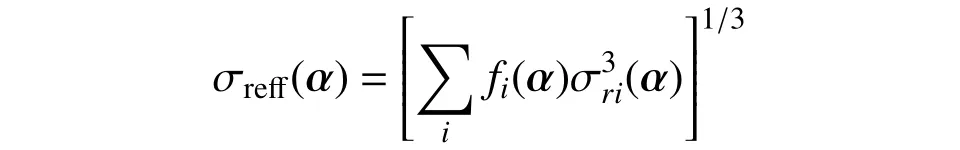
式中，fi(α)和σri(α)分别为等效应力的循环频率和幅值。

与极值问题和频域疲劳问题相同，考虑金属屋面板参数不确定的时域疲劳寿命估计将转化为计算不确定结构疲劳损伤或疲劳寿命的区间界限。根据线性损伤累积理论，金属屋面板在风荷载作用下的疲劳寿命区间，表示为[10,15]：

2 不确定结构区间动力响应

2.1 改进区间分析

Alefeld G 和Herzberger J[16]将基本运算、函数与实数区间相结合，提出区间分析理论用于解决实数有界区域的计算问题。为克服区间乘法运算过大的估计区间宽度、减小“依靠现象”的影响，在区间分析理论中引入单位对称区间(Extra Unitary Interval, EUI)，则区间变量的名义值α0,i和半径Δαi分别表示为[17]：

2.2 不确定结构的区间矩阵

根据摄动理论，当定义结构不确定参数αi是区间变量时，结构单元刚度矩阵可近似取一阶Taylor 级数，表示为：

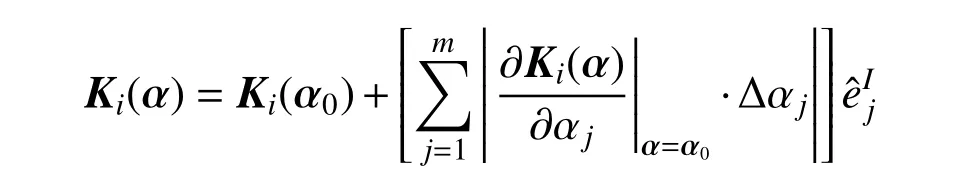
类似于有限单元法集成结构的整体矩阵，不确定的结构整体区间矩阵可表示为：

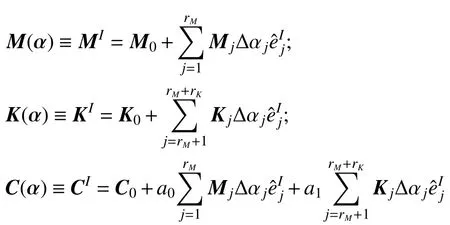
式中：rM和rK分别为质量和刚度矩阵的不确定变量数；M0、K0和C0分别为质量矩阵、刚度矩阵和阻尼矩阵的名义值；Mj和Kj为质量和刚度矩阵关于不确定参数αj的灵敏度矩阵，分别表示为：

如果不确定参数ρj是结构矩阵的非线性函数，则需要将ρj等效为结构矩阵的线性函数αj。例如，桁架结构的杆件长度lj是不确定参数，对于结构的抗侧刚度可将其等效为线性参数αj= 1/lj。

2.3 不确定结构区间动力学方程

根据非概率集合理论区间分析方法，不确定参数α 可以用区间向量表示。区间分析的动力响应问题，实质就是计算不确定结构在确定性荷载或随机荷载作用下，结构响应的上界与下界。采用区间泰勒公式[18]，假设不确定参数为微小变化的参数，取一阶泰勒公式，可得uI(α, t)的线性近似，表示为：

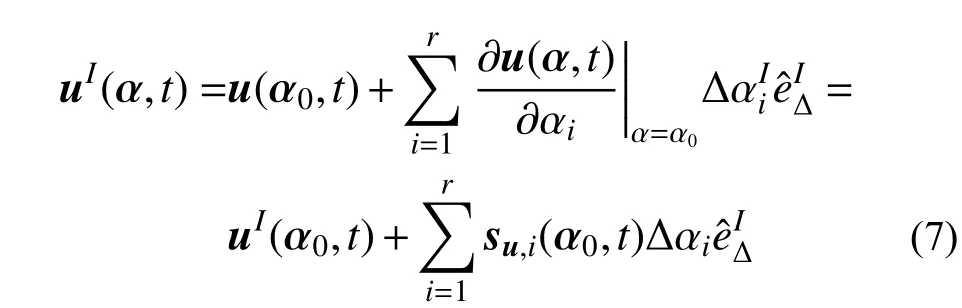
式中：u(α0, t)为结构的名义值响应向量；su,i(α0, t)为结构的一阶灵敏度向量。这样，结构动力响应的上界与下界就表示为：

由式(8)可知，只需要知道结构动力响应的名义值u(α0, t)和不确定性参数αi的灵敏度su,i(α0, t)就可计算结构动力响应的区间[19]。

2.4 不确定结构区间动力响应分析

不失一般性假设结构阻尼为经典阻尼，根据振型分解法：

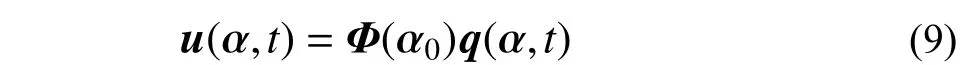
式中：Ф(α0)为n×m(m≤n)的矩阵，表示结构的前m 阶振型；q(α, t)为结构的前m 阶模态的振型坐标；Ф(α0)和q(α, t)可通过求解结构名义值的特征方程得到结构名义值的特征值和特征向量，将特征向量关于质量矩阵正则化，即：

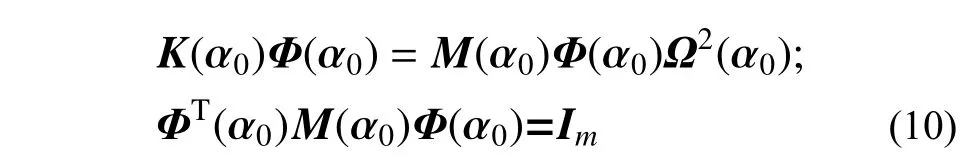
需要注意的是，式(9)是基于结构名义值的振型和频率的特征方程，即假设结构名义值的刚度矩阵关于有界但不确定参数α 的变化范围较小。

根据式(9)和式(10)，有界但不确定参数 αi的灵敏度可按振型分解方法表示为[20]：

将式(9)代入式(1)，得关于振型坐标的二阶常微分方程组，即：

其中：

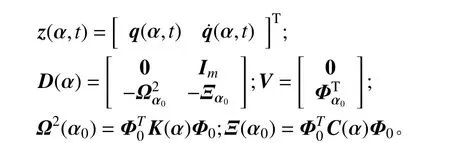
计算式(12)关于不确定参数αi的导数，并假定α = α0，则可得到关于有界但不确定参数αi灵敏度的二阶常微分方程组，即：

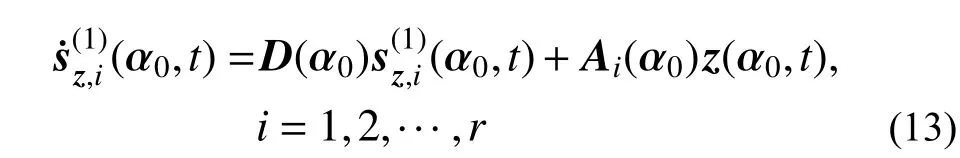
其中：

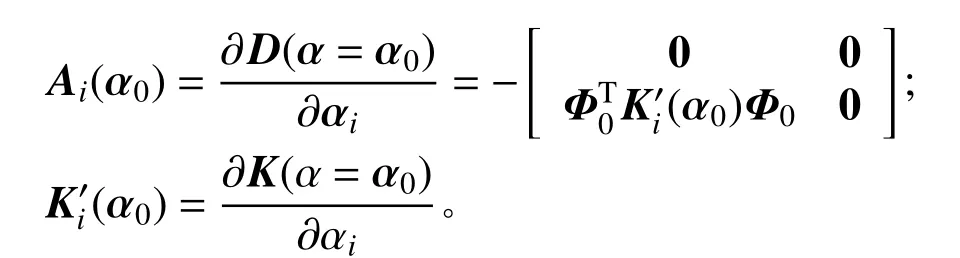
对于式(12)和式(13)可采用无条件稳定算法[21]计算结构的名义值和关于不确定参数的灵敏度值，即：

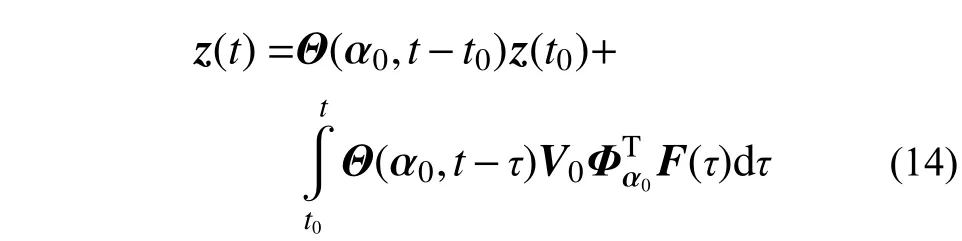
式中，V0为2m×m 矩阵，称为布尔(Boolean)矩阵，表示为：

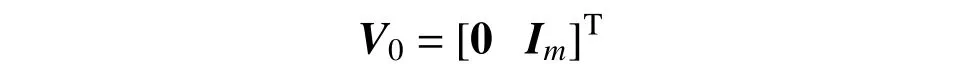
Θ(α0, t)称为转换矩阵，对于小阻尼结构可表示为[22]：

式中，h(t)和g(t)都是对角矩阵，其对角线元素表示为：

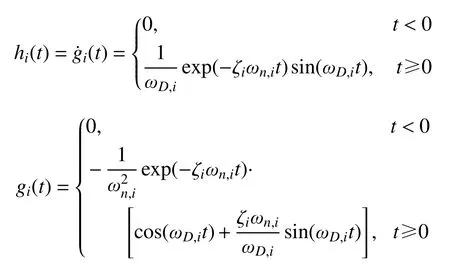
式中：ωn,i为无阻尼结构的第i 阶圆频率；ωD,i为有阻尼结构的第i 阶圆频率，ωD,i= (1-ζ2 i)1/2ωn,i。

通常情况下，式(14)中的卷积很难得到闭合解，需要通过数值方法计算。将外荷载在时间间隔(tk, tk+1]内分段线性插值，则每个时间间隔Δt内均满足：

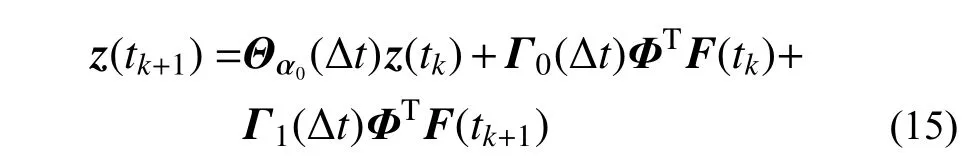
其中：

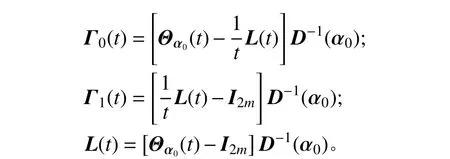
只需将式(14)的结构名义值响应z(α0, t)换成sz,i(α0, t)，类似的按照式(14)和式(15)即可得到不确定参数的灵敏度值。由z(α0, t)和sz,i(α0, t)按照式(8)和式(11)的振型叠加即可得到结构在动力荷载作用下响应的名义值和一阶灵敏度，再按照式(8)即可得到结构的位移响应区间。

3 金属屋面板疲劳寿命区间估计

将式(8)位移响应区间代入式(2)和式(3)中，得到考虑结构参数不确定条件时金属屋面板在风荷载作用下的应力响应区间。根据式(4)和式(6)，金属屋面板的风致疲劳损伤和寿命的上界和下界可表示为：

需要指出的是，如果待求解问题的不确定参数变量数为N 时，采用顶点法(vertex method)需要进行2N次动力响应分析和疲劳损伤估计。与频域疲劳区间分析中的完全混合方法类似[11-12]，本文提出的考虑结构参数不确定条件下金属屋面板风致疲劳损伤/寿命分析方法，仅需要一次动力响应分析即可计算金属屋面板的疲劳损伤/寿命的界限，提高了结构疲劳损伤估计的计算效率。

4 脉动风荷载

如图1 所示，金属屋盖结构的表面风荷载以风吸力为主，且靠近迎风面屋盖前缘的风吸力较大，并向下游方向逐渐减弱。根据流动机理，通常将屋面分成分离区、再附区和尾流区三部分。由于分离区和再附区的风荷载表现明显的非高斯特性，且风荷载数值远大于尾流区。因此，为本文选用UWO 风洞实验数据库中分离区和再附区实测风压系数谱作为风荷载目标谱。通过谐波叠加法和非高斯穿越过程[23]，模拟生成金属屋面板表面非高斯压力系数，则金属屋面板表面风压与风压系数、平均风速可表示为：

式中：Cp(t)为压力系数；Umean为平均风速；ρ 为空气密度。

图 1 大跨屋盖结构表面特征湍流Fig.1 Turbulent characteristics of large-span roof structures

图 2 模拟的非高斯风压系数时程图Fig.2 Simulated non-Gaussian time histories of wind pressure coefficients

图2 所示为由金属屋面板不同位置处压力系数功率谱密度按谐波叠加法和非高斯穿越过程模拟的非高斯压力系数和概率密度函数。为消去动力响应的初始状态，时程长度为630 s，并从30 s后对结构的疲劳损伤进行分析。图2 中概率密度柱状图中实线表示目标风压系数的概率密度函数，虚线表示与模拟风压系数相同均值和方差的高斯过程的概率密度函数。如图2 所示，模拟压力系数与目标压力系数的具有相同概率分布，表现出明显的非高斯特性。需要说明的是，角部分离区的偏斜系数和峰态系数分别是-0.79 和4.2，屋脊分离区的偏斜系数和峰态系数分别是-0.72和3.8，角部再附区的偏斜系数和峰态系数分别是-0.92 和4.97，屋脊再附区的偏斜系数和峰态系数分别是-0.74 和3.98。图3 比较了目标谱与风压系数时程的模拟谱，结果表明不同位置处压力系数功率谱密度较好的吻合了目标谱。

图 3 模拟的非高斯时程功率谱与目标谱比较Fig.3 Comparison of target spectrum and PSDs of simulated non-Gaussian time histories

将平均风速从1 m/s～21 m/s 范围内，每隔2 m/s为一个风速单元，计算该风速单元内的疲劳损伤，并考虑平均风速的概率密度函数，根据式(16)和式(17)得到给定平均风速考虑金属屋面板结构参数不确定条件下的疲劳损伤和疲劳寿命区间。

图4 所示为采用能量密度法[24]，根据北京气象塔实测风速数据[25]，统计得到北京地区城市地貌年平均风速两参数Weibull 分布。如图所示，采用能量密度法准确得到平均风速的概率密度函数，并以该平均风速概率密度函数作为本文计算金属屋盖风致疲劳的平均风速概率密度函数。

图 4 实测数据[21]与Weibull 平均风速模型对比Fig.4 Comparison of probability density of mean wind speed by Weibull distribution and measured data

5 算例

本文数值算例均采用Matlab R2014a 程序编写，结构整体矩阵及验证参见文献[26 - 27]。图5为考虑参数不确定金属屋面板在风荷载作用下疲劳损伤/寿命的计算程序流程图，可按步骤编写计算程序。

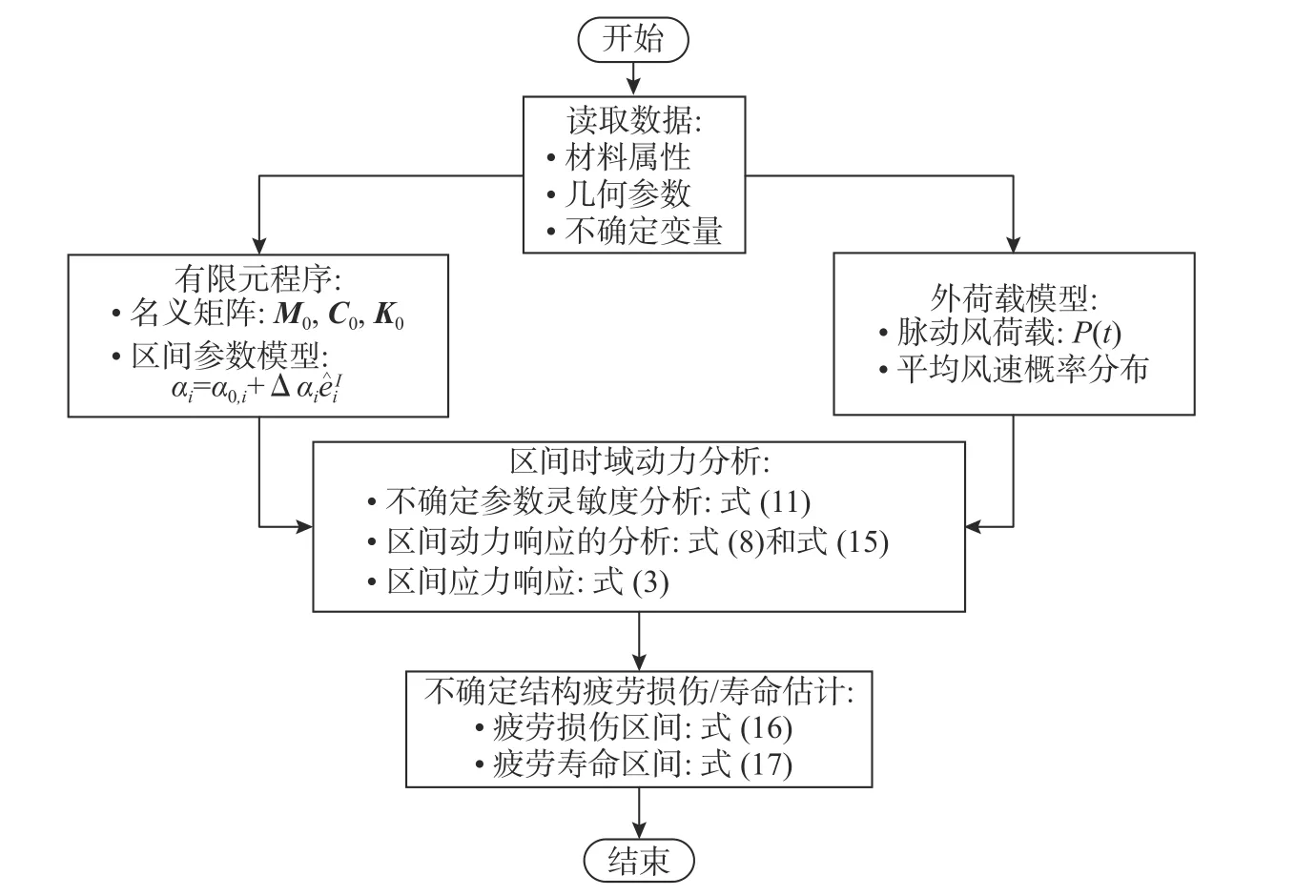
图 5 金属屋面板疲劳损伤区间分析方法计算程序流程图Fig.5 Flow-chart of interval analysis method of time domain fatigue evaluation

将本文所述区间疲劳分析理论应用于金属屋面板风致疲劳计算中，材料参数和屋面板尺寸均按照《压型金属板工程应用技术规范》[28]中铝合金材料取值，弹性模量、泊松比、板厚和密度分别为7.0×1010Pa、0.3、0.6 mm 和2.7×103kg/m3；采用四边形单元建模，取0.8 m×4.0 m 大小屋面板[27]，短边固支、长边简支，屋面板在x 方向、y 方向上分别均分20 和4 等分，共划分80 个单元，如图6所示；铝合金材料的S-N 曲线通过常规轴向拉伸试验方法获得[29]：

式中：N 为发生疲劳破坏时循环荷载的次数；S/MPa 为应力幅。

图 6 屋面板几何尺寸和计算点示意图 /mm Fig.6 Geometry size and calculation point

考虑弹性模量和板厚是结构不确定参数两种不同情况，且不确定性大小分别为5%、10%和20%。将不同区域风荷载分别作用于金属屋面板，通过根据式(8)分析计算得到屋面板响应挠度的区间时程，由式(2)和式(3)得到应力响应。

图7 分别表示考虑5%板厚不确定情况下，金属屋面板分离区角部、分离区屋脊和再附区角部、再附区屋脊在脉动风荷载作用下的金属屋面板中心位置的Mise 等效应力响应。右侧直方图表示名义应力的概率密度，点线和实线分别表示应力上界和下界的概率密度。如图所示，如果仅按结构名义值进行计算将会过高估计结构的实际情况，不能满足结构设计要求。需要强调的是，本文采用的区间动力响应分析方法仅需一次动力响应分析就可得到参数不确定结构的动力响应区间，而顶点法需要对不确定参数进行组合后，再进行动力响应分析，并从计算结果中选取动力分析的极大值和极小值。就本例而言，当定义金属屋面板的板厚为不确定参数，且不同单元的板厚不相关，采用顶点法需要通过280动力响应分析才能得到金属屋面板在脉动风荷载作用下的动力响应区间，而本文方法仅需一次动力响应分析，大幅减少了计算量。

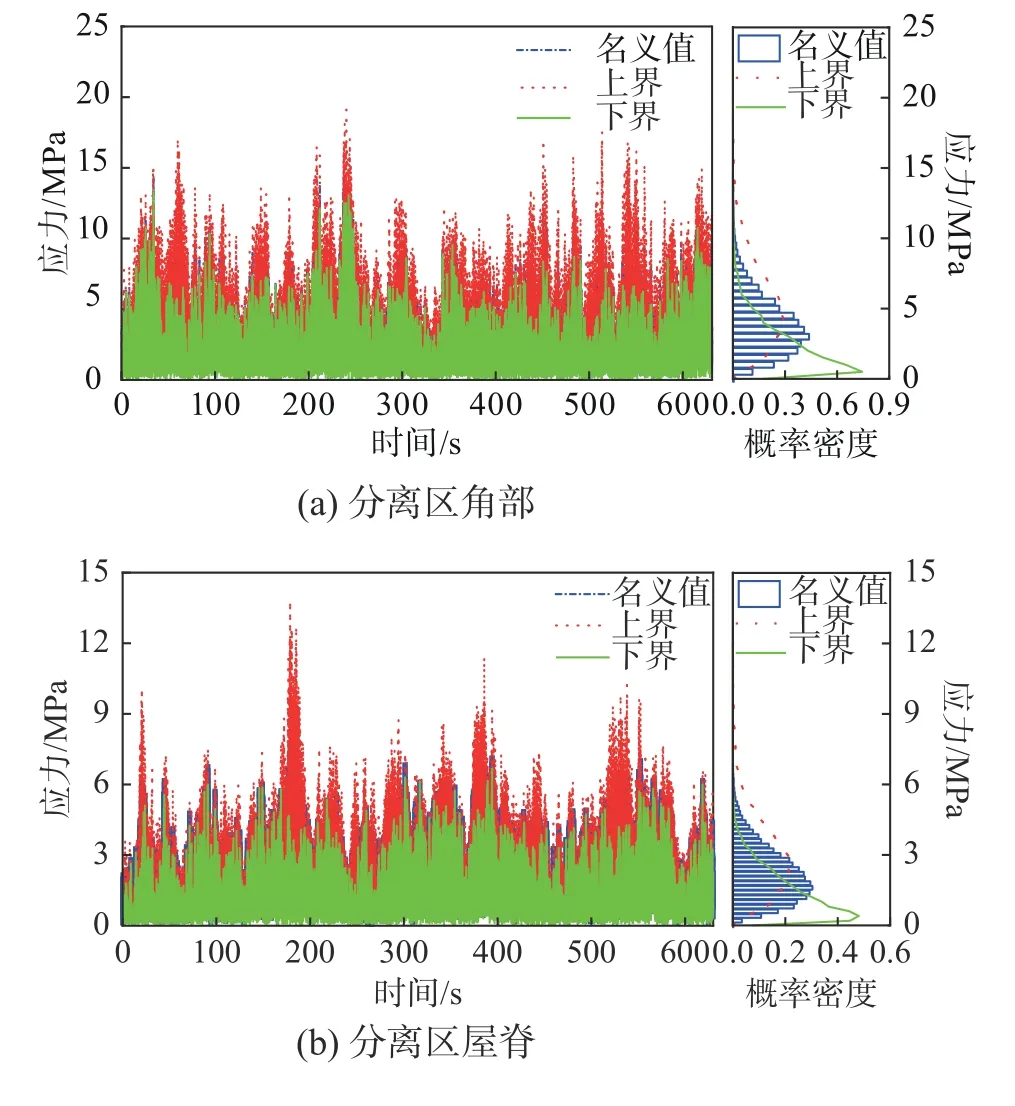
图 7 5%板厚不确定情况下屋面板的动力响应时程Fig.7 Dynamic response time history analysis under 5%uncertainty of elastic modulus

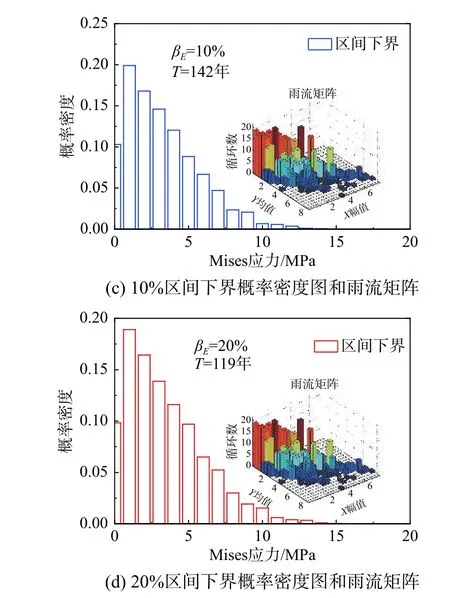
图 8 疲劳寿命关于弹性模量灵敏度分析Fig.8 Comparison of fatigue life by sensitivity of elastic modulus

图8 和图9 分别是定义弹性模量和屋面板厚度是不确定参数情况下，采用式(17)计算得到屋面板分离区角部中心处的疲劳寿命下界。当不考虑结构不确定时，分离区角部屋面板的疲劳寿命为159 年。考虑金属屋面板由于施工等因素引起弹性模量或板厚在一定范围内不确定时，屋面板的疲劳寿命随结构参数的不确定区间增大而降低；当金属屋面板材料的弹性模量和板厚在20%范围内不确定时，屋面板中心处的疲劳寿命分别下降至119 和22 年。需要说明的是，受安装误差、温度等引起的内力重分布等因素影响，结构在施工和实际使用过程中情况将更为复杂。

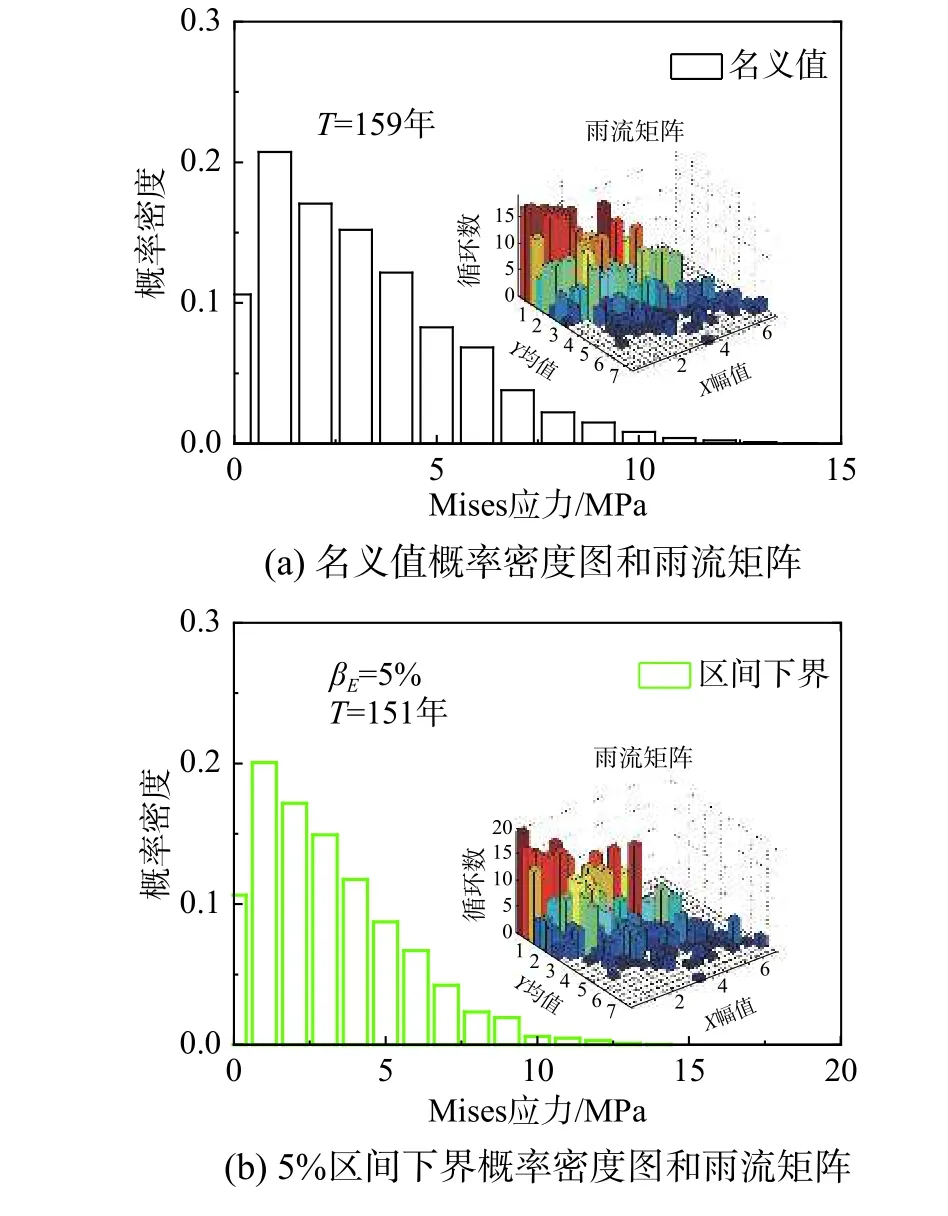
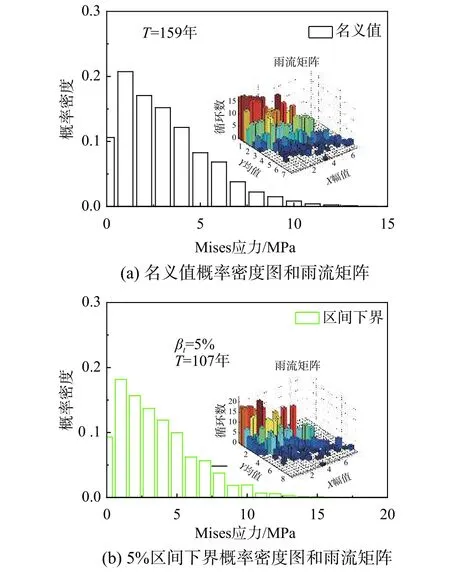
图 9 疲劳寿命关于板厚灵敏度分析Fig.9 Comparison of fatigue life by sensitivity of thickness

图10 通过调节式(8)中单位对称区间，比较了弹性模量和板厚的不确定性对金属屋面板风致疲劳寿命的影响。由于材料的S-N 曲线是高次非线性方程，因此金属屋面板的疲劳寿命区间下界随弹性模量和屋面板板厚降低而降低。同时，屋面板的弯曲刚度与板厚是三次立方关系，屋面板板厚的不确定性对屋盖结构的疲劳寿命有较大影响。需要强调的是，本文方法仅通过一次动力响应分析即可计算结构的疲劳损伤/寿命的界限，大幅减少了计算量。

图 10 疲劳寿命关于弹性模量和板厚灵敏度分析Fig.10 Comparison of fatigue life by sensitivity of elastic modulus and thickness

6 结论

在时域疲劳分析方法的基础上，采用区间参数模型定义结构参数的不确定性，提出考虑由于施工误差等因素引起的结构不确定条件下金属屋面板在脉动风荷载作用下的疲劳损伤/寿命估计方法。本文方法具有以下特点：

(1) 在时域疲劳分析方法的基础上，采用区间参数模型定义金属屋面板的不确定参数，考虑施工误差等因素对屋面板疲劳损伤/寿命的影响；

(2) 在疲劳损伤估计中对不确定参数进行组合，仅需一次动力响应分析即可计算金属屋面板的疲劳损伤/寿命的界限，避免了顶点法需要多次动力响应分析；

(3) 与频域疲劳区间分析方法相同，可通过调节不确定参数的单位对称区间，实现同一参数不同不确定半径疲劳损伤/寿命的近似计算。

数值算例表明：如果考虑结构不确定性，则结构的疲劳寿命率将大幅降低；因此对于重要结构，需要在疲劳分析中考虑结构的不确定性。同时，与传统的确定性方法和概率方法不同，区间理论得出的并不是结构疲劳寿命的准确值，而是根据结构的不确定性大小给出合理的疲劳寿命区间，当结构到达疲劳寿命区间下界时，结构就有可能发生疲劳破坏，需要及时对结构采取检修或加固等维护措施。