工字形钢筋混凝土矮墙抗剪承载力研究
马佳星,陈柯宇,王银辉,李 兵
(1. 浙大宁波理工学院土木建筑工程学院,浙江,宁波 315100;2. 浙江理工大学建筑工程学院,浙江,杭州 310018;3. 新加坡南洋理工大学土木与环境工程学院,新加坡 639798)
剪跨比小于或等于2 的钢筋混凝土(Reinforced concrete)剪力墙被称为RC 低矮剪力墙(Squat wall or Short wall)[1-2]。根据截面形状,RC 低矮剪力墙(以下简称为RC 矮墙)可进一步分为矩形RC 矮墙和工字形RC 矮墙。其中,工字形RC 矮墙在双主轴向均具有较高的强度和刚度,故常作为抵抗因地震产生的双向弯矩的主要构件,被广泛运用于抗震建筑,特别是核电站设施中[3-4]。同时,由于其自身的几何特性,工字形RC 矮墙能够满足住宅空间等建筑需求,增大采光空间,故亦被用于低、多层房屋建筑中[5]。

现有设计规范主要建立在对于矩形RC 长墙的研究基础之上,并不适用于工字形RC 矮墙[10-11]。我国的《高层建筑混凝土结构技术规程》(JGJ3-2010)(高规)[12]中关于抗剪承载力公式尚未对不同截面形状的剪力墙进行有效区别。美国ACI 318-14规范中也未包含剪跨比对于抗剪承载力的影响。针对这一问题,各国学者从多角度进行了研究。陈晓磊等[13]改进了Hwang 等[14]提出的拉压杆模型,使之适用于RC 矮墙的力-位移全过程的计算。但此方式并不适用于带翼缘的RC 矮墙。Gulec等[15]及Kassem[16]均采用非线性回归的方法获取其针对工字形RC 矮墙的抗剪承载力公式。分析发现,前者提出的公式高估了工字形RC 矮墙的抗剪承载力。原因在于其认为翼缘中所有纵筋在抵抗剪力中均发挥作用,这与试验中观测到的剪力滞后现象相违背。后者提出公式的缺陷在于其并未考虑翼缘中纵筋对于抗剪承载力的贡献。鲁懿虬等[17]基于带端柱或翼缘的RC 剪力墙数据库对高规中相应公式进行了优化调整。但其计算精度仍待进一步提升。
本文建立了一个包含有152 个试件的工字形RC矮墙的试验数据库。对库中的数据进行统计整理分类后,评估了我国高规JGJ3-2010[12]、美国ACI 318-14[18]和ASCE 43-05 规范[19]、欧洲Eurocode 8[20]、新西兰NZS3101-2006 规范[21]在预测工字形RC矮墙抗剪承载力上的表现。同时,基于腹板裂纹分布,建立了考虑翼缘影响的抗剪承载力计算模型,并利用力平衡推导出相应公式。
1 规范中抗剪承载力计算方法
我国的《高层建筑混凝土结构技术规程》(JGJ3-2010)[12]第7.2.10 节中规定,偏心受压剪力墙的承载力( Vn1),在永久或短暂状况时,应满足:
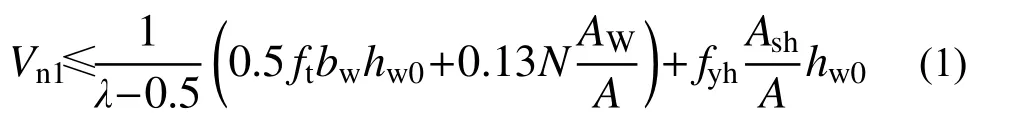
在地震设计状况时满足:

式中:γRE为承载力抗震调整系数,γRE≤1 ; N为剪力墙截面轴向压力设计值, N>0.2fcbwhw时,应取0.2fcbwhw; A为剪力墙全截面面积; Aw为剪力墙腹板截面面积; Ash、 s分别为同一截面内箍筋钢筋面积之和及箍筋钢筋间距; ft为混凝土抗拉强度; fyh为箍筋屈服强度;hw0为剪力墙截面有效高度; bw为剪力墙截面厚度; λ为计算截面剪跨比,λ<1.5 时应取1.5, λ>2.2 时应取2.2。计算截面与墙底之间的距离小于0.5hw0时, λ应按距墙底0.5hw0处的弯矩与剪力计算。
美国ACI 318-14 规范第18.10 节[18]中对抗震设计时剪力墙的抗剪承载力( Vn2)作出了规定,该公式是基于Wood[22]提出的桁架模型:
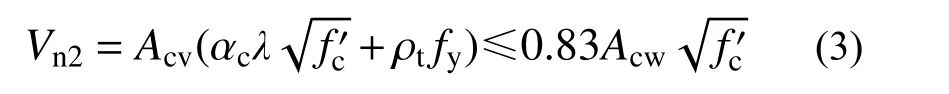
式中: Acv为受腹板厚度和截面长度约束的混凝土截面总面积; αc为调整系数,当hw/lw≤1.5时取0.25,当hw/lw≥2.0时取0.17,中间数采用插值计算; λ为混凝土重量调整系数,普通混凝土取1;ρt为水平钢筋配筋率; fy为钢筋屈服强度;Acw为墙肢截面面积; fc′为混凝土抗压强度。
美国ASCE 43-05 规范[19]中关于剪力墙抗剪承载力( Vn3)的规定与Barda 等[23]提出的方程有较多相似,相较于美国ACI 318-14 规范,包含了剪跨比、轴力等的影响[15],如式(4)和式(5)所示:

式中: Φ为抗力折减系数,一般取0.8; d为混凝土受压区边缘到受拉钢筋合力的作用点的距离,在缺少应变分析时可取0.6 lw; tn为墙厚度; fc′为混凝土抗压强度; hw为墙高; lw为墙长; NA为轴向荷载; ρse为组合配筋率, fy为钢筋屈服强度;A 和 B是与剪跨比有关的常数; ρh为水平钢筋配筋率; ρv为纵向钢筋配筋率。
欧洲Eurocode 8 规范[20]中规定,斜压破坏时剪力墙抗剪承载力( Vn4)为:

式中:αcw为考虑压杆应力状态的系数; tw为腹板的宽度;z 为内力臂,取0.8 lw( lw为墙长); fcd为混凝土抗压强度设计值,取fck/1.5 ; ν1为受剪混凝土的强度折减系数,取0.6(1.0-fck/250) ;fck为混凝土28 d 抗压强度; θ为混凝土斜压杆和垂直于剪力的墙轴的角度。
新西兰NZS3101-2006 规范[21]中规定的剪力墙抗剪承载力( Vn5)计算方式与美国ACI 318-14 规范第11.5 节相似,取式(7)和式(8)中计算值的较小者:

2 数据库

图1 对数据库中加载方式、截面尺寸、剪跨比、混凝土抗压强度、腹板纵筋屈服强度和水平钢筋屈服强度、翼缘纵筋屈服强度、腹板纵筋配筋率、水平配筋率和翼缘纵筋配筋率、轴压、抗剪承载力进行了分类展示。其中,试件墙长度范围为430 mm~3075 mm;腹板厚度不超过1000 mm的试件约占49.3%;墙高范围为145 mm~2200 mm,多小于1000 mm;腹板厚度范围为16 mm~150 mm,多集中在100 mm 左右;翼缘长度分布在145 mm~3045 mm,厚度分布在30 mm~150 mm;试件剪跨比小于1 的约占71.7%。从试件尺寸来看,大多数剪力墙都不是全尺寸墙。过往试验中,具有长翼缘的剪力墙数量相对较少。为了最大限度地减小尺寸效应的影响,同时考虑翼缘对剪力墙的影响,需要对具有较长翼缘的足尺剪力墙展开研究。
工字形RC 矮墙试验的加载方式多以拟静力循环加载为主。混凝土抗压强度在13.8 MPa~110.7 MPa,超过一半试件的混凝土抗压强度在33.2 MPa以下;腹板纵筋屈服强度在235 MPa~638 MPa,其中396 MPa~477 MPa 范围内的试件较多;腹板水平钢筋屈服强度范围与纵筋相近,但在460 MPa~535 MPa 区间内分布较少;翼缘纵筋屈服强度超过396 MPa 的试件约占总试件的71.1%。从材料角度看,数据库中大多数剪力墙选用普通硅酸盐混凝土制备。2000 年前测试了剪力墙试件的材料的强度较近年测试的试件低,腹板纵筋和水平钢筋配筋率多集中在0.3%~1.0%;与腹板纵筋配筋率相比,多数墙体的翼缘纵筋配筋率值较大,但在2.75%~4.0%范围内鲜有分布;轴压比范围为0~0.42,其中大多数剪力墙的轴压比范围集中在0.1 以下,表明矮墙所受轴压比较剪跨比较大的长墙而言较低。试件抗剪承载力在17 kN~7060 kN,多数墙体的抗剪承载力低于1500 kN。此外,在破坏模式上,大多数试件呈斜压破坏。因水平钢筋配置充足,鲜有斜拉破坏出现。少量试件因剪跨比接近2.0 或翼缘长度较短而呈现弯剪破坏模式,如Maier 等[26]、Mo 等[29]和韩小雷等[39]测试的部分试件。
3 规范公式评估
表1 展示了各国规范公式对于数据库中试件抗剪承载力计算值(Vcal)与实测值(Vpeak)之间的对比。分析数据包括平均值、中位数、标准差、变异系数、最小值、最大值和超出均值数占比。图2对比了各规范抗剪承载力的计算值与实测值。
从表1 可以看出,现有公式对工字形RC 矮墙的抗剪承载力均存在一定程度的低估。从数据上来看,欧洲Eurocode 8 规范[20]的计算结果相对比较准确。但该公式只考虑了腹板对于抗剪承载力的贡献。美国ACI 318-14[18]及美国ASCE 43-05 规范[19]的表现次之。其中,美国ACI 318-14 规范[18]亦未包含翼缘的影响,且并未包含轴压及腹板纵筋等参数的影响。前者已多次被证明能显著影响剪力墙的抗剪承载力。对于后者,Lefas 等[40]曾指出,在小剪跨比剪力墙中,腹板纵筋较水平钢筋而言对于抗剪承载力的贡献更大。美国ASCE 43-05规范[19]包括了轴压及腹板纵筋的贡献。Gulec等[15]发现,当运用此规范预测矩形RC 矮墙抗剪承载力时,计算值较实测值偏大30%左右。所以,尽管此规范亦未考虑翼缘的影响,其对于工字形RC 矮墙的抗剪承载力的预测偏差并不很大。新西兰NZS3101-2006[21]与美国ACI 318-14 规范第11.5 节[18]中公式相似,也只考虑了水平钢筋对于抗剪承载力的贡献。我国高规[12]计算结果的低估程度及离散程度均较高。原因在于其并未考虑翼缘中钢筋及混凝土的影响,未考虑腹板纵筋的影响,且低估的剪跨比的影响。
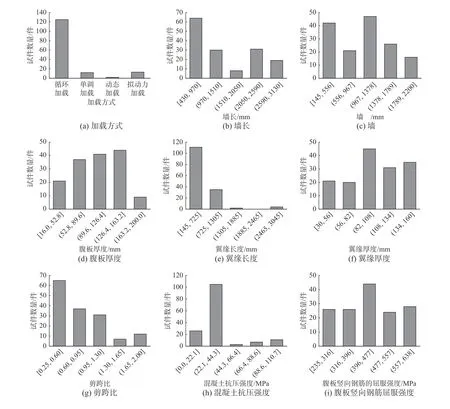
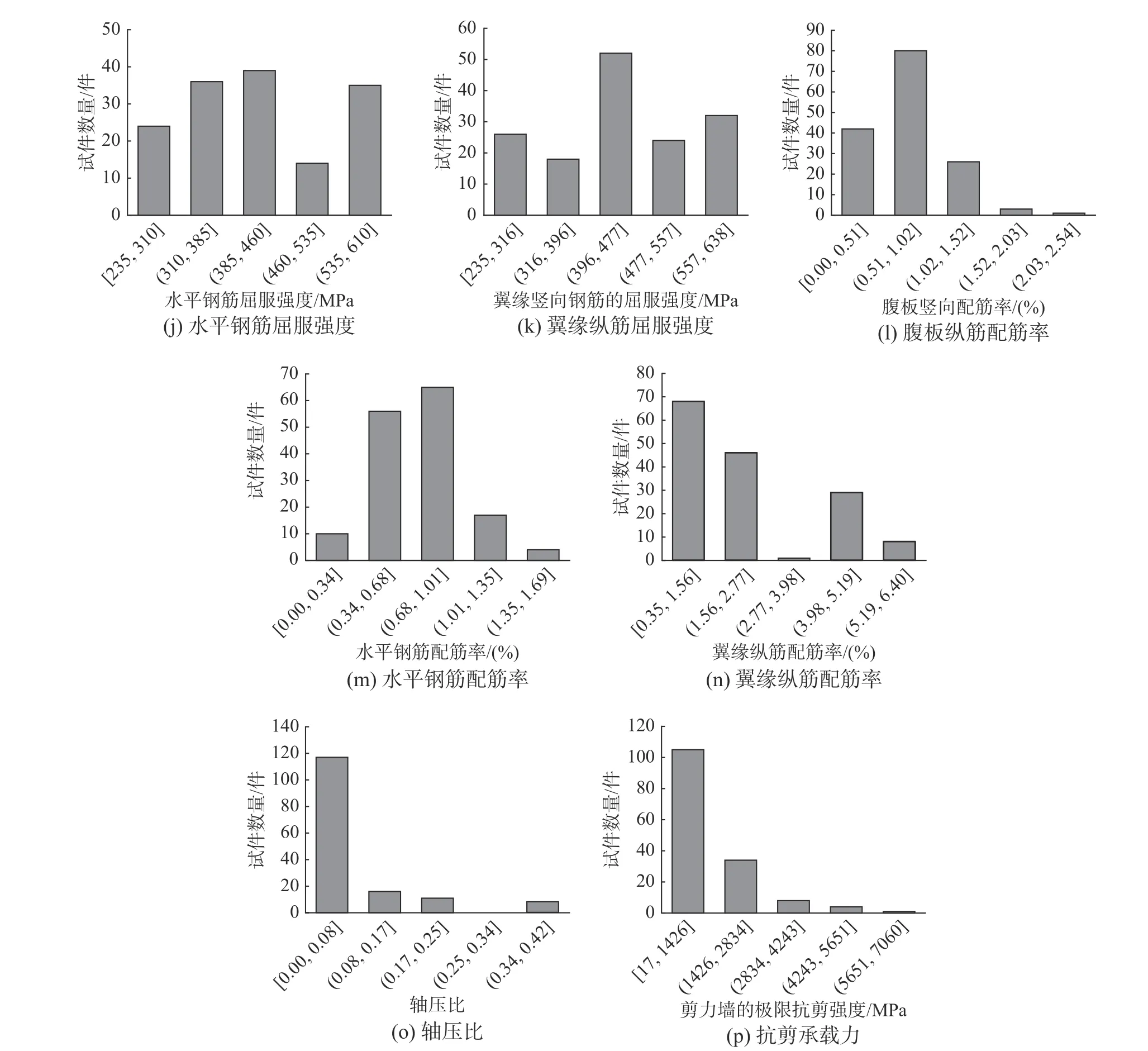
图 1 各参数分布情况Fig.1 Distribution of parameters
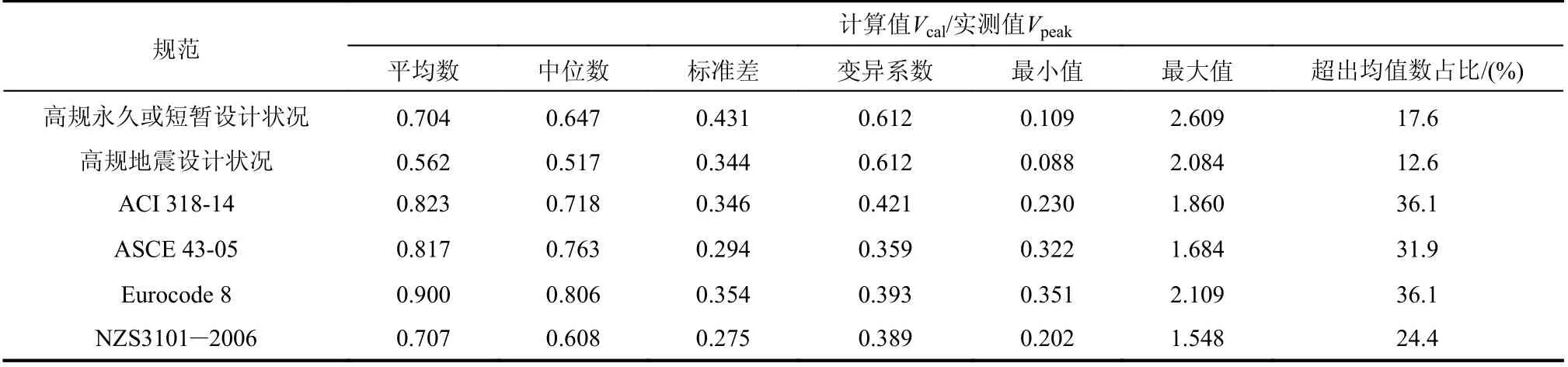
表 1 各规范抗剪承载力计算值与实测值对比Table 1 Comparison between calculated and measured values of shear strengths by building codes

图 2 不同剪跨比下抗剪承载力Fig.2 Shear strength of various shear span ratios
通过以上分析可以看出,现有规范不能精确预测工字形RC 矮墙的抗剪承载力,因其考虑参数不足及忽视了翼缘影响。且现有规范公式多为半经验公式,无法准确描述剪力墙内力传播过程。故需要从内力分析入手,提出针对于工字形RC 矮墙的抗剪承载力公式。
4 工字形RC 矮墙抗剪承载力公式
裂纹分布不仅反映了钢筋混凝土构件在地震后的破坏情况,同时能作为研究构件的内力传播的有效手段。Moehle[41]基于理想裂纹分布提出了一系列用于预测RC 矮墙抗剪承载力的公式。Luna 等[42]后利用12 片RC 矮墙的试验数据修正了该公式。通过上述数据库中剪力墙比对发现,当剪跨比小于1 时,现有规范对于工字形RC 矮墙抗剪承载力预测偏离较大。故本文拟采用类似手段,针对剪跨比小于1 的工字形RC 矮墙建立其抗剪承载力计算公式。
随着剪跨比的减小,剪力墙的破坏形态逐渐有弯曲破坏过度到剪切破坏。腹板斜裂纹亦呈现出由水平裂纹过度到斜向裂纹的趋势[37]。工字形RC 矮墙典型的裂纹分布如图3 可视。腹板斜裂缝将墙体分为了A、B、C 三部分。如图4 所示,每个部分都承受轴向应力 p 和剪切应力v ; θ为腹板裂纹相对于水平方向的角度; hw为墙高; lw为墙长; tw为腹板厚度; Fv和 Fh为腹板纵筋和水平钢筋所承受的力; Fs为沿斜裂纹的摩擦力;Fcx和Fcy为一侧受压混凝土反力的水平和垂直分量。
因此,腹板纵筋受力 Fv可表示为:

式中: k1为腹板纵筋的应力系数,取0~1; ρv为腹板纵筋配筋率; tw为腹板厚度; fyv为腹板纵筋屈服强度; hw为墙高;腹板水平钢筋受力由 Fh表示。由右下角A 点的力矩平衡可得:


图 3 工字形RC 矮墙理想裂纹分布Fig.3 Idealized cracking pattern of H-shaped flanged RC squat walls
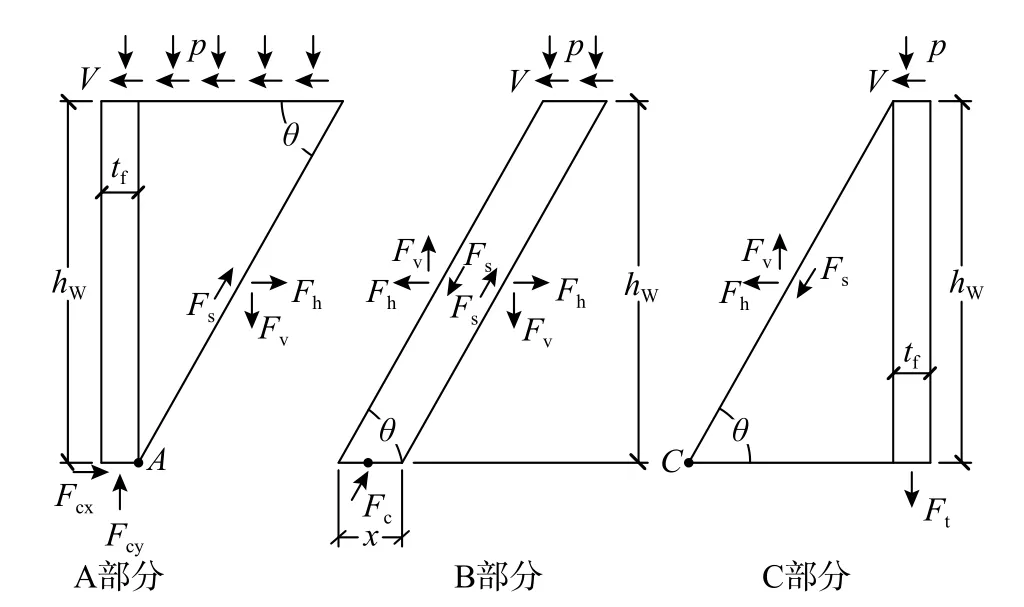
图 4 工字形RC 矮墙的自由体图Fig.4 Free body diagram of H-shaped flanged RC squat walls
因此,A 部分承受的剪力为:

B 部分进一步被划分为多个宽度为x 的单元体,其中 Fc为反作用力。由单元体底部中点的力矩平衡可得:
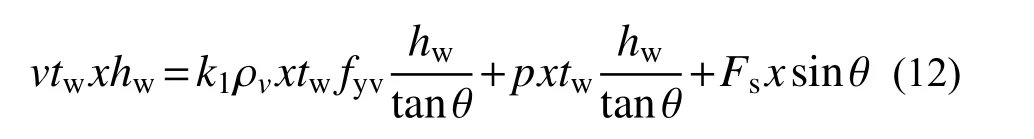
因此,B 部分承受的剪力为:
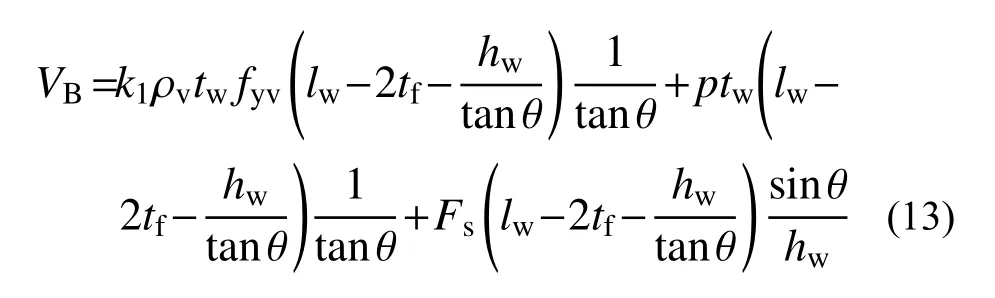
由于剪力滞后效应的存在,并不是所有翼缘纵筋都在最大抗剪承载力时达到屈服[43]。于是定义一个范围为0~1 的系数 k2描述翼缘纵筋的应力状况。

由C 部分左下角点的力矩平衡可得:

因此,C 部分承受的剪力为:

工字形RC 矮墙的抗剪承载力是上述A、B、C 三部分所承受的剪力之和:
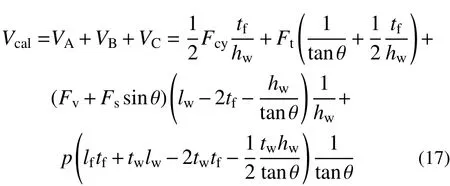
在上述方程式中,A 部分混凝土反作用力垂直分量 Fcy为:

摩擦力 Fs主要由裂缝间的骨料摩擦承担,其大小具有很大的不确定性[16]。在Moehle[41]和Luna等[42]学者提出的模型中,沿斜裂缝的正应力和剪应力均假定只由钢筋承担。这一假定并不影响所提出公式对于抗剪承载力的预测结果[44]。因而本文采用相同的假设,令摩擦力 Fs=0。故工字形RC 矮墙的抗剪承载力公式可进一步表示为:

获取抗剪承载力计算公式的基本形式后,需进一步决定参数 k1、 k2的取值。本文选用MATLAB中Fmincon 求解器进行非线性回归分析。此方法亦被Gulec 等[15]、Kassem 等[45]、徐亚丰等[46]学者采用。针对数据库中剪跨比小于1 的试件(包括Barda 等[23]、 Hirosawa[24]、Synge[25]、Saito 等[27]、Sato 等[28]、Mo 和Chan[29]、Naze 等[31]、Palermo 和Vecchio[32]、Ma 和 Li[37]、傅剑平等[38]、韩小雷等[39]的试件)进行求解可得k1=1 ,k2=0.92。同时,为表征典型的工字形RC 矮墙腹部斜裂纹同时对所得公式进行简化, θ取45°。因而:

利用本文提出的公式对数据库中试件进行抗剪承载力计算,结果如表2 和图5 所示。从数据上看,本文提出的公式能较好的预测工字形RC 矮墙抗剪承载力。但在图5 中发现1000 kN 左右的试件有一定差异,其原因在于部分试件会产生提前破坏,进而导致预测值比实测值提高。Ma 和Li[37]指出HP0D0 的试件(轴压比和侧向荷载与腹板夹角均接近0)在受压过程中出现提前破坏(premature failure),并没有达到设想中的抗剪承载力,造成这一现象的原因与力的传输机制有关。同样的结果在Palermo 和Vecchio[32]也有提及,他们认为腹板采用较弱的混凝土和薄壁截面的性质会导致提前破坏的出现。但总体上,通过表2 可知,预测公式计算值与实测值之比的均值为1,变异系数较其余规范也较小。

表 2 本文预测公式计算值与实测值对比Table 2 Comparison of calculated and measured values in this paper

图 5 推导公式抗剪承载力计算值与实测值的比较Fig.5 Comparison between calculated and measured shear strengths
从机理上看,本文提出的公式乃建立于对工字形RC 矮墙内力传播分析基础之上,并能较好地反映翼缘钢筋和混凝土的贡献,且同时考虑了混凝土抗压强度、轴向荷载和墙高等重要参数的影响。故该公式可用于指导剪力墙的抗震设计。
5 结论
本文建立了一个参数详尽的工字形RC 矮墙试验数据库。比较分析了我国高规JGJ3-2010[12]、美国ACI 318-14[18]和美国ASCE 43-05 规范[19]、欧洲Eurocode 8 规范[20],新西兰NZS3101-2006 规范[21]对于数据库内试件抗剪承载力的预测效果。而后,通过腹板斜裂纹分布,提出了描述工字形RC 矮墙内力传播的自由体图。在此基础上,推导出工字形RC 矮墙的抗剪承载力计算公式的基本形式。并进一步利用非线性回归分析确定相关系数取值。主要结论如下:
(1)本文建立了一个包含152 个试件的工字形RC 矮墙试验数据库,详尽记录了墙长、墙高、腹板厚度、翼缘长度、翼缘厚度、剪跨比、混凝土抗压强度、腹板纵筋屈服强度、水平钢筋屈服强度、翼缘纵筋屈服强度、腹板纵筋配筋率、水平钢筋配筋率和翼缘纵筋配筋率、轴压、抗剪承载力这15 个重要参数。并将上述数据以图表形式展现。
(2)现阶段各国规范在工字形RC 剪力墙抗剪承载力的预测上均存在不同程度的缺陷。主要原因包括考虑参数不足、未妥善考虑翼缘中钢筋及混凝土的影响等。
(3)本文针对剪跨比小于1 的工字形RC 矮墙,基于腹板裂纹分布,建立了考虑翼缘影响的抗剪承载力计算模型。并利用力平衡推导出抗剪承载力计算公式。与各国规范相比,本文提出的公式预测精度更高,所得计算值与实测值之比的均值为1,变异系数也较小。该公式可为剪力墙的抗震设计及规范公式的修订提供指导。

