圆局部竞赛图的最小控制集
张新鸿,薛彩娟
(太原科技大学 应用科学学院,山西 太原 030024)
0 引言
1962年,Ore提出了图的控制集这一概念[1],近年来,越来越多的学者们对控制集进行了研究,图的控制理论得到迅速的发展,并广泛应用于通信网络、信息学等多方面,相关结论可以参看文献[2-9]。
设D是一个具有n个顶点的有向图,常记为D=(V,A),其中V和A分别表示有向图D的顶点集和弧集。有向图控制集的研究可参看文献[10-13]。有向图D的阶表示D中顶点的数目,记为|D|。如果uv是一条弧,那么称u控制v(或v被u控制),记为u→v。对于V(D)中不交的顶点子集X和Y,X→Y表示X中的每一个顶点控制Y中的每一个顶点。定义

即(Y,X)D表示尾在Y中,头在X中的弧集。X⇒Y表示(Y,X)D=∅。X↦Y表示X→Y和X⇒Y同时成立。给定有向图D=(V,A),对于顶点集T⊆V(D),如果对每个顶点v∈V(D)T,至少存在一个顶点t∈T,使得tv∈A(D),那么称T是有向图D的一个控制集[14],其中所含顶点个数最少的控制集称为D的最小控制集。
设v∈V(D),定义集合,分别称集合和为顶点v的外邻集和内邻集。是以v为尾的所有弧的数目,称为顶点v的外度是以v为头的所有弧的数目,称为顶点v的内度。设V(H)⊆V(D),A(H)⊆A(D),如果两个端点都在V(H)中的每一条弧都属于A(H),则称H是由X=V(H)导出的,记为,也称H为D的一个导出子图。如果对于D的每一对不同的顶点x和y,总存在一条(x,y)途径和(y,x)途径,那么称有向图D是强连通的。
无2圈的有向图称为定向图,任意两个顶点均相邻的定向图称为竞赛图。定向图以及竞赛图的相关研究参看文献[15-16]。每一对不同的顶点都相邻的简单图称为无向完全图[17]。无向完全图的双定向图称为半完全有向图。有向图D是局部内半完全的(局部外半完全的),如果对于D的每一个顶点x,它的全体内邻点(外邻点)诱导出一个半完全有向图。如果有向图D既是局部内半完全有向图,又是局部外半完全有向图,那么称D是局部半完全有向图。局部半完全有向图的相关研究可参看文献[18]。一个无2圈的局部半完全有向图称为局部竞赛图。局部竞赛图中除竞赛图以外的图称为纯粹局部竞赛图。
给定一个n阶有向图D,如果它的顶点可标号为v1,v2,…,vn,使得对每一个i∈ {1,2 ,…,n} ,
和
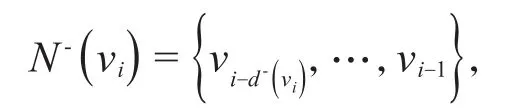
那么称D是一个圆有向图,称顶点序v1,v2,…,vn是D的一个圆标号,其中所有的下标均是模n的。圆有向图的相关研究参看文献[19]。
定理1[20]每一个圆有向图都是局部半完全的。
由定理1可知,圆有向图属于局部半完全有向图。根据是否为竞赛图,可将圆的局部竞赛图分为圆的纯粹局部竞赛图和圆竞赛图两类。本文通过对圆的纯粹局部竞赛图、圆竞赛图的研究,完全刻画了圆局部竞赛图的最小控制集。
1 圆的纯粹局部竞赛图的最小控制集
1.1 非强连通圆的纯粹局部竞赛图的最小控制集
为叙述方便,我们进行如下定义。设D是一个有向图,P=v1…vn是D的一条有向路。如果存在弧vsvr∈A(D)满足r-s≥2(s,r∈ {1,2,…,n}),则称弧vsvr为路P的一条跨弧,并且称|r-s|为弧vsvr的跨度。如果在路P上不存在跨弧vsαvrα使得sα<s<r<rα,那么就称跨弧vsvr为路P上的一条极大跨弧。如果存在路P的一个跨弧集合H=满足:(1)|si+1-ri-1|≥2;(2)不存在极大跨弧vsmvrm使得si+1<sm≤ri<ri+1<rm;(3)si<si+1≤ri<ri+1,或者si<ri<si+1<ri+1且si+1-ri=1,那么称集合H为路P上的一个极大跨弧覆盖,称顶点集被H覆盖。设Pm是P的一条子路,如果Pm上的所有顶点均不被任何极大跨弧覆盖所覆盖,则称Pm为P的一条纯粹子路。若不存在vα∈V(P)使得是P的纯粹子路,则称Pm为P的一条极大纯粹子路,称V(Pm)中的所有顶点被Pm覆盖,如图1。

图1 {vs1vr1,vs2vr2}为P=v1v2...v19上的一个极大跨弧覆盖,{vs3vr3}是P上一个只含一条极大跨弧的极大跨弧覆盖Fig.1 {vs1vr1,vs2vr2}is a maximal cross arc onP=v1v2…v19,{v s 3vr3} is a maximal cross arc cover with one maximal cross arc on P
由非强连通性可知,顶点vn与v1之间不存在弧。由圆有向图的定义可知,必有vi→vi+1,其中,i∈{1,2,…,n-1},因此非强连通圆的纯粹局部竞赛图必存在一条哈密尔顿路。根据非强连通圆的纯粹局部竞赛图的结构,我们可以得到下面的结论。
引理1设非强连通圆的纯粹局部竞赛图D=v1v2…vn是一条路。当n=2k时,D的最小控制集为{vα|α=1,3,…,2k-1};当n=2k+1 时,D的最小控制集为
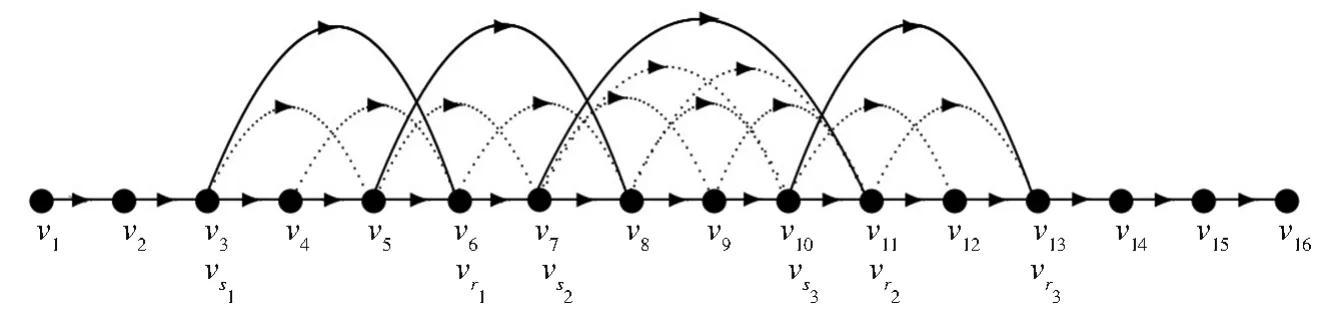
图2 一个16阶的非强连通圆的纯粹局部竞赛图D,{vs1vr1,vs2vr2,vs3vr3}构成了一个极大跨弧覆盖,vs3+m3是只能被极大跨弧vs3vr3覆盖的所有顶点中下标最小的顶点Fig.2 Around pure local tournamentDwithn=16which is non-strong ,{vs1vr1,vs2vr2,vs3vr3}form a maximal cross arc cover,vs3+m3is a vertex with the smallest subscript which is only covered by cross arcvs3vr3
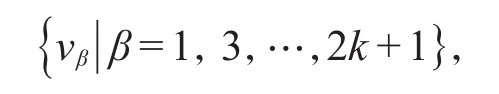
或

其中m∈ {1,3,5,…,2k-1},k∈Z+。
证明因为D是一条路,所以显然有vi→vi+1,1≤i≤n-1。
情形1n=2k。
设顶点集T={vα|α=1,3,…,2k-1}。首先证明T是D的最小控制集。由vi→vi+1可知,T是D的控制集,其中i∈{1,2,…,n-1}。任取顶点集T'={vi1,vi2,vi3,…,vi|T|-1}知|T'|=|T|-1。不妨设i1<i2<…<i|T|-1。(1)若∀t∈ {1,2,…,|T|-2},有|it+1-it|≤2,则由D是一条路可知,T'不能控制顶点vi|T|-1;(2)若∃t∈ {1,2,…,|T|-1},有it-it-1≥3,则由D是一条路可知,vit-1必不被顶点集T'控制。因此,D的最小控制集为T={vα|α=1,3,…,2k-1} 。再证唯一性。假设T1是D的一个最小控制集且T1≠T,则至少存在一个顶点vp∈TT1,其中p∈{1,3,…,2k-1}。 如果vp-1∈T1,那么由D是一条路及T1是D的最小控制集可知,T1不能控制vp+1;同理,如果vp+1∈T1,那么T1不能控制vp;如果{vp-1,vp+1}⊄T1,那么T1不能控制vp。故T是D唯一的最小控制集。
情形2n=2k+1。
取顶点集T={vβ|β=1,3,…,2k+1}或 {vβ|β=1,…,m-2,m,m+1,m+3,…,2k}。由

可知,T是D的控制集。由n=2k时的证明可同理得,此时T是D的最小控制集。
引理2设D是一个n阶非强连通圆的纯粹局部竞赛图,v1,v2,…,vn是D的一个圆标号。P=v1v2…vn是D的哈密尔顿路。如果路P上存在一个极大跨弧覆盖H={vsivri|i=1,2,…,t},那么,DV0的最小控制集为{vαi|i=1,2,…,t},其中αi∈ {si,si+1,…,si+mi}且vsi+mi是只能被vsivri覆盖的下标最小的顶点,Vo={vs1,vs1+1,…,vrt}。
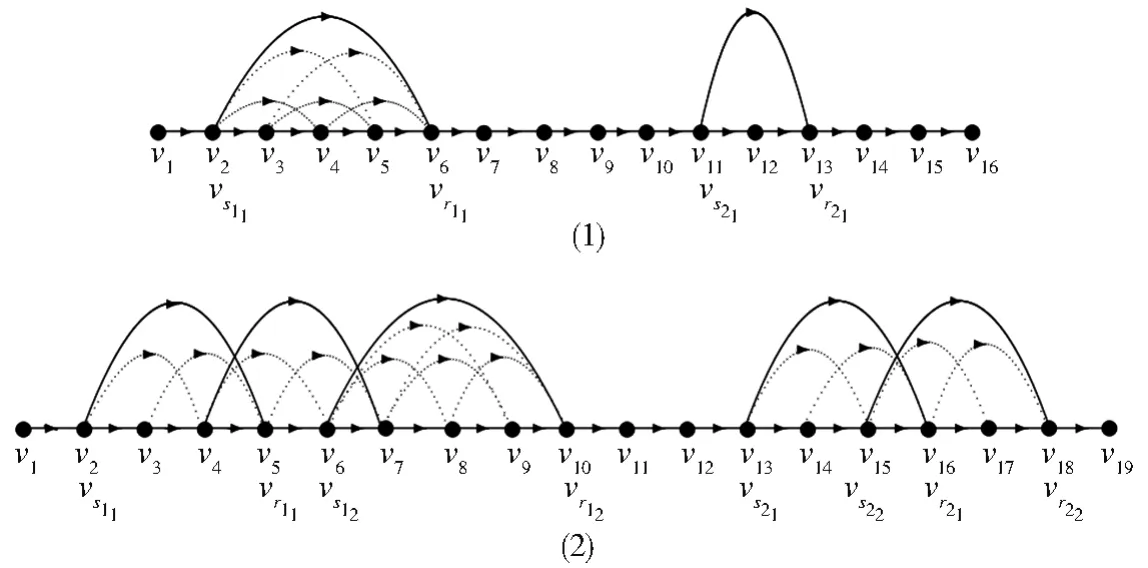
图3 (1)一个16阶的非强连通圆的纯粹局部竞赛图D,其中t1=1,t2=1;(2)一个19阶的非强连通圆的纯粹局部竞赛图D,其中t1=2,t2=2Fig.3 (1)Around pure local tournament withn=16 which is non-strong,t1=1,t2=1;(2)Around pure local tournament with n=19 which is non-strong,t1=2,t2=2



1.2 强连通圆的纯粹局部竞赛图的最小控制集
设D是一个强连通圆的纯粹局部竞赛图,v1,v2,…,vn是D的一个圆标号,所有下标均是模n的。设C是图D的一个长度至少为4的有向圈。连接圈上任意两个不相邻顶点的弧称为圈C的跨弧,即跨弧vsvr满足 |r-s|≥2(s,r∈{1,2,…,m}),称|r-s|为跨弧vsvr的跨度。设vsvr是圈C的一条跨弧,如果在圈C上不存在跨弧vsαvrα使得sα<s<r<rα(rα<r<s<sα),那么就称跨弧vsvr为圈C上的一条极大跨弧。如果存在圈C的一个跨弧集合H={vsivri|i=1,…,t}满足:(1)|si+1-ri-1|≥2,(2)不存在极大跨弧vsmvrm使得si+1<sm≤ri<ri+1<rm;(3)si<si+1≤ri<ri+1,或者si<ri<si+1<ri+1且si+1-ri=1,那么称集合H为圈C上的一个极大跨弧覆盖,称顶点集被H覆盖。设Pm是C的一条子路,如果Pm上的所有顶点均不被任何极大跨弧覆盖所覆盖,则称Pm为C的一条纯粹子路。若不存在vα∈V(C)使得是C的纯粹子路,则称Pm为C的一条极大纯粹子路,称Pm中的所有顶点被Pm覆盖。如图4。

图4 一个13阶的强连通圆的纯粹局部竞赛图D,其中{vs1vr1,vs2vr2}构成一个极大跨弧覆盖,v5v8不属于极大跨弧覆盖,P=v10v11v12v13v1是圈C的一条极大纯粹子路Fig.4 Around pure local tournamentD,{vs1vr1,vs2vr2}form a maximal cross arc cover,andv5v8is not included in a maximal cross arc cover,P=v10v11v12v13v1is a maximal purely subpath on cycleC
引理3设强连通圆的纯粹局部竞赛图D=v1v2...vnv1是一个圈。那么D的最小控制集为:当n=2k时,D的最小控制集为{vα|α=1,3,…,2k-1},或{vα|α=2,4,…,2k};当n=2k+1 时 ,D的最小控制集为

其中,k∈Z+,所有的下标均是模n的。
证明因为D是一个非强连通圆的局部竞赛图,且C=v1v2…vnv1是D的唯一哈密尔顿圈,所以有vi→vi+1,1≤i≤n-1。下面分两种情形证明结论成立。
情形1n=2k。
取顶点集T={vα|α=1,3,…,2k-1}。首先证明T是D的一个最小控制集。由vi→vi+1,1≤i≤n-1,可知,T是D的控制集。任取顶点集T'={vis|s=1,2,…,|T|-1},并且|T'|=|T|-1。不妨设i1<i2<…<i|T|-1。(1)若∀t∈ {2,…,|T|-1},有|it-it-1|≤2,则由D是一个哈密尔顿圈可知,T'不能控制顶点vi|T|-1;(2)若∃t∈ {1,2,…,|T|-1},有|it-it-1|≥3,则由D是一个哈密尔顿圈可知,T'不能控制vit-1。因此,由T'的任意性可知,T是D的一个最小控制集。再证唯一性。假设T1是D的一个最小控制集且T1≠T,则至少存在一个顶点vp∈TT1,其中p∈{1,3,…,2k-1} 或p∈{2,4,…,2k}。如果vp-1∈T1,那么由D是一个圈可知,T1不能控制vp+1;同理,如果vp+1∈T1,那么T1不能控制vp;如果{vp-1,vp+1}⊄T1,那么T1不能控制vp。故T是D唯一的最小控制集。
情形2n=2k+1。
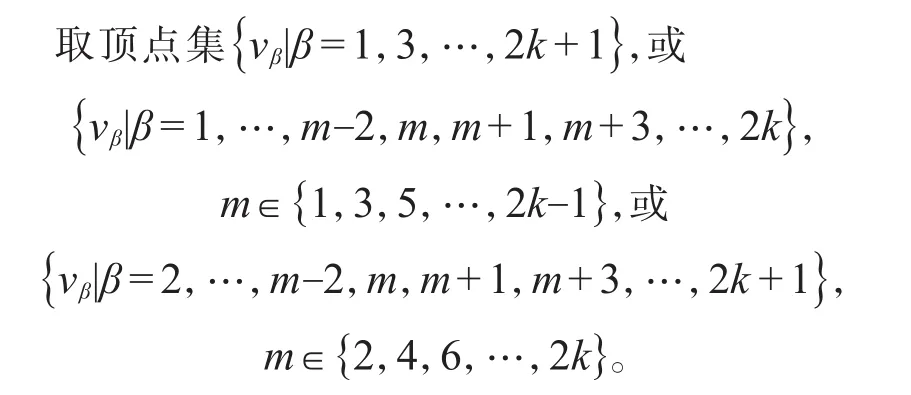
由vi→vi+1,1≤i≤n-1,可知,T是D的控制集。由n=2k时的证明可同理得,此时T是D的最小控制集。
引理4设D是一个n阶强连通圆的纯粹局部竞赛图,v1,…,vn是D的一个圆标号。C=v1…vnv1是D的一个哈密尔顿圈。如果圈C上存在一个极大跨弧覆盖,那么的最小控制集为,其中αi∈{si,si+1,…,si+mi}且vsi+mi是只能被vsivri覆盖的下标最小的顶点且所有的下标均是模n的,V0=。
证明首先证明是D最小控制集。因为所以由圆有向图的定义可知,由引理2可知,的控制集,令任取M⊆V0且|M|=t-1,则存在μ∈{1,…,t}使得Aμ∩M=∅。由H是一个极大跨弧覆盖可知,对任意的都有v不能控制vμ,其中vμ∈Aμ。又由于存在只被极大跨弧覆盖,故vγ不能控制,γ∈ {s1,s1+1,…,sμ-1}。因此,M不能控制。由M的任意性可知是的最小控制集(如图5)。设再证唯一性。任取顶点集,则至少存在一个顶点有
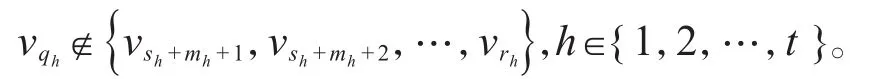
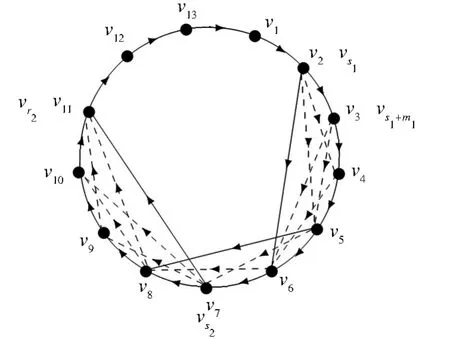
图5 一个13阶的强连通圆的纯粹局部竞赛图D,其中{v2v6,v7v11}构成一个极大跨弧覆盖,vs1+m1是只能被极大跨弧vs1vr1覆盖的所有顶点中下标最小的顶点Fig.5 Around pure local tournamentDwithn=13which is strong,{v2v6,v7v11}form a maximal cross arc cover,vs1+m1is a vertex with the smallest subscript which is only covered by cross arcvs1vr1
那么T0不能控制,所以的最小控制集为T。
定理3设D是一个n阶强连通圆的纯粹局部竞赛图,v1,v2,…,vn是D的 一个圆标号。C=v1v2…vnv1是D的哈密尔顿圈。如果圈C上存在h个极大跨弧覆盖
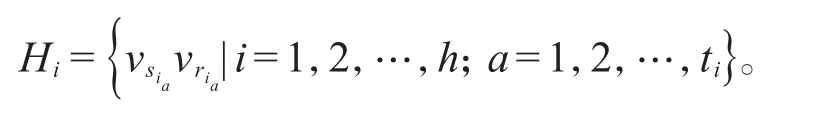
那么,D的最小控制集为
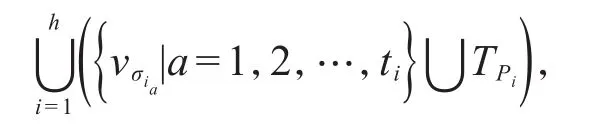


是D的最小控制集(如图6)。
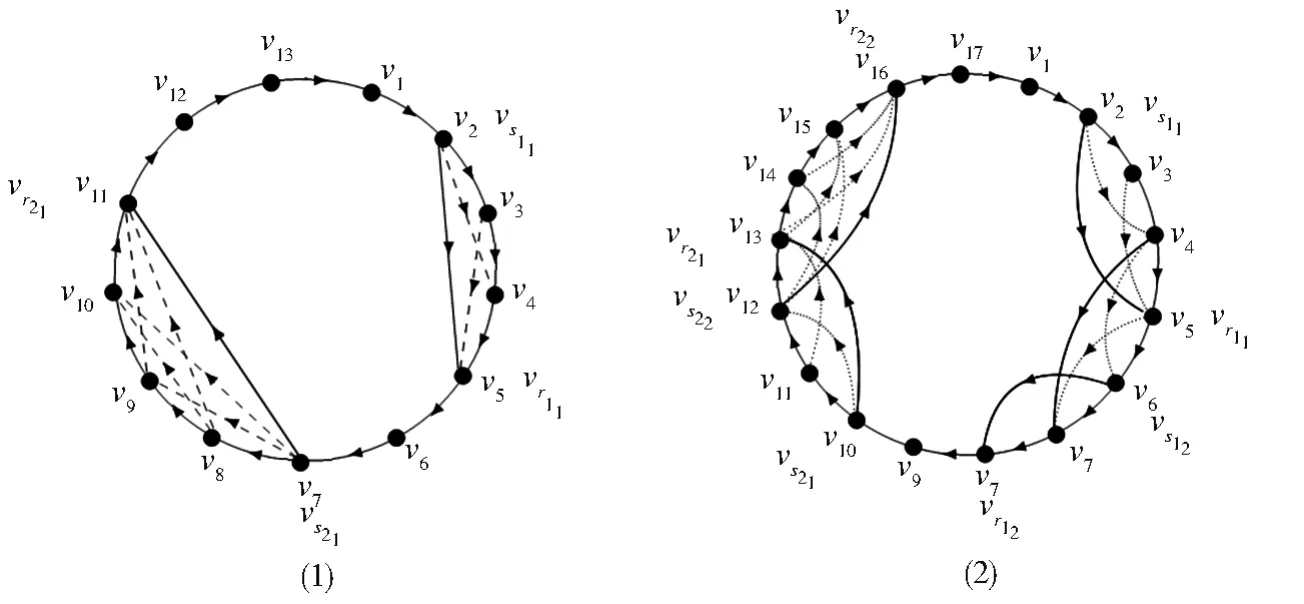
图6 (1)一个13阶的强连通圆的纯粹局部竞赛图D,其中v2v5,v7v11是两个只包含一条极大跨弧的跨弧覆盖;(2)一个17阶的强连通圆的纯粹局部竞赛图D,并且t1=2,t2=2Fig.6 (1)Around pure local tournamentDwithn=13which is strong,v2v5,v7v11are two cross arc cover with a maximal cross arc;(2)Around pure local tournamentDwithn=17which is strong,andt1=2,t2=2
再证唯一性。

2 圆竞赛图的最小控制集
引理5设D是一个n阶强连通圆竞赛图,v1,v2,…,vn是D的一个圆标号,则D的最小控制集为{vs,vr},其中vs,vr两个顶点满足vr=vs-d-(vs)或vs=vr-d-(vr),并且所有的下标均是模n的。
证明任取顶点vs∈V(D),因为D是圆竞赛图,所以vs不能控制vs-1,故vs不是圆竞赛图D的控制集。因此,圆竞赛图D的最小控制集至少包含两个顶点。由于D是强连通圆竞赛图,故存在一点vr→vs,不妨设vr=vs-d-(vs),则由强连通圆竞赛图的定 义 可 知 ,vs→ {vs+1, }vs+2,…,vr-1,vr→vs,因 此 ,{vs,vr}是D的控制集,所以,D的最小控制集包含两个顶点(如图7)。
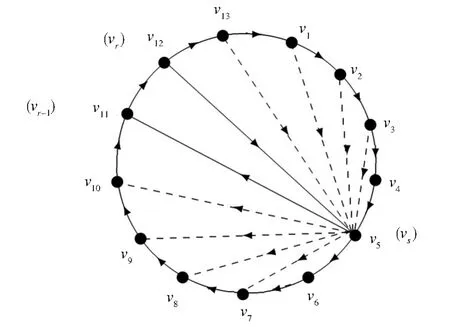
图7 一个13阶的强连通圆竞赛图DFig.7 A strong round tournamentDwithn=13
引理6设D是一个n阶强连通圆竞赛图,v1,v2,…,vn是D的一个圆标号,对任意的顶点vα∈V(D),必存在顶点vβ∈V(D),使得{vα,vβ}是D的一个最小控制集。
定理4设D是一个n阶强连通圆竞赛图,v1,v2,…,vn是D的一个圆标号,则D的最小控制集为其中,t∈{1,2,…,n},并且所有的下标均是模n的。
证明由D是一个强连通的竞赛图可知,|V(D)|≥3,并且对任取的vt∈V(D),都有d+(vt)≤n-2。下面分两种情形进行证明。如图8。
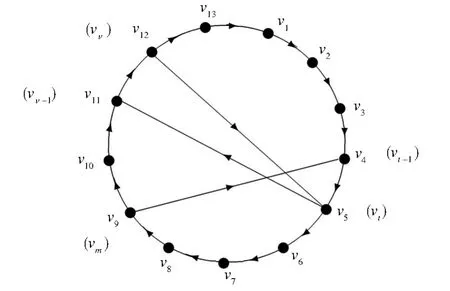
图8 一个13阶的强连通圆竞赛图DFig.8 Astrong round tournamentDwithn=13
情形 1d+(vt)<n-2,t∈ {1,2,…,n}。
因为D是强连通的,所以N-(vt)≠∅。又D是一个强连通的圆竞赛图,不妨设由D是圆的竞赛图可知,这样就有

若m=v,则。否则,有。任取顶点,易知
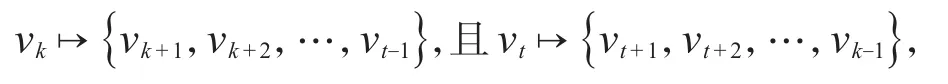
这样{vt,vk}是D的一个控制集。再由引理5可知,{vt,vk}是D的最小控制集。
情形 2d+(vt)=n-2,t∈ {1,2,...,n}。
由d+(vt)=n-2可知,d-(vt)=1。因此,N-(vt)={vt-1},即vt↦ {vt+1,vt+2,…,vt-2}。再由引理 5,立刻就有{vt,vt-1}构成D的一个最小控制集。又D是一个强连通的圆竞赛图,此时N-(vt-1)∩N+(vt)≠∅。任取vk∈ (N+(vt)∩N-(vt-1)),由情形1可知{vt,vk}构成D的一个最小控制集。
任取顶点vp∉(N+(vt)∩N-(vt-1))∪{vv}。 若vp∈ {vt+1,vt+2,…,vm-1},则由vm=vt-1-d-(vt-1)和强连通圆竞赛图的定义可知,vt和vp都不能控制vt-1,即{vt,vp}不是D的控制集。若vp∈ {vv+1,vv+2,…,vt-2},则由vv=vt-d-(vt)可 知 ,vv↦ {vv+1,vv+2,…,vt-1,vt},故{vt,vp}不能控制vv,即{vt,vp}不是D的控制集。因此,{vt,vk}是D的最小控制集,

其中,t∈{1,2,…,n}。
定理5设D是一个n阶非强连通的圆竞赛图,v1,v2,…,vn是D的一个圆标号,则D的最小控制集为{v1}。
证明由D是非强连通的圆竞赛图,得v1↦vi,i∈{2,3,…,n},故D的最小控制集为{v1}。

