实证资产定价研究中的t统计量比较与应用
蔺平爱,董晨昱,薛志诚
(山西大学 数学科学学院,山西 太原 030006)
0 引言
在实证资产定价的研究中,Fama和MacBeth[1]的横截面回归及Fama和French[2]的组合水平分析是最为常用的两个方法。当通过回归分析检验各因子(如:市场风险、规模、账面市值比、盈利价格比、流动性、动量、反转等)与股票预期收益的关系时,回归系数的显著性决定了问题的关键,Fama-MacBeth横截面回归共分为两步,第一步是在给定时间点上以股票为样本通过最小二乘法进行横截面回归,第二步则是求各系数序列在时间上的均值(作为最终的系数估计值)及相应的t统计量值。组合水平分析主要用于研究各因子是否有显著的溢价,其中,求各组合平均收益与求Fama-MacBeth估计的原理相同,同样分为两步进行,第一步是在每个时间点上将股票分组,并求组合下一期的平均收益,第二步则是在时间序列上求各组合平均收益的均值(即组合平均收益)及相应的t统计量值。
Fama-MacBeth横截面回归和组合水平分析都面临序列均值是否为0的检验。在实证资产定价的文献中,针对该检验的t统计量常见的有四种不同的形式。第一种是普通t统计量(估计值/标准差),对独立同分布序列,当原假设为真时,该统计量服从近似的t分布(当样本来自正态总体时,该分布是精确的t分布),李宏等[3]、Kahraman 等[4]、史代敏等[5]、陈淼鑫等[6]在其研究中均使用了普通t统计量;第二种是一阶自相关系数调整的t统计量,当序列存在自相关性时,由于标准差的估计不再具有相合性,使得普通t统计量有较低的效,为了提高检验的效,Fama等[7]及 Cooper等[8]在组合分析中使用了该统计量;第三种是White[9]在研究线性回归问题时,针对异方差样本提出的异方差调整的协方差矩阵相合估计,从而得到相应的异方差调整的t统计量(简称Whitet统计量),Jegadeesh[10]在研究股票月收益的反转效应时采用了该t统计量;最后一种是 Newey 和 West[11]在 White[9]的基础上,针对时间序列样本可能同时存在异方差性和序列自相关性,提出的异方差和自相关调整的协方差矩阵相合估计进而得到相应的t统计量(简称Newey-Westt统计量),如董晨昱等[12]、Wang等[13]、邢红卫和刘维奇[14]均使用了该t统计量。现有文献多是将其中之一直接用于Fama-MacBeth横截面回归和组合水平分析的检验问题中,而鲜有文献提及这四种t统计量的关系及适用性问题,本文旨在追本溯源,试图从四种(尤其是后三种)t统计量的基本原理出发,探寻四者之间的关系,从而明确Fama-MacBeth横截面回归和组合水平分析中的最佳t统计量。尽管组合水平分析作为非参数方法和Fama-MacBeth横截面回归的原理完全不同,但正如上面所提到的,它们为获得最终结果的步骤是完全一样的。因此文中的方法介绍以横截面回归为主,在实证分析中以组合水平分析为主。
1 Fama-MacBeth横截面回归系数的t检验
实证资产定价中被广为使用的Fama-MacBeth横截面回归,是1973年Fama和 MacBeth[1]在研究风险与股票预期收益的关系时首次使用的,也称为两步回归:第一步是在给定时间点上以股票为样本通过最小二乘法进行横截面回归,第二步则是求各系数序列在时间上的均值(作为最终的系数估计值)及相应的t统计量值(用于检验序列的均值是否为0)。具体分析如下:
设yi,τ+1是股票i在τ+1 时点上的收益,x1,x2,…,xk是k个因子,首先在时间点τ(τ=1,2,…,T)进行如下横截面回归:

这里得到k+1个回归系数序列βjτ,τ=1,2,…,T(为了方便,这里不区别参数和估计量的符号)。然后对每个回归系数序列求均值(即Fama-MacBeth估计)和相应的t统计量值。
现有文献中针对Fama-MacBeth横截面回归中系数序列是否有异方差性和自相关性,通常使用普通t统计量、一阶自相关系数调整的t统计量、Whitet统计量和Newey-Westt统计量四者之一。第一种是常用的t统计量,这里不加赘述,第二种是在普通t统计量基础上做的调整,而后两种均来自线性回归的结果。
1.1 普通t统计量和一阶自相关系数调整的t统计量
因子xj是否对未来股票收益有预测作用取决于回归系数βj是否为零,即如下假设:
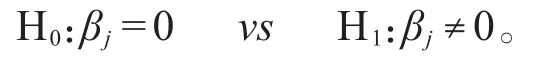
用于检验该假设的样本为βj1,βj2,…,βjT,常使用的t统计量为:
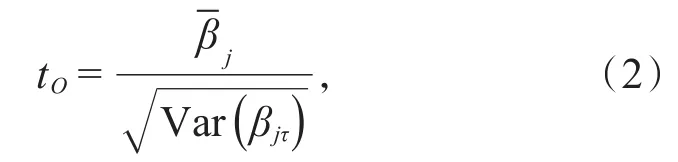
若回归系数序列βj(ττ=1,2,…,T)存在自相关性,且满足AR(1)模型:
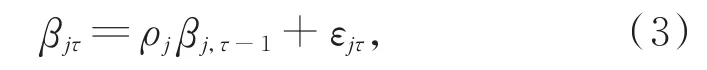
其中,εjτ是均值为 0 的白噪声,ρj为一阶自相关系数,记ρjk为k阶自相关系数,则有。若非零自相关系数的最高阶数充分大,可得如下关系:

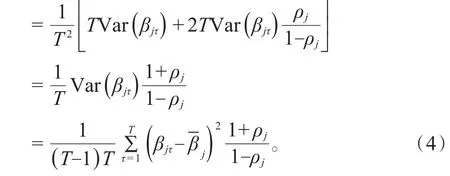
上述近似程度依赖于不为零的自相关系数的最高阶数,非零自相关系数的阶数越高近似程度越好。相应可得在系数序列βjτ满足AR(1)模型时的一阶自相关系数调整的t统计量为:
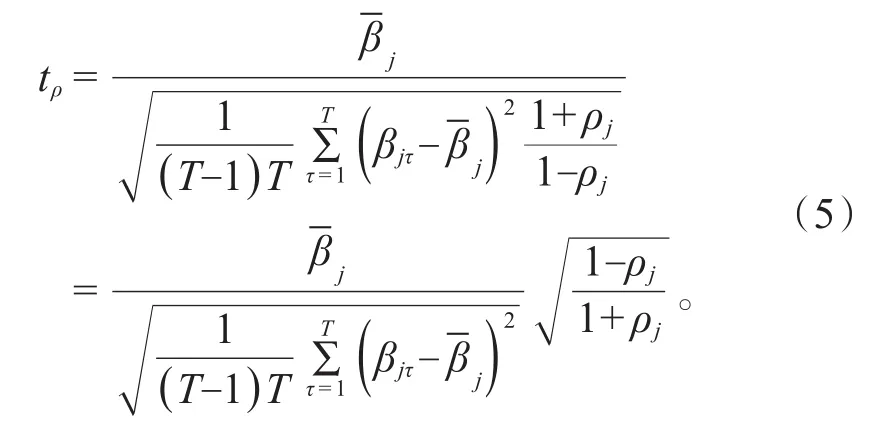
该统计量是在普通t统计量基础上进行的一阶自相关系数调整。Fama等[7],Cooper等[8]均采用了该t统计量。
1.2 Whitet统计量和Newey-Westt统计量
Fama-MacBeth横截面回归和组合分析中的Whitet统计量和Newey-Westt统计量均来自线性回归的结果。这里简单回顾一下多元线性回归系数的White异方差一致协方差矩阵[9]和Newey-West异方差和自相关一致协方差矩阵[11]。设多元线性回归模型的矩阵表示如下:

其中,Y是T维向量,X是T×k维矩阵,β为k维的参数向量,u是T维的残差向量。若u的各分量满足独立同分布,且均值为0,方差为σ2,则回归系数的协方差矩阵为:

考虑到残差序列的异方差性,1980年,White[9]给出了参数估计的异方差一致协方差矩阵:
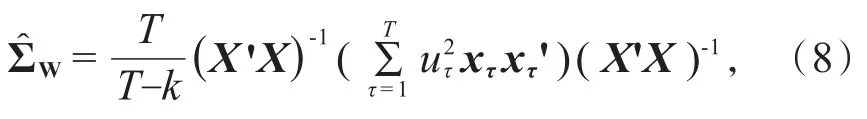
这里xτ是第τ个k维的观测解释变量向量,uτ是第τ个普通最小二乘残差。同时考虑到残差序列可能存在序列自相关性,1987 年,Newey 和 West[9]提出参数估计的异方差和自相关一致协方差矩阵:
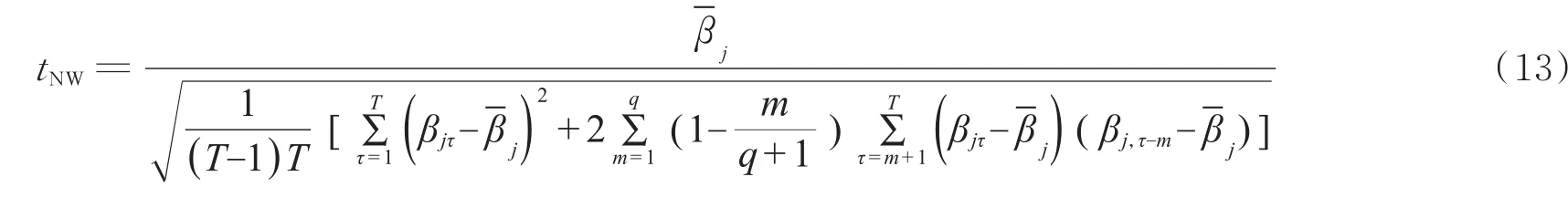
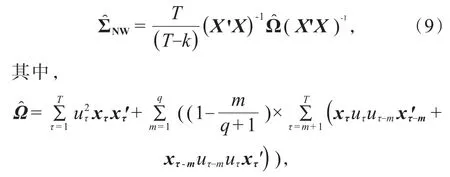
q为残差项的最大自相关阶数,xτ和uτ同上。这里的是两项的和,第一项是为了调整残差的异方差性,第二项是自协方差阵的加权平均,权重随着滞后期m的增加而减小,这一项是为了调整残差的自相关性。
Fama-MacBeth估计相当于对每个回归系数序列建立关于其均值的回归,即:

参数μj的最小二乘估计为对 比上述White的异方差一致协方差矩阵,每个有一个参数μj,回归残差回归只是T维列向量,xτ=1,从而 Fama-Mac-Beth估计的White方差为:
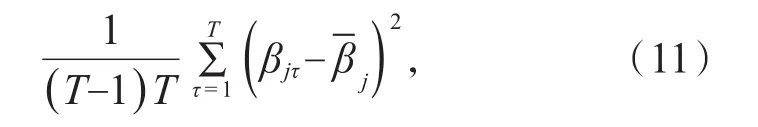
Whitet统计量为:
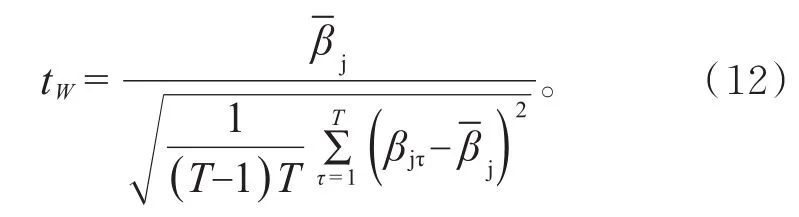
显然,tW与tO一致,这是由于回归模型中只有一个参数,残差项就是样本偏差(样本观测值与样本均值的差),White方差公式中的样本偏差平方和已经反映了序列的异方差性。
同理可获得Fama-MacBeth估计的Newey-Westt统计量见式(13)。q为系数序列的最大自相关阶数。通过上述分析不难看出,文献中常用的四种t统计量事实上只有三种:普通t统计量、一阶自相关系数调整的t统计量和Newey-Westt统计量,且普通t统计量是后两种t统计量在自相关系数为零时的特例。因此,下面主要通过实证分析探讨一阶自相关系数调整的t统计量和Newey-Westt统计量的适用性。
2 实证分析
2.1 数据来源
由于Fama-French三因子模型是实证资产定价研究中最为常用的模型,这里选取美国所有上市公司的规模(Size)和账市比(B/M)十分位组合等权平均和市值加权平均组合收益序列(数据均来自French的个人网站:http://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html)作 为 组合分析的研究对象;股票月末收盘价格、发行量、收益数据来自CRSP(Center for Research in Security Prices)数据库,使用股票价格和发行量数据可获得公司市值(规模)数据;公司的账面价值、盈利和总资产增长率(投资)来自CompustatAnnual and Quarterly Fundamental Files。上市公司的股票月收益、规模、账面市值比、盈利和投资数据作为Fama-Mac-Beth横截面回归的研究对象。样本期为1963年1月至2014年12月,共624个月。
2.2 组合收益序列的自相关性检验
Newey-Westt统计量和一阶自相关系数调整的t统计量都依赖于时间序列的自相关最大阶数,且一阶自相关系数调整的t统计量要求时间序列满足AR(1)模型。这里首先检验了各序列的自相关性,为节省空间表1列出了各序列前八阶自相关系数。
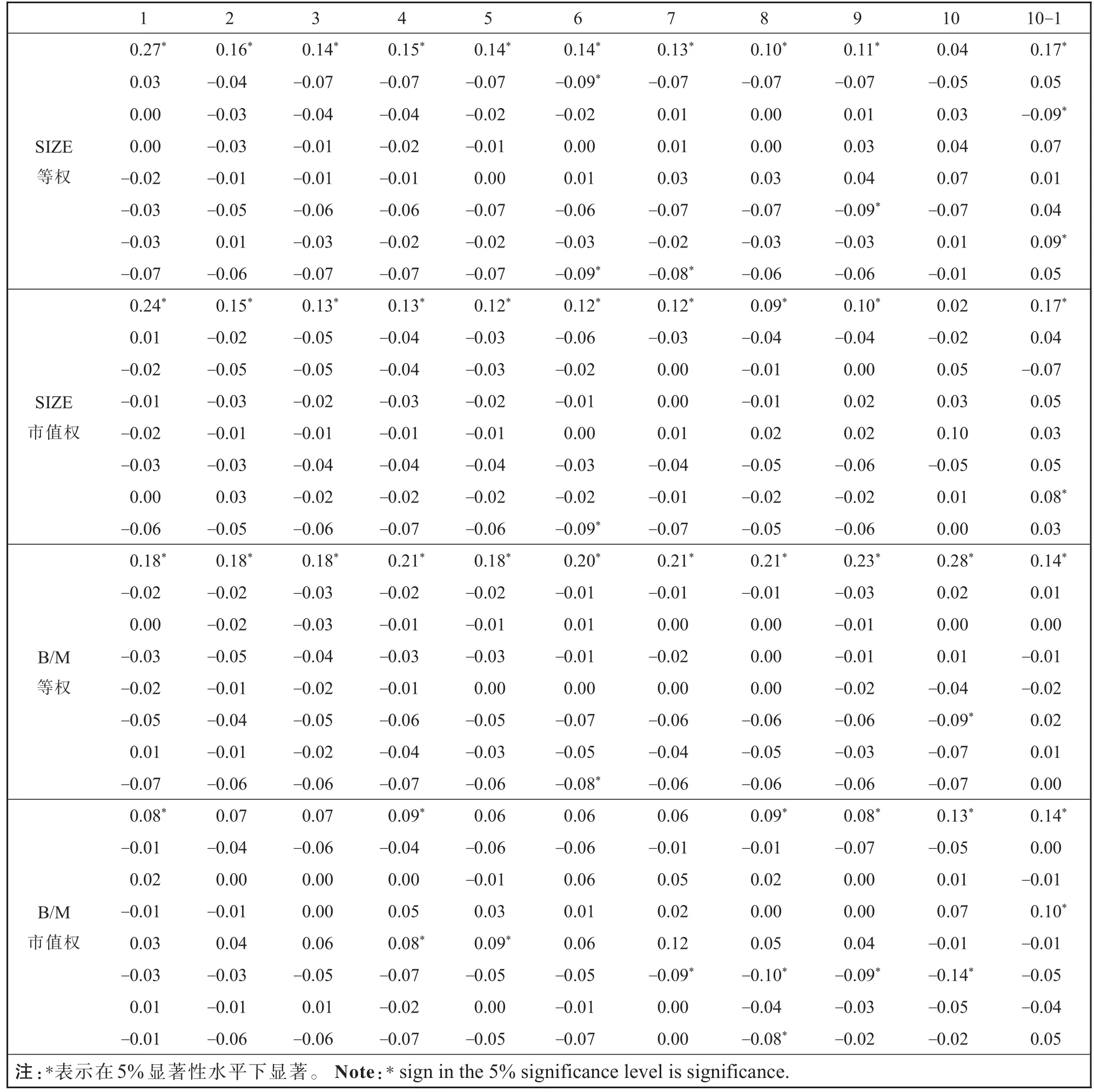
表1 组合收益序列自相关性检验t值Table 1 Portfolio-level profit series autocorrelationttest
从表1可以看出:在5%的显著性水平下,86.36%的序列存在显著正的一阶自相关系数,其中31.82%的序列同时存在显著的高阶自相关系数,因此,对序列进行自相关性调整是必要的。然而,Newey-Westt统计量和一阶自相关系数调整的t统计量哪个更具有一般性?我们可从两个方面加以检验:1)当序列不存在自相关性时,哪一个t统计量的取值更接近普通t统计量值?2)当序列存在显著的自相关性时,其是否满足AR(1)模型?若部分序列不满足该条件,则对所有序列使用一阶自相关系数调整的t统计量是不合适的。
2.3 单变量组合水平分析中的t统计量比较
这里对1963年1月至2014年12月美国所有上市公司的规模和账市比进行单变量组合水平分析,表2给出了各十分位组合收益序列及极端组合收益差序列的均值和各t统计量值(带下划线部分)。每一栏的第一行是序列均值,第二行是普通t统计量,第三行是一阶自相关系数调整的t统计量,最后一行是Newey-Westt统计量(取最大自相关滞后阶数为4①关于Newey-Westt统计量中自相关最大阶数q,曹志广[15]建议q=[T1/3]=[6241/3]=8,([]为四舍五入取整),然而,Newey和West[11]表明异方差和自相关一致协方差矩阵的一致性允许q的增长速度慢于T1/4,因此,这里取q=[T1/4]=[6241/4]=4([]为向下取整)。)。
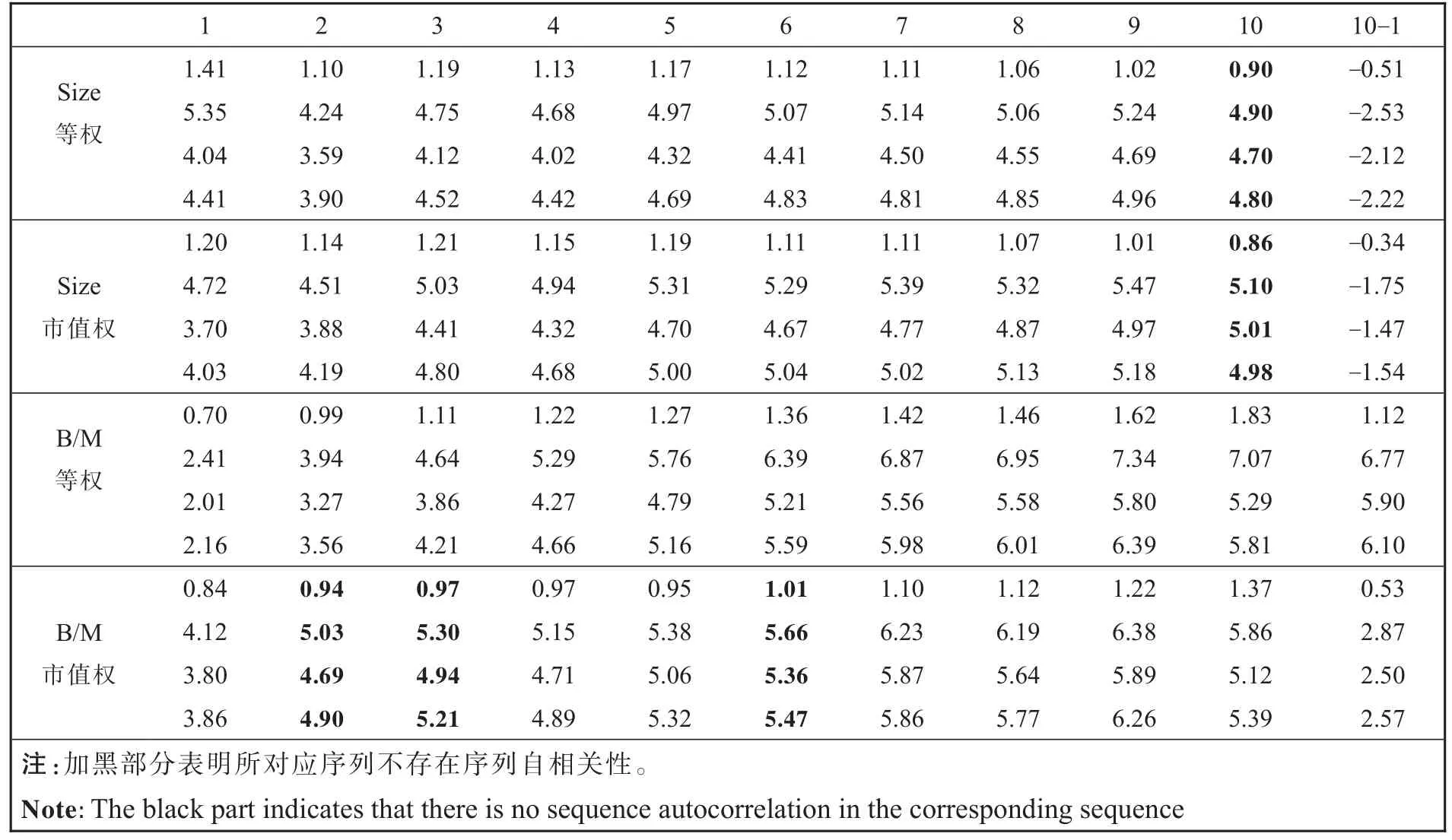
表2 单变量组合水平分析结果Table 2 Results of analysis at the single variable combination level
首先,宏观比较各序列的三个t统计量值,除规模市值加权的第10个组合和账市比市值加权的第7个组合收益序列(Newey-Westt统计量值②在t统计量值的比较中,文中所提到的t统计量值均是指t统计量的绝对值。略小于一阶自相关系数调整的t统计量值)外,其他序列均有普通t统计量值最大,Newey-Westt统计量值次之,一阶自相关系数调整的t统计量值最小。这表明:当序列存在自相关性时,普通t统计量值产生了正的偏差;当序列不存在自相关性时(表2中加黑部分),Newey-Westt统计量值更接近普通t统计量值。
对存在显著自相关的序列,又是否都满足AR(1)模型呢?这里选取规模等权的第六个组合收益序列(该序列存在显著的一阶自相关系数和二阶自相关系数)进行自相关和偏自相关检验。由于该序列的前两阶自相关系数符号相反,不满足的关系,因此可简单判断该序列不满足AR(1)模型。从自相关函数和偏自相关函数图(见图1)也可得同样的结论。对这个序列而言,使用一阶自相关系数调整的t统计量是不恰当的。
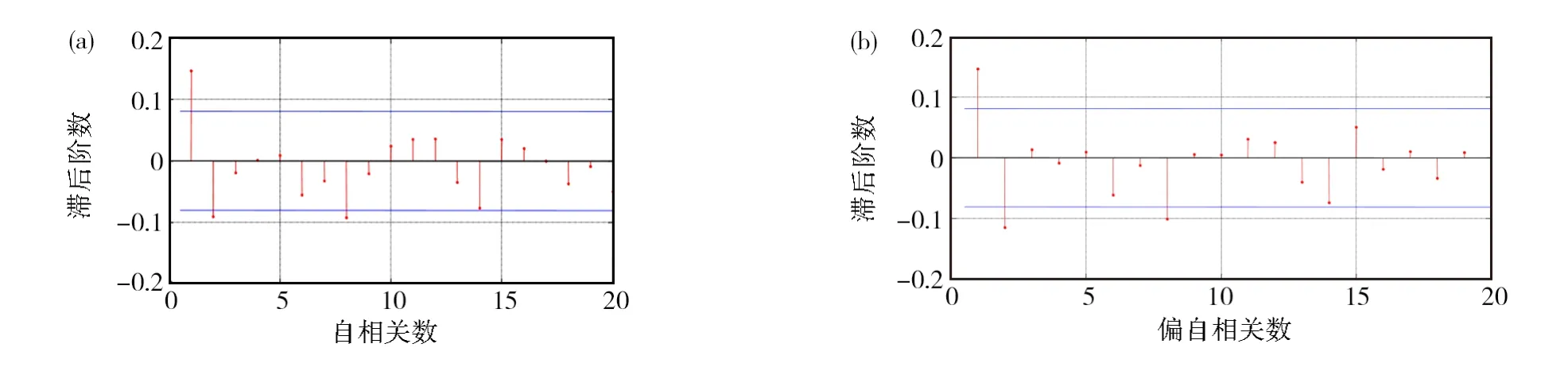
图1 规模等权的第六个组合收益序列的样本自相关(a)和偏自相关函数图(b)Fig.1 Sample autocorrelation(a)and partial autocorrelation function graphs(b)of the sixth portfolio return series with equal weight of scale
存在显著一阶自相关系数的序列中,有68.42%的序列不存在显著的高阶自相关系数,由前面的理论分析部分已知一阶自相关系数调整的t统计量的近似程度依赖于不为零的自相关系数的最高阶数,若序列βjτ(τ=1,2,…,T)仅存在一阶非零的自相关系数时,可得如下关系:

2.4 Fama-MacBeth横截面回归分析中的t统计量比较
这里我们也通过Fama-MacBeth横截面回归对三类t统计量进行比较。建立了股票t+1月的收益(R)关于滞后一期的规模(SIZE)、账面市值比(B/M)、月收益(REV)、盈利(ROE)和投资(INV)的横截面回归:
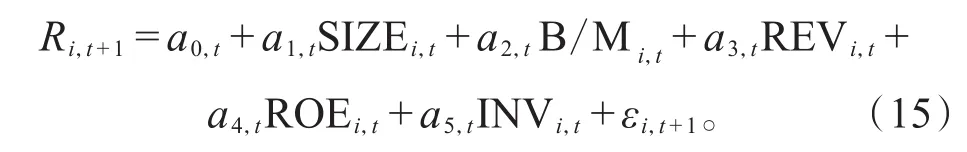
五个回归系数序列均存在显著的二阶以上的高阶自相关性,因此使用自相关系数调整的t统计量是必要的,表3给出了五个解释变量的回归系数及相应的三类t统计量值(带下划线部分)。其中第一行是系数序列均值(回归系数),第二行是普通t统计量,第三行是一阶自相关系数调整的t统计量,最后一行是Newey-Westt统计量(取最大自相关滞后阶数为4)。由于五个系数序列均不满足AR(1)模型,如上一小节的分析,在Fama-MacBeth横截面回归分析中,Newey-Westt统计量更为可信。
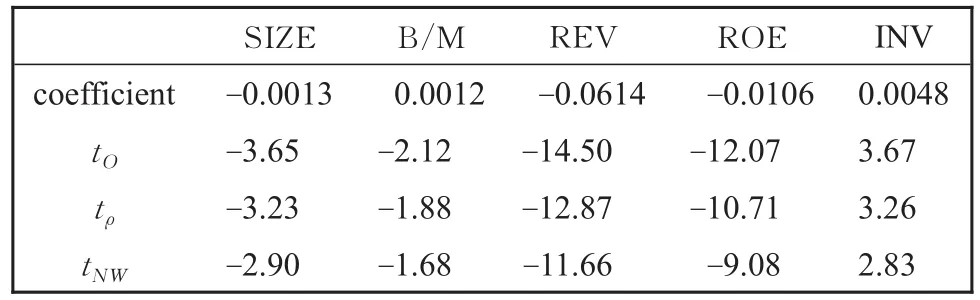
表3 Fama-MacBeth横截面回归分析结果Table 3 Results of analysis on Fama-MacBeth cross section regression
3 结论
关于Fama-MacBeth横截面回归和组合水平分析中的t检验问题,均是关于时间序列均值为零的t检验,由于样本的偏差平方和已经反映了序列的异方差性,因此Whitet统计量与普通t统计量相同,即现有文献中常出现的四种t统计量事实上只有三种:普通t统计量、一阶自相关系数调整的t统计量和Newey-Westt统计量,且普通t统计量是后两者在序列不存在自相关性时的特例。
实证资产定价研究中,如果某一特征变量的极端组合收益差经风险调整后依然显著不为零,表明不能被现有资产定价模型解释的异象的存在,而检验的结果与所选取的t统计量紧密相关。通过对美国股票市场上所有上市公司的规模、账市比十分位组合收益序列和极端组合收益差序列进行自相关分析及对三类t检验统计量进行比较,我们发现,有86.36%的序列在5%显著性水平下存在显著的一阶自相关系数,这些序列的t统计量需要进行自相关系数调整,此时,Newey-Westt统计量相比一阶自相关系数调整的t统计量更准确,且对不存在自相关性的序列,Newey-Westt统计量值更接近普通t统计量值,因此,在三类t统计量中,Newey-Westt统计量用于组合水平分析所得结论更为可信。通过建立股票月收益关于滞后一期的规模、账面市值比、月收益、盈利和投资的横截面回归,得到与组合水平分析一致的结论。

