动力系数反应谱教学中极值法的应用及案例分析
张士科,肖建清,于锦彩
(安阳师范学院 建筑工程学院,河南 安阳 455000)
0 引言
单自由度结构体系在动力荷载作用下集中质点的动力反应,常用动力系数或动力系数反应谱来解析[1]。动力系数也称动力放大系数,是结构动力学中的基本概念,它被定义为质点在动力最大荷载作用下的最大动位移与最大静位移之间的比值[2-3]。动力系数反应谱定义为在动力荷载作用下一系列单质点体系的最大反应(反应谱)与动荷载时间比值(即体系的加载时间和自振周期比值)之间的关系曲线[4-5]。从这两个定义可以看出动力系数与动力系数反应谱既有区别又有联系。另外,在结构力学教材中,它们都是基于单自由度弹性结构体系定义的,因此,内力的动力放大系数与位移的动力放大系数是相同的。
对于单自由度体系在简谐荷载作用下的动力系数及其反应谱,基本上每本教材都有详细的求解过程。但是,很少有教材给出动力系数反应谱的统一求解方法和单自由度在任意动荷载作用下强迫振动的位移和内力动力系数及其反应谱的详细求解过程,特别是线性渐增荷载的动力系数反应谱的求解。在结构力学教学中,很多学生很想了解该部分动力反应谱的求解过程,而不是简单地知道结果。
事实上,在结构力学线性渐增荷载的动力系数反应谱分析时,基于教科书给出的动力荷载位移函数,很难直观地定性分析出动力系数反应谱的形状,并看明白教科书给出的动力系数与时间比值之间的关系曲线。为此,本文提出了任意动力荷载作用下的单自由度结构体系的动力系数反应谱统一的分析法,即极值法。在几种常见的动力荷载下的动力反应中,突加荷载、短时荷载等的动力反应比较简单,而且教科书上都有详细的计算分析过程。因此,文章就以较为复杂的线性渐增荷载为例,推导出动力荷载作用下的单自由度结构体系的动力系数与时间比值之间的函数关系式,通过与教科书的结果比较证明极值法的有效性和正确性。与此同时,该研究内容有助于学生自主参与式地实践学习和认知力学知识的本源,从而激发自己的自主学习能力,实现对力学知识的吸收和掌握。
1 极值法
最值问题是动力结构计算和设计中常常碰到的问题,利用函数的极值求最值是力学中最为常用的方法[6]。现行高等数学教材对极值问题的讲授占用了大量的课时,学生通常掌握的比较扎实,在工程实际中得到了广泛的应用[7]。根据单自由度体系在动力荷载作用下的动力系数及其反应谱定义,不难发现,求解动力系数属于函数在某一区间或区域上的唯一极值点,即最值点;而求解动力系数反应谱属于求解一系列与时间有关的极值问题。因此,提出一种基于极值法的结构动力反应谱的计算方法是有意义的。
在极值算法[8]中,首先,基于实际动力荷载特征建立起力学模型,给出动力荷载与时间的关系式;然后,利用杜哈梅公式求解出动力荷载作用下的动力反应函数关系式;最后,将动力反应函数在与周期有关时间区间上的极值点看作该区间的最值点,从而形成动力反应函数的一系列极值点(动力系数)与时间比值之间的函数关系式,即动力系数反应谱。
2 动力模型描述与构建
2.1 单自由度体系的结构模型
图1所示为有水平支撑的厂房排架结构模型简图,该结构体系集中质量点位于梁与柱的交汇处,质点的质量设为m,有一水平集中力F0作用。在水平梁支撑失效前,假定梁的轴向刚度为无穷大,致使原结构(图(a))处于平衡状态。现假定水平支撑梁失效,为了使原结构仍然处于平衡状态,需要在质点的右侧作用一水平支撑力F,即F0=F,如图(b)所示。

图1 水平振动结构简图
假定水平梁支撑突然失效到再次达到平衡所经历的时间为tr,那么质点右侧作用力随时间变化如图2所示。
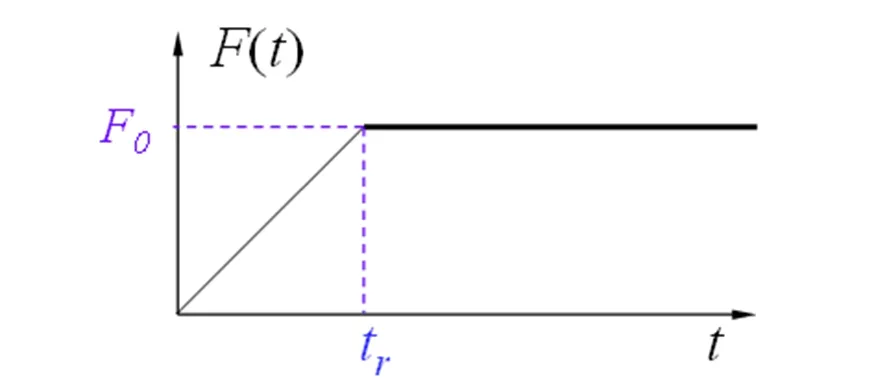
图2 质点荷载与时间关系曲线
当0≤t≤tr时,质点所受荷载F(t)从0线性增长到F0,然后保持荷载不变,最终形成一个线性渐增荷载作用下质点初始位移和初始速度均为0的振动,其函数关系式为:
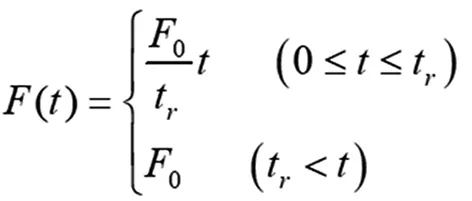
(1)
2.2 单自由度体系强迫振动运动方程
为了分析结构的各种动力反应,首先列出描述动位移的数学表达式,即结构的运动方程[9]。图3所示的模型为水平梁支撑突然失效的水平振动的计算模型。基于达朗贝尔(D′Alembert)原理[10],在线性渐增荷载作用下,单自由度体系的强迫振动方程为:
(2)
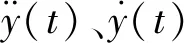
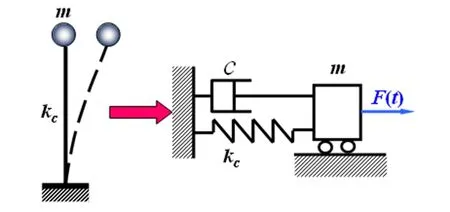
图3 水平振动的计算模型
基于微分冲量导出的杜哈梅积分,即初始位移和速度都为0时,在动力荷载作用下的位移方程,可以得到质点在线性渐增荷载F(t)作用下的动力响应关系式,共分为两个阶段:
第Ⅰ阶段动力位移方程(0≤t≤tr)
(3)
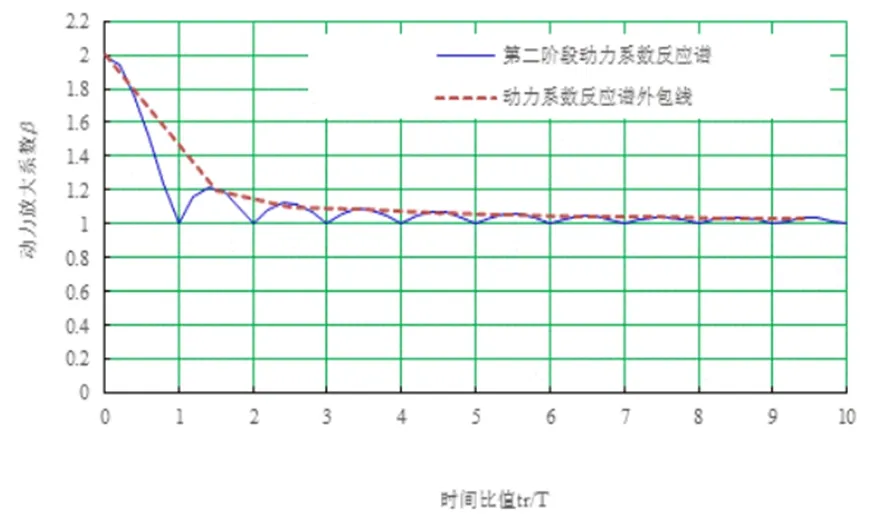
第Ⅱ阶段动力位移方程(tr (4) 已知ω=2π/T,令x=t/T,k=tr/T,可得: (5) 甲烷是矿井瓦斯及天然气等燃料的主要成分,属于易燃易爆气体,对甲烷气体的浓度进行准确实时检测可以避免和预防灾难性事故的发生,保证公共运行和人生安全。传统上对于甲烷气体的检测主要包括催化燃烧技术和半导体气敏技术两种。但催化燃烧技术存在测量范围小,测量元件本身在高温时具有危险性等缺点,而半导体气敏技术同样存在测量围小,以及抗环境干扰能力差等缺点[1]。 最大动位移与最大静位移之间的比值作为动力系数的定义来反映惯性力的影响[11],β=ymax/yst,而动力系数反应谱是动力系数与时间比值之间的关系,其中,最大静位移yst在外荷载一定的情况下是定值。因此,确定动力系数反应谱的核心问题就是如何确定最大动位移。从高等数学中的极值点和最值点关系出发,基于结构工程中的实际情况,可知单自由度结构体系强迫振动的最大动位移可以通过求位移运动方程的极值点获得。所以,要想求最大动位移,只需采用极值法,即将上述两个阶段的位移方程进行求导,得到一系列极值点,进而获得最值点,也就是在该点取得最大动位移。 对第Ⅰ阶段动力位移方程进行求导: (6) (7) (8) 根据动力系数的定义,结合式(7)和(8),可得动力系数表达式为: (9) 对第Ⅱ阶段动力位移方程进行求导: (10) sinπ(2x-k)=0 (11) (12) 因此,可得动力系数表达式为: (13) 根据结构力学教材[2, 12],动力系数反应谱定义为动力系数与动力荷载时间比值k=tr/T之间的关系曲线。因此,对线性渐增荷载而言,渐增荷载时间tr的长短对动力反应有直接的影响,这一结果从导出的公式(9)和(13)也能发现。现采用Excel对第Ⅰ和Ⅱ阶段荷载作用下的动力反应进行分析,图4所示虚线表示线性加载时间在第Ⅰ阶段时的动力系数的反应谱曲线,图4所示实线表示线性加载时间在第Ⅱ阶段时的动力系数的反应谱曲线。结果表明,线性加载时间在第Ⅱ阶段的动力系数的反应谱曲线完全包络了线性加载时间在第Ⅰ阶段时的动力系数的反应谱曲线。根据结构设计原则,即最不利情况,上述两种情况可以统一用第Ⅱ阶段的情况来表达,结果如图5所示,其结构设计工作应以图5所示的外包红色虚线作为设计依据,这些结果与现有结构力学教材[2]上的结果保持一致,但是结构力学教材上只给出了时间比值tr/T<4的结果。 图4 动力系数β与tr/T之间变化曲线 图5 动力系数反应谱及其外包线 从图4和图5可以看出,tr是在整倍数自振周期T内总有一个极值点,动力系数β的变化范围是在1到2之间,随着时间比值tr/T的增大而减小。当tr/T<0.6时,则动力系数β大于1.5,接近于2.0,相当于动力突加荷载情况。当tr/T>10时,则动力系数β小于1.033,接近于1.0,可以认为动力荷载是慢慢作用于结构体系上,几乎不产生动力反应效应,所以可以按静力荷载情况进行计算设计。 由上述结果可以知,极值法非常适用于动力系数反应谱的分析,因为在每一个整时间比值区间或区域内都存在一个极大值,从而形成了一系列的极值。研究结果表明,采用极值法计算得到的动力系数反应谱结果与教材中提供的结果相吻合,这说明该方法是有效的。 另外,研究过程和结果也揭示线性渐增荷载的加载时间t不同,其动力反应谱曲线并不完全一样,教材中提供的动力系数反应谱曲线是一个包络曲线。由于在设计工作中,常以最不利情况作为设计依据,教材中提供的结果也就合情合理。该研究内容有助于学生认知结构动力学知识的本源,从而激发自己的自主学习能力,实现对力学知识的吸收和掌握。
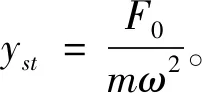
3 动力系数反应谱的推导与计算分析
3.1 动力系数反应谱推导
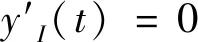
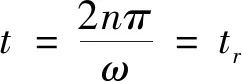

3.2 结果分析

4 结语

