基于双时间尺度的TE 过程控制模型研究

张填昊，赵文志，陈 非，4，王泽青，4，张晓东，4

（1.南京大学 现代工程与应用科学学院，江苏 南京 210023；2.南通职业大学 化工与生物工程学院，江苏 南通 226007；3.东北大学 分子科学与工程中心，辽宁 沈阳 110000；4.江苏汉卿新材料科技研究院，江苏 南京 210000）

0 引 言

在化工行业的研究与生产过程中，Tenessee Eastman（TE）过程被广泛应用于工业控制与优化等领域。因为TE 过程是常见的标准问题，较好地模拟了众多实际工业过程系统的工作环境与设备配置[1⁃3]。一般而言，若模型的复杂程度越高，则TE 过程对实际工业生产的模拟效果越优。因此不断地改进与优化TE 过程的模型，可以更好地模拟与还原化工产品的实际生产过程，从而不断改进化工产品的工艺流程，同时提高化工产业的整体生产效率[4⁃5]。近年来，为了化工生产工艺的改进与优化，大量的国内外学者均对TE 过程的模型与控制性能进行深入的研究，这些研究完成了从无机理模型到复杂机理模型的进展，具有较为重要的意义[6]。然而这些研究仍应用单时间尺度的概念，还未实现TE 过程模型的进一步改进和深度优化[7]。因此，如何建立TE过程的细化分层与先进控制模型，是目前化工生产系统亟需解决的重要问题。

针对这一问题，本文在具有大量参数的多变量系统中，通过引入双时间尺度的概念，对包含气液两相的TE过程进行双尺度建模，从而较好地模拟了实际化工系统的多种参数随时间产生急剧变化的动态过程。同时利用微分方程的计算方法获取更加精确的系统动态响应，得到了温度与压力的模型方程，并提出了TE 过程的拟稳态和全动态控制模型。该模型的GPROMS 仿真实验数据表明，在控制效果方面，基于双时间尺度的控制模型与基于单时间尺度的控制模型具有基本相似的控制效果，但在能量控制方面，基于双时间尺度的控制模型具有更优的控制效果。

1 TE 过程

1993 年，在缺乏过程控制技术的研究与评估技术的背景下，Downs 与Vogel 根据Eastman 公司的实际化工生产过程，提出了具有工业级的TE 过程控制方法。随后，该方法被广泛应用于统计过程监控、传感器故障检测和故障诊断、监控等领域，为化工行业的工艺改进和效率提升做出了重大的贡献[8⁃9]。

一般而言，TE 过程可分为8 个组，即A～H。在这些组分中，A、C、D 与E 表示4 种化工系统的反应物，而G与H 表示系统在化工反应之后得到的两种产品，B 表示生产过程中原料的惰性气体，F 是反应过程产生的副产品。其具体的反应过程如下：

这些反应均属于不可逆的放热反应，其反应速率遵循Arrhcnius 方程。此外，TE 过程的工艺流程主要由反应器、分离器、混合区域与汽提塔等部分组成，其主要原理为气相反应物和催化剂被添加到反应器中，通过化学反应产生液相产品。其中，由于存在冷却设备，所以反应器可以带走多余的热量。同时，因为无液相出口，产品与剩余原料均以气相的形式离开反应器，而催化剂是难以挥发与不溶于液体的固体，仍存在于反应器中。利用该原理，TE 过程可以正常地发生受控制的化学反应，并生成产品G 与H，而惰性气体B 与副产品F 利用分离器即可被排出。TE 过程的组分物性数据如表1 所示。

2 建模原理

在TE 过程中，本文需要对消耗的物料与能量进行衡算，从而建立TE 过程的模型方程。考虑化学反应的物料生成与消耗，物料与能量的通用衡算关系式为：

式中：RI与RO分别表示反应物料的输入速率与输出速率；RC表示累计速率，即反应参数对时间的导数。在物料衡算时，S表示化学反应的反应速率；在能量衡算时，S表示化学反应的反应热。

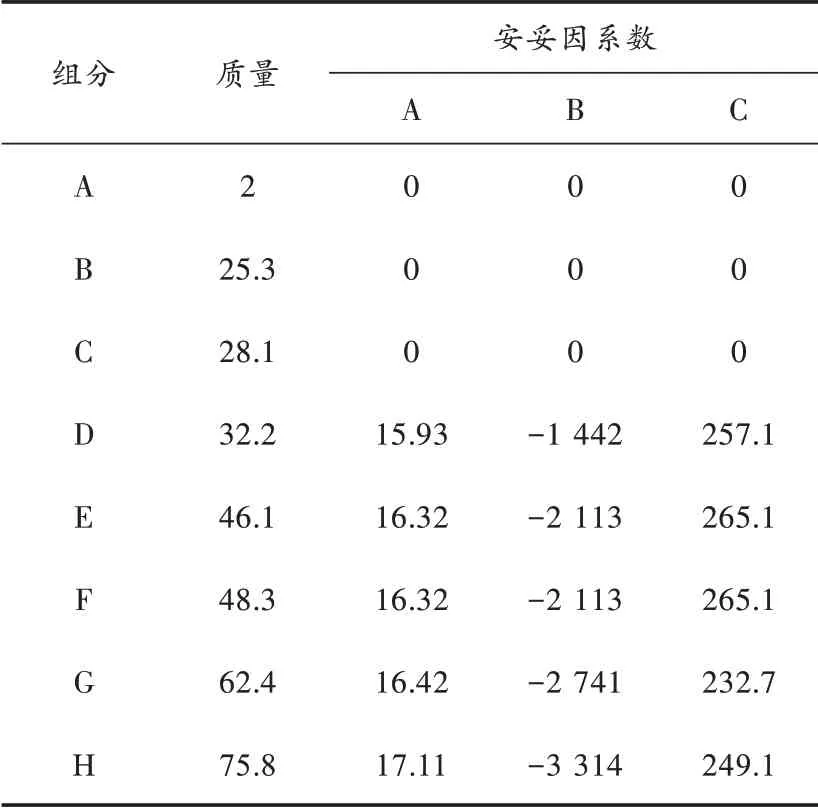
表1 TE 过程组分物性数据

在化工生产过程中，TE 过程由反应器、分离器、汽提塔与混合区域组成。在这些组成部分里，反应器、分离器与汽提塔均为气液两相，而混合区域是全气相。其中，若气相与液相同时存在于化学反应中，则气相主导的压力与液相主导的温度具有不同的动态特性，两者存在一定的关联性，但其动态方程却并不相同[10⁃13]。通常利用气相物料与气相能量平衡方程，可以推导气相温度与压力的动态方程。使用液相物料和液相能量平衡方程，可以推导液相温度与压力的动态方程。利用上述双时间尺度建模思想，引入机理建模方法等基本原理。在物料与能量衡算、多种化学反应动力学方程的基础上，本文可以得到反应系统性能的代数方程组或微分方程组。

3 动态建模

为了得到TE 过程的动态模型，基于调节阀等反应信息，本文深入探讨了反应器、分离器与汽提塔的容积设计，从而实现反应控制。

3.1 容器尺寸设计

文中对反应器、分离器与汽提塔的容器尺寸进行了细致的设计，其具体内容如下。

1）通过查阅相关文献，本文将气相容积设置为Vg=20.25 m3，反应器（圆柱型）的液相容积设置为Vl=16.55 m3，设圆柱的底面直径dg是其高度hg的，则利用圆柱体的体积公式计算如下：

可以计算出底面直径dg=2.86 m，高度hg=5.72 m，而液位高度为2.57 m。

2）本文将分离器的液相容积设置为Vl=4.88 m3，若气相容积是液相容积的1.5 倍，则利用式（3）计算得到分离器的气相容积Vg=7.32 m3，底面直径dg=1.98 m 且垂直高度hg=3.96 m，液位高度为1.58 m。

3）文中设置汽提塔的液相容积Vl=4.43 m3，Vg=6.65 m3，dg=1.92 m，hg=3.84 m，其液位高度为1.53 m。

3.2 全动态模型

在气相与液相平衡分析的基础上，利用双时间尺度建模原理假设所有的反应气体均处于理想的状态，所有的物料被均匀混合，气液分离均可达到平衡状态，同时忽略气相管路。本文提出了TE 过程的全动态模型，其详细内容如下。

在TE 过程中，反应器的物料通常来源于混合区域。当所有的气相、物料与催化剂被添加到反应器后，TE 过程的化学反应快速发生，而处于气体状态的产品被送去分离器。令与Ei分别表示各个组分的反应速率和反应活化能，χi表示反应的相关系数，R表示气体常数，T表示反应器的气液相温度，Vvr表示反应器的气相体积，Pi,r表示各组分的气相分压，则反应器的反应速率方程如下：

利用热量、气相、液相与冷却水等平衡方程，本文得到气相流股方程式如下：

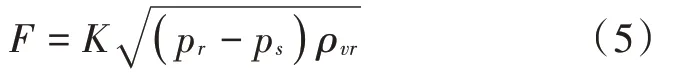
式中：F表示气相的物料流量；K表示流量系数；pr与ps分别表示反应器内外的气相压力；ρvr表示气液相的平均摩尔密度。需要说明的是，文中推导了大量的方程，包括物料、热量与进料等平衡方程。但限于篇幅的原因，文中仅展示全动态模型的核心方程。

3.3 拟稳态模型

在TE 过程的全动态模型中，对温度与压力进行一定的简单处理后，即可得到TE 过程的拟稳态模型，其具体内容如下。

1）温度

利用双时间尺度原理，将气相与液相中的温度分别求解，可以获取两者的变化特征。其中，气相温度变化的速率较快，而液相温度变化的速率较慢，最终这两者趋向于相同。在拟稳态模型中，本文统一气相与液相的温度，令T表示统一之后的温度参数，t表示反应时间，FI，FV与FL分别表示反应进口、气相出口和液相出口的流量，hI，hV与hL分别表示反应进口、气相出口和液相出口的焓值，AU表示反应过程中冷却装置的换热量，σ，cp与VL分别表示液相的密度、比热和体积。则温度的模型方程为：

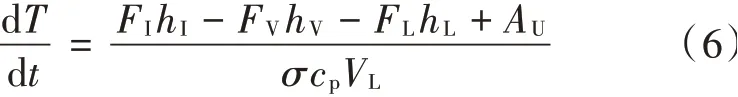
2）压力

由全动态的模型方程可知，压力参数与气相物料、温度、液相物料等参数密切相关。综合这些因素，利用理想气体的状态方程，本文分别推导了不可凝组分与可凝组分的分压方程，如下：

式中：I=A,B,…,H，即各种组分；P1I与P2I分别表示不可凝组分和可凝组分的分压计算结果；R是理想气体的状态常数；V表示气相的体积；P0I表示组分I的饱和蒸汽压。

4 仿真结果与分析

为了验证控制模型的有效性，文中利用GPROMS流程模拟软件，对传统的单时间尺度模型与本文的控制模型进行仿真和对比。其仿真结果如表2、表3 所示。

表2 两种控制模型的反应器气相含量

表3 两种控制模型的反应器状态变量

由表2 可知，在GPROMS 仿真中，若提供同样的反应条件与物料消耗，则双尺度模型的多种气相含量高于单尺度模型。由表3 结果可知，在同样的外部条件下，双时间尺度模型中反应器状态变量的统计精度要高于单尺度模型。综合表2 与表3 的结果可知，与经典的单时间尺度模型相比，基于双时间尺度的控制模型具有一定的优越性与更优的有效性。换言之，基于双时间尺度的TE 过程控制模型具有一定的借鉴意义与参考价值。

5 结 论

基于双时间尺度的建模原理，本文提出TE 过程的全动态与拟稳态模型。全动态模型分别提供了详细的压力与温度动态方程，对化学反应的各个阶段进行细致的刻画，拟稳态模型给出了压力和温度等总体参数的计算方程。此外，利用GPROMS 软件，文中验证了TE 过程拟稳态模型的有效性与优越性。然而，在仿真条件和计算资源的限制下，本文还未能对该模型的稳定性进行测试与仿真，将在未来的研究中解决这一问题。