基于ACE法和模拟退火算法的土层等效参数反演*

曹净 李豪

(昆明理工大学建筑工程学院 昆明 650500)

0 引言

位移量是一种描述物体在受力情况下变形形态的重要物理量，当前已被用来作为反分析确定岩土参数的主要依据，利用现场实测信息的反演方法成为获取岩土体物理力学参数的一种新的可行途径，并表现出了独特的优势[1-3]。在实际工程中，因为基坑或边坡的支护结构位移是较为容易测得的，利用工程现场所测得的支护结构实际位移值对岩土物理力学参数进行反演分析的方法在实际工程应用中较为普遍。

利用实测数据进行岩土参数的反演，其目的就是将岩土参数的反演问题变为相应目标函数的计算寻优问题，但是由于岩土自身特性的复杂性，构造出的目标函数多为含有多峰的复杂非线性函数。对于传统中利用多个约束条件对其目标函数进行计算得出参数值的方法，所得结果在一定程度上依赖于对约束条件和初始值的选取，且容易使目标函数陷入局部极值。许多学者也提出利用BP神经网络和遗传算法等智能算法对土层参数进行反演，但是其计算量大，计算时间长且收敛速度较慢[4-5]。因此，本文提出结合均匀试验和ACE法的方法来建立出一种土层参数与支护结构位移之间的函数关系，构建出高效响应面，在此基础上，运用插值运算得出土层参数的响应值(支护结构计算位移值)，最后结合模拟退火法对根据响应值和实测位移值构造出的反演目标函数进行解(土层参数)的寻优，来获得更为合理的土层等效物理力学参数。

1 构建响应面的基本理论

1.1 均匀试验

均匀设计试验法[6-7]最开始由方开泰和王元两位学者在1978年提出，此种方法是基于试验点均匀散布在整个试验范围内的，且从均匀性的角度出发来提出的一种试验设计方法。均匀试验方法相对于优选法和正交试验法，其试验次数更少，效果更好。均匀试验的设计过程如下列步骤所示：

(1)依据所研究的对象，确定出设计因素(变量)的个数，在因素个数确定的情况下选择具有合适水平数(m个水平)的均匀试验表。

(2)确定出各个因素的取值区间[Ximin,Ximax](i=1,2,…,n)，其中Ximin、Ximax分别为第i个因素的最小值和最大值，n为因素的个数。

(3)根据均匀试验表选择出的水平数安排m次试验，并将每个因素划分为m等分的情况：

(1)

式中，i=1,2,…,n，为因素序号；j=1,2,…,n，为每个因素水平序号；Xij则为第i个因素的第j个水平值。

(4)采用均匀试验表组配试验来实现均匀试验设计。

1.2 ACE非参数回归技术

非参数回归技术，其实质就是在输入与输出数据确定的基础上，来找出两者之间的映射关系，也即响应面函数。采用ACE[8](Alternating Conditional Expectations)非参数回归技术，不需要一开始设定出响应面函数的形式，而是寻找出输入数据组X1，X2，…，Xm的映射值φ1(X1)，φ2(X2)，…，φm(Xm)和输出数据y的映射值θ(y)，使其满足：

θ(y)=φ1(X1)+φ2(X2)+…+φm(Xm)+ε

(2)

确定响应面函数：

y=θ-1[φ1(X1)+φ2(X2)+…+φm(Xm)]+ε

(3)

式中θ-1[.]为θ[.]的逆函数，ε为拟合误差。

如果确定了φ1(X1)，φ2(X2)，…，φm(Xm)和θ(y)，那么也就可以确定出响应面函数关系，可以直接调用统计学软件S-plus中提供的ACE数据包来获得上述映射值。

1.3 插值计算

通过ACE回归技术分析得到相应数据的映射值之后，从而进行拟合映射值来求解θ-1[.]，建立出响应面关系来得出如式(3)的显示响应面函数。如果在变量较多时的试验数组，其拟合函数关系非常复杂，而且进一步的拟合会产生出新的误差。因此，通过采用简单的插值法来直接进行输入参数组的输出值计算，来避免上述复杂拟合计算过程[9]。

由均匀试验得到的输入因素X1，X2，…，Xm中，各个因素的区间内均由n个计算点组成，并且计算点是均匀分布的，那么就能生成较密集的插值点。对于在各个计算区间内的任意输入参数xi，即可根据响应面关系直接进行插值运算来得出相应的输出参数yi。

φi(Xi)=interp(Xi，φi(Xi)，xi)i=1,2,…,m

(4)

则

(5)

则输出yi为

yi=interp(θ(Y)，Y，θ(yi))

(6)

式中，Xi=[Xi1,Xi2，…，XiN]是由均匀设计确定的变量xi的各个水平组成的试验向量，φi(Xi)是与该试验向量对应的变换值且φi(Xi)=[φi(xi1，xi2，…，xiN)]，Y是试验输出结果向量，θ(Y)是Y的映射值。通过MATLAB编写相关程序语言实现从式(4)到式(6)的过程，即可完成Xi与Y之间的插值计算。

2 模拟退火算法基本原理

模拟退火算法[10](Simulated Annealing，SA)，它是一种基于Monte-Carlo迭代求解策略的随机寻优算法，其优点在于对目标函数进行求解时可以避免陷入局部解。算法思想来源于工业中对固体进行退火的原理，在对金属固体进行热加工时，退火就是先将固体加热到某一种高温状态下，而后徐徐进行降温的过程。在加温时，固体内部中的粒子随着温度的升高而成为一种无序状态，并且内能增大。在徐徐降温的过程中粒子渐进有序地在每个温度下达到平衡状态，最后在某一低温下达到平衡。模拟退火算法就是在固体退火的机理上建立起的一种寻优算法，其能够在一定概率下搜索出目标函数的最优点。

2.1 模拟退火算法的模型要素

(1)解空间。该空间由在指定前提或者约束条件下的诸多可行解构成。

(2)目标函数。目标函数一般为由已知条件给定的，需要进行优化计算的函数，其最大(小)点所对应的参数为所需的最优解。

(3)可行解状态改变规则。在一定的概率情况下，由一个可行解(xold)向另一个可行解(xnew)进行转换，判断其xnew是否能被接受，最常用的接受准则是Metropolis准则。

(4)温度Tk下降规律。指由一高温状态向一低温状态冷却的降温规则。为了计算简洁明了，在实际应用中，常用式(7)来表示降温规律：

Tk=αTk-1

(7)

式中，α为小于1 的数，根据不同实际情况，其取值区间常为0.5～0.99。

2.2 模拟退火法的思想步骤

(1)初始化：设定出初始解的状态xold(算法迭代的起点)，初始温度T、终止温度Tk以及每个温度下的迭代次数L。

(2)在迭代L次数下，产生新的可行解(xnew)，并计算增量△=C(xnew)-C(xold)，其中C(xold)为评价函数。

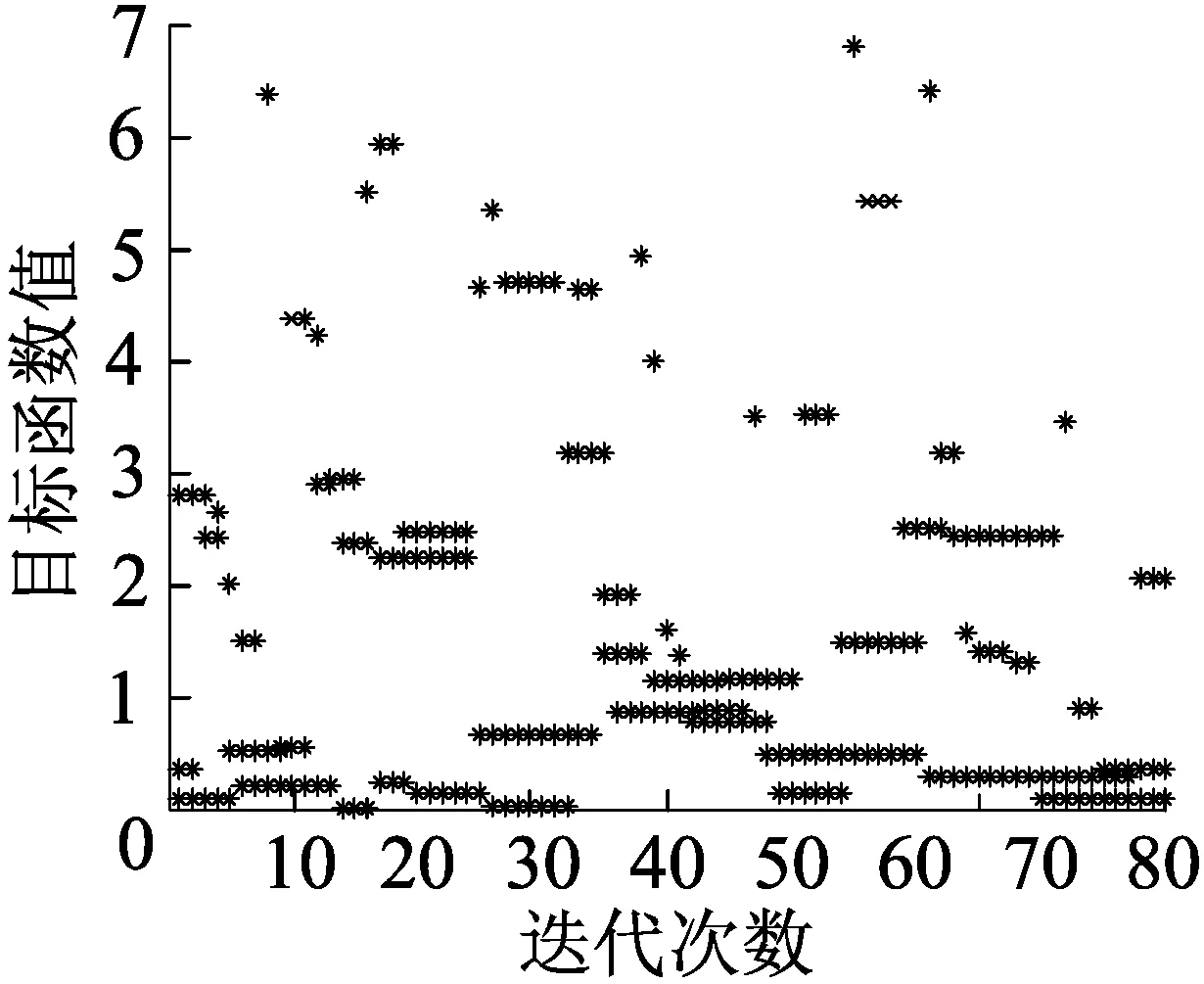
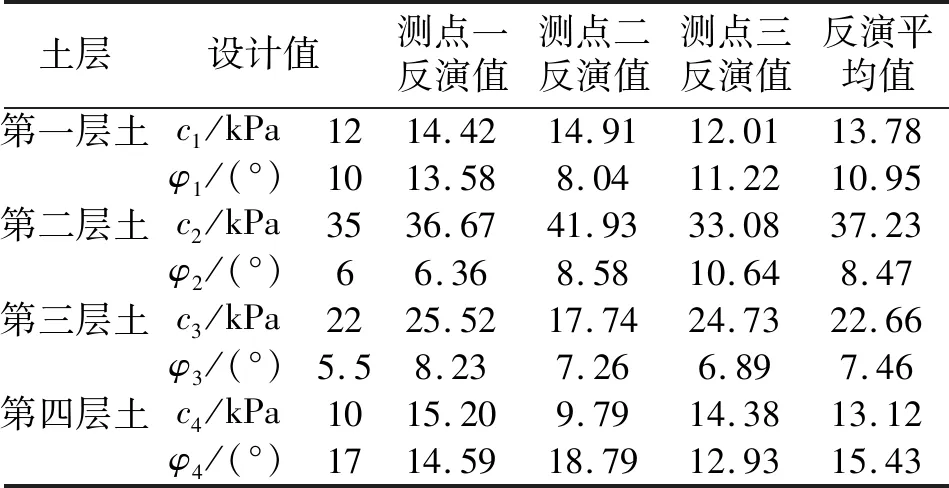
(3)利用Metropolis准则进行当前解的判断：若△<0则接受xnew为当前解，否则生成一个[0,1]区间上均匀分布的随机数λ，若λ

(4)满足终止条件后，输出当前解为最优解，并结束在某一温度下的程序计算。

(5)T根据降温规律逐步减少，若T>Tk则返回第二步，直到达到终止温度，程序计算结束。

3 基于ACE法和模拟退火算法的土层等效参数反演

进行土层参数反演的实质就是寻出一组待反演的参数，并且使与之相应的支护结构位移计算值与位移实测值不断地逼近。其最终目标函数可取为

F(xi)=|f(xi)-μ|

(8)

式中，xi为某一组的反演参数，f(xi)为反演计算位移值，μ为相应位置点的实测位移值。

进行土层参数反演的计算步骤为

(1)按照计算案例，合理确定出岩土参数的取值范围，并根据均匀试验构造出计算方案。

(2)根据均匀试验表所构造出的样本组，按照规范算出每个样本组下的计算位移值。

(3)将均匀试验构造出的样本组作为输入数据，对应样本组计算出的位移值作为输出数据，利用ACE法进行两者之间的映射，构建出响应面。

(4)运用响应面关系进行插值得出响应值，并结合实测数值构造出目标函数，然后根据其函数增量的范围选择退火策略，设定出合理的初始温度，并给出每个温度下的迭代次数，相比于进行大范围的盲目计算，此方法有利于提高效率。

(5)给出退火算法的初始状态(即土层参数的初始值)，将其作为当前的最优点，并代入响应面进行插值运算，得出计算位移值和目标函数值。

(6)对当前最优点在响应面计算区间内进行随机变动，产生出新的最优点，代入响应面进行插值运算，得到计算位移值，最后计算得出新的目标函数值以及目标函数增量△。

(7)对增量△进行判断，若△<0，就接受新产生的最优点为当前计算中的最优点；若△≥0，则生成一个[0,1]间均匀分布的随机数λ，若λ

(8)如果没有到达某一温度下的迭代次数，就回到步骤4继续迭代计算。

(9)如未达到冷却终止温度，则转回步骤6；如达到终止温度，就输出当前计算中的最优点，结束计算。

4 应用算例

算例为昆明市五华区某基坑工程，本文选取此基坑工程7-7剖面进行反演分析。基坑7-7剖面采用桩锚支护系统，其开挖放坡坡高为3.0 m，取台面为1.0 m，坡比1∶0.83。支护桩为旋挖桩，桩径0.8 m，桩长32 m，间距1.1 m。基坑从上至下一共设置了1排土钉和3排预应力锚索，具体的支护情况见图1。7-7剖面中坑底以上范围共有4层土，各土层相应的物理力学指标见表1。

表1 土层物理力学指标

图1 基坑支护简图(单位：mm)

基坑7-7剖面施工工况如下：①工况一：基坑开挖至3.8 m(含0.5 m超挖深度)；②工况二：在3.3 m深度处施加第1排锚索；③工况三：基坑开挖至5.8 m(含0.5 m超挖深度)；④工况四：在5.3 m深度处施加第2排锚索；⑤工况五：基坑开挖至8.3 m(含0.5 m超挖深度)；⑥工况六：在7.8 m深度处施加第3排锚索；⑦工况七：基坑开挖至9.7 m(到达坑底)。当基坑开挖至基坑底后，基坑开挖工程基本完成，所测得的支护桩位移数据基本开始稳定，故分别选取工况七中地面以下4 m深度处(测点一)、5 m深度处(测点二)和8 m深度处(测点三)的支护桩实测位移值来作为目标函数(式8)中的实测数据。

在构建响应面之前，将每层土的物理力学指标作为随机参数，为了使响应面涵盖的范围足够大，考虑实际工程中可以接受的参数范围，将参数的范围尽可能地扩大，见表2。根据文献[5]中均匀试验表的建立过程，构建出一个8因素、30水平的均匀表，均匀表构建采用方幂法，利用MATLAB编程得到均匀表U30(308)，将各个参数的取值范围分为30个水平，代入建立的均匀表，即得出输入样本。根据《建筑基坑支护技术规程》(JGJ 120—2012)[11]的相关规定，依次计算出不同试验组下测点一、测点二和测点三的支护桩位移来作为输出数据组。输入和输出数据见表3。

表2 土层物理力学指标取值范围

表3 均匀试验输入及输出数据组

获得输入和输出数据之后，即可通过ACE非参数回归的方法构造出两者之间的高效响应面，此步骤直接调用统计学软件S-plus中的ACE回归的数据包，分别对测点一、测点二和测点三对应的30组试验逐一进行回归，其回归拟合系数均高达0.99，限于篇幅，只给出测点一的输入与输出数据的映射值，见表4。然后在所给的每个参数范围内进行参数的随机选取，根据已经确定的响应面进行插值运算，计算出每组参数对应的支护桩计算位移值，并代入目标函数(式8)中，最后利用模拟退火算法以目标函数最小值为目标来进行解(土层参数)的计算选取。

表4 测点一的输入及输出数据映射值

根据前文第2.2节中对模拟退火算法接受坏解概率的Metropolis准则的描述：若△<0则接受xnew为当前的解，否则生成一个[0,1]间均匀分布的随机数λ，若λ

图2 不考虑初始温度的目标函数值随迭代次数变化

图3 测点一的目标函数值随迭代次数变化

图4 测点二的目标函数值随迭代次数变化

图5 测点三的目标函数值随迭代次数变化

对表5中的反演结果与设计值进行对比分析，发现基于ACE法和模拟退火算法反演得出的每个测点下的土层参数值与设计值稍有偏差，可能的原因是基坑开挖过程是一个卸载的过程，开挖的过程中的土层卸载会使土体实际抵抗变形的能力降低，对计算造成一定误差。由于单个样本组的反演结果可能具有一定的偶然性，应结合实际对比分析多个样本组的结果，由表5可以看出，3组反演计算结果的平均值与设计值较为接近，说明利用该方法进行土层等效参数的反演具有一定的可行性。

表5 土层等效参数反演计算结果

5 结论

(1)响应面法通常用来处理较复杂系统的输入与输出之间的映射关系问题，其计算量小并且适用于复杂的非线性问题。本文将均匀试验和ACE法融合在一起，利用ACE法的非线性映射能力，构建出参数之间高效响应面，极大地简化了计算过程，提高了反演的计算速度，再结合模拟退火算法对利用响应值与实测值构造的目标函数进行参数解的寻优，以一定的概率搜寻出最优参数解。将这一算法模型对一工程实例进行运用，发现其在解决变量与目标函数之间无明显的数学表达式的工程问题时具有一定的可行性。

(2)模拟退火算法的运用，极大地依赖对初始参数的选取，针对不同的计算案例，应考虑需要求解数据的实际情况，分析目标函数增量与退火温度的比值对收敛性的影响，经过调试选取出合理的初始

参数，再结合算例进行不同数据组的计算，这样有利于提高计算的效率。在计算的过程中可以发现，由于模拟退火算法有接受坏解的概率准则，容易丢失计算过程中更好的解，如何将计算过程中所有解保存下来重新挖掘有效数据，进而提高计算的精度是下一步需要深入研究的内容。