堆积体内部裂隙对降雨入渗的影响

邱 潇，涂国祥，赵石力，侯孝东

(成都理工大学 地质灾害防治与地质环境保护国家重点实验室，成都 610059)

1 研究背景

由堆积体构成的边坡在我国广泛分布，该类坡体具有结构松散、渗透性大、可变性强等特点[1-2]。强降雨作用下，边坡易发生失稳破坏，将会给人民生命财产带来巨大损失。研究[3-4]表明，降雨入渗会使土体内部孔隙水压力升高，饱和度增加，抗剪强度降低。因而研究雨水在堆积体内部渗流规律对评估降雨条件下边坡稳定性至关重要。目前众多学者对此展开了深入的研究。左自波等[5]对不同级配堆积体进行室内降雨试验，发现湿润锋到达后，土体体积含水率及孔隙水压力逐渐增加，而基质吸力持续降低。李焕强等[6]利用人工模拟降雨试验，对不同坡角边坡进行研究，得出含水率及边坡变形的变化规律。董辉等[7]通过对堆积碎石土入渗规律研究，发现湿润锋迁移速率随雨强增加趋于线性增长。徐光明等[8]、Huang等[9]、王一兆等[10]通过改变土体密实度、水位、降雨与停雨时长来探索边坡含水率、孔隙水压力的变化规律。

表1 部分裂隙发育情况Table 1 Development of fissures

上述研究考虑了多种因素对降雨入渗的影响，然而在自然界中，由于自然风化及滑坡蠕动等因素作用，坡体表面会产生不同发育程度的裂隙。降雨过程中，雨水通过裂隙很快到达土体内部，其入渗规律会发生显著的改变。一些学者对此做了一定研究，如姚海林等[11]、郑少河等[12]对裂隙性膨胀土降雨入渗规律进行了研究。刘登生等[13]通过Geo-studio软件进行研究，认为坡体表面发育的裂隙长短及角度对降雨入渗过程有较大影响。但是自然界中裂隙的发育形态各异，且人们对裂隙对边坡入渗的影响还未形成统一认识，尤其是在降雨过程中还需考虑长短裂隙之间的相互影响。

自然界中，深厚型堆积体发育各种类型的裂缝是一种常见的现象，这些裂缝可以为降雨入渗提供良好的入渗通道。这可能是降雨入渗诱发深厚型堆积体失稳破坏、形成深层滑坡的重要原因。但对于降雨在裂隙型深厚堆积体中的入渗-运移机理以及触发堆积体失稳破坏的机理仍需要深入探索。

澜沧江上游河谷的右岸发育一高位巨型古滑坡。目前该滑坡处于蠕动变形阶段，滑坡体上发育大量张开型裂缝，这些裂缝延伸长度一般在数米至百余米不等，张开宽度一般约2～50 cm，个别宽度可达数米。这些裂缝的存在，为后续降雨提供了良好的通道，从而加速该滑坡的复活过程。基于此，本文采用物理模拟和数值模拟的手段，探索降雨在裂隙型堆积体中的入渗-运移机理，以期为后续的滑坡复活机理研究和稳定性评价提供参考。

2 滑坡体裂隙发育特征

研究的堆积体为澜沧江某巨型古滑坡，分布高程2 620～3 060 m，据勘探资料，滑坡体体积约400万m3，覆盖层厚度约25～70 m，平均厚度35 m左右，以角砾质碎石土为主，成分主要为砂岩、板岩，全-强风化状态，结构松散。堆积体地表分布大量形状各异、大小不一的拉张裂隙和剪切裂隙，整体上裂隙形态以主-次平行裂隙为主，滑坡体范围及部分裂隙情况详见表1和图1。

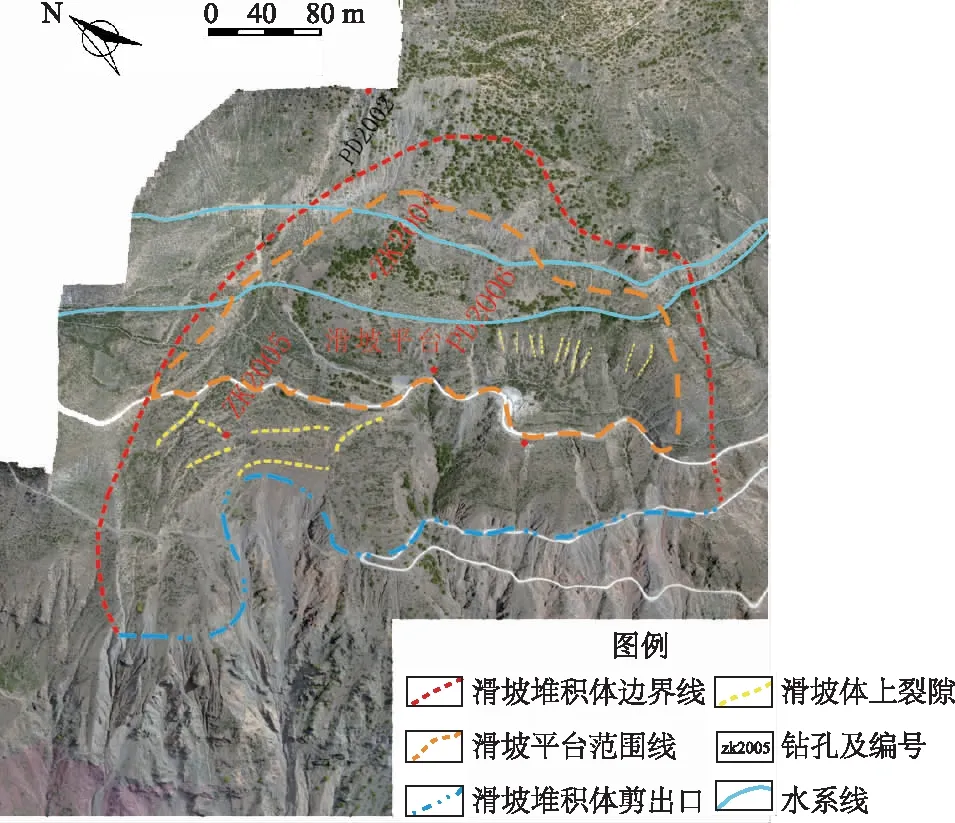
图1 滑坡边界特征Fig.1 Characteristics of landslide boundary

3 试验设计

针对以上滑坡堆积体裂隙发育特征，本文设计2组试验(均质型堆积体及裂隙型堆积体,均质型作为参考，模型尺寸为理想化，仅考虑实际堆积体中裂隙形状特征)来探究主-次裂隙对堆积体降雨入渗的影响。

3.1 试验装置

装置主要包括降雨系统、含刻度模型箱、摄相机及测量系统，其空间布置如图2所示。具体如下所述。

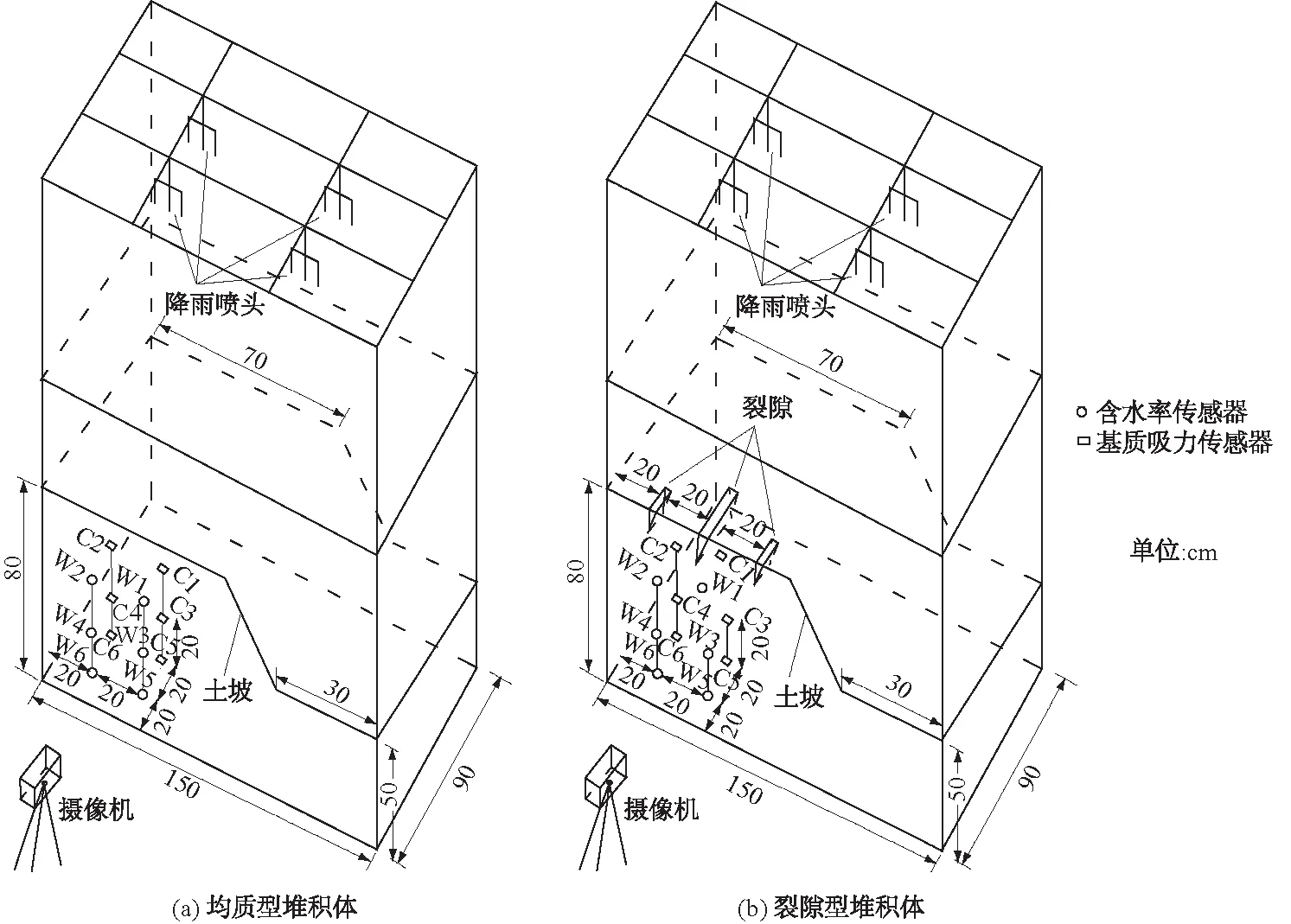
图2 试验模型示意图Fig.2 Schematic diagram of test models

(1)降雨系统：包括水管、压力表、水表及降雨喷头。通过改变水压及单位时间水流量来控制降雨强度。实测降雨有效面积为1.1 m2，雨强为18.6 mm/h。平均均匀度为80.1%。

(2)模型箱：长×宽×高为1.5 m×0.9 m×1.2 m。侧壁标有正方形网格(0.01 m×0.01 m)。

(3)测量系统：主要包括基质吸力采集系统及体积含水率采集系统各6套，分别为Campbel11257与CR1000数采仪及HCH2O-(EC-5)与Em50型自动数采仪。

3.2 试验材料

试验土体的选取至关重要，为使结果更符合实际情况，土体材料选自坡体后缘裂隙旁的堆积体。考虑到物理试验模型尺寸，利用等量替代法将粒径>4 cm的土粒重塑，其基本物理指标及粒径累计曲线见表2和图3。

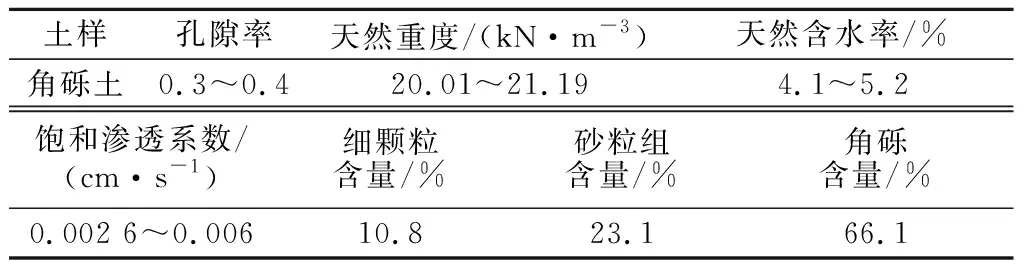
表2 土体基本物理指标Table 2 Basic physical parameters of soil

3.3 试验方案

试验分为2组(均质型堆积体和裂隙型堆积体)，裂隙是唯一控制变量。根据实地裂隙的整体发育尺寸及形态，本次试验主、次裂缝由带孔有机玻璃板替代，利用1∶100的相似比将主裂隙和次裂隙简化为“倒三棱柱”形状：主裂隙底宽3 cm，底长30 cm，高度25 cm，次裂隙底宽、底长和高分别为2、15、10 cm(图4)。2组试验坡体内部各布置6套体积含水率传感器(编号W1—W6)、基质吸力传感器(C1—C6)，布置位置见图2，裂隙中W1和C1位置稍有调整，其坐标为W1(40，20，50)、C1(40，25，50)，其余点位置相同。每组试验共经历4次降雨，每次降雨强度18.2 mm/h，累计降雨量与时间的关系见图5。试验过程中每间隔5 min对模型拍照，再结合模型箱上的刻度尺寸，读取湿润锋在各剖面上的迁移位置(图6)，最后整理出堆积体在降雨过程中湿润锋的运移速率及深度。

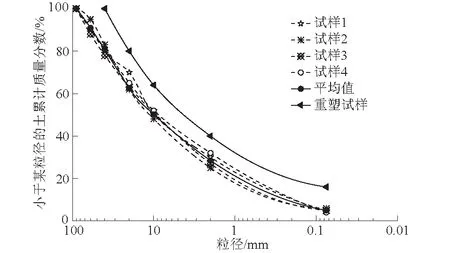
图3 粒径累计曲线Fig.3 Curves of cumulative particle size distribution

图4 土坡及裂隙布置Fig.4 Soil slope and crack layout

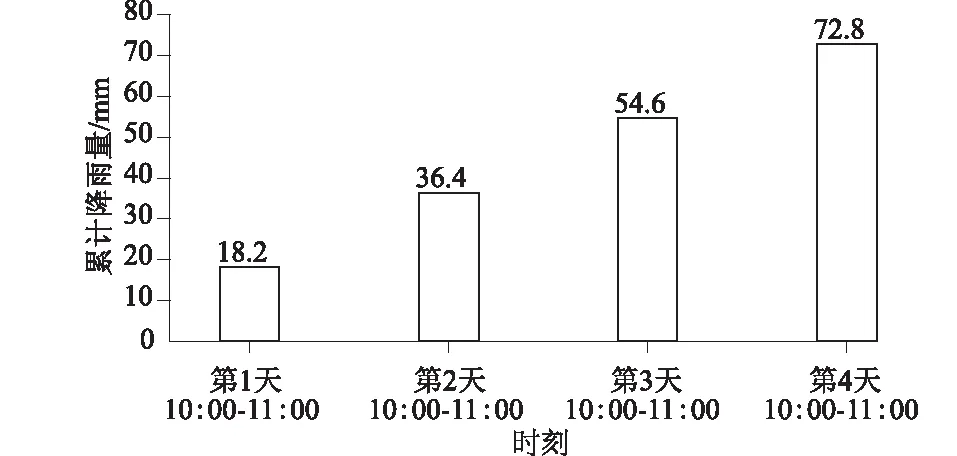
图5 累计降雨量与时间的关系Fig.5 Cumulative rainfall versus time

图6 湿润锋迁移位置Fig.6 Migration position of wetting front

4 试验结果与分析

4.1 降雨过程中含水率的变化

由图7可见，降雨开始70 min后，均质型堆积体中W1、W2(深度20 cm)测点迅速响应，含水率从0.055增加到0.18左右，随后由快至慢持续降低。而裂隙型堆积体中W1(深度30 cm)测点处含水率在降雨后50 min就快速增加到0.26，且与均质型堆积体埋设位置相同的W2测点也较均质型提前20 min响应。第2天降雨后，均质型与裂隙型堆积体中W3、W4(深度40 cm)也开始响应，但两者响应时间间隔约40 min，且最大含水率均较堆积体浅层(深度20 cm)小，裂隙型表现更加明显，相差0.14左右，降雨结束后，浅层堆积体的含水率消散速度比堆积体中部(深度40 cm)快。第3天，2种堆积体中W5、W6测点(深度60 cm)含水率也逐渐变大，裂隙堆积体中含水率达到峰值的时间较均质型快约1 h。第4天，均质型堆积体中底部测点含水率在降雨后几乎未有变化，与第3天降雨后一致，而裂隙型堆积体中同位置测点处继续增加，且达到最大值后降低幅度减小。值得注意的是，在裂隙型堆积体中，主裂隙正下方测点W1、W3、W5整体上均较次裂隙下方测点含水率增减趋势明显。

图7 体积含水率随降雨过程的变化Fig.7 Volumetric water content versus time

4.2 降雨过程中基质吸力的变化

均质型堆积体与裂隙型堆积体基质吸力变化整体趋势相当，均表现为雨水到达各测点后基质吸力迅速降低，随后保持不变，稳定在最小值。但是，由于裂隙的存在，每次降雨后2种堆积体所对应测点的响应时间有较大差异。第1次降雨后，均质型堆积体浅层测点C1、C2(深度20 cm)基质吸力变化响应较裂隙型堆积体C1(深度30 cm)、C2(深度20 cm)分别晚30 min及20 min。第2—第4天，裂隙型中部测点C3、C4(深度40cm)和底部测点C5、C6(深度60 cm)均较均质型快约30 min响应，且同一深度主裂隙正下方测点较次裂隙响应更快，如图8所示。

图8 基质吸力随降雨过程的变化Fig.8 Matrix suction versus time

4.3 入渗速率、深度与时间的关系

为了全面探索主-次裂隙对降雨过程中堆积体中湿润锋迁移速率与深度的影响，本次试验在均质型堆积体中选取3个截面进行观察，分别是L30(坡顶)、L90(坡腰)、L130(坡脚)，对裂隙型堆积体选取6个截面，分别是L10(次裂隙旁)、L20(次裂隙下方)、L30(主-次裂隙间)、L40(主裂隙下方)、L90(坡腰)、L130(坡脚)。其立面图及第1次降雨湿润锋的位置如图9所示，并根据图6所示的读取方式，整理出湿润锋的入渗速率及深度与时间的关系(见图10)。由于第3次降雨湿润锋已到模型箱底部，因此只讨论前2次降雨湿润锋的运移速率、深度。

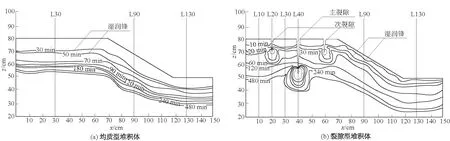
图9 湿润锋观测截面Fig.9 Observed positions of wetting fronts

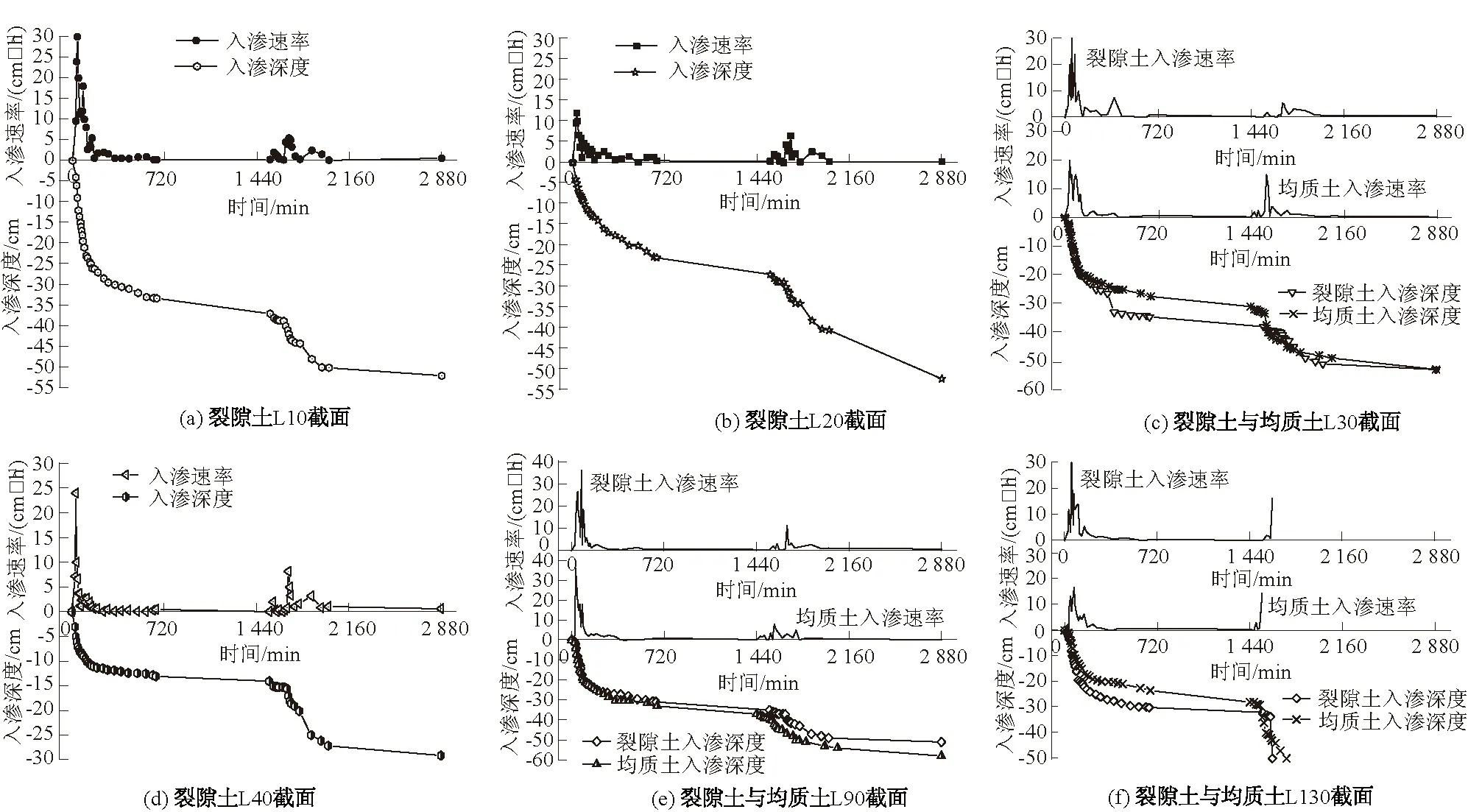
图10 堆积体入渗速率及入渗深度Fig.10 Rates and depths of infiltration in accumulation body models

(1)L10截面：降雨初期，裂隙型堆积体在L10截面入渗速率急剧增长，达到峰值30 cm/h。随着降雨的停止，速率迅速降低，期间个别时间段入渗速率上下起伏，整体趋势为入渗加速→峰值→入渗减速→趋向于0。第2次降雨较第1次明显不同，迁移速率最高仅为6.5 cm/h且上下浮动，降雨后9 h趋近于0；入渗深度规律与入渗速率完全吻合，第1次降雨入渗深度多达36 cm，但第2次降雨入渗仅16 cm。

(2)L20截面：该截面位于次裂隙正下方，降雨开始后10 min，底部已形成椭圆状湿润锋，前3 h的入渗速率较L10慢，峰值为12 cm/h。第2次降雨最大入渗速率较快，可达7.5 cm/h。2次降雨的入渗深度较为平均，每次约为27 cm。

(3)L30截面：对于均质型堆积体，降雨开始后，雨水入渗速率近直线上升，达到峰值20 cm/h后逐渐降低，8 h后趋于0，雨水入渗深度仅为27 cm。而对于裂隙型堆积体，该截面位于主-次裂隙之间，湿润锋最大入渗速率显著增加，为30 cm/h。但第2次降雨对其速率影响较小，最大值为6 cm/h。由于主、次裂隙底部湿润锋扩散的影响，8 h时，湿润锋深度达到35 cm。

(4)L40截面：截面位于主裂隙正下方，最大入渗速率为24 cm/h，降雨停止后，速率急速降低，8 h后雨水到达位置距坡表近40 cm，较未发育裂隙的土体入渗深度大。

(5)L90截面：该截面位于坡腰，均质型堆积体及裂隙型堆积体在第1次降雨中最大入渗速率均很高，达37 cm/h，最终入渗深度均质型较裂隙型多约8 cm。

(6)L130截面:该截面位于坡脚，裂隙型堆积体最大入渗速率为30 cm/h，而均质型堆积体仅18 cm/h，且到达箱底的时间不一致，裂隙型快约3 h。

5 数值模拟

5.1 数值计算方法

本文利用Geo-studio软件中Seep/W模块对裂隙型堆积体的降雨入渗过程进一步分析来探索裂隙对降雨入渗的影响。研究表明，土-水特征曲线是非饱和土入渗数值模拟的关键，徐绍辉等[14]认为Van Genuchten模型[15]无论是对黏质土还是对粗质土体均有较好的拟合效果。因此，根据实测的体积含水率及基质吸力和表达式(式(1))对土-水特征曲线进行拟合，其中土体的残余含水率参照涂国祥等[16]对角砾质碎石土的研究,拟合出的参数见表3。Van Genuchten模型表达式为

(1)

式中：θ为体积含水率；θs和θr分别为饱和含水率和残余含水率；α、n、m为模型参数；h为负压，取正值。

表3 堆积体土-水特征曲线参数Table 3 Parameters of soil-water characteristic curveof accumulation body

数值模型尺寸与室内降雨试验模型一致，长、宽、高分别为1.5、0.9、0.8 m，坡度为23.2°。降雨条件通过对土体表层施加单位流量来实现，模型共2 712个节点和2 625个单元，单元类型以四边形和三角形为主。常见的裂隙的处理办法目前有3种：一是将裂隙视为边界条件，其渗透性远大于周围土体，降雨时裂隙快速饱和[17]；二是将裂隙视为不同于土体的另一种均质材料，其渗透性较大且竖向渗透能力比水平方向大[18-19]；三是前2种方法的综合应用，裂隙深宽较大采用第1种处理，反之采用第2种[17-18]。考虑室内试验的情况，本文采用第2种方法，即将裂隙和土体分别赋值。由物理试验可得，4次降雨中，第1次降雨土体内部水分的运移最为典型，并且降雨持续阶段湿润锋迁移较明显，因此仅模拟1 d的降雨入渗过程，分析步时长为48 h，共48步，分析步时间采用指数增长。

5.2 数值模拟结果

数值模拟与室内试验所得部分湿润锋见图11，考虑到底部W5和W6测点第1天不会响应，因此仅布置4个监测点，所测的体积含水率见图7。

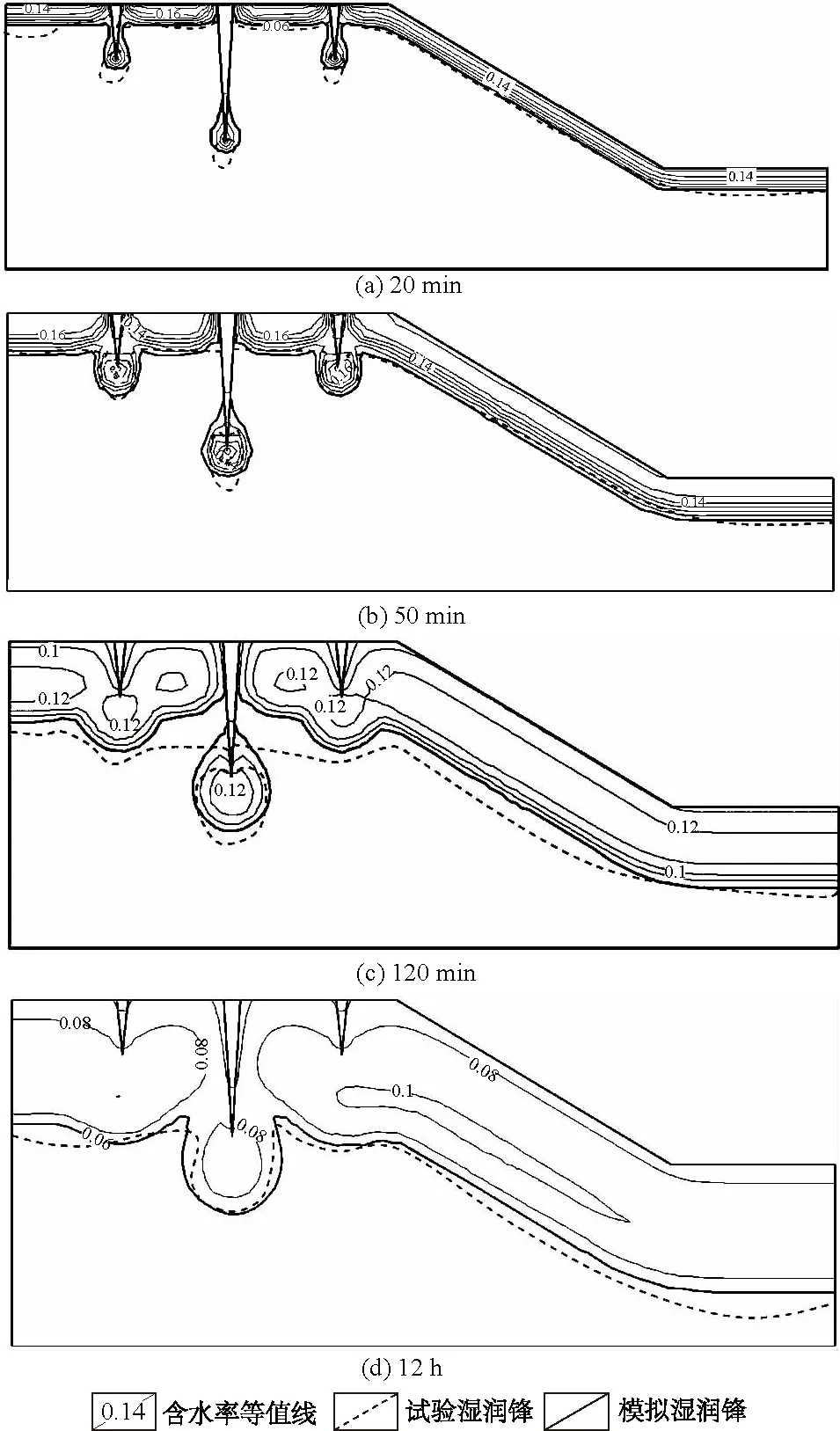
图11 室内试验与数值计算典型湿润锋Fig.11 Laboratory test and numerical calculationresults of typical wetting fronts

数值分析结果显示，降雨开始后，主裂隙正下方测点(距坡表深度30 cm)体积含水率50 min左右迅速增加，达到峰值0.16后由快至慢降低，而次裂隙正下方监测点(深度20 cm)体积含水率较主裂隙晚30 min响应，表明主裂隙的存在使雨水在相同时间入渗的深度更大。中部测点(深度40 cm)体积含水率在第2天降雨后60 min也逐渐增加，与室内试验增减趋势基本吻合。从湿润锋随时间的变化可知，降雨开始20 min，雨水通过裂隙快速到达土体深部，在裂隙底部周围形成椭圆状湿润锋，且越靠近裂隙其含水率越大。随降雨历程雨水持续下渗，且水平侧渗也逐渐加强，导致湿润峰扩散区域增大(50 min)。降雨开始后120 min，次裂隙下方与裂隙间土体湿润锋融会贯通，主裂隙上部两侧与下部周围土体湿润锋区域扩大，而中间两侧土体未受到雨水的浸湿。由于降雨结束，裂隙下方含水率较高区域的雨水继续入渗，补偿含水率较低的干土，受总降雨量的限制，入渗速度快速降低。12 h时，主、次裂隙湿润锋在土体中连成一片，且裂隙下方湿润锋深度较无裂隙处更大。室内试验与数值计算所得的湿润锋曲线虽有所出入，但整体趋势相同。

图12 典型湿润锋Fig.12 Typical wetting fronts

6 讨 论

结合室内降雨试验及数值模拟结果，降雨初始阶段，雨水不仅在土体表层入渗，且能通过裂隙到达土体内部，在裂隙周围形成椭圆状湿润锋，见图12(a)。降雨结束后，雨水在土体内部由快至慢继续运移。分析认为，裂隙的存在可以为雨水更快地渗透到土体深部提供优先路径，雨水使深层土壤含水率持续增加。当降雨持续一段时间后，靠近裂隙周围土体逐渐饱和，一旦降雨结束，暂态饱和区雨水继续渗入到周围干土中，补偿含水率较低区域，使土体中含水率均匀分布。第2次降雨后，部分土体中含水率较初始值高，对雨水下渗形成阻碍作用，再加上雨水继续补偿第1次降雨后含水率增加但未饱和区域，使雨水到达各测点的时间滞后，且除了主裂隙下方(L40)大部分截面的入渗速率明显下降。原因在于第2次降雨的雨水在裂隙中形成“水柱”(见图11)，在高水压力的作用下使裂隙下方土体加速下渗。值得注意的是第1次降雨后，裂隙中部两侧土体很长一段时间未受到雨水的浸湿，而仅在上部裂隙两侧和裂隙底部下渗，如图12(b)，结合均质型与裂隙型堆积体在L30截面(图10)的入渗速率和深度可知，裂隙具有一定角度，部分雨水沿裂隙壁往两侧水平入渗，使得在此截面入渗深度较大。

7 结 论

通过对均质型与裂隙型堆积体进行室内降雨试验和数值计算，并结合土体内部体积含水率、基质吸力及湿润锋的迁移速率的变化趋势，得到以下成果：

(1)裂隙型堆积体在降雨1 h和观测23 h的整个时间段内，其湿润锋迁移变化趋势可归纳为入渗加速→峰值→入渗减速→趋向于0。

(2)主-次裂隙的存在为降雨入渗提供了有利的渗流路径，雨水可快速渗透到土体深部，在裂隙周围形成暂态饱和区，降雨一旦停止，饱和区雨水将继续入渗，补偿其他区域。

(3)主、次裂隙之间在降雨过程中会相互影响，表现为裂隙间土体受两侧裂隙壁雨水的扩散其入渗速度和深度较大。裂隙下方和裂隙间土体湿润锋会相互贯通，在土体内连成一片。一次降雨后，内部含水量存在一个最大影响深度，达到该深度后入渗速率趋于0。

(4)降雨在裂隙型发育的堆积体中的入渗过程可分为4个阶段，即前期完全入渗(降雨开始1 h内)、裂隙下方强烈入渗(1～24 h)、补偿加速入渗(第2次降雨期间)及水平侧渗(6 h—试验结束)。

本文仅考虑了裂隙发育形态对降雨入渗的影响，成果可为进一步探讨在强降雨作用下堆积体中裂隙发育是否会诱发深层滑坡提供参考。