粒子释放与速度动态变化的改进粒子群算法
马欣 闫莉
(西安工业大学机电工程学院 陕西省西安市 710021)
粒子群算法(PSO)是Kennedy[1]等人于1995年受鸟群捕食行为启发而提出的一种基于群体行为协作的随机搜索算法。粒子群算法具有算法原理简单易理解、参数少、算法收敛快、鲁棒性好、且易于程序实现等优点,并适用于很多工程实践问题;因此,PSO 自提出以来受到众学者的关注。PSO 已经在自动化技术、神经网络训练、电力工业优化、参数辨识等诸多领域得到了广泛应用。多年来,针对PSO 的研究成果众多。
经阅读文献[2-23]并对其总结可知对PSO 的改进大致包括以下几方面:
(1)对初始种群的产生方法的改进;
(2)对PSO 自身的参数进行改进;
(3)对粒子邻域拓扑结构的改进。
粒子群算法的收敛性和多样性之间的矛盾关系是:如果粒子快速收敛,将不可避免地导致粒子的逐渐同一性,从而限制了粒子的搜索范围,并且算法容易陷入局部最优。如果增加了粒子的多样性,打破此限制以扩大搜索范围可以改善粒子落入局部最优的情况,但同时也会降低算法的收敛速度,甚至可能出现结果发散和计算误差增加的现象。根据文献研究,如果要平衡两者之间的关系,当前有效的解决方案是在算法的早期阶段增加粒子的多样性,以便可以在更大的搜索范围内搜索粒子;在算法的后期,粒子速度不断变化以减少每个粒子对全局最优解位置的搜索次数提高了算法的后期收敛性。
为改善标准粒子群算法的不足,本文提出一种粒子释放与粒子速度动态变化的改进粒子群算法(PR&SDC-PSO)。测试结果表明PR&SDC-PSO 可以改善标准粒子群算法收敛慢、搜索精度低、易陷入局部最优等缺点。
1 粒子群算法原理
标准粒子群算法是基于对鸟类群觅食行为的研究。它是对群体行为的模型抽象,并用于解决实际的优化问题。标准粒子群算法的优化过程可以描述为:每个粒子通过判断其自身的历史最佳位置和其他个体的历史最佳位置以及连续迭代的总体趋势来连续调整其下一个搜索速度和位置。
假设在D 维搜索空间中有一组N 个粒子,则t 代的第i 个粒子的位置可以表示为:

粒子速度可以表示为:

那么,第t+1 代第i 个粒子速度与粒子位置的第d 维,可以按式(3)和(4)进行更新。
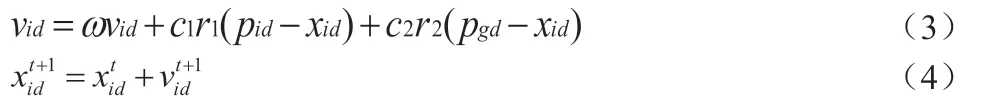
其中:i=1,2,…n,d=1,2,…D;ω 为惯性权重;c1 和c2 为学习因子,是非负常数;r1 和r2 为(0,1)内均匀分布的随机数;pid和pgd分别表示个体最优位置和种群全局最优位置;vmax是常数。
2 粒子释放—速度动态变化的粒子群算法
为了有效地提高PSO 性能,提出粒子释放[7]和粒子速度动态变化的结合策略,实现当算法陷入局部最优时增加粒子的多样性,当粒子过于发散提高算法的收敛性的综合效果。用于释放粒子的条件是:当检测到最佳适应度值在设定的迭代步数内没有更新时,该算法将被判断为陷入局部最优。在这种情况下,当前的最优粒子全局搜索能力差。为了改善目前的停滞状态,释放粒子到搜索的空间边界,以增加粒子的全局搜索潜力附近,粒子释放公式为:

其中:xid 与vid 为粒子i 第d 维的位置与速度,ud 为第d 维空间的上限,ld 为第d 维空间的下限。
释放粒子后,如果在一定数量的迭代步数中检测到最佳适应度值没有更新,则算法将再次执行粒子释放操作。为了在增加粒子多样性的同时确保算法的最终收敛效果,有必要避免发生粒子的释放速度大于粒子的收敛速度的情况。因此,引入速度动态变化策略是为了使释放的粒子迅速再次收敛到最优种群附近,从而确保算法的最终收敛效率。
在PSO 中存在粒子最大速度vmax来限制粒子运动步长,粒子i第d 维的速度若vmax值过大,粒子可能会越过优质搜索区域,降低搜索精度;如果vmax值过小,那么粒子的搜索慢,导致其收敛性较差。为了改善vmax值对PSO 影响,本文提出粒子的速度动态变化策略,粒子速度可以设置为:

上式中:v'max与v'min为极限最大、最小速度限制;T 为最大迭代代数。可以看出v'max、v'min根据迭代次数从1.0 线性递减,该策略使粒子在算法初期全局范围内搜索,在后期可以使粒子在局部区域重点搜索,避免粒子释放出去以后迭代过慢。从而加快算法收敛,提高算法性能。
3 算法步骤
基于粒子释放与速度动态变化改进后的算法(PR&SDC-PSO)步骤如下,用K 来判定是否进行粒子释放操作。
(1)粒子群初始化。设定初始粒子群的规模,随机生成粒子的位置和速度,其中
(2)计算每个粒子适应度值,并更新每个粒子的个体历史最优位置和种群历史全局最优位置,令K=0。
(3)按照式(6)计算各个粒子的最大速度。
(4)根据式(3)(4)更新粒子速度与粒子的位置。xid如果超出了位置限制边界,则将其位置设置为相应的边界值。
(5)再次计算每个粒子的适应度值,并更新每个粒子的个体最优和种群全局最优。
(6)若全局最优有更新,则K=0;否则K=K+1。
(7)若K=m 时,并按式(5)释放最优粒子。
(8)若没有到达事先设定的最大迭代数则返回步骤(3),否则迭代停止。
4 测试函数
为了衡量改进后的算法的可行性与有效性,本文选取了三个测试函数用于算法测试。
4.1 Schaffer函数
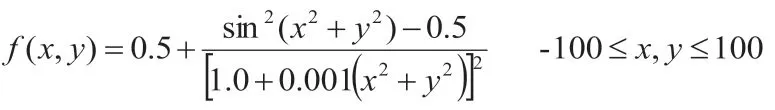
Schaffer 函数是一个多峰函数。此函数包含无限数量的局部极值和全局极值,搜索难度很高。它通常用于验证算法的搜索准确性,全局最小值为f(0,0)=0。全局最小值解周围有无数的局部最小值解,因此很难寻优。Schaffer 函数图像如图1所示。
4.2 Girewanks函数

该函数是单峰函数,全局最小值为f(0,0)=0。此函数的搜索难度较小,通常用于验证算法的搜索效率。Girewanks 函数图像如图2所示。
4.3 Ackley函数
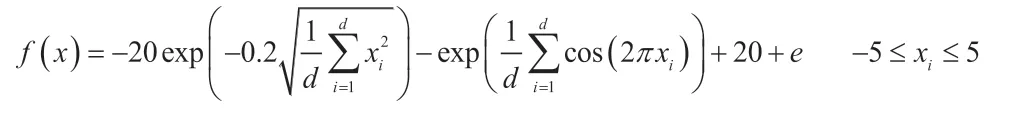
Ackley 函数是一种激烈的多峰函数。该函数更复杂,并且具有多个局部最小值,因此很难搜索全局最优值。Ackley 函数图像如图3所示。
5 仿真实验与性能分析
针对不同算法性能对比,将不同算法的参数统一设置为:粒子数量n=25,允许最大迭代次数1000 次;惯性权重采取随时间变化的策略,惯性权重从0.9 线性递减,达到最大迭代次数时降至0.4;学习因子c1、c2都设定为1.8。每种算法经过200 次测试,结果如表1所示。

图1:Schaffer 函数图像
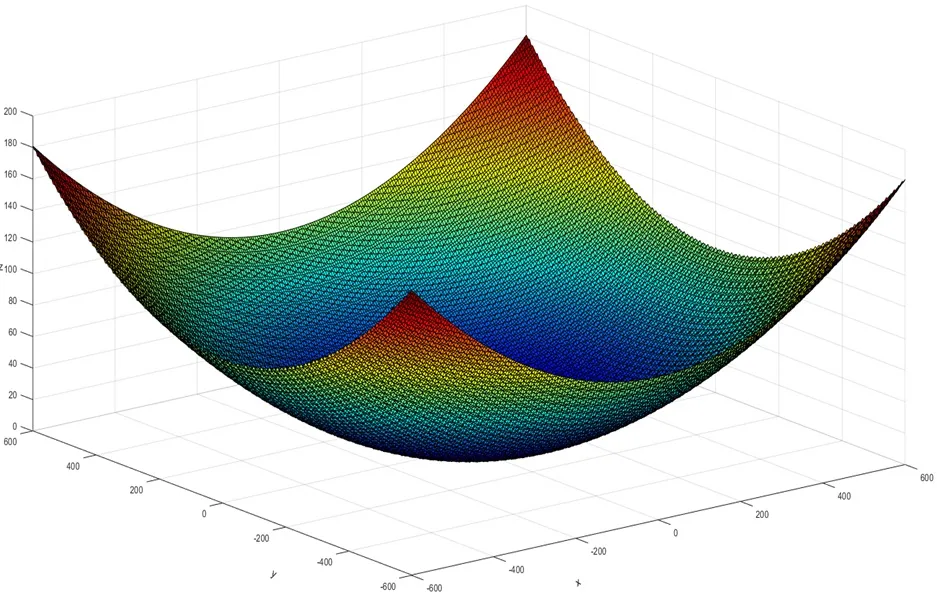
图2:Girewanks 函数图像
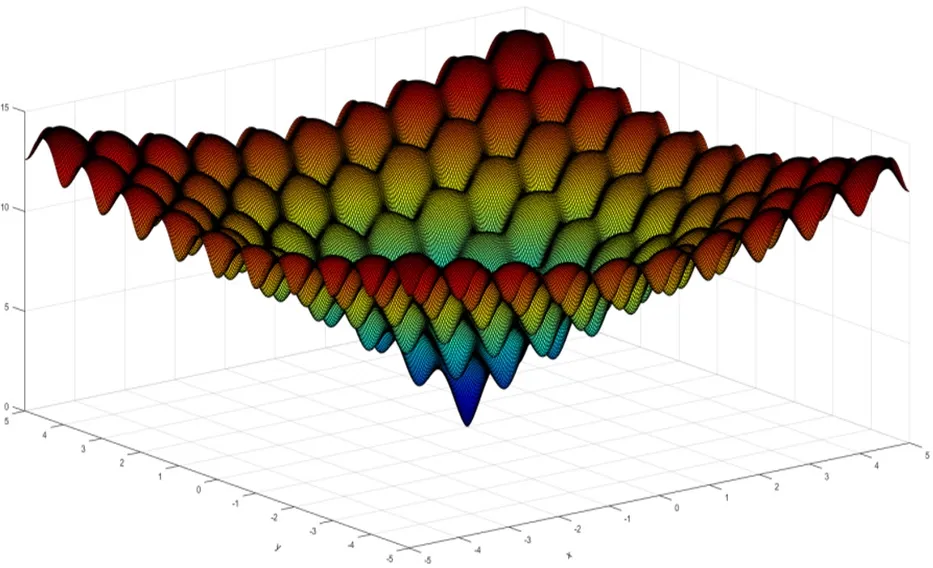
图3:Ackley 函数图像
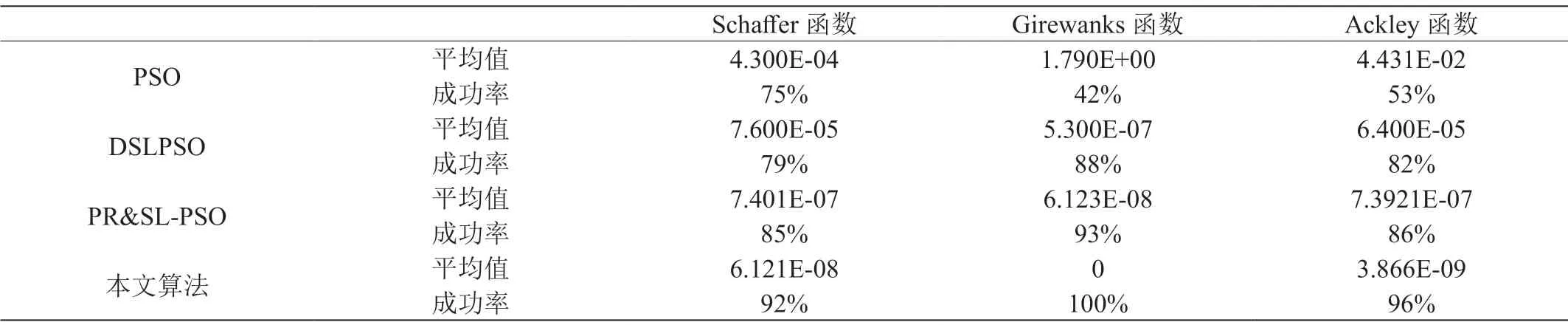
表1:测试结果
对比分析表1的测试数据可知,表1中本文改进后的PR&SDC-PSO 的寻优性能是所列算法里最好的。对于Girewanks函数这个单峰函数来说,PR&SDC-PSO 求得了最优值且收敛较快,说明该算法的搜索能力强。而对于另外两个激烈的多峰函数而言,在寻优时均取得比其他算法更精确的最优值;与其他算法相比PR&SDC-PSO 算法具有更好的性能,验证了改进方法的可行性与有效性。
6 结束语
针对标准粒子群算法的过早收敛以及后期搜索收敛的精度低的问题,提出了一种改进的粒子释放-粒子速度动态变化策略。将Schaffer 函数,Girewanks 函数和Ackley 函数用作测试函数,以测试改进算法的有效性,并对结果进行分析和比较。分析结果表明,引入改进的粒子释放和粒子速度动态速度变化来改进粒子群算法具有明显的优势。

