混沌系统的变时刻脉冲控制与同步
2021-04-20 02:23胡茂萍
电子技术与软件工程 2021年2期
胡茂萍
(重庆师范大学数学科学学院 重庆市 401331)
非常多的非线性系统在参数和初始值满足一定条件下就会出现混沌吸引子,具有混沌吸引子的系统是比较难控制的,于是一大批学者对混沌系统的控制问题进行深入研究,他们提出了许多控制方法来镇定混沌系统的状态曲线,比如时滞反馈控制,自适应控制,脉冲控制等方法[1-3],其中脉冲控制方案只需对系统进行不连续的控制,具有成本低的优势,被很多学者所采用,比如文献[4-6],但上述文献都设定脉冲量在固定时刻注入系统,而在实际的环境中,由于多因素的影响,脉冲量很难在固定时刻注入系统,脉冲量完全可能在一个时间区间内的任意时刻注入系统,故讨论混沌系统在变时刻脉冲控制下的行为具有更实际的意义。文献[8]的作者研究时滞线性系统在变时刻脉冲控制下的一致稳定问题,文献[9]的作者利用变时刻脉冲控制协议研究了非线性多智能体系统的一致性问题。
1 混沌系统的变时刻脉冲控制
一类n 维混沌系统如下

为了方便书写,后面均将x(t)简写为x,有变时刻脉冲控制器的混沌系统(1)为:
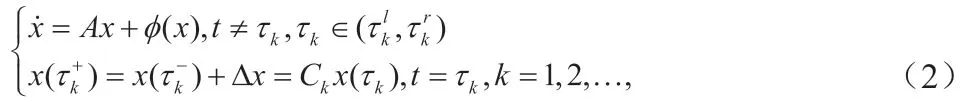
定理1 假设q 是(AT+A)的最大特征值,q+1+L2=p,dk是的最大特征值,如果存在常数ξ>1 满足

则有变时刻脉冲控制器的系统(2)渐近稳定。

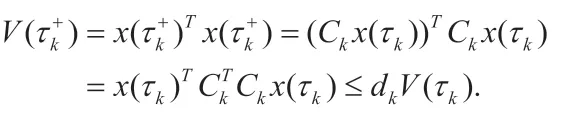

推论1 假设q 是(AT+A)的最大特征值,q+1+L2=p,dk是的最大特征值,如果存在常数ξ>1 满足则变时刻脉冲控制下的混沌系统(2)渐近稳定。
2 混沌系统的变时刻脉冲同步
在同步模型中,驱动系统为

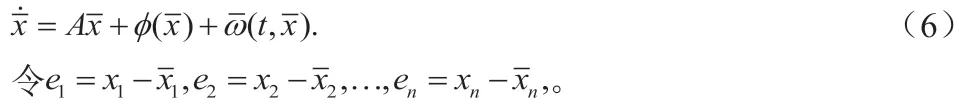
那么误差系统为

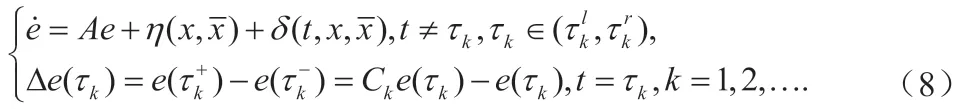

则系统(5)与(6)实现鲁棒同步。
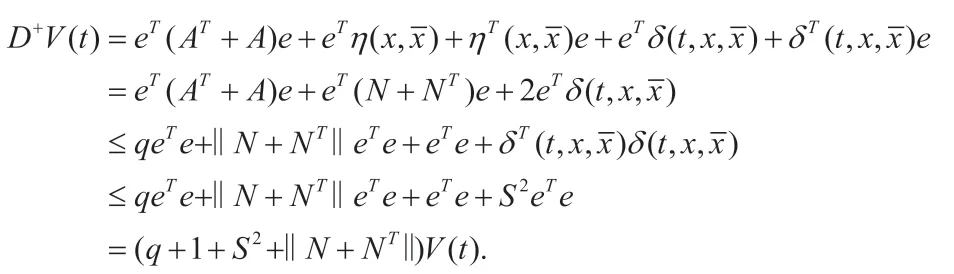
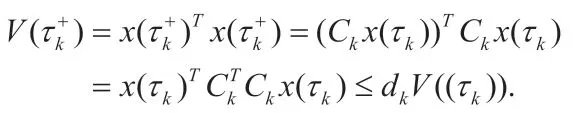
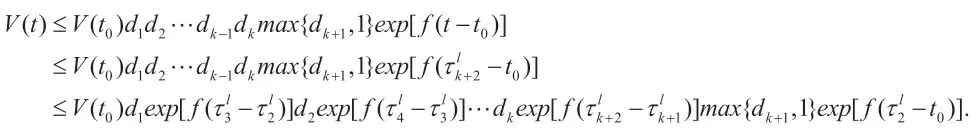
3 数值实验
考虑一个三维混沌系统如下


其中
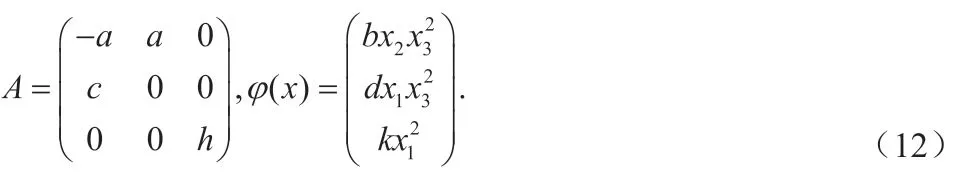
响应系统为


图1:误差系统的状态曲线
猜你喜欢
数学物理学报(2021年5期)2021-11-19
数学年刊A辑(中文版)(2021年1期)2021-06-09
烟台大学学报(自然科学与工程版)(2021年1期)2021-03-19
数学物理学报(2020年5期)2020-11-26
山西大同大学学报(自然科学版)(2016年4期)2016-11-27
东北电力大学学报(2015年1期)2015-11-13
四川师范大学学报(自然科学版)(2015年2期)2015-02-28
应用数学与计算数学学报(2014年3期)2014-09-26
四川轻化工大学学报(自然科学版)(2014年3期)2014-04-16
云南中医学院学报(2012年3期)2012-07-31

