凸轮连杆组合机构解析法设计

蒋志华， 贺兵， 敬宏图， 刘忠伟

（湖南工业大学机械工程学院，湖南株洲412008）

0 引言

目前已有了许多对凸轮连杆组合机构的研究成果，但在已发表的文献资料中，还未能见到图1所示末端从动件按一定规律往复运动的凸轮连杆组合机构基于解析法的具体设计。

在凸轮连杆的设计中，凸轮轮廓曲线设计的优劣直接影响了凸轮连杆机构的稳定性，因此凸轮轮廓曲线的设计成为研究重点。常用的凸轮设计方法有解析法和图解法，图解法设计精度低的说法是针对传统的图解法而言的，但利用仿真软件辅助设计时，则具有精确度高、设计周期短等优点[1～3]。如张磊[4]利用Adams设计滚子从动件凸轮轮廓曲线，郑彬利[5]用AutoCAD与Excel设计凸轮轮廓曲线，黄文权[6]利用Creo对凸轮机构进行反转设计，王亮[7]采用图解法利用SolidWorks设计滚子盘形凸轮机构。

利用仿真软件的图解法，能够得到精确的凸轮轮廓，但是只能对某一固定参数的机构进行设计，当机构参数发生改变时，需要利用仿真软件重新建立模型求解，并且不能对凸轮压力角进行检验。基于上述原因，本文采用解析法并借助MATLAB对图1所示凸轮连杆组合机构进行设计。解析法可以对凸轮轮廓曲线的坐标值进行精确的计算，当从动件运动比较复杂，计算复杂时，用MATLAB软件可以很容易地进行凸轮轮廓曲线的解析法设计[8]。

1 凸轮连杆机构设计方法

1.1 凸轮连杆组合机构工作原理

凸轮连杆组合机构如图1所示，凸轮为主动件绕C点逆时针方向旋转，AD杆上B点处的滚子在凸轮槽中滚动，并带动AD杆绕A点摆动，AD杆通过连杆DE使滑块按一定的运动规律上下往复运动。在实现相同滑块行程和运动规律的条件下，凸轮连杆机构的凸轮和压力角比单凸轮机构的小得多[9]，因此图1所示凸轮连杆组合机构在末端执行部件按一定运动规律往复运动的机械中具有十分重要的工程意义。

1.2 参数确定

如图2所示，以C点为原点，过C点的水平线为x轴，过C点的垂直线为y轴，垂直xy平面向外为z轴建立坐标系。已知参数：C点坐标，A点坐标，AB的长度，BD的长度，DE的长度，滑块在最高点时E0点的坐标，滑块从最高点开始下降的距离为S，最高点到最低点的距离即行程为SM。

滑块在运动的过程中，E点的纵坐标yE=yE0+S。设AE=L，AB=a1，BD=a2，θ为AD和x轴的夹角，β为AE和过A点做平行于x轴的直线的夹角。滚子中心点和凸轮理论轮廓的交点为B。确定好设计参数之后便可进行设计理论公式推导。

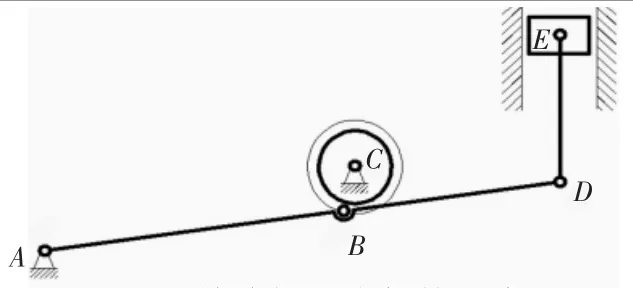
图1 凸轮连杆组合机构示意图

图2 凸轮连杆组合机构的结构简图

1.3 凸轮轮廓设计

1.3.1 凸轮轮廓极坐标极径的确定

由两点间的距离公式得：

求得B点的坐标后，便能求得凸轮轮廓曲线极坐标的极径r。需再求得极径对应的极角才能求得凸轮的理论轮廓曲线。

1.3.2 凸轮轮廓极坐标极角的确定

如图3所示，当凸轮转过角度φ2时，凸轮相对于B点处滚子转过的角度为φ1。由图3可知φ1显然不等于φ2，在求解凸轮轮廓曲线时是利用B点的运动轨迹进行求解，所以我们需要求得凸轮相对于摆杆上滚子转过 的 角 度φ1，求解过程如下。

图3 凸轮转角

则凸轮相对于摆杆上滚子转过的角度为

式（11）中出现了“±”，故须按以下两种情况确定：1）当AB杆与BC所成连线的夹角小于90°时，如果AB杆转动方向与凸轮转动方向相同为减，相反为加；2）当AB杆与BC所成连线的夹角大于90°时，如果AB杆转动方向与凸轮转动方向相同为加，相反为减。

1.4 检验压力角

设计凸轮机构时，除了要求从动件能实现预期的运动规律外，还希望凸轮机构结构紧凑，受力情况良好，而这与压力角有很大关系。因此无论凸轮机构中压力角α是一个重要参数[10]，当机构中压力角α较大时，会导致导路中摩擦阻力大于有用分力，因此凸轮加给从动件的作用力多大，从动件都不能运动，这种现象称为自锁。在计算凸轮压力角时，由于摆动从动件回程的许用压力角[α]较大（70°～80°），不需要检验回程压力角，所以只需要计算推程压力角，并保证其不超过许用值。

如图4所示，凸轮的压力角α1为滚子中心所做理论轮廓线的法线n-n与AB杆的运动方向线之间的夹角。设AB杆的运动方向线的斜率为k1，法线n-n的斜率为k2，与法线n-n垂直的直线斜率为k3，由2条相互垂直的直线的斜率相乘为-1得：

图4 凸轮压力角

应保证α1的最大值不超过许用值，即α1max＜[α1]，可取[α1]=45°。

应用MATLAB编程计算，求得凸轮推程压力角最大值α1max，检验是否符合要求，如果不符合要求则需重新设计。

1.5 利用Adams对比验证

在Adams中建立凸轮连杆模型，并给予滑块一个驱动，设置滑块的运动规律，然后通过连杆带动摇杆摆动，再在凸轮转动中心设置一个转动的正方体，转动的正方体必须能使滚子在范围内，通过描点的方式使凸轮的理论轮廓线刻画在转动的正方体上，从而得到轮廓线，将Adams中凸轮理论轮廓曲线的数据点导出，用文本文件保存并导入MATLAB中，然后再用MATLAB编程算得的轮廓线进行比较，如果两者重合，则证明MATLAB编程的轮廓线为正确的。

2 数值算例

2.1 参数确定

图2所示的凸轮连杆组合机构，根据整体工艺要求，已知在凸轮的一个转动周期中，从动件需实现1次升降、2次暂歇。各个连杆的长度由整体结构可确定。已知参数：C点的坐标为（0，0，0），A点的坐标为（-371.65，-70，0），AB的长度a1=365 mm，BD的长度a2=325 mm，DE的长度为160 mm， 滑 块 在 最 高 点 时 ，E0点 的 坐 标 为（318.63440706，109，0），滑块从最高点开始下降的距离为S，根据实际需求，滑块的行程SM=38 mm。

2.2 末端从动件运动规律

滑块运动规律为：下降→暂歇→上升→暂歇。设凸轮的转过的角度为φ，已知凸轮的升程角φ1=40°，近休止角φ2=140°，回程角φ3=40°，远休止角φ4=140°。

为减少刚性柔性的冲击，本机构采用凸轮的多项式运动方程进行求解，在第一段和第二段连续下降的过程中只需要考虑位移，速度和加速度连续即可，第一段下降可以采用三次多项式方程，而第二段需采用五次多项式方程。在升程角这段，为方便更改数据，设计计算压力角的大小，第一段升程采用五次多项式运动方程，第二段也采用五项式运动方程。

根据表1和已知参数利用MATLAB进行辅助计算，求出滑块运动规律方程。

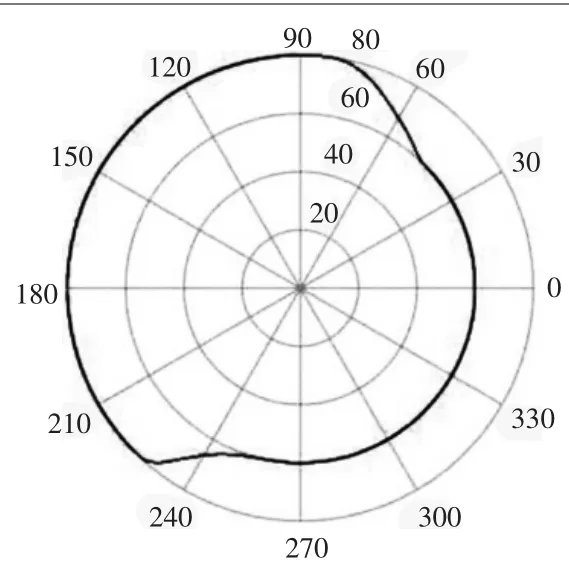
图5 凸轮理论轮廓曲线

图6 凸轮升程压力角

表1 位移分配表

2.3 凸轮轮廓设计

根据求得的运动规律方程及式（1）～式（11），应用MATLAB进行编程计算，求得凸轮轮廓曲线坐标，并画出凸轮的理论轮廓曲线，如图5所示。

2.4 检验压力角

应用MATLAB根据式（12）～式（15）进行编程计算，求得该凸轮推程压力角最大值为α1max=36.1301° ，符合要求，如图6所示。

2.5 利用Adams对比验证

已知滑块的运动规律为多项式运动规律，用滑块带动连杆运动，即反转法得出凸轮轨迹。首先建立连杆及滑块模型，给予合适的约束。然后给滑块一个上文中所求得的多项式运动规律。随后在凸轮的绕转中心位置创立一块正方形板，给正方形板一个绕其中心以-360.0d *time的转速转动的运动。最后进行仿真得到凸轮理论轮廓线轨迹如图7所示。

将Adams中的理论轮廓线的数据点导入MATLAB，与MATLAB编程算得的轮廓线进行比较，凸轮轮廓对比如图8所示。

结果显示，二者轨迹完全重合，证明求解理论过程正确。

图7 Adams仿真

图8 凸轮轮廓线对比

3 结语

1）为了解决凸轮连杆设计中末端从动件按一定运动规律往复运动的凸轮连杆组合机构的设计问题，采用解析法对图1所示凸轮连杆组合机构进行求解，并推导出该凸轮连杆组合机构的设计理论公式。

2）利用MATLAB和Adams验证了设计理论公式的正确性，并借助MATLAB强大的数值计算能力，方便得到了凸轮轮廓曲线，并对其压力角进行了检验。

3）在凸轮连杆组合机构的求解方法中，解析法对于快速求解某一类凸轮连杆组合机构更具优势，采用解析法推导出该类凸轮连杆组合机构的设计理论公式之后，利用MATLAB对设计理论公式进行编程，在求解同种类型的凸轮连杆组合机构时只需调用程序，并修改相关设计参数便能快速求得需要的凸轮轮廓曲线。