稳健波束域MVDR 高分辨算法

魏涛 沈文苗

（第七一五研究所，杭州，310023）

用声基阵探测目标时，传统的方法采用常规波束形成（Conventional BeamForming，CBF），但是它的方位估计精度和分辨能力较差，特别是在低信噪比下，当多个目标方位互相靠近时，CBF 算法的分辨能力就显得很有限。针对这一局限性，Capon于1969 年提出了具有良好的分辨能力的MVDR 波束形成器[1]，但是该算法对阵列失配敏感，在阵列校准失配、快拍数少等情况下，性能严重下降。

现在已有许多方法来提高MVDR 算法的稳健性[2-7]，其中包括NCCB 和RCB[4]，它们都属于对角加载法。NCCB 根据阵列失配程度利用加权范数约束来自适应地求解加载量；RCB 利用阵列导向矢量的不确定集求解加载量。然而NCCB 和RCB 在运算过程中计算量都较大，在实际工程中难以应用。为了降低计算量，文献[8]提出在RCB 框架下的Krylov子空间降维技术，以实现低复杂度且快速收敛的稳健自适应波束形成器。文献[9]提出通过划分子阵的方式来进行降维处理，以牺牲一定的分辨率来减小算法的复杂度，具有一定的工程应用价值。

本文利用波束域降维方法，即将阵元域数据转换成低维的波束域数据，再进行后续处理；理论推导了BNCCB 和BRCB 算法，经仿真分析结果验证了其运算速度和算法稳健性均得到提高。

1 算法描述

1.1 MVDR 算法

假设基阵是由M 个水听器组成的均匀线列阵，阵元间距d 为半波长，且空间存在l 个远场无关的窄带信号入射进基阵，如图1 所示。

假设信号入射的方位角为 θi（ i=1,2, … ,l），则相邻阵元之间的时延表示为

式中，c 为水声信号的传播速度。

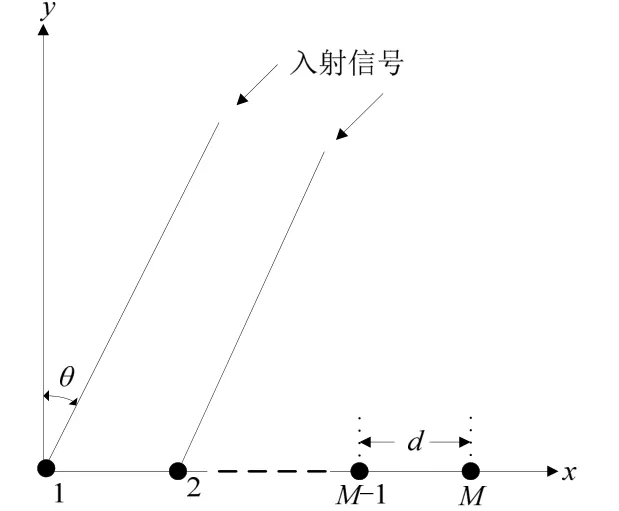
图1 基阵结构示意图

对于阵元间距为半波长的均匀线阵，阵列的导向矢量为

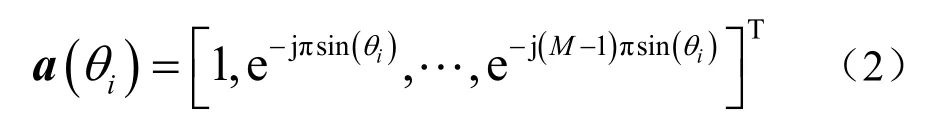
则阵列流形矩阵表示为

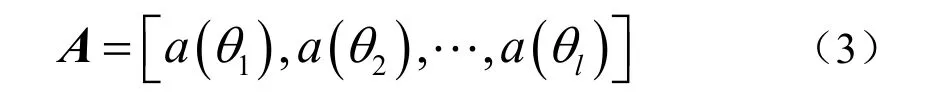
窄带远场信号的阵列接收数据模型为

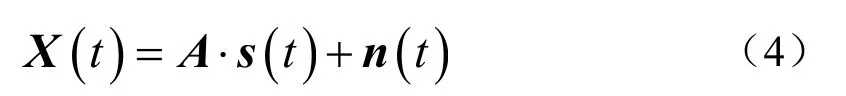
式中， s （ t ）是信号向量， n （ t）是噪声向量。

在实际中，阵列协方差矩阵ˆR 是未知的，可以由一段数据快拍样本的空间相关矩阵来估计：

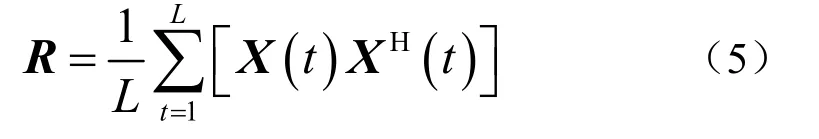
式中，L 是快拍数，（）H· 表示共轭转置。

MVDR 波束形成器的设计原理是让它对感兴趣方位的信号无失真地输出，而使波束输出功率P =wHRw 最小。即

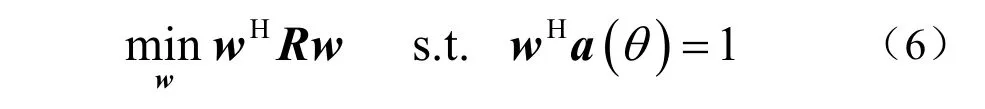
采用拉格朗日算子，可求得MVDR 波束形成器的权矢量为

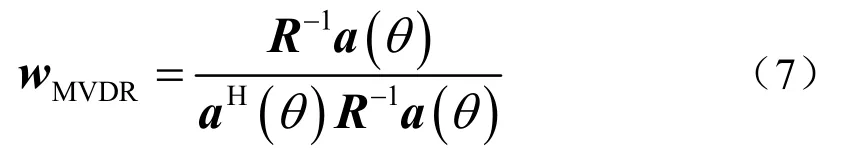
则MVDR 波束形成器在观察视区Θ（θ ∈Θ）扫描的输出功率为

1.2 BMVDR 算法

波束域方法将阵元空间数据转换到波束空间，如图2 所示，这一步是波束域方法的关键[10]。以半波长布阵方式，由M 个阵元组成的均匀线阵的离散空间傅里叶变换可表示为

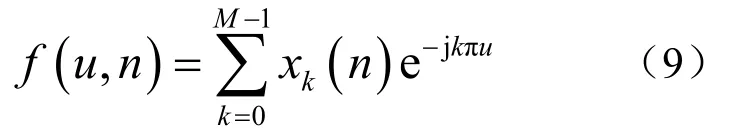
式中，sinuθ=。

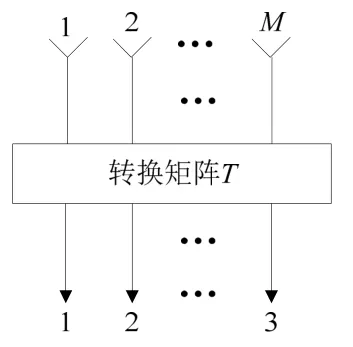
图2 空间转换示意图

定义1M× 的离散空间傅里叶变换波束形成加权矢量为

并构造M N× 的波束转换矩阵T 为

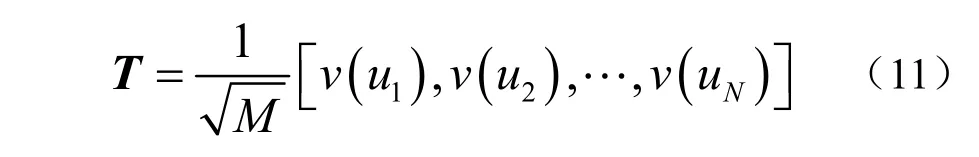
为了保证波束转换后不改变噪声的统计特性，使波束域输出仍然满足空间白噪声背景，通常要求波束转换矩阵满足

不满足上式时，可以通过To=T （THT）-1/2进行正交化。此时波束域中输入向量表示为

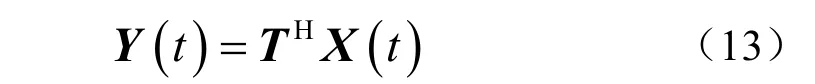
波束域中导向矢量表示为

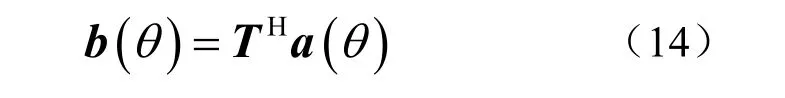
而波束域输入向量的协方差矩阵为

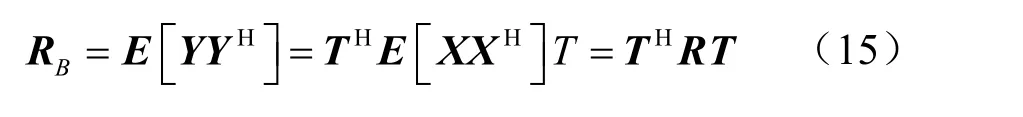
因此，BMVDR 的权矢量表示为

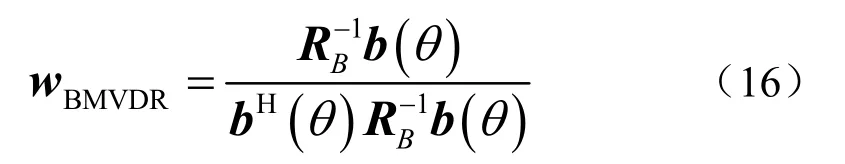
则BMVDR 波束形成器在观察视区Θ（θ∈Θ）扫描的输出功率为

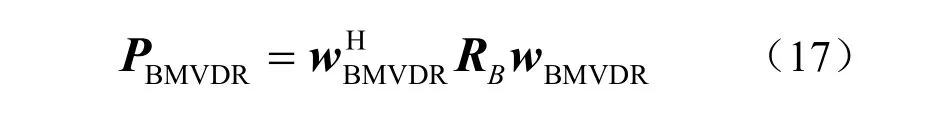
1.3 BNCCB 算法

对BMVDR 波束形成器增加加权向量范数，得到BNCCB。

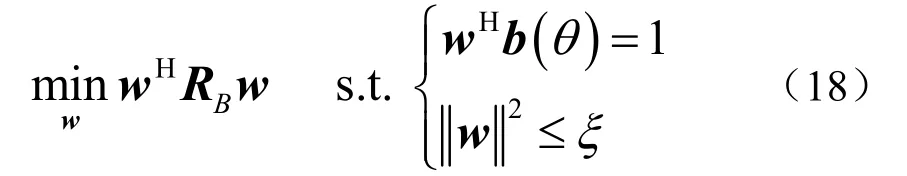
式中，ξ 越小，波束形成器的稳健性越高。但它不能无限小，还须满足1/Mξ ≥ 。

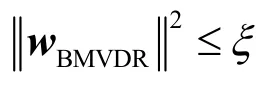
因此，若范数约束是激活的，BNCCB 波束形成器为

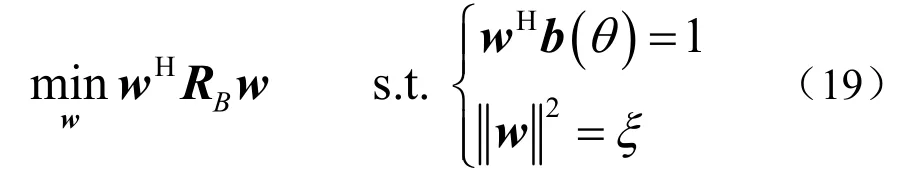
利用上式约束条件，通过拉格朗日算子可以求得BNCCB 的权矢量为

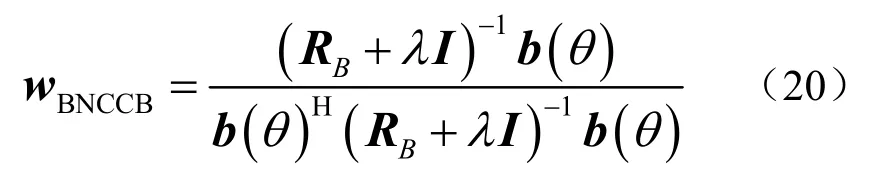
可见，BNCCB 波束形成器属于对角加载类方法。与常规对角加载法不同的是，BNCCB 波束形成器中的对角加载量是通过加权向量范数约束量确定的。

BNCCB 波束形成器对角加载量λ 可以通过求解如下方程得到

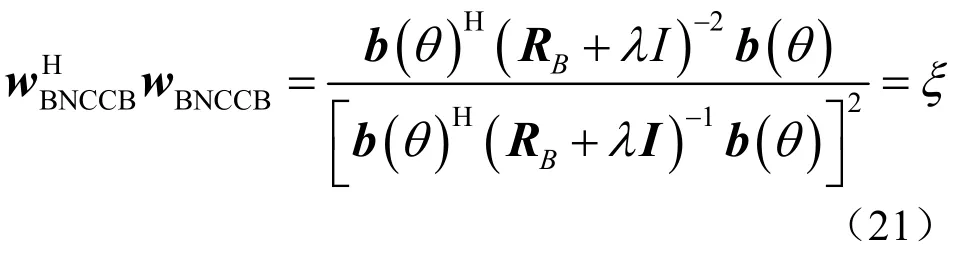
可以证明[11]，在激活条件约束下，上式存在唯一的正数解0λ ＞ 。而且式（21）左边函数是单调降函数，因此可以用牛顿迭代法求解。接下来求λ的范围。将BR 进行特征值分解，得到

式中，BΓ 是由特征值组成的对角矩阵，且

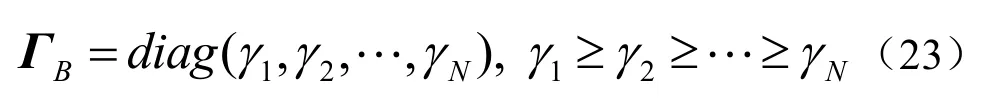
令

且nz 表示z 的第n 个元素。式（21）可以写成[6]

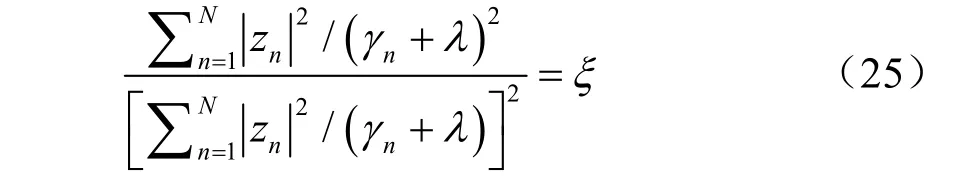
因此有

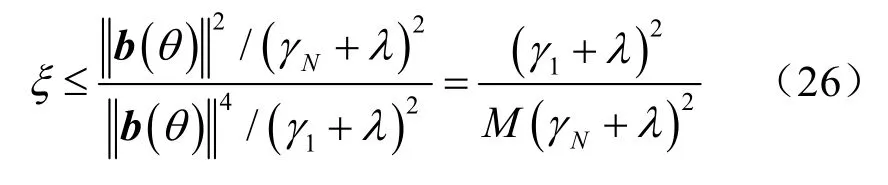
由此可以得到λ 的上界，考虑到0λ ≥ ，λ 的上下界范围为

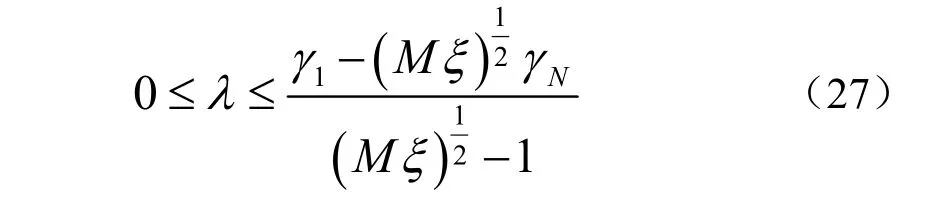
将求解出的λ 代入到式（20）中得到 wBNCCB。

BNCCB 波束形成器在观察视区Θ（θ∈Θ）扫描的输出功率为

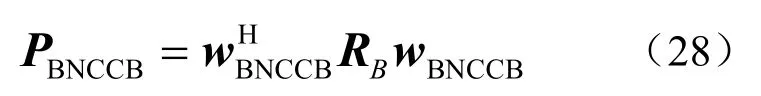
波束域数据协方差矩阵可表示为

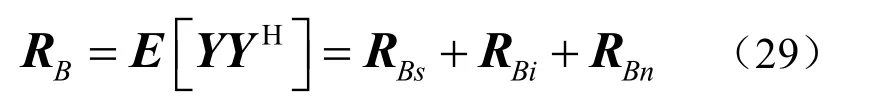
式中，BsR 、BiR 、BnR 分别是波束域信号、干扰与噪声协方差矩阵。于是BNCCB 波束形成器的输出SINR 表达式为

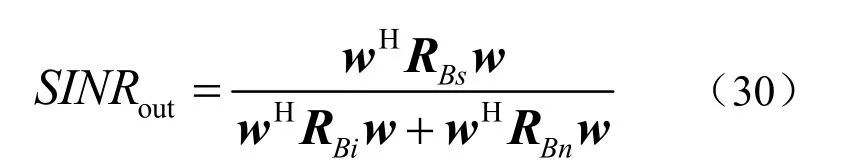
1.4 BRCB 算法

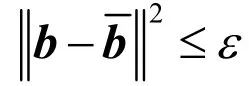
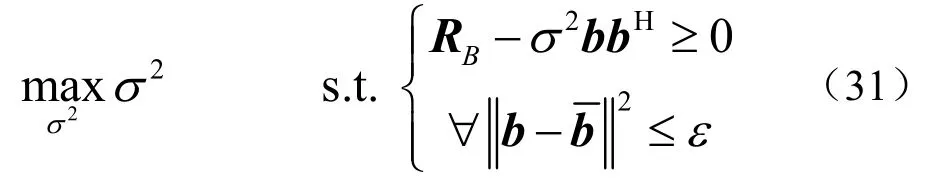
式中，ε 是用户设定的导向矢量误差范数上界。

对于任意给定的b，式（31）中的波束域稳健波束形成问题可以转化为

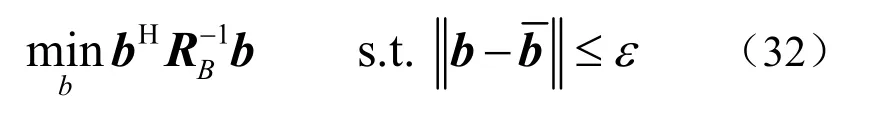
为了避免无用解0=b，假设

式（32）的解显然发生在约束集的边界，因此不等式约束可以写成等式约束：

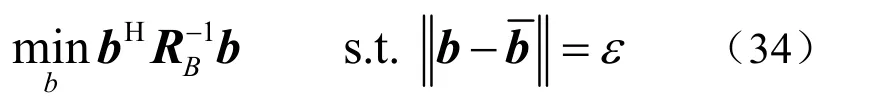
运用Lagrange 乘子法，定义函数

式中，λ ≥ 0是实值Lagrange乘子。上式对 bH求导，并令导数为0，得到

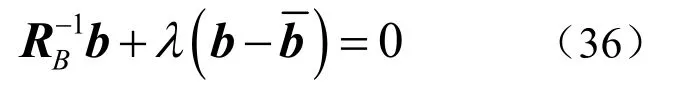
可得上式中b 的解为

由矩阵求逆理论，上式进一步可写成

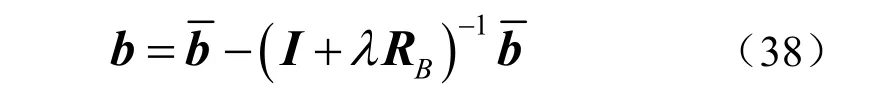
通过特征分解，有

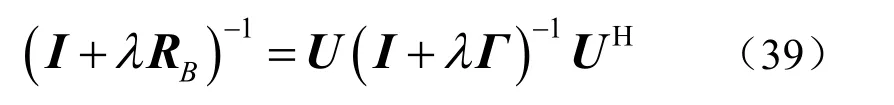
于是，式（38）可以表示为

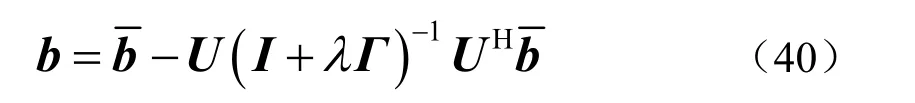
代入下式中，得到估计的信号功率为

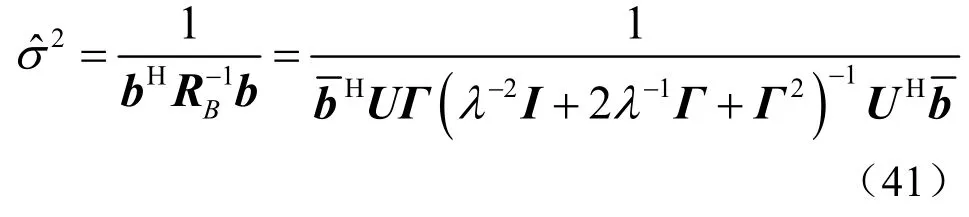
将式（40）代入下式中，得到RCB 波束形成器加权向量为

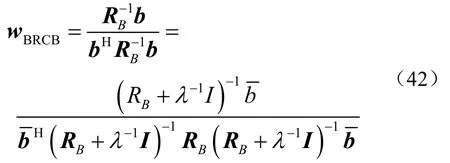
由上式可见，BRCB 方法是对角加载类算法，其对角加载量为1/λ。

将式（40）代入式（34）中的约束函数，可得

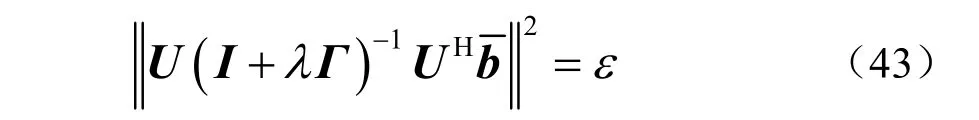
上式可以表示成

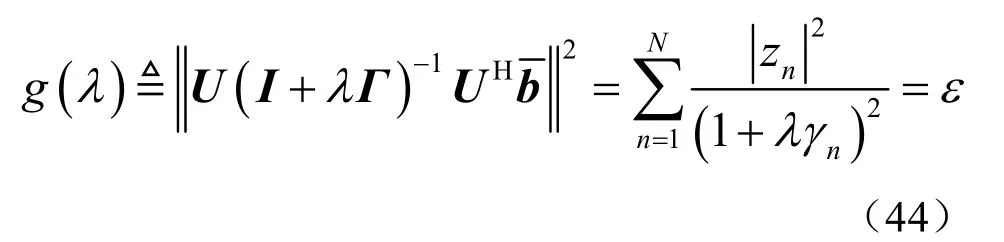
容易看出， g （ λ ）是关于λ 的单调递减函数。由式（33）、（40）与（44）知 g（ 0）＞ ε。由式（44）知limλ→∞g（ λ）= 0＜ ε。因此，式（44）存在唯一解。分别用最大与最小特征值 γ1与 γN代替式中的γn，可以得到λ 的上下界范围

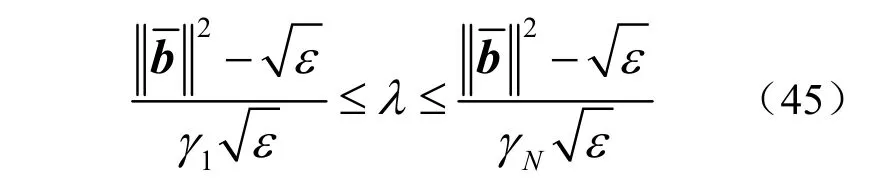
将式（44）分母中的1 去掉，可以得到λ 的另一个上界

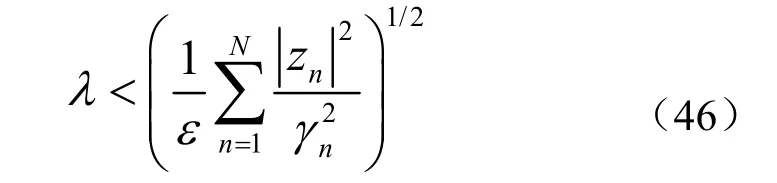
因此，λ 的上下界范围为

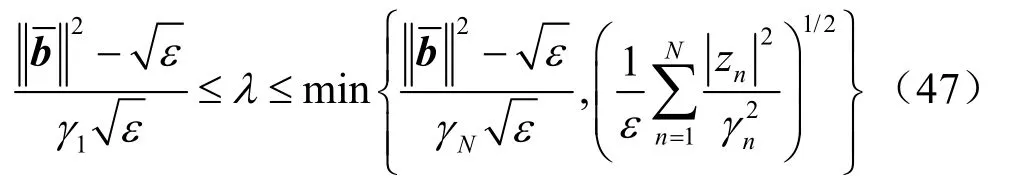
将求解出的λ 代入到式（42）中得到wBRCB。则BRCB 波束形成器在观察视区Θ（θ ∈Θ）扫描的输出功率为

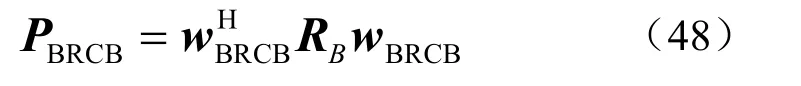
同理，BRCB 波束形成器的输出SINR 表达式与式（30）一致。

2 仿真分析

2.1 算例一

假设空间具有半波长布阵方式的标准线阵，阵元数为16，快拍数为500，两个单频信号分别从θ1=0°、θ2=8°入射进来，SNR1=0 dB，SNR2=10 dB。仿真结果如图3 所示。

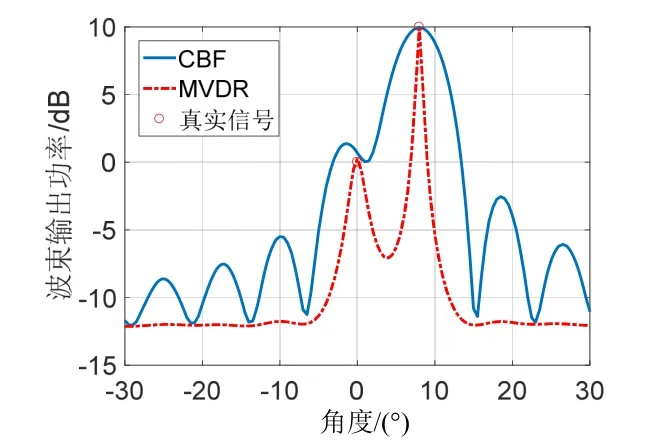
图3 无误差下的CBF 和MVDR 空间谱

结果分析：常规波束形成器的空间谱图中，由于CBF 算法的空间分辨力有限，无法准确分辨出两个信号。而理想MVDR 空间谱中，MVDR 波束扫描得到的空间谱峰值更尖锐，正确显示两个信号。这说明MVDR 波束扫描具有比常规波束扫描更高的方位分辨能力。理想MVDR 空间谱效果很好，但在实际应用中，由于阵列失配问题，MVDR 空间谱性能下降严重。

2.2 算例二

图4 阵列流形误差下的空间谱

结果分析：阵列流形向量误差下，BMVDR 波束形成器空间扫描效果下降严重，已无法分辨出空间中的两个信号。虽然BNCCB 算法能分辨出这两个信号，但估计的信号功率比真实信号功率低。只有BRCB 算法的信号功率估计能力较好，几乎能正确指示信号功率。这表明BRCB 在阵列流形向量误差下具有比BMVDR 和BNCCB 更高的方位分辨力，对阵列流形误差具有一定的稳健性。

用MATLAB R2016b 中CPUTIME 函数分别计算了表1 中6 种算法的运算时间。从表1 可以看出，在本例中，波束域算法计算量通常比阵元域算法小，证明了波束域方法能有效减小计算量。

表1 运算时间比较

2.3 算例三

下面利用仿真分析具体比较BMVDR、BNCCB和BRCB三种算法在不同的阵列失配情况下的性能。

假设空间具有半波长布阵方式的标准线阵，阵元数为16，选择9 个波束，波束扇覆盖范围为[-30°, 30°]。期望信号从θ0=0°处入射，SNR=0 dB，干扰信号从θ=-20°处入射且INR=20 dB。BNCCB 算法中Gwd=1 dB。BRCB 算法中2ε = 。各个仿真均采用蒙特卡洛仿真方法重复试验。图5 为期望信号DOA 估计误差而导致的阵列失配时输出SINR 情况。图中，横坐标表示期望信号DOA 估计值相对于主瓣宽度的误差。

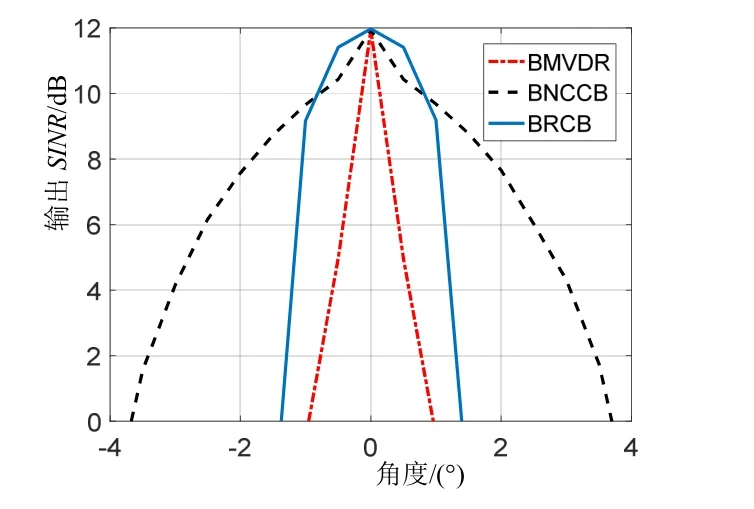
图5 DOA 估计误差下输出SINR

从三个仿真结果可以得到以下结论：

（1）BMVDR 在DOA 估计误差下性能下降严重，BNCCB 和BRCB 在一定误差范围内性能有所改善。当DOA 估计误差较小时，BRCB 对其的稳健性较好；当DOA 估计误差较大时，BNCCB 的稳健性更好。

（2）在阵元位置误差逐渐增大的过程中，BRCB 的输出SINR 比BNCCB、BMVDR 中下降得更缓慢。

（3）阵元域RCB 与MVDR 相比，只需要更少的快拍数就能得到较好的输出SINR。通过波束域处理后，性能再次得到提升。且波束数为7 时的估计性能优于波束数9。

图6 阵元位置误差下输出SINR

图7 有限快拍下输出SINR

仿真结果表明在三种不同的阵列失配误差情况下，BNCCB 在提高DOA 估计误差稳健性方面优于BRCB 和BMVDR，而BRCB 在提高阵元位置误差情况的稳健性方面优于另两种算法，并以BRCB在小块拍情况为例，说明此算法分别从波束域处理和稳健处理两个维度提升MVDR 算法性能。

3 结论

波束域预处理通过一组波束聚焦感兴趣的区域，减小系统复杂度的同时提高其稳健性。本文对BRCB 和BNCCB 算法进行了理论分析及计算机仿真。仿真结果表明，在阵列失配误差情况下，BRCB和BNCCB 较BMVDR 有更好的信号分辨力，且运算量相较于未经波束域处理前有所减小。最后利用仿真实验具体分析了三种算法在不同误差情况下的稳健性能。