船舶典型管路系统低噪声设计研究

柴 凯，楼京俊，朱石坚，丰少伟

（海军工程大学 舰船与海洋学院，武汉430033）

管路系统被称为船舶的“血管”，主要用于输送油、水、气等各类介质，在保障船舶航行、机械设备运转和舰员日常生活等方面发挥着举足轻重的作用[1]。例如管路为主机、辅机、炮管等诸多设备提供燃油、润滑油和冷却水以保证系统正常运行；为空调、饮用水等生活保障系统输送新鲜空气、淡水以保障舰员正常生活；化学灭火、消防损管等安全系统同样布置了大量的管路。但管路系统在实现介质传输功能的同时，也伴随着振动噪声的产生，结构振动和噪声通过管路传至船体结构，成为制约船舶声隐身性能的重要因素。管路系统振动噪声一方面影响管路系统的工作性能，缩短管路元件的寿命，甚至造成管路接头松动，引起流体泄漏和管路破损，严重时造成主、辅机停机而失去动力；另一方面，一些管路元件在一定程度上充当了振动传递的“桥梁”，强烈的振动将会造成主、辅机某些应力集中部位发生破坏[2]。

国内外学者对管路系统振动噪声机理和控制技术开展大量研究工作，取得了丰硕的研究成果。美国海军研制了一种新型智能缓冲隔振装置，可有效降低核潜艇管路系统在作战条件下所受冲击载荷[3]。英国国防局设计了一种主动式管道接头，可有效降低管路连接处的脉冲激励[4]。Ahmadi等开发了一种应用于充液管路的三维吸振器，取得了很好的减振降噪效果[5]。和国外相比，国内管路振动噪声理论研究起步相对较晚，但同样取得飞跃式成果。仪垂杰等从管路系统结构声辐射基本规律出发，讨论了管路结构振动模态的声辐射效率、声场能量分布等与外界激励、系统模态参数之间的关系[6]。闰祥安等利用有限元法建立了潜艇往复泵及其管路系统的理论模型，通过结构振动分析得到管路系统固有频率及振型分布规律，同时提出了一些管路减振降噪措施[7]。尹志勇等对挠性接管、空气消声器、阻尼包覆等管路元件设计标准的适用性及需求进行了分析，采用阻抗-导纳综合法设计了一种船舶管路系统的振动频域响应预测方法[8]。

综合分析国内外研究现状可知，目前研究主要局限于管路系统振动控制元件以及控制方法，从系统整体优化方面对其进行振动控制的研究较少，鲜有关于安装因素对整个管路系统的振动噪声影响的研究。本文以船舶典型管路系统为研究对象，基于传递矩阵法建立典型管路元件的传递矩阵，给出其固有频率和振动响应，设计低噪声优化模型，通过有限元计算和试验验证模型的正确性和有效性。

1 船舶管路系统振动特性分析

1.1 整体结构模型分析

为便于分析管路系统的振动特性，将管路系统简化为如图1所示的闭式结构，其主要部件包括：直管、弯管、弹性支撑、振源（泵、电机等）以及挠性接管等。振源为泵，泵进水和出水管路与压力水筒连接，形成环形回路；管路系统水泵出口处安装有挠性接管，弹性支撑位于水泵出口与压力水筒进口之间的U型工作管段上。泵产生的振动通过挠性接管、直管、弯管等元件沿着水流方向进行传递，同时还通过弹性支撑传递至基座。

1.2 传递矩阵分析

船舶典型管路系统由许多管段、元件和支撑组成，在不考虑各部件运动之间的相互作用时，相关管路元件可独立划分为传递矩阵单元，通常直管等分布质量参数模型的传递矩阵为场传递矩阵，而弹性支撑等集中质量参数模型的传递矩阵为点传递矩阵[9]。直管是管路系统的基本部件，弯管可离散为多段通过拐点连接的直管，形状规则的挠性接管也可简化为直管，因此先分析直管传递矩阵模型，基于直管模型再分析挠性接管和弯管的数学模型。

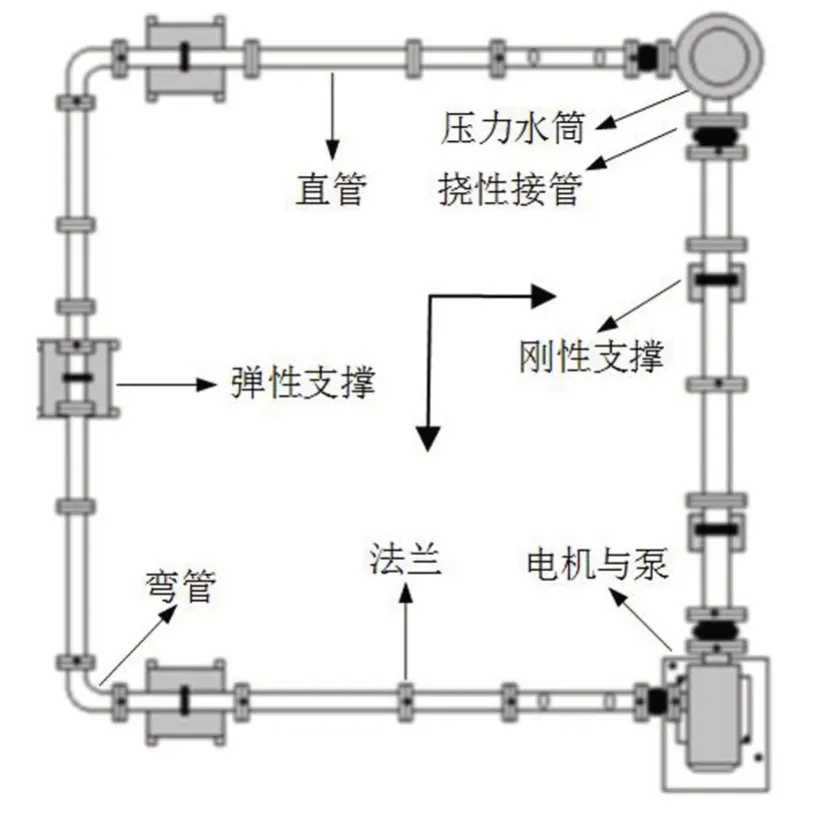
图1 船舶典型管路系统的简化模型

考虑到充液直管的轴对称性，取管道轴线方向为z轴，垂直方向为x轴，水平切线方向为y轴，建立直角坐标系，具体如图2所示。

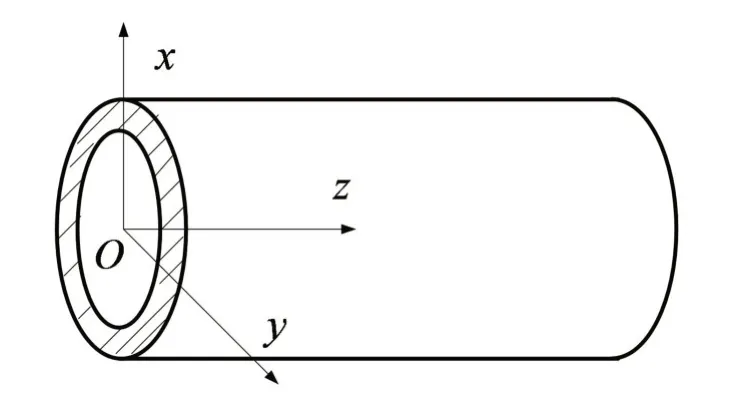
图2 直管的坐标系构建

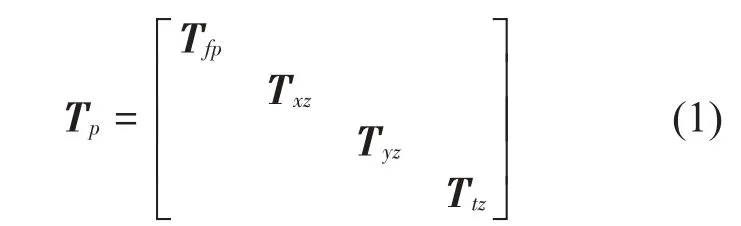
假设充液直管内径为R，壁厚为d，管长为l，正应力为σ，剪应力为τ，管壁内任取一微元体进行受力分析，根据达朗贝尔原理和位移连续条件[10]得到充液直管的振动传递矩阵Tp：其中：Tfp、Txz、Tyz和Ttz分别为轴向、xoz平面和yoz平面、扭转的传递矩阵，其中轴向和两个垂直的横向振动均为4阶，扭转振动为2阶，且四者互不耦合，组合可得直管的14阶总传递矩阵。

法兰、弹性支撑、挠性接管和弯管的简化模型分别如图3所示。

如图3（a）所示，法兰形状较规则，假设法兰内径为d，外径为D，厚度为h，密度为ρP，流体密度为ρf，可依次算出法兰质量Mp，内部流体质量Mf以及绕x、y和z轴的转动惯量Ix、Iy和Iz，同时令充液法兰的总质量M=Mp+Mf。根据达朗贝尔原理和位移连续条件得到法兰的传递矩阵Tf：

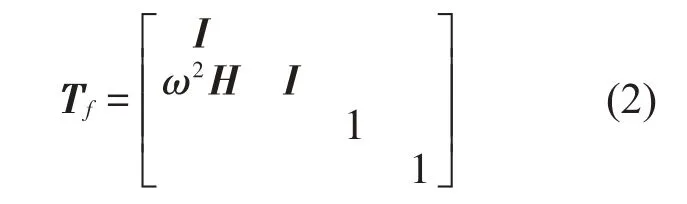
弹性支撑是指支撑点刚度不随频率变化的支撑，它可以用弹簧代替，刚度矩阵为对角阵[12]，将其简化如图3（b）所示。假设弹性支撑在6个自由度的刚度分别为kx、ky、kz，、ktx、kty、ktz；弹性支撑质量为m，弹性支撑绕x、y、z轴的转动惯量为Ix、Iy和Iz，根据支撑反力向量N与位移向量U的关系得到弹性支撑的传递矩阵Ts：

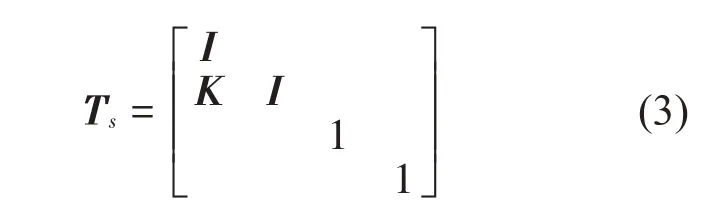
挠性接管主要用作隔振设备的各种进出管路的过渡联接，其结构形式很多，所用的橡胶或者金属材料属性十分复杂[13]。但对于一些形状规则的挠性接管，仍可以将其简化为如图3（c）所示的直管模型。采用直管传递矩阵类似的方法，可得挠性接管横向振动传递矩阵和扭转振动传递矩阵，各传递矩阵之间互不耦合，组合即可得到挠性接管的整体传递矩阵[14]。

对于圆弧形弯管，工程上常按多段斜接的直管离散模型将其离散，具体如图3（d）所示[15]。将弯管的弯曲部分均匀地划分为N段直管单元，各单元之间通过节点连接，假设弯管弯曲半径为R，弯曲角度为Φ，则相邻两个节点拐角，依据达朗贝尔原理和位移连续条件可得：

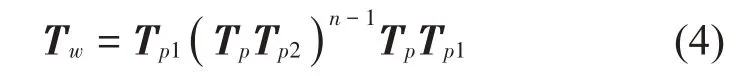
其中：Tp为直管传递矩阵，Tp1为离散后弯管端部节点的点矩阵，Tp2为内部节点的点矩阵。

1.3 振动特性分析

管路系统振动特性边界条件包括流体和结构边界条件。边界条件与管路始末两端的约束有关。本文仅讨论两个典型的边界单元：法兰和通海口。将法兰简化为管端一轴对称质量，流道作为开路或闭路的边界条件；通海口一般固定在船体结构上，其结构边界条件为固定约束条件。

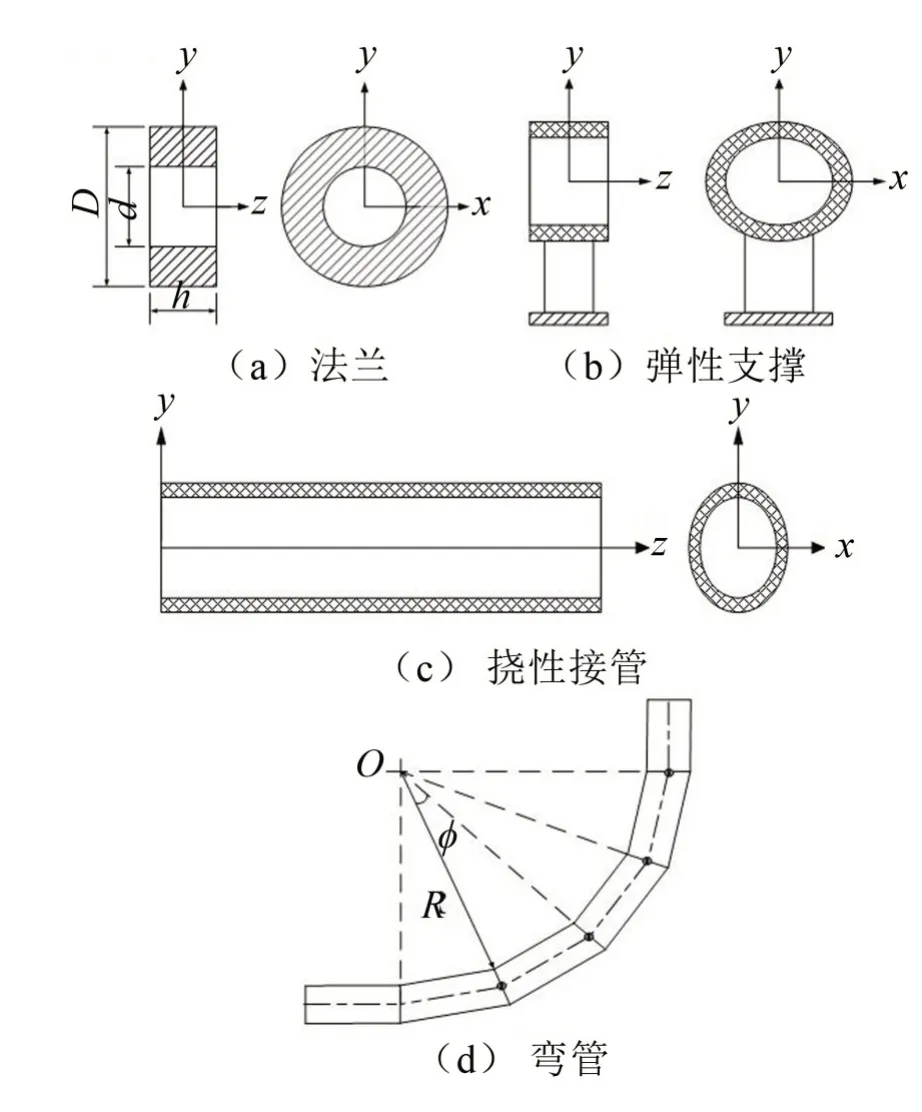
图3 不同管路元件的简化模型

在传递矩阵法中引入边界条件目的是要在始末端得到两个状态向量，使得末端状态向量中的已知个数与始端中未知量个数一致，以便于求解。以一个始末两端边界单元均为开口直管（自由-开口）的管路系统为例。其中已知状态向量用VK1、VKn表示。原来的始末两端状态向量称为未知状态向量，用V1、Vn表示。其始末端两端结构和管内流体的边界条件为：F1=0，P1=0；Fn=0，Pn=0，由此得到始末两端已知状态向量分别为

传递矩阵是频率的函数。对确定的管路系统，当ω=ω0时，其两端状态向量满足传递关系：Vn=T(ω0)V1，同时满足边界条件：V1=VK1，Vn=VKn，那么ω0是管路系统的一个固有频率。通过矩阵变换可以将两端已知状态向量写成已知变量与未知变量的形式（上标K表示已知，U表示未知），则此时传递关系为

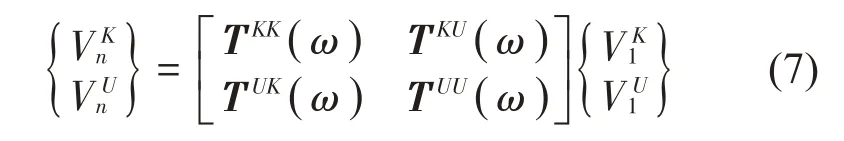
由式(7)可得：

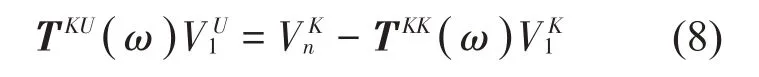
式中：Ve=VnK-TKK(ω)V1K称为系统的激励向量。当

边界条件可以用传递矩阵的形式来表示，并称此传递矩阵为边界点矩阵，用TB表示。“自由-开口”的边界点矩阵为系统自由振动时，有VnK=V1K=0，因此得到：

式(9)即为系统的频率方程。TKU(ω)为系统的频率矩阵。求解此方程即可得到系统的固有频率。

取舰船典型管路系统的U型工作段作为研究对象，建立如图4所示的工作管段的有限元模型，其主要部件包括直管、弯管、弹性支撑、振源（泵、电机等）以及挠性接管，在该管路系统内均匀等间隔地布置4个弹性支撑，并且在泵的出口处安装了挠性接管。为对比分析传递矩阵模型的正确性，利用传递矩阵法以及有限元法分析其振动特性。管路系统的相关结构参数与材料属性如表1所列。

图4 管路系统计算模型

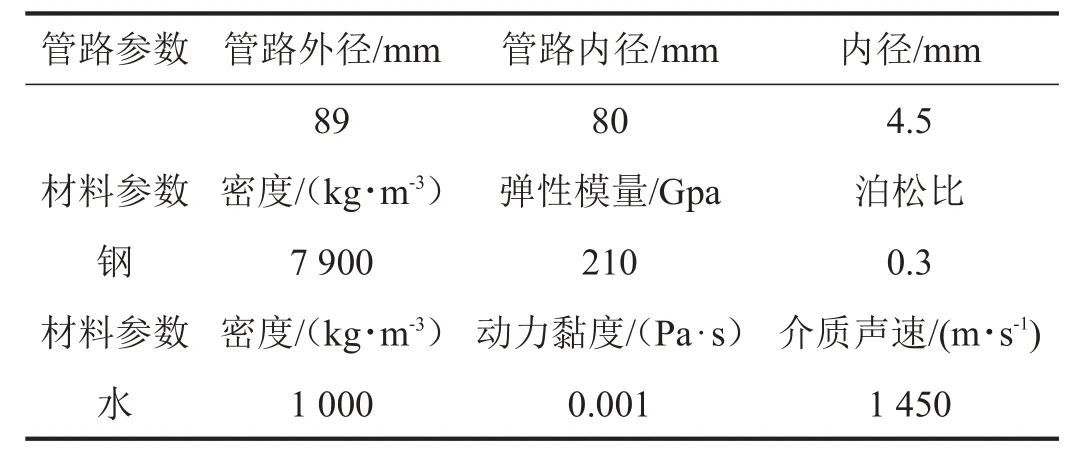
表1 仿真管路材料与结构参数

为验证传递矩阵计算方法的正确性，将传递矩阵理论与有限元仿真两种方法的管路系统固有频率计算结果进行对比，具体如表2所列，由表2可知两种方法吻合程度较好。

表2 管路系统的固有频率/Hz

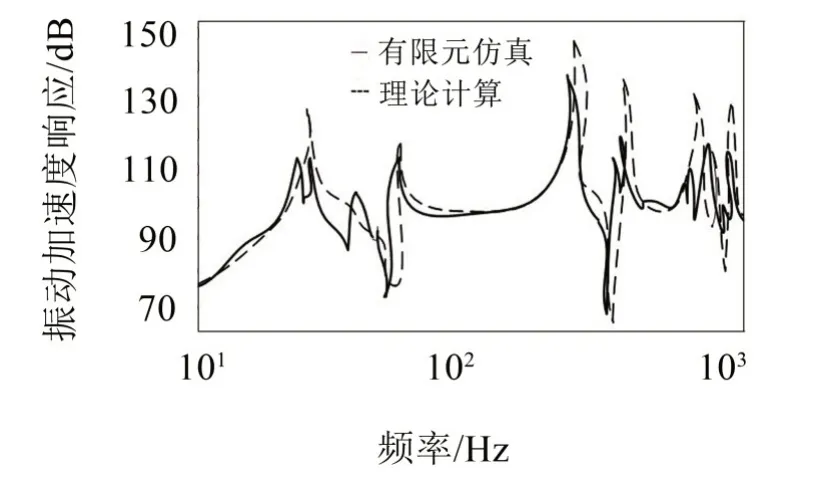
图5 管路系统振动响应对比图

此外，为进一步验证传递矩阵方法的准确性，在管路系统计算模型中的进口端施加一沿垂直方向的单位激励力，并得到了管路末端指定点垂直方向上的振动响应。如图5所示为系统指定点的振动响应对比频谱图。由图可知，计算结果与有限元仿真结果比较吻合，证明了传递矩阵计算方法和程序的正确性。同时，管路系统由于泵的复杂振动、元件及介质的耦合作用，存在多物理场、多尺度及流固耦合非线性等特性，振动特性非常复杂。管路系统的非线性不仅体现在流体流动方程是非线性的，而且耦合运动的特性将随着结构振动的幅值不同而变化。而非线性系统普遍存在多值性，相应的幅频特性曲线的骨架线不是直线，可能朝频率增大方向或较小方向弯曲，从而使整个曲线族朝一侧倾斜，产生单个频率对应多个振动加速度的情况。

2 有限元仿真分析

2.1 有限元建模

整个管路系统中直管是最基本的构件，在ABAQUS有限元软件中建立直管模型，其结构参数和材料参数与表1所列相同。

弯管在有限元软件中的建模过程较为复杂，可通过扫掠方式实现。弯管管段实际长度为250 mm，弯曲半径为0.5 m，管道外径为89 mm的弯管的弯曲角度α为90°。

考虑到弹性支撑对称性将其简化为弹簧结构，卡箍装置可简化为刚性套圈紧固在管道，卡箍内环以coupling 接触形式连接两相互垂直弹簧，形成弹性支撑简化模型。

在管路系统进口处安插附有橡胶属性的挠性接管，形式采用双球体，其长度为135 mm，横向拉伸为10 mm，轴向拉伸为6 mm，轴向压缩为12 mm，偏转角度为15°。管路元件见图6。

根据管路元件的建模方法，建立如图7所示的管路系统低噪声设计模型，具体包含直管、弯管、弹性支撑、挠性接管和阀门等构件。右端管口为管路系统的进口，依次经过直管、阀门、双球体挠性接管、弯管、弹性支撑，通向左边末端的出口。右边末端是电机激励，进口处安装阀门（黄色区域），挠性接管安装在振源附近，达到减振降噪的目的。在模型左端管路进口处的指定激励点上，作用单位激励力以模拟电机所产生的频率为50 Hz激励。弹簧一端处于固支状态，一端和管路指定连接点连接，整个模拟管路系统除所使用弹性支撑被基座固定外，其余部分均处于自由状态。

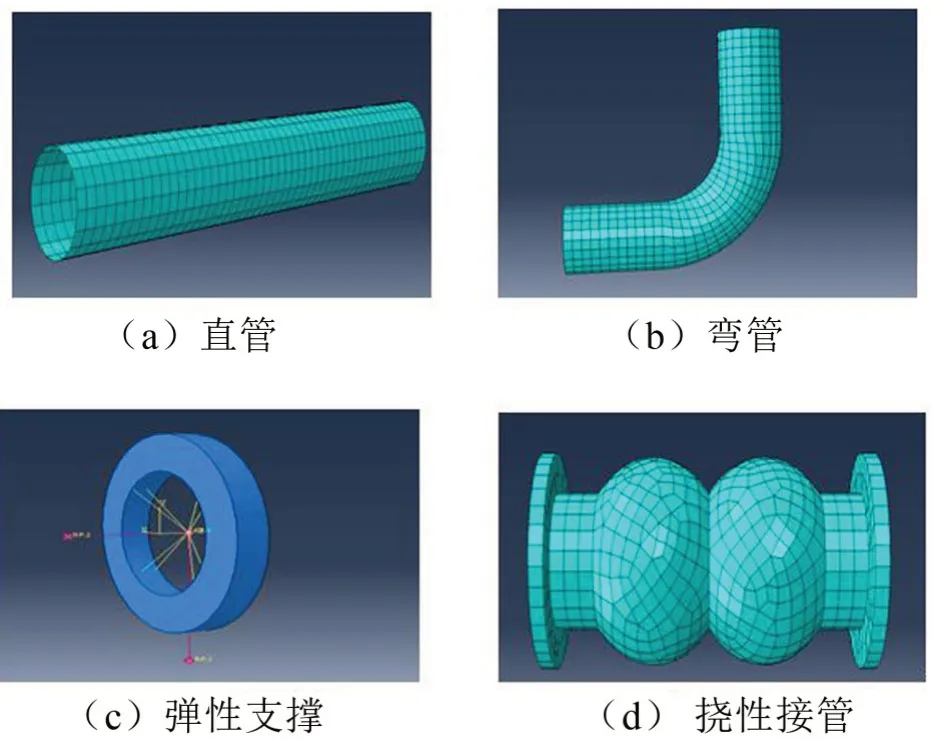
图6 管路元件有限元模型

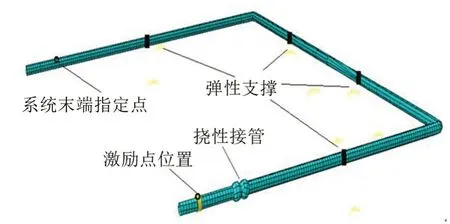
图7 典型管路系统有限元模型

2.2 有限元结果分析

为验证管路系统模型中挠性接管的隔振效果，选取挠性接管进出口两点进行振动响应对比分析，由图8可知，挠性接管具有良好的隔振效果。

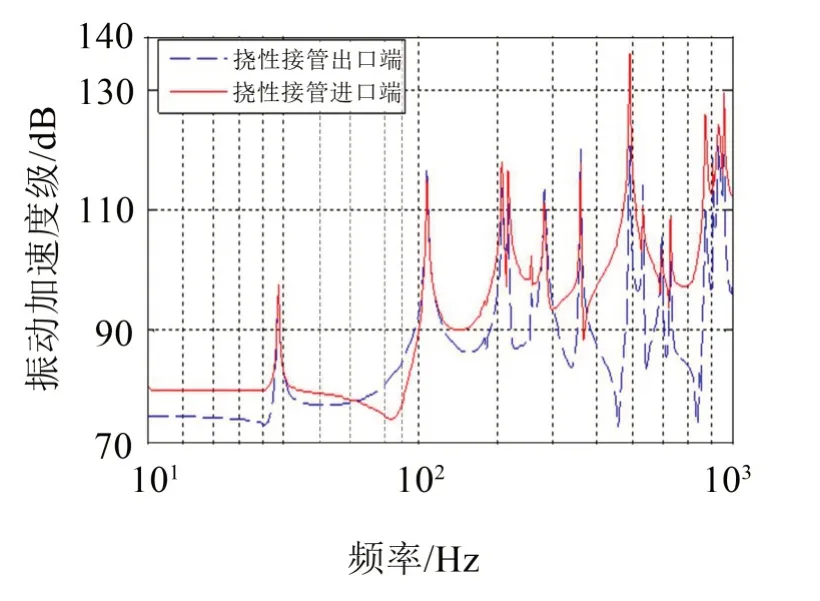
图8 挠性接管进出口处振动响应频谱图

为分析弯管振动的传递规律，选取弯管前后两端位置点的振动响应进行对比分析。由图9可知，弯管前后的振动加速度级变化不明显，在100 Hz附近弯管后端的振动响应有所增大，而在其它频段内弯管前后两端的振动响应几乎一致，单根弯管对管路系统振动传递特性并没有太大的影响。

图9 弯管前后端振动响应频谱图

3 试验分析

3.1 实验台架设计

试验台架如图10所示，主要由电机、泵、直管、弯管、挠性接管、弹性支撑和测试系统等组成，它不仅能较真实地模拟船舶典型管路系统的动态特性，而且可以较好地验证管路系统低噪声设计方法。试验台架所用管路材料以及结构参数如表3所列。

图10 管路系统测试试验台架

典型船舶低噪声设计管路系统基本构成：

（1）电机、泵：CLG型卧式离心泵出口压力为0.32 MPa，电机功率为15 kW，额定转速为3 000r/min，频率为50 Hz；

表3 试验管路材料与结构参数

（2）挠性接管：实验台架中所用的DN80型双球体橡胶挠性接管通过法兰连接在管路系统中，其长度为135 mm，横向拉伸为10 mm，轴向拉伸为6 mm，轴向压缩为12 mm，偏转角度为15°；

（3）弹性支撑：规格为DN80，用于外径为90 mm的管道，弹性支撑内附规格为BE-60型隔振器，其x向额定载荷为22 kg，z、y方向的额定载荷为44 kg。

3.2 试验方法

试验主要任务是测试在电机以及稳定流体激励作用下管路系统各测点振动加速度响应，验证低噪声设计模型的正确性。在安装好各个测点的传感器之后，将电机通电运行并带动卧式安装的水泵一起运转，待系统在电机以及管内流体激励的作用下形成稳定工况后，再进行数据采集。

试验以数据采集仪所采集的挠性接管进出口三向加速度测点A1 和A2、弯管前后单向传感器测点1#和2#的振动加速度响应作为实验分析的表征参数，分析管路系统在不同试验方案下在10 Hz～1 000 Hz频段内的振动加速度级（dB）。测点位置如图11所示。

在整个试验过程中，水泵转速保持2 900 r/min不变，管内流量为100 t/h。当电机和水泵工作时，工作流体从压力水筒流出，经过两个刚性支撑架支撑的直管进入试验工作段（U型管段），经过循环之后，最后又回流至压力水筒。

图11 测点布置位置示意图

3.3 试验结果分析

为验证总体试验方案所用挠性接管隔振效果，在工作段挠性接管的进出口处安装有三向加速度传感器，测量挠性接管在电机与泵满载工作的状态下X、Y以及Z向的振动响应，采集测点A1 和A2的数据，分析其振动传递特性。

由图12可知，在频率约在100 Hz和500 Hz附近时，出现了出口处振动加速度级高于进口处或振动加速度级下降不明显的现象，即挠性接管在此处存在一个共振点，此时振幅最大。因此，以100 Hz 和500 Hz作为频率分界点进行分析，挠性接管在10 Hz～100 Hz频段范围隔振效果较差，在500 Hz～1 000 Hz频段范围其隔振效果十分显著，其中挠性接管在Y轴方向上的隔振效果最好，进出口前后振级相差25 dB，X轴、Z轴方向次之。由此可知挠性接管在低频段的隔振效果较差，甚至出现振动加剧，而在500 Hz～1 000 Hz频段内，隔振效果比较明显。

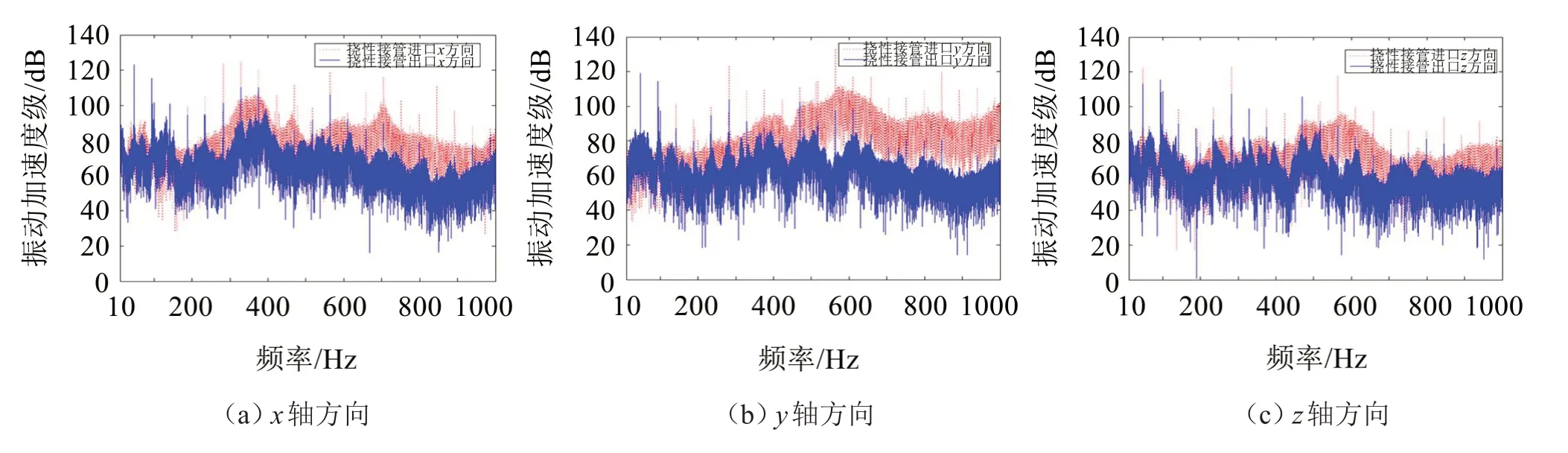
图12 挠性接管进出口处的振动响应对比

在试验管路系统中设置一段弯管，通过试验探究了挠性接管安装在弯管前端和弯管后端对管路系统的振动传递的影响，如图13所示。挠性接管的两个安装位置分别为位置1和位置2，以其出口处的振动加速度级为表征参数，采集两种不同位置工况下挠性接管出口处测点A2的振动信号，对其所受到的安装位置影响开展研究。

图13 不同位置挠性接管安装示意图

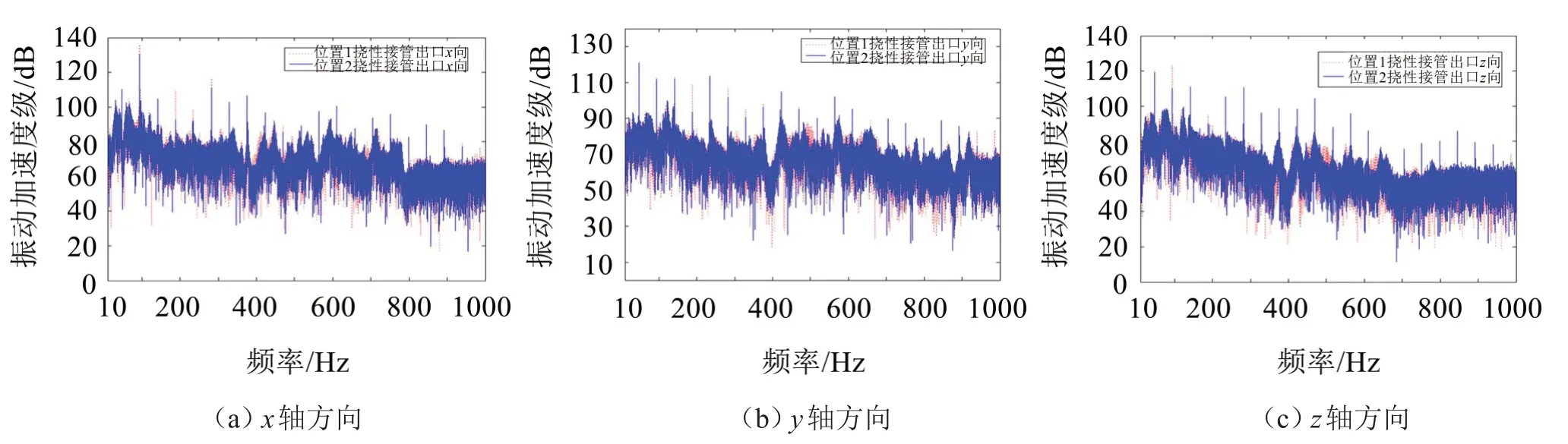
图14 挠性接管不同安装位置工况下的振动响应对比

由图14可知，挠性接管在10 Hz～1 000 Hz频段内X、Y、Z三向的振动加速度级相差很小。根据不同位置挠性接管出口处的振动传递特性发现，两种工况下相同测点的振动加速度级相差很小，说明无论是挠性接管与水泵出口直接相连（即安装在弯管前端）或是连接在水泵出口的弯管后端，其对管路系统的振动传递影响较小。这对实船的挠性接管的安装位置以及维修保养有着重要意义，挠性接管安装在管路系统不同位置比较实验结果表明：挠性接管的布置应尽量靠近振动源，若船上实际安装空间不允许，可根据空间位置适当调整挠性接管与振动源的相对位置，调整的位置应尽量靠近振动源。

由图15可知，挠性接管安装在弯管前段，低频振动相对较强，但峰值差别并不大；而对于1 000 Hz的高频振动降低较为明显。

图15 挠性接管安装位置不同时x轴方向振动响应频谱对比

采集弯管前后测点1#和2#数据，分析其振动传递特性。由图16可知，弯管前后的振动加速度级并没有大落差，由此可以推知单个弯管对管路系统的振动传递影响较小，但这并不能推断出布置一定数量的弯管对管路系统的振动特性的影响不大，管路系统的振动特性可能会随弯管数量的增多而发生较大的改变，从而不利于系统的减振降噪。在实际工程应用中应考虑适当地减少系统中的弯管数量。

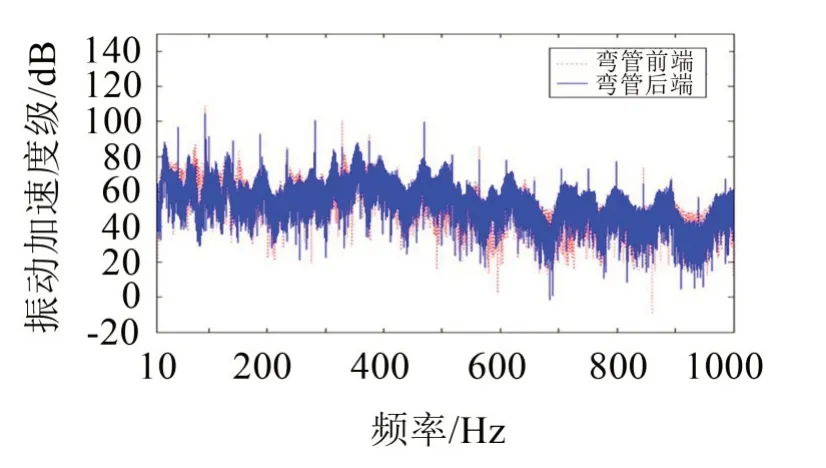
图16 弯管前后振动响应对比

4 结语

本文以船舶典型管路系统为研究对象，提出了一种综合考虑管路系统结构参数、流体性能和实船安装因素的低噪声设计方法。利用传递矩阵法计算管路系统固有频率等振动特性并对比验证了传递矩阵理论的正确性，利用仿真以及试验手段验证了低噪声设计模型的有效性。主要工作和结论总结如下：

（1）用传递矩阵理论建立了船舶典型管路系统低噪声设计模型。该传递矩阵模型能有效地对管路系统相关元件模型进行理论计算，可以准确地分析管路系统振动特性。

（2）建立了管路系统ABAQUS有限元模型。该模型能够准确地模拟管路系统的振动传递特性，利用有限元软件强大的后处理功能对模型进行了振动特性分析，仿真结果符合工程实际规律。

（3）船舶典型管路系统试验测点布置合理，工况稳定，试验结果验证了理论分析和有限元仿真计算的正确性。利用试验结果分析了挠性接管的安装位置影响、弯管前后的振动传递规律，并针对挠性接管以及弯管提出了几点低噪声安装建议。