安徽省人均GDP 与城镇化率相关回归分析

程中林，朱海婷，朱家明

1.安徽外国语学院公共基础课教学部，安徽 合肥231201;

2.安徽建筑大学数理学院，安徽 合肥230601;

3.安徽财经大学统计与应用数学学院，安徽 蚌埠233030

城镇化建设与经济发展的关系很早就受到经济学家的关注.国外学者Berry 采用主成分分析方式［1］、Renaud 使用面板数据分析法［2］都证明经济发展与城镇化进程存在一定的相关性.Vernon Henderson 通过构建模型进一步证明城镇化率与人均GDP 之间的相关系数［3］.国内学者周一星对157 个国家和地区的数据进行分析后证实，大部分国家或地区的城镇化率与人均GDP 序列之间均呈现对数曲线关系［4］.赵民和张颖通过模型拟合，进一步证实了城镇化建设水平与经济发展状况存在某种相关系［5］.

随着城镇化的逐步推进，人口、土地及资本等各种资源聚集在城市，从而产生经济规模化效应，有利于居民收入大幅增加，实现经济快速发展.同时，城镇化也是一把双刃剑.城镇化是由传统向现代进程发展的必经之路，它可以快速带来二线、三线城市的发展，为城市居民提供了大量的就业机会.然而，在推动城镇化建设的过程中，往往会忽视乡村的发展、资源的保护和社会文明的发展等等［6］.近五年安徽省城镇人口数量增加约550 万人，常住人口城镇化率达到50.5 %，初步进入城市主导型社会，城镇化与社会经济发展是相互推进的，因此本文就安徽省城镇化建设与经济发展的客观情况，对二者的相互影响程度进行研究.

1 安徽省城镇化率与省人均GDP

1.1 探索性分析

1.1.1 数据来源

本文研究分析中所依托的数据为:2003 年～2017 年安徽省16 个市城镇化率与人均GDP 的数据，均来自安徽省统计局2003 年～2018 年统计年鉴.

1.1.2 描述性统计

首先对收集的数据进行描述统计，详见表1.

表1 2003 年～2017 年省城镇化率与省人均GDP 描述统计表Tab.1 Statistical table describing urbanization rate and per capita GDP in 2003 ～2017

根据表1 结果，城镇化率的最小值为32.00 %，最大值为53.49 %;标准偏差为6.82.人均GDP 最小值为6 375.40，于2017 年达最大值43 401.36，标准偏差为12 588.10.不难看出，15 年间人均GDP 的增速明显高于城镇化率.

2003 年～2017 年省城镇化率呈稳步增长的趋势，但增长幅度不大.省人均GDP 在2003 年～2017 年也逐年增加，但其增长幅度逐年不一.

1.1.3 研究序列变化的趋势特征

就城镇化率与人均GDP 增长特征，分别计算增长速度

运用Excel 描绘城镇化率增速与人均GDP 增速折线图如图1 所示.

1.1.4 研究人均GDP 与城镇化率相关关系

SPSS 是运用大量市场调查统计的数据进行分析，从而得到科学结论的工具.因其易用性和功能强大已成为目前最流行的数据统计工具之一. 它是国内进行归类决策、市场分析、社会学、医学统计和金融学等专业统计分析应用最广的软件.

将2003 年～2017 年省人均GDP 与省城镇化率数据导入SPSS 进行相关分析(表2)，两变量相关系数为0.926，相关程度很高，P 值= 0.000，两变量显著相关.

图1 2003 年～2017 年安徽省城镇化率与人均GDP 增速Fig.1 Urbanization rate and per capita GDP growth in Anhui province from 2003 to 2017

表2 人均GDP 与城镇化率相关性检验表Tab.2 Test table of correlation between GDP per capita and urbanization rate

1.2 省城镇化率与人均GDP 曲线拟合

根据人均GDP 与省城镇化率的趋势线变化，初步采用拟合二次多项式模型和指数模型.

1.2.1 二次多项式回归

将2003 年～2017 年安徽省城镇化率与人均GDP 数据，利用SPSS 回归二次多项式，得到一元二次回归方程为

可决系数:R2= 0.989 8.

1.2.2 指数模型回归

将2003 年～2017 年安徽省城镇化率(t)与人均GDP 数据，利用SPSS 回归指数模型.变量系数b1=0.082，b0= 544.089，拟合指数模型为

可决系数:R2= 0.972 0.

1.3 模型优化

对2003 年～2017 年省人均GDP 与城镇化率数据回归的二次多项式与指数模型曲线，实测数据均匀散布在拟合曲线两侧.拟合的指数模型为

将指数模型转换为线性模型即为

可决系数:R2= 0.9720.

1.3.1 模型检验

对拟合的二次多项式模型进行模型显著性检验，二次曲线回归模型t 统计量为-11.030，P 值= 0.000，模型显著有效.

对拟合的指数回归模型进行模型显著性检验，指数回归模型t 统计量为-11.030，P 值=0.000，模型显著有效. 对拟合的指数回归模型进行模型显著性检验，指数回归模型统计量为-11.030，P 值= 0.000，模型显著有效［7］.

观察表3、表4，所有变量的系数都通过显著性检验，因此两个拟合模型均满足显著性.

1.3.2 模型误差

对比两模型好坏，将两模型误差分别计算.

表3 二次曲线回归模型系数表Tab.3 Table of coefficients of quadratic regression model

表4 指数回归模型系数表Tab.4 Coefficient table of exponential regression model

由表5 知，二次拟合模型误差均小于指数模型误差，所以二次多项式拟合效果较精确.

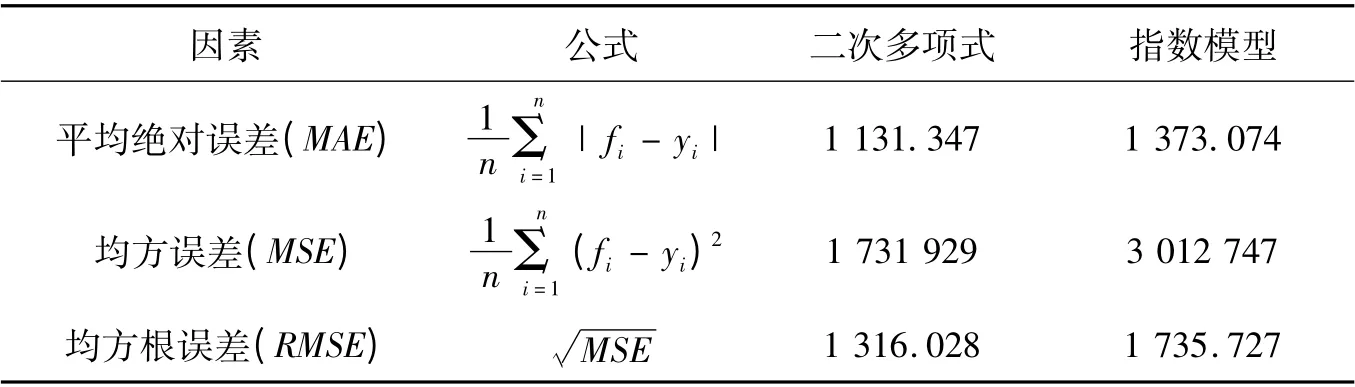
表5 二次曲线回归模型与指数模型误差指标对比Tab.5 Comparison of error index between quadratic regression model and exponential model

1.3.3 误差修正模型

首先判断变量间协整关系后，可以描述长期均衡关系，但不能表述变量短期偏离趋势.建立误差修正模型采用的是E-G 两步法.引用Grange 表述定理［8］:如果变量X 和Y 是协整的，假设两变量X 和Y 的长期均衡关系为

则它们间的短期非均衡关系总能由一个误差修正模型表述

其中

其中λ 是短期调整参数，由长期均衡关系产生误差修正项，后将误差修正项当作一个变量，再建立最小二乘回归模型.

(1)协整关系检验.协整检验也就是非平稳序列的因果关系检验，是为排除非平稳序列可能出现的伪回归情况.首先引入单整的概念，如果一个非平稳序列经过k 次差分后，可以转变成平稳序列，我们就称该序列是k 阶单整时间序列.如果两个序列均是k 阶单整，且其线性组合(如ax +by)是(d -b)阶单整，其中d ＞b ＞0，则称两序列是(d，b)阶协整.协整关系表示两序列长期稳定的均衡关系［9］.

此处仅讨论拟合的指数模型转化成的线性模型，记pcg 为人均GDP 变量，ur 为城镇化率变量. 检验ln(pcg)与ur 具有协整关系.运用Eviews 单位根检验，判断序列pcg1 = ln(pcg)为三阶单整，序列ur 为三阶单整，此时满足人均GDP 的对数序列与城镇化率是同阶单整.令a = 10，b = 10，此时a·ln(pcg)+ b·ur 为1 阶单整.

表6 人均GDP 标准化对数序列与城镇化率标准化序列的ADF 检验Tab.6 ADF test of standardized logarithmic sequence of per capita GDP and standardized sequence of urbanization rate

表7 人均GDP 标准化对数序列与城镇化率序列线性组合的ADF 检验Tab.7 ADF test for linear combination of standardized logarithmic sequence and urbanization rate sequence of GDP per capita

对残差序列进行ADF 检验，检验结果见表8.

表8 模型残差序列单位根检验Tab.8 Model residual sequence unit root test

从表8 不难看出，在5 % 显著水平下，均拒绝了原假设，因此各变量之间存在协整关系.

(2)误差修正模型.建立误差修正模型描述城镇化率和经济增长的短期变动关系［9］.对于偏离长期趋势的短期波动，构建ln(pcg)、ur 与误差修正项ecm 的模型如下:

R2= 0.986 697，如上得到结果，模型拟合程度有很大改善，模型拟合效果较好. 误差修正项系数为0.841 636，说明出现短期变化后会以0.841 636的强度回到长期趋势状态.

(3)结论.以上检验人均GDP 与城镇化率具有协整关系，认为两变量的回归方程有效，且在原指数模型的基础上进行误差修正，使得其模型更加优化.

2 安徽省内各市城镇化水平与市人均GDP

2.1 探索性分析

2.1.1 聚类分析

上文据2003 年～2017 年省城镇化率与人均GDP 数据，研究了省城镇化率与人均GDP 的相关性和拟合回归模型.现据2010 年～2017 年安徽省16 个市城镇化率与人均GDP 数据，研究安徽省内各市发展水平，研究方法是对16 个市进行聚类分析［10～12］.将16 个市划分三个类，将三类从左往右分别记为一、二、三类，得聚类图如图2 所示.

2.1.2 聚类分析检验

根据三个类别数据，研究三个类别是否满足组间具有显著差异，并对所有市发展水平进行分类排行.首先计算各类城镇化率平均值.

对三类城市每两类进行t 检验，见上表10、表11.分析两组t 检验结果，一类与二类的t 统计量对应的P 值为5.837e-05，说明一类与二类具有显著差异;二类与三类的t 统计量对应的P 值为4.23e-11，说明二类与三类也具有显著差异.因此可以认为一类、二类、三类之间具有显著差异. 三类的方差分别为11.688 5、13.030 21、2.976 132，表明三类城市组内差异性均较小.

图2 安徽省16 个市据2017 年市城镇化率的聚类图Fig.2 The clustering chart of Anhui province according to the urbanization rate of 16 cities in 2017

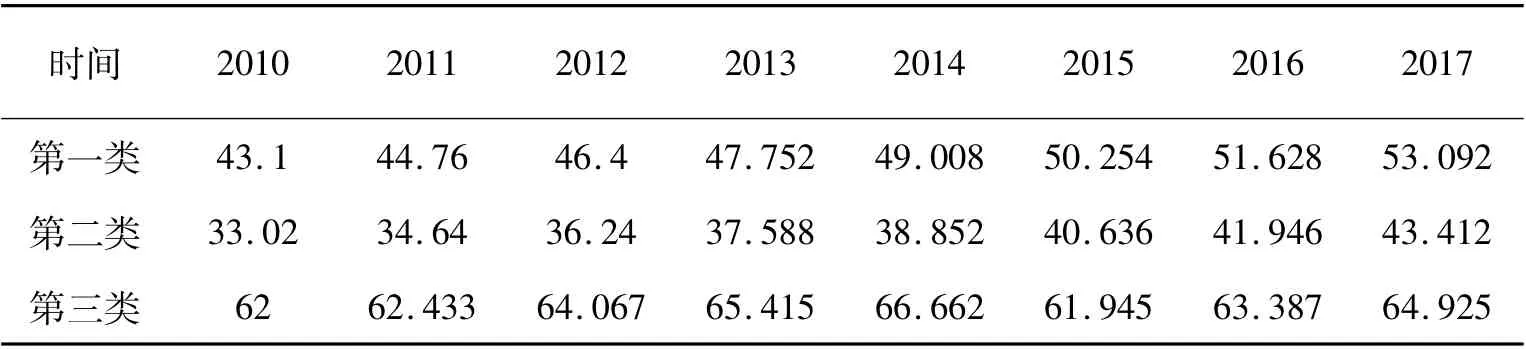
表9 三类城市城镇化率平均值Tab.9 The average urbanization rate of the three types of cities

表10 第一类与第二类城市t 检验表Tab.10 City t test table of Category 1 and category 2

表11 第二类与第三类城市t 检验表Tab.11 City t test table of Category 2 and category 3

2.2 安徽省各市城镇化综合指标测算

2.2.1 城镇化评估指标体系的构建

指标选取依据城镇化发展目标，体现城镇生活质量水平、城镇化水平、就业以及教育服务水平［13］.主要包括如下几个项目:城镇化水平、城市基础设施建设情况、人民就业及收入情况、城市义务教育水平.具体指标为城镇化率、城市建设用地、公共设施用地、城市人口密度、人均城市道路面积、人均公园绿地面积、公交车客运总量、非私营单位就业人数、财产净收入、转移净收入、农村人均可支配收入、中学毕业生人数、小学学校数、高等教育毕业生数［14］.

2.2.2 因子分析

以上衡量城镇化指标共14 个，包含信息内容繁杂，其中城镇化率为必要信息.下面考虑对反映安徽省城镇化的剩余13 个指标进行因子分析，筛选重要指标，利用2017 年省总计及16 个城市的指标数据，利用R 软件采用最大似然法进行因子分析，分析结果如表12.

表12 是因子载荷矩阵表，由该矩阵表反映前两个因子对于各变量的载荷系数［15］.其中因子1 在变量X1、X2、X6、X7、X10～X13上系数较大.这几个变量主要描述城市建设基础、公交客运总量、非私营单位就业人数及教育等数据，相对于财产净收入、人均公园绿地面积等，该因子并没有很大体现，可以将第一因子视为城镇化成果因素.第二因子则在X4、X8、X9上载荷较大，可以将该因子视为城镇化发展因素，将此两个指标作为衡量标准［16］.因子表达式分别是

表12 城镇化指标两个主因子载荷Tab.12 Two main factors in the urbanization indicators load

得到因子载荷矩阵，再依据16 个市具体指标数值，使用回归方法计算因子得分如表13，然后根据因子得分对16 个市进行分类.

表13 省内各市综合得分矩阵表Tab.13 Comprehensive score matrix of each city

依据因子得分矩阵表，对16 个市进行再分类，以Factor 1 值较小和Factor 2 值较高两个标准，将16 个市分为三类，分类结果为:由Factor 2 得分最小的5 个城市:六安、安庆、宿州、亳州、阜阳;对于剩余11 个城市，综合Factor 1、Factor 2 均较大的六个城市:淮南、铜陵、淮北、马鞍山、芜湖、合肥;Factor 2 得分不高且Factor 1 得分较低的五个城市为:蚌埠、滁州、宣城、黄山、池州.这个分组与图3 中聚类结果相同，与城镇化率也有相同变动程度.认为Factor 1 得分与Factor 2 得分均满足数值越高，城市发展水平越好.

图3 城镇化评估指标体系Fig.3 The evaluation index system of urbanization

根据对因子的解释，Factor 2 是反映城镇化成果的因素，很大程度上反映这个城市发展的成效，无论是设施、交通、就业还是教育都极大地反映了城镇化对社会发展的益处以及这个城市已发展成效在城镇化上的体现［17］.Factor 1 是城镇化发展因素，这个因子得分反映了这个城市可发展潜力，认为数值越小，该城市未完全得到发展的程度越高;数值越大，认为该城市受到城镇化普及的程度越高. 因此结合Factor 2、Factor 1，两得分均较高的六个城市淮南、铜陵、淮北、马鞍山、芜湖、合肥为安徽省发展水平较好的六个城市;而Factor 2 得分较低的5 个城市六安、安庆、宿州、亳州、阜阳，已经有城镇化普及但还未有很好的发展.

2.3 各市人均GDP 与城镇化指标主因子回归

2.3.1 线性回归

线性回归分析是通过变量之间的数学表达方式来定量描述变量间相互关系的数学过程.通过利用数学表达方式，根据自变量的取值来预测因变量的取值.如果是多个因素作为自变量，还可以通过因素分析找出那些自变量对因变量的影响是显著的，哪些是不显著的.多元线性回归模型是含有多个解释变量的线性回归模型，应用于解释被解释变量与其他多个变量直角的线性关系［18］.其数学模型为

公式(11)表示一个p 元线性回归模型，由p 个解释变量X 的变化引起的线性变化，其中ε 是随机误差，β0，β1，...，βp为模型中的未知参数.

上文中以两个因子用于对16 个城市进行分类，现研究各市人均GDP 与13 个城镇化指标的关系，建立线性回归模型.

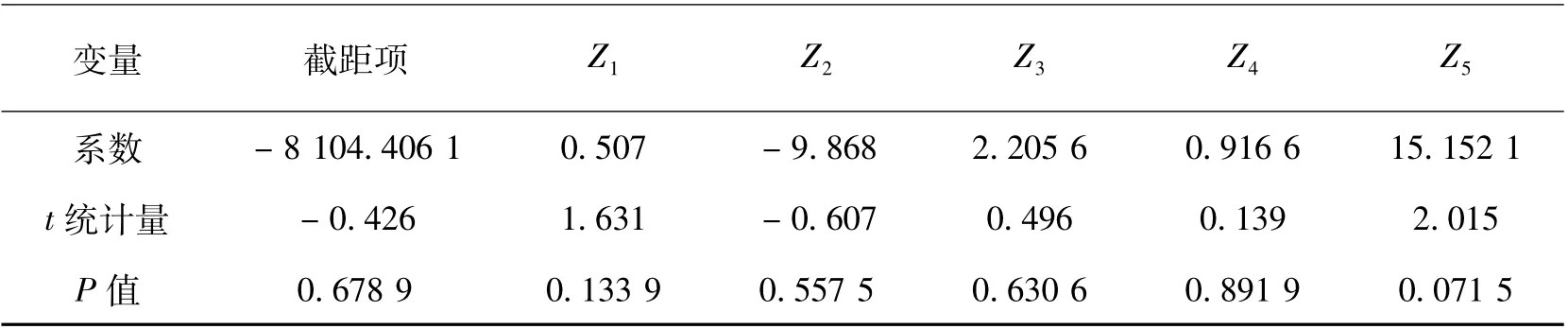
表14 主因子回归结果Tab.14 Principal factor regression results

整理人均GDP 与城镇化因子的方程为

R2= 0.870 4，F = 13.43，P 值= 0.000 36.其中y 表示人均GDP.可以看出方程显著成立，模型拟合效果良好，但参数均不通过显著性检验.

2.3.2 逐步回归

逐步回归的基本思想是将变量逐个引入模型，每引入一个解释变量后都要进行F 检验，并对已经选人的解释变量逐个进行t 检验.当原来引入的解释变量是由后面解释变量的引入变得不再显著时，则将其删除.从而保证每次引入新的变量之前回归方程中只包含显著性变量.这是一个反复的过程，直到既没有显著的解释变量选人回归方程，也没有不显著的解释变量从回归方程中剔除为止，从而保证最后所得到的解释变量集是最优的.

下由人均GDP、城镇化率和5 个因子得分进行逐步回归，在尽量不降低模型拟合效果的前提下，筛选出较少的指标，最终选择模型为

R2= 0.867 6，F = 18.02，P 值= 8.538e -05，此时参数均通过显著性检验，且方程拟合效果良好.

据如上人均GDP 与城镇化主要因子的方程，得到人均GDP 与各变量的方程［19］.

该方程为人均GDP 与城镇化率的线性回归方程，另外X1～X13是描述城镇化率的若干变量，每个变量也有其回归系数，回归系数为正，说明其对人均GDP 有正向促进作用，数值大小反映其对人均GDP 的影响程度.

3 研究结论及建议

3.1 省城镇化与省人均GDP 模型构建

采集2003 到2017 年安徽省城镇化率与人均GDP 数据，利用SPSS 软件，构建二次曲线及指数回归模型，并对两个模型进行检验，二次曲线模型与指数模型拟合效果均较好，均达到0.95 以上，但指数模型较二次曲线模型误差较大，因此选择二次曲线模型较优.接着研究人均GDP 与城镇化率具有协整关系，若两变量不存在协整关系，模型可能会出现伪回归现象.最后对残差进行检验，建立误差修正模型，使得模型更具说服力，解释了短期波动.

3.2 市人均GDP 与市城镇化各指标模型构建

第一步利用R 软件对16 个城市进行初步聚类，同时检验该三类具有显著差异.为验证聚类效果，选取2017 年市城镇化率数据以及13 个代表城镇化程度的指标，利用提取的两个主要因子，对16 个城市分别计算因子得分，进一步验证城市的三种分类.验证结果为安徽省城市发展水平最好的六个城市为:淮南、铜陵、淮北、马鞍山、芜湖、合肥;其次为六安、安庆、宿州、亳州、阜阳;最后五个城市为蚌埠、滁州、宣城、黄山、池州.

第二步将提取的5 个因子与人均GDP 直接线性回归，拟合效果较差.

第三步将主因子与人均GDP 进行逐步回归，建立因子1、因子2、因子5、城镇化率与人均GDP 的回归模型，模型效果优异，方程显著成立.

3.3 建议

根据2003 到2017 年安徽省城镇化率与人均GDP 数据的回归分析，了解两变量之间是长期均衡的促进关系［20～22］.再根据市人均GDP 与城镇化率以及主因子的逐步回归模型，根据变量前系数为正，得到对于经济发展条件好的城市，若只推进城镇化基础建设，如增加城市常住人口比重或增加人均道路面积，并不能对经济的发展起到良好的促进作用.如何采取加强社会精神文明建设，减轻个人消费负担，增加个人财产净收入等措施来稳定城镇化率，是本文研究不足的地方.

近几年，安徽省的经济发展取得了令人瞩目的成绩，但是在推动城镇化过程中，仍然存在创新能力不足、区域发展不平衡不充分等问题.在后城镇化的过程中，要注重城镇化率质量的提升，推动城镇化与经济可持续发展.