新型超声波方形量水槽测流误差试验研究

付博，何新林*，陈金水，赵丽，邓小来，辛博

(1.石河子大学水利建筑工程学院，新疆 石河子 832000;2.河海大学计算机与信息学院，江苏 南京 210006;3.北京联创思源测控技术有限公司，北京 102200)

农业用水量占全国总用水量的61.3%～62.4%，农田灌溉用水量占农业用水总量的87.7%.因此，灌溉节水就成了国家节水的重中之重[1-3].为了有效管理并控制灌溉用水量，国家制定了一系列政策和措施对灌溉用水从水源至末级受水单元建立精准量水体系.“量准水”就成为灌区发展的重要建设内容之一，对于新型量水设施的研发与改进是目前灌区能够“量准水”的重点[4].谢崇宝等[5]认为目前对精度高、水头损失小、经济、适用性强的新型量水设施的研发和推广力度还不够.

末级明渠量水主要有2种方式：堰槽量水和仪器仪表量水[6-7].堰槽的发展自1888年BAZIN研制出长喉道量水槽[8]以来，量水槽种类越来越多，且测流精度能够得到保证，但也存在一些问题，以目前应用最为广泛的巴歇尔槽为例，SKOGERBOE等[8]指出巴歇尔槽与其他量水槽一样，安装时无论纵向还是横向都要保持一定的水平，才可以达到较好的量水效果.ABT等[9]指出由于量水设备的自身重量以及基础土壤经年累月的沉积，可能会导致巴歇尔槽的沉降对测流精度产生影响.ABT等[10]计算了纵向沉降对巴歇尔槽量水精度的影响，结果表明纵向沉降引起的坡度变化对巴歇尔槽测流精度有较大影响，当纵向坡度的变化范围为±5%时，巴歇尔槽流量曲线的最大相对误差为 28%；当横向坡度的变化范围为±5%时，巴歇尔槽流量曲线的最大相对误差为10%.PECK对淹没流情况下巴歇尔槽的一些参数进行整理，并发现当淹没度比较高时，流量和淹没度之间会呈现一种不连续性[11]，导致测流精度降低.仪器仪表量水方法中，以目前较为热门的超声波时差法量水为例，超声波时差法测流最早由德国RUTTEN提出[11]，其最大的特点是无接触式测量，这决定了它相比于其他传统流量计具有精度高、对水流流场影响小的优势[12].Instromet和Daniel等公司的产品测流误差(管道)小于0.5%，国内大连海峰的产品测流误差(管道)小于1%[13].王雪峰[14]认为超声波流量计对流场状态十分敏感，研究流场是提高精度的关键环节，然而国外对流场状态的研究较为完备.目前超声波测流研究在管道中应用较为广泛，而对明渠测流涉及较少，其主要原因在于明渠水流流场复杂多变.上述分析表明，堰槽量水的2个弊端：安装条件要求较高且实际施工难度大[15];量水槽在淹没出流条件下测流精度低[16].对超声波时差法测流而言，流场条件是影响测流精度的关键因素[17].

方形槽加设收缩段后测流的优点如下：① 方形槽的测流原理是流速面积法，可以避免量水槽在淹没出流条件下测流精度低的问题.② 收缩段具有提高过槽水流流场稳定性的优点，进而可提高声波的测流精度.

文中通过对比试验研究方形槽测流误差来源，并通过收缩段和水力学公式来提高新型超声波方形量水槽在非淹没出流条件下测流精度.期望为超声波方形量水槽在灌区的实际应用提供理论支撑，为灌区量水提供新思路.

1 结构与工作原理

1.1 超声波方形量水槽结构与工作原理

超声波方形量水槽由矩形铝合金壳体和超声波换能器等主要部件构成，超声波方形量水槽结构示意图如图1所示.

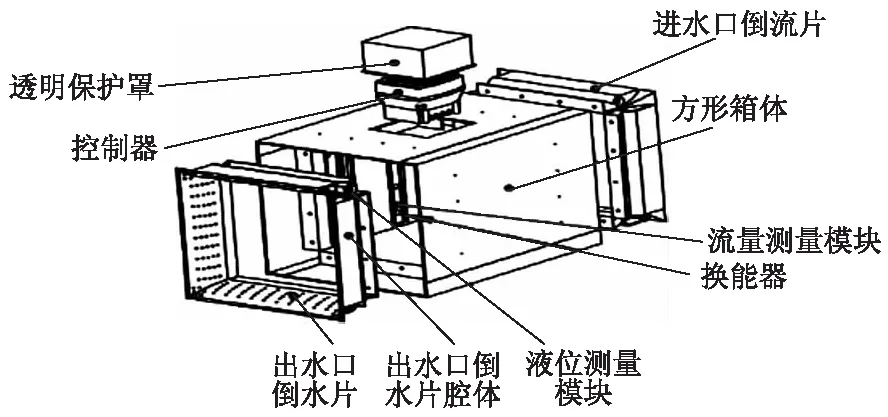
图1 超声波方形量水槽结构示意图Fig.1 Structure diagram of ultrasonic square measu-ring flume

图2为超声波时差法工作原理图.超声波方形槽的测流方法采用流速面积法Q=VA.流速测量部分，在矩形箱体内设置8层16个超声波换能器，每层换能器利用超声波时差法测量该层流速，8层流速取平均值后得到断面平均流速；水位测量部分，在矩形箱体侧面设置电容液位计，上方设置超声波水位计测量2组水位数据，在计算机上利用中位值滤波法得到断面平均水位.最后利用流速-面积法得出断面平均流量.

如图2所示，超声波换能器A，B是1对可轮流发射或接收超声波脉冲的换能器.设超声波信号在被测流体中的速度为c，顺流从A到B时间为t1，逆流从B到A时间为t2，外界传输延迟总时间为t0.则由几何关系可知

图2 超声波时差法工作原理图Fig.2 Schematic diagram of ultrasonic time difference method

(1)

(2)

由于c>>v2cos2θ，则

(3)

(4)

式中：c为超声波信号在被测流体中的速度，m/s；Δt为顺流、逆流换能器接收信号的时差，s；D为渠宽，m；v为断面平均流速，m/s；t1为顺流从A到B时间，s；t2为逆流从B到A时间，s；t0为外界传输延迟总时间，s.

1.2 收缩段流量公式推导

试验中发现流量小于0.1 m3/s时有收缩段的方形槽测流误差仍较大，为解决这一问题，利用文丘里原理推导出收缩段流量计算公式代替此流量条件下的方形槽测流.图3为试验布置与收缩段水力学公式计算断面划分示意图.恒定出流条件下标准收缩段出流，满足实际液体恒定总流能量方程和连续方程.

如图3所示，对断面1-1，2-2列能量方程与连续方程

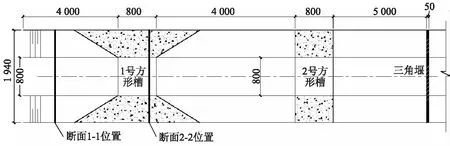
图3 试验布置与收缩段水力学公式计算断面划分示意图Fig.3 Schematic diagram of test arrangement and section division by hydraulic formula calculation of contraction section

(5)

A1v1=A2v2,

(6)

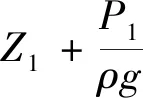
(7)

联立(5),(6),(7)，得出断面2-2处断面平均流速，即

(8)

(9)

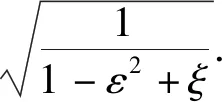
进而得出流量公式，即

(10)

2 试验设计与方法

2.1 试验设计

为探究新型超声波方形量水槽测流误差来源，试验于2019年6月在某智慧灌溉中心测控一体化闸门检测站进行.恒定出流条件下，渠道水流满足实际液体连续方程和能量方程，并且标准收缩段可利用式(9)进行测流.本试验在保证渠道恒定出流的条件下进行如下3组对比试验：有无收缩段方形槽与三角堰测流误差对比试验；收缩段公式计算流量与三角堰流量误差对比试验.单组试验重复3次，对流量、水位、流速等数据取平均值后进行对比分析.

智慧灌溉中心测控一体化闸门检测站具有完整的水循环系统，可保证闸门恒定出流.新型超声波方形量水槽测流误差试验布置如图3所示，试验渠道坡度为0、断面底宽0.80 m、上口宽1.94 m、高0.80 m的梯形渠道，沿水流方向依次布设2个800 mm×800 mm超声波方形量水槽及标准直三角堰，1号方形槽前后设置收缩角度为30°的收缩段，2号方形槽无收缩段.1号方形槽与闸门间距4 m；1号方形槽与2号方形槽间距4 m；2号方形槽与三角堰间距5 m.为满足不同流量条件下标准流量的监测，三角堰设置可更换的卡槽式安装方式，针对0.02～0.20 m3/s不同流量范围下，选择GB/T 21303—2007中3种不同规格的三角堰.

2.2 测定方法

2.2.1 收缩段流量公式计算相关物理量测量方法

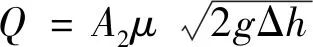
测量断面1-1，2-2水位时，取水面宽度的3个等分点，用带橡皮套的钢尺测量每个点的水位，并取平均值后得到该断面平均水深；断面2-2水面宽利用卷尺测得；测量断面1-1，2-2平均流速时，用LJ20旋桨式流速仪采用“三点”取样法计算断面平均流速，单点测量次数重复5次.

2.2.2 方形槽和三角堰测流相关物理量测量方法

根据闸门开启高度确定直角三角堰尺寸，待水流稳定后进行相关物理量的记录和测量.方形槽的显示面板可自动记录流量、水位、流速等物理量，抄录即可.计算三角堰标准流量需要测量堰上水头(自由出流)，上下游水位(淹没出流)等物理量由水尺直接读取获得.

3 流量误差结果对比分析

3.1 无收缩段方形槽与三角堰流量误差分析

6次不同闸门开度(6次不同的流量)条件下方形槽(无收缩段)与三角堰的流量误差曲线见图4a.无收缩段方形槽的整体测量误差较大，方形槽测流误差随流量的增大而减小.流量大于0.14 m3/s时方形槽测流误差低于8%，满足明渠堰槽量水测流误差要求.不同流量条件下，方形槽监测的槽内的流速分布见图4b,图中Qj为三角堰测流流量，Qf为无收缩段的方形槽测流流量，E为三角堰与方形槽的测流误差，h闸门为闸门开启的高度，Q为来水流量，n为方形槽的第n层换能器，t为时间，h液为水位高.

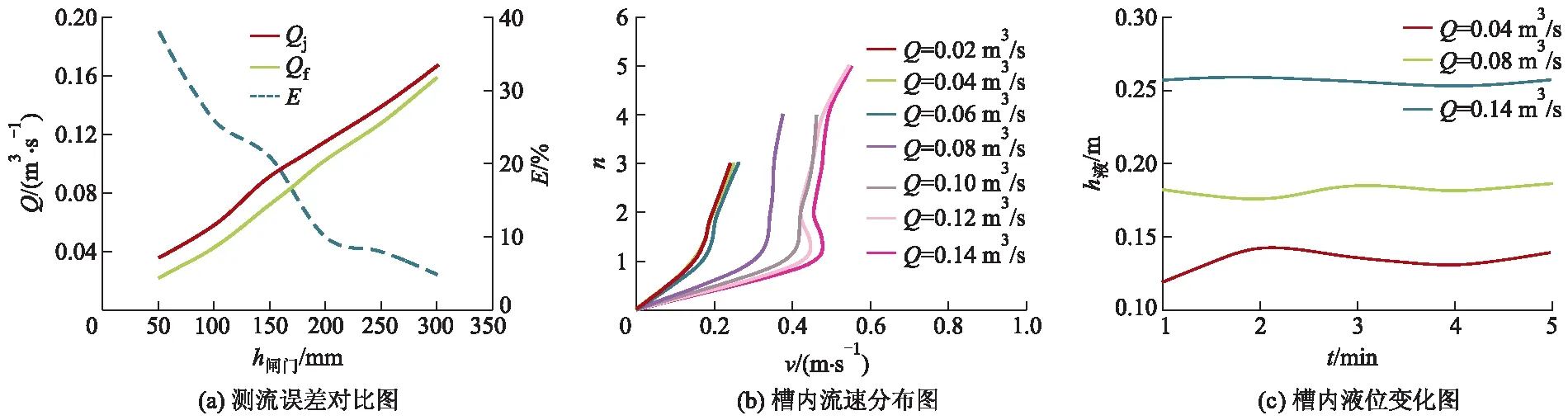
图4 2号方形槽试验数据分析图Fig.4 Analysis of No.2 square groove test data

流量小于0.08 m3/s时流速分布曲线与水力学二元明渠紊流流速分布(对数分布)相差较大，表明流速分布不均匀.流量大于0.08 m3/s时流速分布曲线与对数分布较为接近，表明流速分布较为均匀.横向观察图4曲线发现，随着流量的增大，流速出现不变的现象，表明换能器测流出现延迟现象.根据流速分布的均匀程度以及与三角堰的测流误差大小，水位变化选择3种流量条件(0.04，0.08，0.14 m3/s)监测，水位变化曲线见图4c.无收缩段方形槽内在同一流量条件下5 min内液位变化幅度大，且随流量的加大，液位变化幅度有减少的趋势.

分析流速、水位、误差3组曲线，发现随着流量的增大，流速分布更为均匀，水位趋于稳定，相对应的测流误差也有减小的趋势.表明无收缩段方形槽测流误差来自于流速分布不均匀，水位波动性大以及不稳定的水位流速条件导致换能器测速出现延迟问题.

3.2 有收缩段方形槽与三角堰流量误差分析

6次不同闸门开度(6次不同的流量)条件下方形槽(有收缩段)与三角堰的流量误差曲线见图5a，图中Qg为有收缩段方形槽的测流流量.方形槽的测流误差随流量的增大而减小，并且有收缩段的1号方形槽测流的整体误差较无收缩段的2号方形槽有明显的减少，整体误差低于16%.流量大于0.1 m3/s时测流误差低于8%，满足明渠堰槽量水测流误差低于8%的规范要求.方形槽槽内的流速分布图见图5b.方形槽内不同流量条件下的流速分布均与对数分布曲线接近，认为流速分布均匀.随着流量的增大，换能器的流速监测无不变的现象，认为换能器正常工作.水位变化曲线见图5c.有收缩段的1号方形槽内在同一流量条件下5 min内水位变化幅度明显减少，且0.14 m3/s流量条件下水位趋于定值，但小流量条件下水位波动仍较大.

图5 1号方形槽试验数据分析图Fig.5 Analysis of No.1 square groove test data

分析流速、水位、误差3组曲线发现，加设收缩段的方形槽的流速分布明显更加均匀，水位稳定性也明显提高，表明收缩段可较好地提高方形槽内流速分布均匀度，减少了流场因素对换能器工作的影响.但流量小于0.1 m3/s时水位波动仍较大，此时的测流误差也不满足明渠堰槽量水误差低于8%的规范要求，水位波动问题仍未得到解决.

3.3 收缩段公式计算流量与三角堰流量误差分析

加设收缩段的1号方形槽在流量大于0.1 m3/s的条件下，将方形槽的测流误差降低到8%以内，满足了明渠堰槽量水误差低于8%的规范要求.但在流量小于0.1 m3/s的条件下，由于水位波动，方形槽的测流误差仍不满足明渠堰槽量水误差应低于8%的规范要求.

计算流量与三角堰流量存在一定误差.通过水力学文丘里管道测流原理，推导出收缩段测流公式(式9).表1为流量公式计算表，表中W1-1为断面1-1水面宽，h1-1，h2-2分别为断面1-1,2-2平均水深，Q计为水力学公式计算流量.

表1 流量公式计算表Tab.1 Flow formula calculation table

计算流量误差曲线见图6.在流量小于0.12 m3/s的条件下公式计算流量误差低于8%以内，满足了明渠堰槽量水误差低于8%的规范要求.但随着流量的增大，收缩段出现淹没出流时，公式计算流量精度难以保证.

图6 公式计算流量与三角堰流量误差对比图Fig.6 Comparison diagram of flow error between for-mula calculation and triangle weir

3.4 不同闸门开度下3种测流形式流量差异分析

不同闸门开度下3种测流形式的流量对比见表2，表中Qf,Qg分别为无、有收缩段方形槽流量；Q计为水力学公式计算流量；Ef,Eg，E计分别为无收缩段方形槽、有收缩段方形槽以及水力学公式计算的流量与三角堰流量的误差.无收缩段的方形槽在闸门开度50～150 mm(标准流量低于0.1 m3/s)测流误差大.通过流速分布和水位曲线分析，表明此流量范围下流速分布不均匀；水位波动大以及由于流场不稳定导致的换能器出现不工作或延迟记录流速的现象是方形槽测流误差大的主要影响因素.

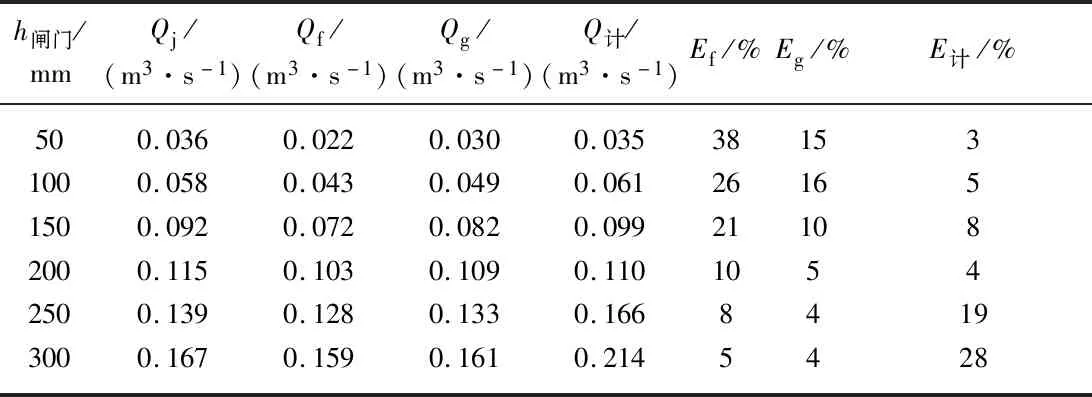
表2 不同闸门开度下3种测流形式的流量对比Tab.2 Flow comparison of three flow measurement forms under different gate openings

闸门开度大于200 mm(标准流量大于0.14 m3/s)时出现淹没出流现象，水位因素不再影响方形槽测流.分析此流量范围下的流速分布曲线，表明均匀的流速分布提高了方形槽测流精度.在不同闸门开度下，有收缩段方形槽相比于无收缩段方形槽的测流误差明显降低，通过流速分布和水位曲线分析，表明收缩段能够提高槽内流场稳定性；但在闸门开度小于150 mm(流量小于0.08 m3/s)时收缩段不能较好地解决水位波动大的问题，导致方形槽测流误差偏大.闸门开度大于250 mm后，由于出现淹没出流现象，水力学公式计算流量误差偏大.

4 结 论

1) 无收缩段的方形槽在淹没出流条件下测流误差低于8%；有收缩段方形槽在流量大于0.1 m3/s时，测流误差低于8%；流量小于0.1 m3/s时，收缩段流量公式计算误差小于5%.

2) 收缩段提高了方形槽内流速分布均匀度和水位稳定性，进而改善了换能器的工作环境；但流量小于0.1 m3/s时，流场对方形槽测流精度的影响仍较大，可利用收缩段测流公式计算代替方形槽测流来解决此问题.

3) 槽内流速分布均匀度、水位稳定性和换能器的工作状态是非淹没出流条件下新型超声波方形量水槽测流误差的主要影响因素.