基于响应曲面法的涡轮增压器废气阀门激光焊接工艺优化研究

褚自军，杨煜普

(1.上海交通大学电子信息与电气工程学院，上海 200240；2.上海菱重增压器有限公司，上海 201707)

0 引言

激光焊接是一种高效精密的焊接方法，它具有功率密度高，热影响区小，焊接变形小，速度快等优点，在汽车制造产业已被广泛应用。在涡轮增压器生产中，激光焊接技术也逐步被应用于废气阀门轴与阀杆孔的连接。如果废气阀门轴与阀杆的连接脱落，废气阀门就会失去有效控制，始终处于开启状态，最终就会由于增压压力不足而导致发动机动力不足、功率下降等。因此，提高废气阀门的焊接质量成为了涡轮增压器生产过程中需要解决的问题之一。

激光焊接的焊接质量受很多因素影响，包括焊接功率、焊接速度、离焦量和保护气流量等，优化焊接工艺参数是提高焊接质量的必经之路。在实际生产中，生产成本与周期限制了工艺参数实验的次数，需要在最少的实验次数内找到最优的工艺参数。另外，不同影响因素间的交互作用和激光焊接系统的非线性特征也会使找到最优工艺参数变得更加困难。因此，运用一种具有科学依据且有效的方法来进行实验和结果分析就显得极为重要。

实验设计(Design of Experiment, DOE)是以概率论和数理统计为理论基础，合理安排实验的一种科学的方法论，已广泛运用于生产制造业的产品质量改善、工艺流程优化方面。DOE方法分为因子设计、响应曲面法(Response Surface Methodology，RSM)和田口法。其中响应曲面法RSM主要应用于分析全因子实验不能确定和优化的二阶回归模型[1]。本文基于在前期试验中分析全因子设计时残差分析发现有弯曲现象后怀疑回归模型中存在二次项，进而决定采用RSM进一步实验。

1 响应曲面法简介

RSM是数学方法和统计方法结合的产物，用于对响应受多个变量影响的问题进行建模和分析，以优化这个响应[2]。RSM理论最早是由Box和Wilson在1951年提出的，是一种实验设计的最优化方法。RSM在考虑了实验的随机误差的同时，将复杂的未知的函数关系在小区域内用简单的一次或二次多项式模型来进行拟合。由于拟合的数学模型可精确的描述响应变量和因子之间的关系，所以可以通过数学模型来预测最优因子组合，从而得到理想的响应。响应曲面法是降低开发成本、优化加工条件、提高产品质量、解决生产过程中实际问题的一种有效方法。在实验设计、数据分析和实验预测方面具有很好的应用[3]。

设某一过程的响应变量为y，影响因子为X=(x1，x2，… ，xk)，RSM二阶回归模型的一般形式为：

(1)

式中xi和xj为自变量；β0为常数项；βi为线性项的回归系数；βii为平方项的回归系数；βij为因子交互作用项的回归系数；k为影响因子的数量；ε为误差。

2 实验准备与方案设计

废气阀门的焊接部位为阀门轴与阀杆孔的连接处如图1所示，本次实验中阀门轴的材料选择高温合金Inconel 713C，阀杆材料选择奥氏体不锈钢SUS304，轴孔配合为间隙配合。本次实验使用的激光器为TRUMPF公司的TruDisk 2000型碟片激光器，光束质量2 mm·mrad，波长为1 030 nm，最大输出功率为2 kW，功率输出稳定±1%。

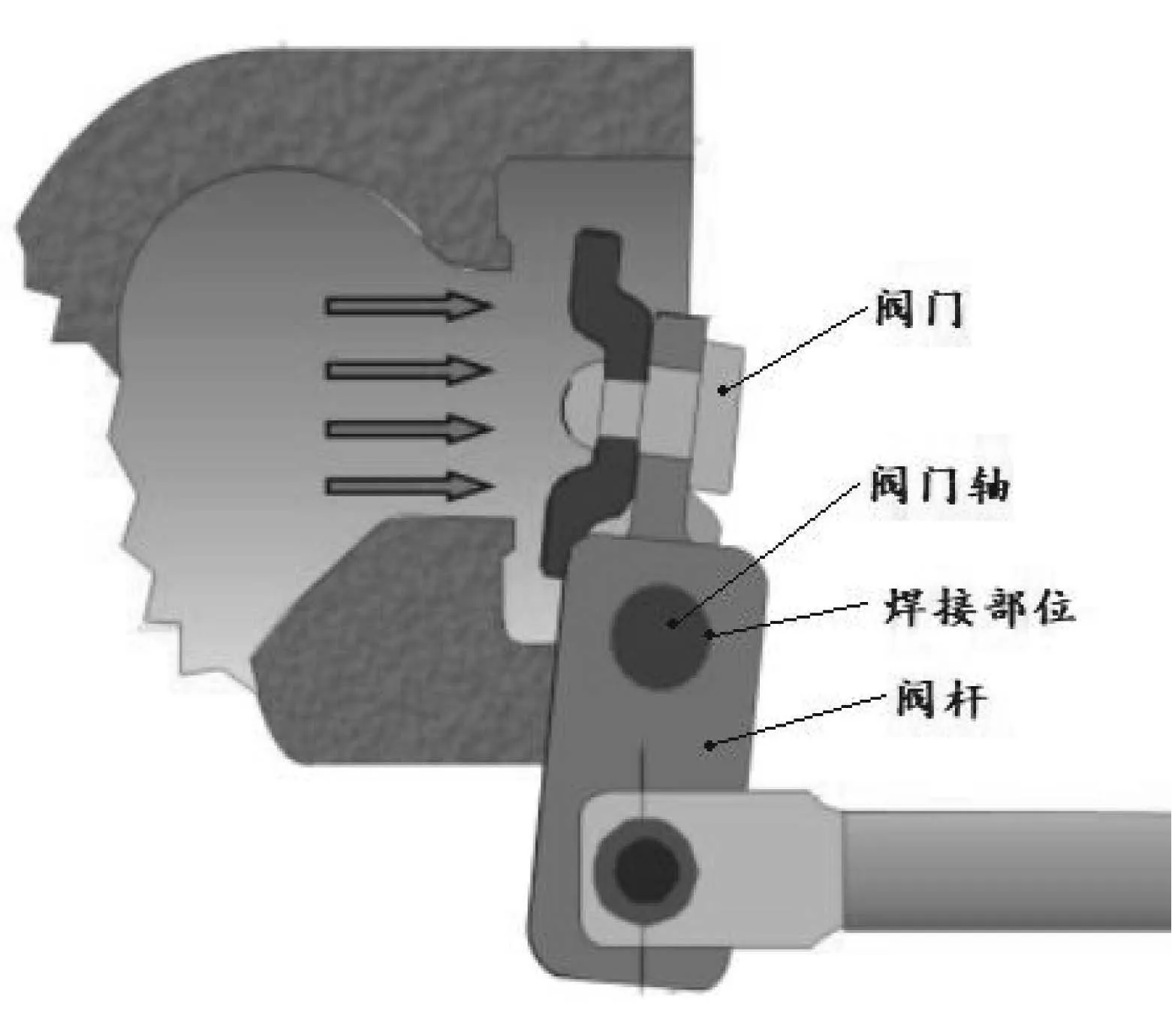
图1废气阀门焊接部位示意图

本次实验评价焊接质量的响应变量有三个，分别是熔接深度(D)、熔接宽度(W)以及内部缺陷数量(N)。影响焊接质量的因子选择焊接功率(P)和焊接速度(v)。离焦量为-2 mm，Ar气体流量为10 L/min，在本次实验中分别作为固定影响因子，由于焊接方式选择为连续焊，所以不考虑脉冲宽度和频率等因素。为了尽可能减少实验次数，本次实验每个因子选择两水平进行实验，DOE实验因子水平表如表1所示。

表1 DOE实验因子水平表

本次实验采用RSM的中心复合设计方法设计实验方案，选取立方体点4个，星号点4个，中心点5个，立方体点无重复，无区组划分，一共13次实验。为了尽量减少系统误差，将实验顺序影响也考虑在内，所以将实验顺序随机化。

3 实验结果分析与模型建立

实验样本在预定条件和方案下完成生产，在焊后的试件上取样，经过剖切、抛光和腐蚀后做成金相试样，并在金相显微镜下观察测量焊缝熔深、熔宽和内部缺陷情况。焊接内部缺陷主要分为裂纹和气孔，由于本次实验13组样本均未发现裂纹所以不作为此次实验的响应变量。最终得到实验计划和结果如表2所示。

得到实验结果后，首先使用Minitab软件来拟合熔深作为响应的回归模型，并对回归模型进行方差分析和模型拟合度评价。方差分析的目的是为了研究各因子对焊接质量是否有显著影响，定量分析各因子对实验结果的影响程度，然后再结合评估模型拟合度的统计量来判断拟合的回归模型是否合理，回归模型是否需要进一步修改。

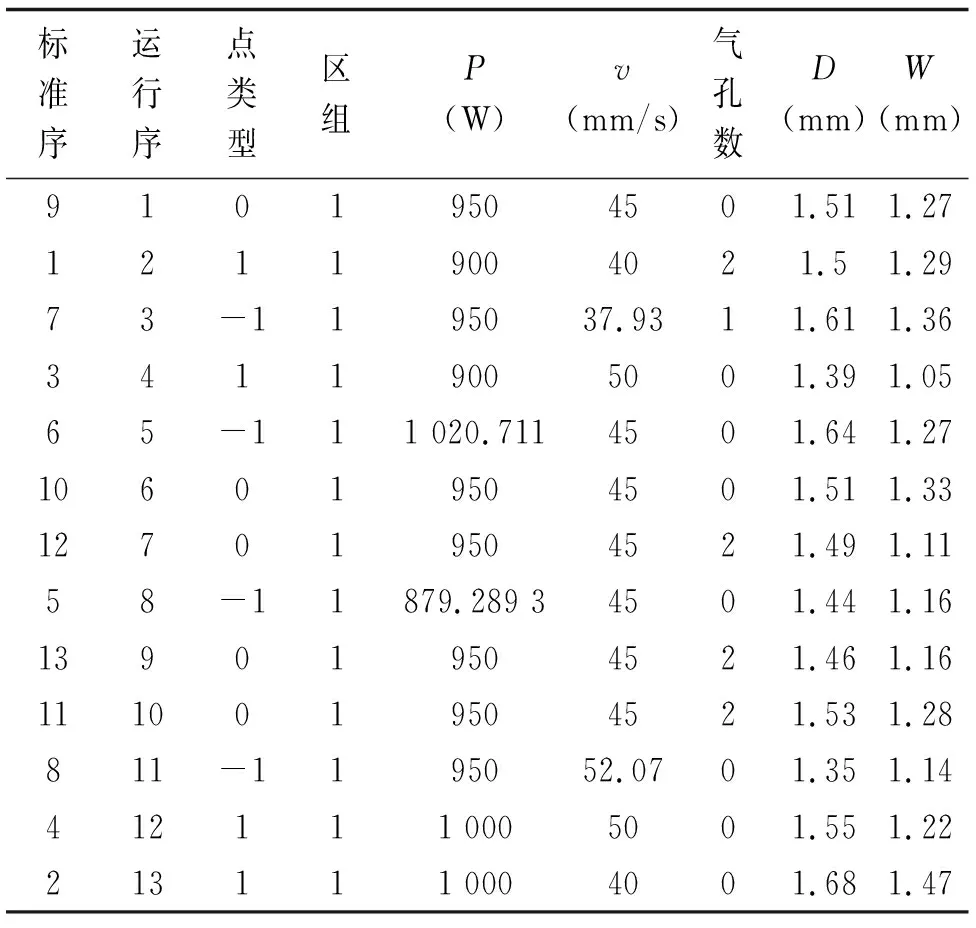
表2 DOE实验计划和结果表

方差分析输出结果见表3，表中SS表示误差平方和，MS表示SS除以自由度得出的均方误差，F值是由因子的MS除以误差的MS计算所得。

表3 熔深响应方差分析表

在方差分析表中，P值的大小表示回归模型及各因子的显著水平，如果P值小于0.05，则表示模型或参数有显著影响，如果P值大于0.05，则表示无显著影响。从表中可以看出，模型的P值小于0.05，说明该回归方程是显著的，表示模型总的来说是有效的；失拟的P值大于0.05则可以判断模型并没有失拟现象；功率P和速度v的P值均小于0.05，则表明这两个影响因子的一次项对熔深的影响显著，而两个影响因子的平方项和交互作用项的P值均大于0.05，则表明影响均不显著。

R2表示回归模型误差占总误差的百分比，由如下回归分析中的平方和分解公式可知，R2越接近100%表明回归模型与数据吻合得越好，式中SSModel表示模型的误差平方和，SSError表示误差的误差平方和，SSTotal表示总的误差平方和：

SSTotal=SSModel+SSError

(2)

(3)

(4)

(5)

表4 熔深响应的模型拟合度统计量表(模型修改前)

表5 熔深响应的模型拟合度统计量表(模型修改后)

修改完后的方差分析结果中P*P项的P值变更为0.03，小于0.05，所以可以判断为显著项。最终我们得到由P、v和P*P为变量，熔深为响应的数学模型如下：

D=9.96-0.017 94P-0.015 19v+0.000 010P2

(6)

最后，再通过观察熔深及焊接功率和焊接速度两个变量的残差图的残差散点的分布来判断模型是否正确。图2中正态概率图中的残差呈正态分布，在残差与拟合值图中残差随机波动，说明残差是等方差的，在残差与观测值顺序图中残差随机波动，说明彼此间独立。图3中可直观看出两个变量的残差的散点图在横轴上下随机波动，无弯曲趋势。由此说明该模型正确，无需再修改。

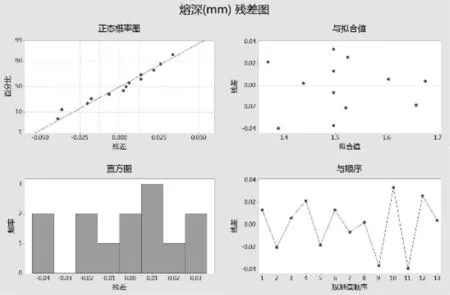
图2熔深残差图

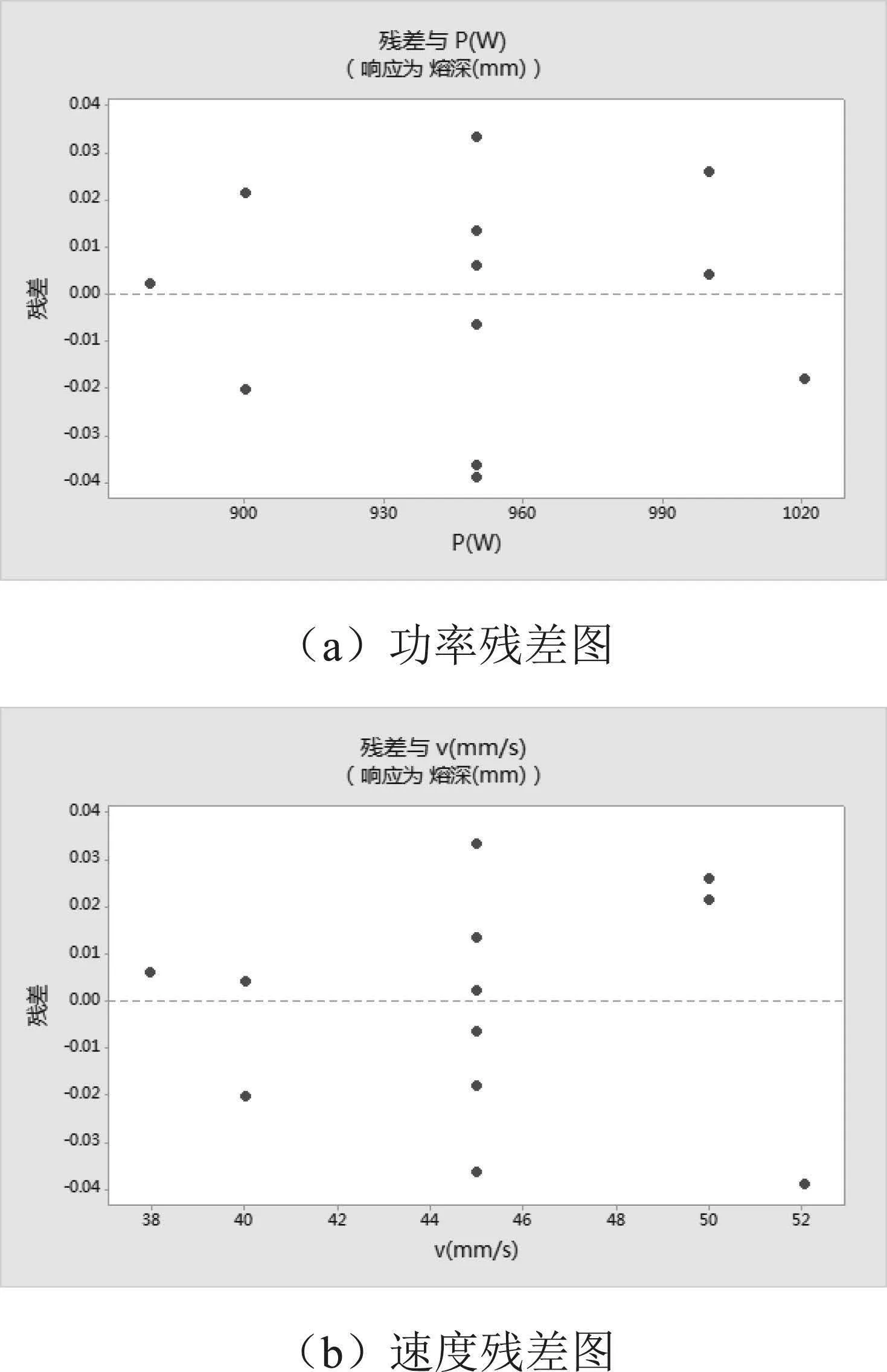
图3功率和速度的残差图

用相同的方法拟合熔宽，得到数学模型如下：

W=0.940+0.0126 4P-0.020 03v

(7)

在对气孔数作为响应进行方差分析时，发现各因子的P值均不显著(大于0.05)，表明本次实验中功率和速度都不是气孔数的显著影响因子，所以无法通过拟合模型进行预测。根据回归方程，得到了熔深和熔宽的因子主效应图(见图4)。显而易见，随着功率的提高，焊接熔深和熔宽呈增大的趋势，随着焊接速度的提高，焊接熔深和熔宽呈减小的趋势。

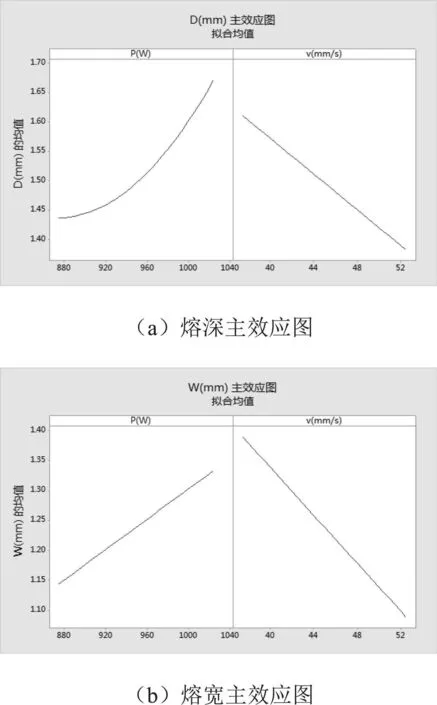
图4熔深和熔宽的主效应图

4 最优工艺预测与生产验证

此研究的目的是使用回归模型预测得到最理想的参数组合。在实际生产中，薄板的激光焊接熔深控制要求相对都非常严格。熔的太深容易导致焊穿，影响产品其他功能，熔的太浅又可能达不到所需的焊接强度。因此熔深一般都需要尽量控制在规定范围的中间区域。此次实验中熔深规定的范围是1.4 mm至1.7 mm，所以选择熔深的理想响应区域为中间区域1.5 mm～1.6 mm。由于尽可能降低热输入和减少过热区及母材高温停留时间，是减少和避免高温合金焊接结晶裂纹和液化裂纹的方法之一[4]，而相同熔深下熔宽越小，也表明焊接时的热输入也相对越小，所以需要控制熔宽尽量地小，熔宽的理想响应区域选择小于1.1 mm的区间。

基于已建立的熔深和熔宽模型借助Minitab软件输出等值线图，见图5。

图5熔深和熔宽的等值线图

图中理想响应区域由网格线标识，对比两个等值线图，显然两个理想响应区域不存在直接重合的区域，所以需要进一步综合分析，尽可能给出二者都最理想的预测参数。

利用Minitab软件的响应优化器功能，可以直接获得最佳参数点的设置及最佳响应值。将1.55 mm作为熔深的响应优化目标，期望熔宽尽量小作为熔宽的响应优化目标，权重都设为1，综合预测最优焊接参数，输出得到图6优化预测图。最优焊接参数组合为：P=1 020.543 1 W，v=52.071 1 mm/s，熔深的拟合值为1.55 mm，熔宽的拟合值为1.186 8 mm。

最后，在最优参数下进行5次重复性实验，测量的每单个值均落在95%的预测区间，数据平均值落在95%置信区间，见表6。结果证明模型是正确的，预测结果可信，此研究得出最优焊接参数可应用于实际生产中。

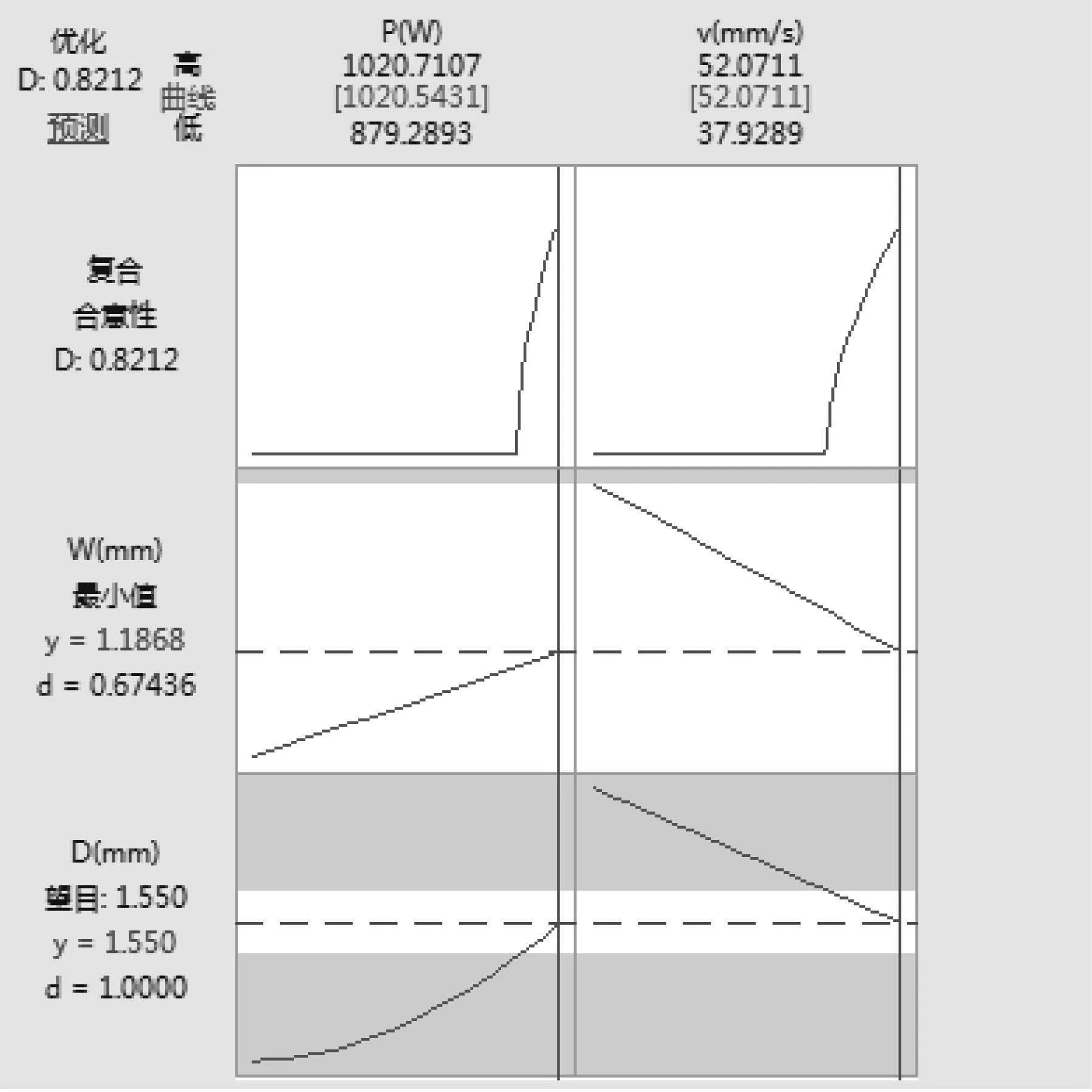
图6优化预测图

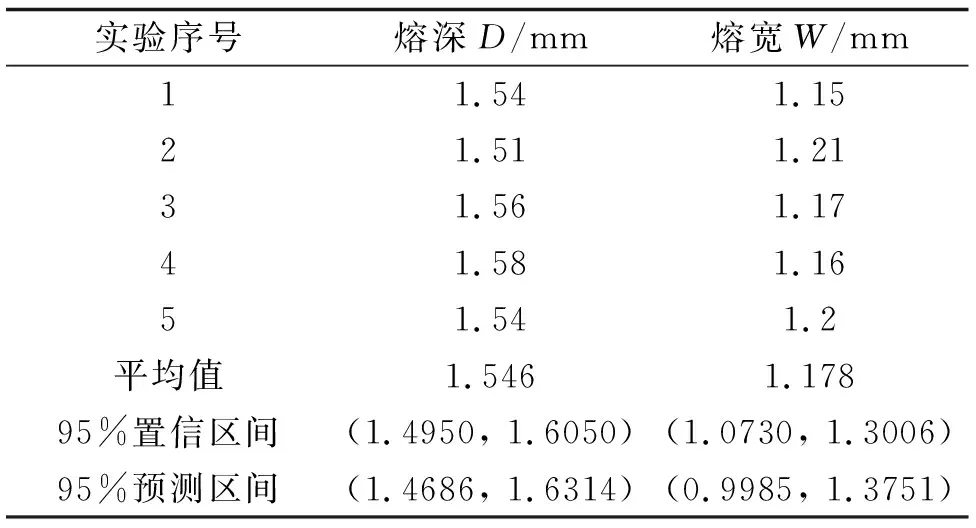
表6 最优参数验证表

5 结论

(1)成功拟合了涡轮增压器废气阀门激光焊接的熔深的二阶回归模型和熔宽的一阶回归模型。

(2)对得到的回归模型进行数理分析，发现焊接功率和速度都是显著影响因子，且随着功率的提高，焊接熔深和熔宽呈增大的趋势，随着焊接速度的提高，焊接熔深和熔宽呈减小的趋势。

(3)将熔深目标值1.55 mm和熔宽最小化作为响应的理想范围，综合预测最优焊接参数组合为：P=1 020.543 1 W，v=52.071 1 mm/s，并应用于生产中进行验证。结果证明模型正确，预测结果可信。响应曲面法在激光焊接工艺参数优化领域具有一定的指导意义。