初探平面框架模型在文坑水库塔式进水口计算中的应用

叶乔波

（三明市明兴水利水电勘察设计有限公司，福建 三明 365000）

在水工建筑物中，大体积不规则混凝土建筑物比较多。但是因为大体积不规则混凝土自身的原因，容易出现一些安全隐患。而如果出现了安全隐患，会对整个水利工程的效益成本带来巨大的影响。为了确保水利工程的效益并消除安全隐患，下面结合具体实例探讨了平面框架模型在水工建筑物结构计算中的应用。

1 工程概况

尤溪县文坑水库工程是三明市“十二五”烟草行业水源工程援建项目，其坝址位于尤溪县溪尾乡大宁村境内，所在流域为闽江尤溪流域华兰溪左支流纲纪溪上游河道上，是一座以灌溉为主兼顾供水等综合利用的水利工程，可承担溪尾乡的大宁、纲纪、埔宁等行政村耕地13630 亩灌溉的农业用水，同时作为溪尾乡的供水水源，供水目标为0.45 万t/d，并与现有供水水源实现水量互补以提高供水的安全保障程度。水库坝址以上流域面积26.1 km2，总库容285.23 万m3，属小（1）型水库，工程等别为Ⅳ等，主要建筑物级别为4 级，次要建筑级别为5 级，设计洪水标准重现期为30 a 一遇，校核洪水标准重现期为300 a 一遇。

2 基本资料

文坑水库工程由拦河坝、溢洪道、进水口、引水隧洞、灌溉渠道等组成。其中，进水口布置在拦河坝左岸上游约50 m 处岸坡下部，岸坡地形坡度约30°～40°，场地出露地层为南园组凝灰熔岩，呈弱风化，节理裂隙较发育，边坡未见滑坡体，崩塌体等不良物理地质现象，未见有危及进水塔边坡稳定的不良地质作用。进水口采用塔式单层布置，主要由进水喇叭口段、塔身、通气孔等组成。进水口底高程287.00 m，检修平台高程317.20 m。正常蓄水位312.50 m，死水位291.00 m，设计洪水位314.73 m，校核洪水位315.55 m，设计流量为1.41 m3/s，地震基本烈度为Ⅵ度，地震动峰值加速度为0.05 g。启闭房内布置两台QPQ-630 固定式卷扬机启闭机。

塔式进水口采用C25 钢筋混凝土，塔身横截面为矩形形状，顺水流方向长8.1 m，垂直水流向5.2 m，塔身高30.2 m。进水塔设2 道闸门，第一道为事故检修闸门，第二道为工作闸门，后设通气孔。检修闸门和工作闸门孔口尺寸为1.8 m×2.3 m（宽×高），事故检修闸门与工作闸门设0.8m 厚隔墙，工作闸门与通气孔设0.6 m 厚隔墙，通气孔为矩形孔，尺寸为1.6 m×0.8 m（长×宽），塔身横剖面见图1。

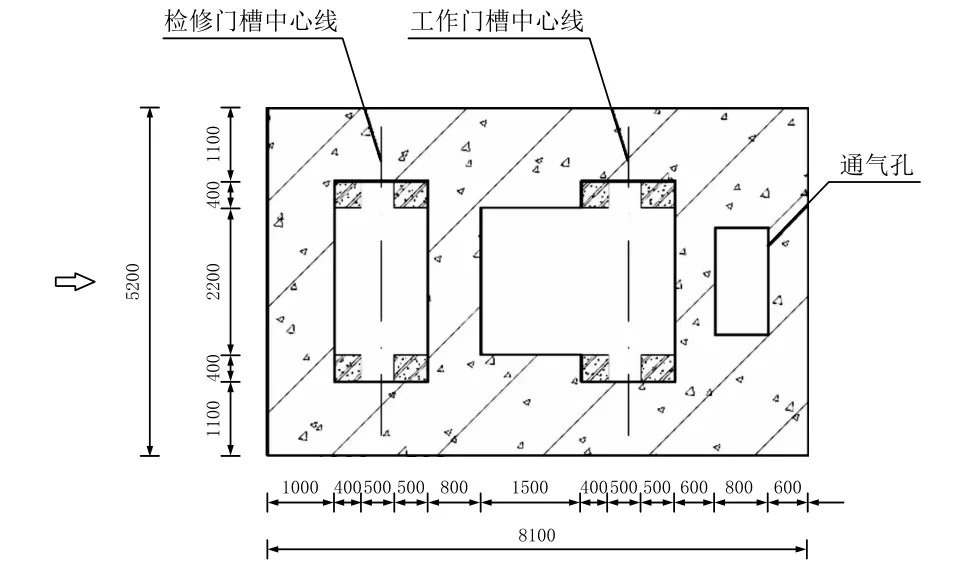
图1 塔身横剖面图

3 分析工况和计算模型

3.1 分析工况

文坑水库所在流域多年平均气温为18℃，地震基本烈度为Ⅵ度，为了分析简便，本次分析不考虑温度荷载、冰压力、风压力和浪压力等因素的影响。

根据文坑水库塔式进水口实际运行情况，运行状态为运行期和检修期。在运行期内，由于塔身沿着顺水流方向长度较短，可忽略水头损失，塔式进水口门槽内外水位等于库水位，塔身基本处在平压状态，故塔身内力主要由竖向平面内大体积混凝土引起的竖向压力为主，而由水平平面内水荷载产生的内力可忽略。在检修期，检修闸门关闭，工作闸门检修，由于检修闸门止水均为后止水，检修闸门门槽有水，工作闸门门槽无水，塔身内力虽仍以竖向压力为主，但由于检修闸门前后存在水位差，由水平平面内水荷载产生的内力不可忽略，其大小将直接关乎水平平面内混凝土的配筋。

本次分析在检修期内库水位处于正常蓄水位，检修闸门开启，工作闸门关闭情况下塔身在水压力作用下混凝土内力的工况。根据分析，最大的危险区域应该出现在事故检修闸门与工作闸门之间的隔墙的最低端，因此塔身的最易出现破坏的区域即在事故检修闸门与工作闸门之间的隔墙的下端部附近。

因此，在事故检修闸门与工作闸门之间的隔墙不利工况是在检修期，不在运行期；不利位置在隔墙的最低端。

3.2 计算模型

基于以上的分析结果将事故检修闸门与工作闸门之间的隔墙端部单独取出，作为配筋计算的设计依据，按照《水工混凝土结构设计规范》（SL 191-2008）杆件体系钢筋混凝土结构承载能力极限状态以及正常使用极限状态和非杆件体系钢筋混泥土结构的配筋计算原则之规定进行混凝土的应力配筋计算。

针对事故检修闸门与工作闸门之间的隔墙内力计算方法常见的有为一维固端梁模型、二维平面框架模型和三维有限元模型。其中，在塔式进水口计算模型中三维有限元方法认可度比较高，但三维有限元方法基于区域上的变分原理和剖分插值，待求未知数多，要求解的方程规模大，导致输入数据多，计算的准备工作量大，故其在一些小型水利工程中推广的程度较低。

本文通过对比一维固端梁模型和二维平面框架模型，找出适合小型塔式进水口的计算模型。

3.2.1 一维固端梁模型

在正常蓄水位情况下，截取高程为291.0 m～292.0 m 间的隔墙作为计算对象，将其视为两端固结于塔身的固端梁，计算跨度L0=4.1 m，梁高H=0.8 m，跨高比L0/H=5.1。

按结构力学法［1]算出隔墙的最大弯矩为Mmax=309.91 kN·m，最大剪力为Vmax=453.53 kN，计算简图见图2。

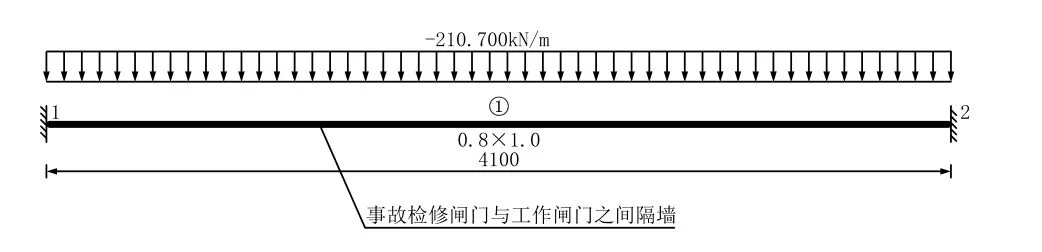
图2 一维固端梁计算简图

3.2.2 二维平面框架模型

在正常蓄水位情况下，截取高程为291.0 m～292.0 m 间的塔身作为计算对象，忽略二期混凝土，将其简化为单位高度内二维平面框架模型，杆件的截面高度按隔墙或边墙的厚度取，杆件的截面宽度为1.0 m，杆件的计算跨度按相邻隔墙或边墙中心线的间距取，杆件的断面尺寸及计算跨度特性见表1。

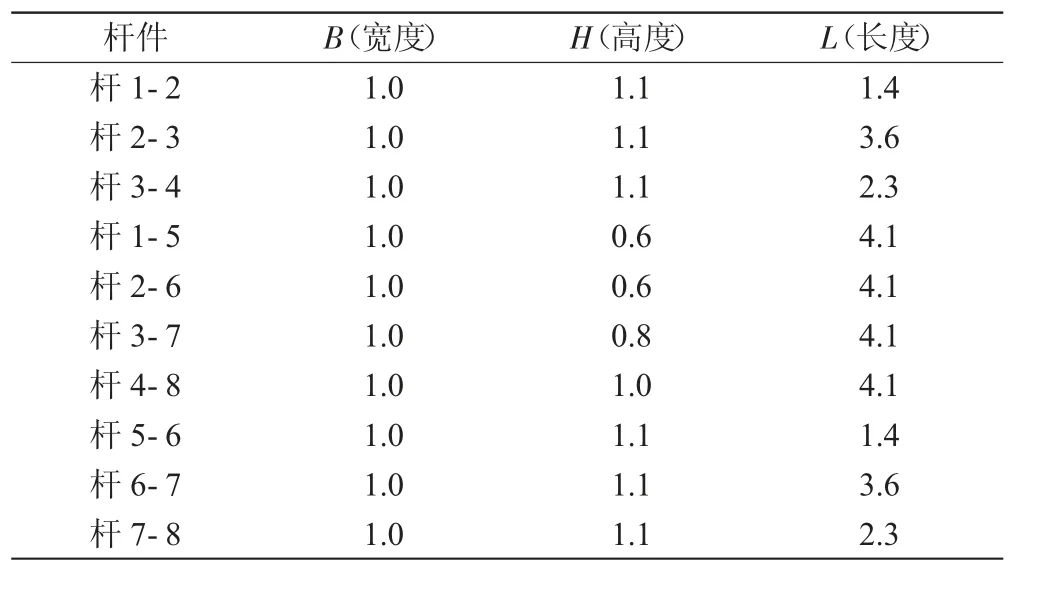
表1 断面尺寸及计算跨度特性表 单位：m

按结构力学法［1]计算出隔墙的最大弯矩为Mmax=315.45 kN·m， 最大剪力为Vmax=453.53 kN，计算简图见图3。

图3 二维平面框架计算简图

3.2.3 两种计算模型对比分析

在检修工况下，一维固端梁模型和二维平面框架模型计算得出最大剪力值相同，最大弯矩值之差ΔMmax=5.54 kN·m。随着检修闸门前后水位差的增大，最大弯矩值之差亦增大。通过和其他文献资料［2-6]对比发现，在检修工况下，事故检修闸门与工作闸门之间的隔墙所受的内力最大。

从模型上看，二维平面框架模型更能反映隔墙与周围构件的关系，与工程实际情况更贴合；从工程安全角度，二维平面框架模型弯矩计算值更大，且最大弯矩直接影响构件配筋的大小。综上考虑，推荐二维平面框架模型计算出最大弯矩值作为配筋计算的设计依据。

4 结论

（1）通过计算表明，在检修期，事故检修闸门与工作闸门之间隔墙受力状态与运行期不一样，在配筋和裂缝宽度验算计算中应加以注意。

（2）较三维有限元模型，二维平面框架模型在实际运用中计算方法简单，计算成果可靠；较一维固端梁模型，二维平面框架模型更加贴合实际和安全。二维平面框架模型计算方法原理清晰，计算过程明确，成果可靠。

（3）通过对比一维固端梁计算法和二维平面框架计算法的成果，得出二维平面框架模型具有相对优越性，对以后的小型水库塔式进水口设计工作有很好的指导作用，对工程施工有很好的指导作用。