钢管混凝土组合双肢柱偏压性能及设计方法

许力，郭子雄,2

(1.华侨大学土木工程学院，福建厦门，361021；2.华侨大学福建省结构工程与防灾重点实验室，福建厦门，361021)

框架结构在水平地震作用下主要依靠梁柱构件的屈服耗散地震能量，这会导致震后结构修复困难。鉴于此，MALAKOUTIAN 等[1]提出带联肢柱的框架结构体系，在该体系中，联肢柱由2根邻近的型钢柱通过若干钢梁连接而成，水平地震作用下，钢梁率先屈服耗能从而保护承重构件。截至目前，DIMAKOGIANNI等[2-4]开展相应的研究工作发现：通过合理设计布置，这种带“保险丝”的联肢柱框架结构体系能够实现理想的损伤控制。

为进一步提高构件承载力以及施工效率，本文提出一种新型钢管混凝土组合双肢柱(concrete filled steel tubular coupling composite columns，CCC)结构形式。CCC 的构造型式类似于格构柱，该柱以钢管混凝土(concrete filled steel tubular，CFST)作为柱肢，H型钢作为系梁，通过单边螺栓端板连接将2根柱肢与若干系梁组合成整体。CCC主要应用于水平力作用下以剪切变形为主的中低层框架结构。在正常使用状态时，CCC 为结构提供竖向承载力。地震作用下，系梁将承受侧向荷载引起的剪切作用而率先屈服耗能，减少主体构件的损伤，便于震后结构的加固修复。OU 等[5]开展了27根四肢钢管混凝土缀条柱轴压和偏压试验，发现长细比与偏心率是影响承载力的主要因素，且两者的影响基本上是独立的；聂建国等[6]以长细比为参数，对7 个钢管混凝土格构柱进行轴压试验，发现钢管混凝土格构柱各柱肢均处于小偏压受力状态；陈宝春等[7]提出了四肢钢管混凝土格构柱压弯承载力的实用设计方法；蒋丽忠等[8]提出了缀条K 形布置的钢管混凝土格构柱弹塑性极限承载力数值方法；HAN等[9]针对曲线形钢管混凝土格构柱，以初始曲率、长细比和缀件布置方式为主要参数，进行了轴压试验，发现缀条式格构柱的承载力显著高于缀板式格构柱的承载力；袁辉辉等[10-11]研究钢管混凝土格构柱在水平荷载作用下的力学行为。

CCC 作为框架结构的主要承重构件，了解其在压弯荷载作用下的基本结构特性具有重要意义。由于CCC 面外方向相当于2 个并列实腹柱，其设计计算方法与实腹柱的相似。因此，本文以偏心率和系梁数量为控制参数，设计4根CCC试件和4根对应的CFST试件，开展CCC面内方向的偏压试验和理论研究，并提出其承载力计算方法，可为工程设计提供参考。

1 试验概况

1.1 试件设计

试验共设计制作4 个CCC 试件以及与CCC 柱肢相同截面的1 个CFST 长柱和3 个CFST 短柱试件，CFST 试件用于研究CCC 组成部件的力学性能。试件采用实测截面宽度B和厚度t分别为180.0 mm 和5.8 mm 的Q345 冷弯方钢管。系梁采用高×宽×腹板厚×翼缘厚为250 mm×125 mm×6 mm×9 mm 的H 型钢。系梁与柱肢钢管之间采用8.8 级M16 单边螺栓连接。单边螺栓名义屈服应力和极限应力分别为640 MPa和800 MPa。使用扭矩扳手对单边螺栓施加190 N·m扭力。柱肢与系梁采用外伸端板式拼接节点，具体构造要求参考文献[12]。拼接节点的摩擦型抗剪承载力应不低于H 型钢系梁的剪切屈服强度：

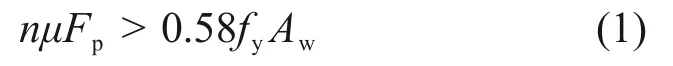
式中：n为螺栓数量；μ为钢板之间的摩擦因数；Fp为WANG等[13]提出的单边螺栓预紧力经验公式；fy为腹板的屈服强度；Aw为腹板面积。

实测混凝土28 d 立方体抗压强度均值fcu为71.2 MPa。钢管实测屈服强度为395 MPa，极限强度fu为530 MPa。H型钢采用Q235级钢材，实测屈服强度为344 MPa，极限强度为488 MPa。表1给出了试件主要设计参数，其中3个相同的单肢短柱试件统一表示为SSCC，SLCC 表示单肢长柱，CCC-x-y表示钢管混凝土组合双肢柱。对于CCC试件，编号中第1个数字表示系梁数量，第2个数字表示偏心率。

实际结构中，节点部位对CCC 端部有很强的约束作用。试验中，为保证试件端部足够刚度，在试件两端300 mm范围内四周焊接钢板，并在钢板围成的槽中浇灌混凝土，形成刚度很大的端部加载梁。试件尺寸如图1所示。

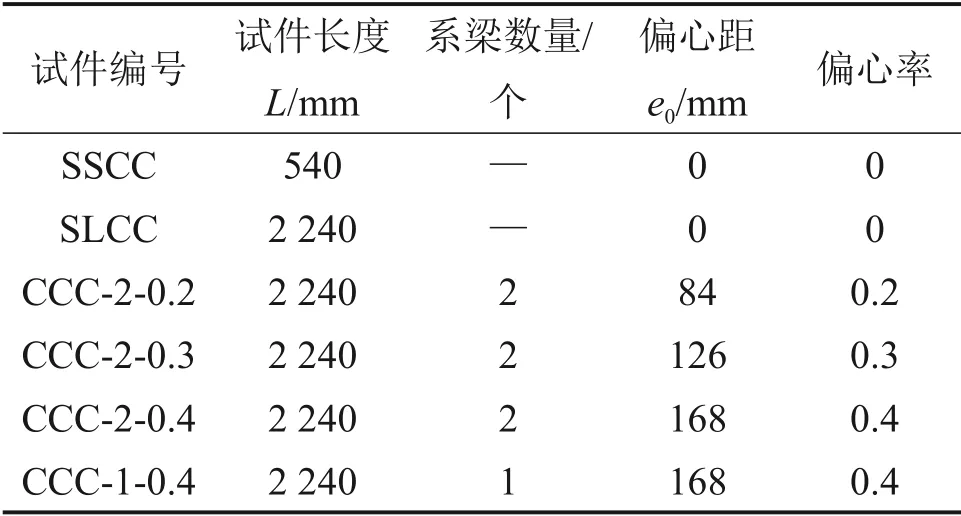
表1 试件参数Table 1 Parameters of specimens

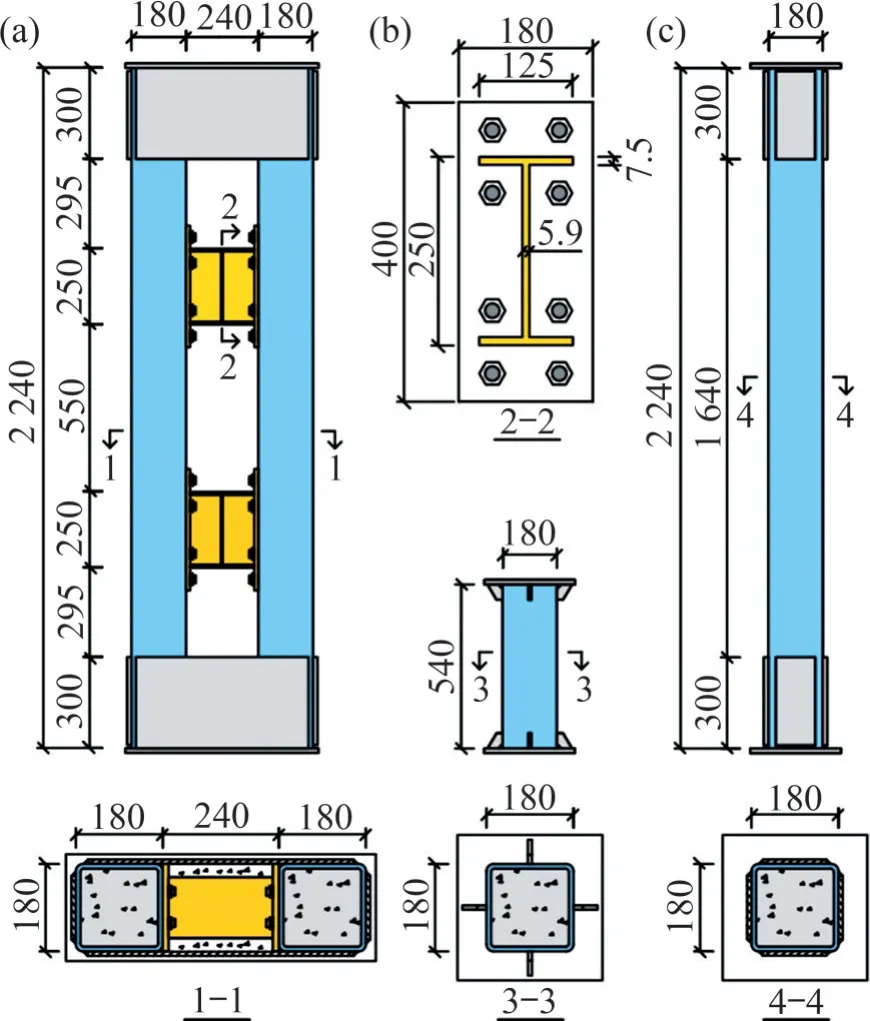
图1 试件尺寸Fig.1 Dimensions of specimens

1.2 试验装置

试验在福建省结构工程与防灾重点实验室10 000 kN电液伺服压-剪试验机上进行。除单肢短柱试件SSCC 直接加载外，单肢长柱试件SLCC 与组合双肢柱试件CCC 采用刀口铰加载。试验加载装置如图2所示。通过改变刀口铰与试件中心的相对位置实现不同的偏心率。正式加载前，首先对试件进行预加载，通过应变等数据检查是否物理对中。正式加载时，采用位移加载控制，加载速率为0.025 mm/s，当荷载下降到峰值荷载的50%或轴向变形超过50 mm时停止加载。

1.3 量测方案

图3所示试件典型的位移计和应变片测点布置。由图3可见：CCC试件前后两侧上下刀口铰转动中心之间各布置1个位移计，测量试件的轴向变形。沿2根柱肢高度四分点处各布置3个位移传感器，测量试件侧向变形。CCC试件的1/2柱高截面处以及柱肢与系梁相交的节点处钢管表面布置纵向应变片。此外，H型钢系梁腹板处布置1个应变花。CFST 试件在1/2 柱高截面处钢管表面中心布置纵向应变片。所有的力、位移和应变信号均通过电液伺服压剪试验机和DH3816数据采集仪自动采集。

图2 加载装置Fig.2 Text setup

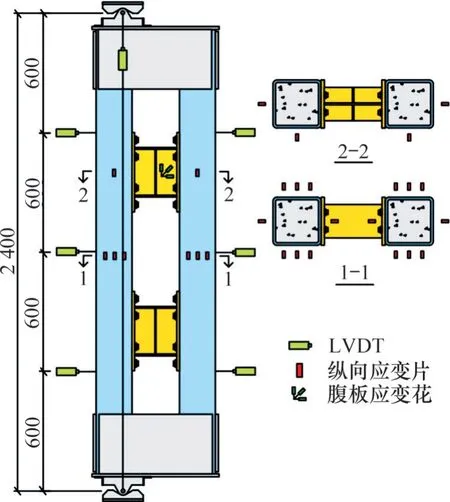
图3 位移计和应变片的测点布置Fig.3 Layout of LVDTs and strain gages

2 试验结果

2.1 试验过程及破坏特征

图4所示为CFST 柱试件破坏形态。由4(a)可见：3 个SSCC 试件的破坏过程近似相同。当荷载加载至83%峰值荷载时，钢管发生屈服。当荷载达到峰值荷载时，试件发出混凝土压溃的声音。当荷载降至95%峰值荷载时，钢管出现局部鼓曲。随后鼓曲程度不断加剧且管壁四面陆续出现新的鼓曲。当轴向加载变形δ达到20 mm 时，停止加载，此时试件承载力下降至峰值荷载的70%。

由图4(b)可见：由于长度效应的影响，当荷载加至88%峰值荷载时，试件SLCC表现出轻微的整体弯曲变形，此时最大侧向变形Δ约为4.4 mm。当荷载达到峰值荷载时，试件在1/3柱高处凹侧钢管翼缘出现局部鼓曲。由于二阶效应的影响，试件在随后的加载中侧向挠曲变形不断增大，钢管鼓曲的范围从初始的凹侧面钢管翼缘逐渐扩大到两侧腹板，最终形成塑性铰。当轴向加载变形δ达到30 mm 时，停止加载，此时试件承载力下降至峰值荷载的36%。试件表现为整体弯曲失稳破坏。

图4 CFST柱试件破坏形态Fig.4 Failure modes of CFST specimens

图5所示为CCC 试件破坏形态。下面以试件CCC-2-0.4为例介绍CCC在偏压荷载作用下的试验现象。当荷载加载至79%峰值荷载时，由于荷载的偏心作用，2根柱肢承担的荷载不均匀，近载侧柱肢钢管率先发生屈服。当荷载达到峰值荷载时，此时试件整体变形不明显，最大侧向变形Δ约为5.0 mm。当荷载降至92%峰值荷载时，近载侧柱肢1/2柱高附近的钢管出现局部鼓曲。随着轴向加载变形δ增加，近载侧柱肢钢管鼓曲程度加剧且不断产生新的鼓曲。CCC 柱近载侧柱肢在破坏区域发生明显压缩变形且伴随着多处局部鼓曲，其破坏特征与对应CFST短柱轴压破坏特征相似。与此同时，试件整体侧向挠曲变形不断增大，在δ到达14 mm 时，远载侧柱肢钢管外侧翼缘发生受拉屈服。最终试件的破坏表现为整体的面内弯曲变形和近载侧柱肢钢管的多处局部屈曲，在本文参数研究范围内，CCC 试件的破坏主要受面内失稳控制，面外变形很小。

图5 CCC试件破坏形态Fig.5 Failure modes of CCC specimens

通常，2 个系梁试件的破坏区域集中在中部2个相邻系梁之间，而试件CCC-2-0.2发生在试件下部系梁与加载梁之间，这可能是由于混凝土材料性能沿试件高度不均匀引起的。单个系梁试件的破坏区域集中在柱中部以下300 mm 位置处。此外，试验过程中均未出现焊缝断裂或螺栓拔出等局部破坏现象。

2.2 轴向荷载-变形曲线

图6所示为所有试件的轴向荷载-变形曲线。各试件特征点结果见表2。由图6和表2可知：

1)由于混凝土的压溃，SSCC试件在峰值荷载之后承载力出现突降。当承载力降至68%峰值荷载时，由于钢管的约束作用，试件维持残余承载力近似不变甚至略有上升至加载结束。

2)随着试件长细比增大，SLCC试件的峰值荷载相较SSCC 试件下降12.7%。受二阶弯矩的影响，SLCC 试件在峰值荷载过后承载力不断下降，无平台段。

3)不同偏心率的CCC 试件曲线弹性段的斜率接近。在偏心率为0.4的条件下，单个系梁试件曲线的初始斜率略低于2个系梁试件的初始斜率。

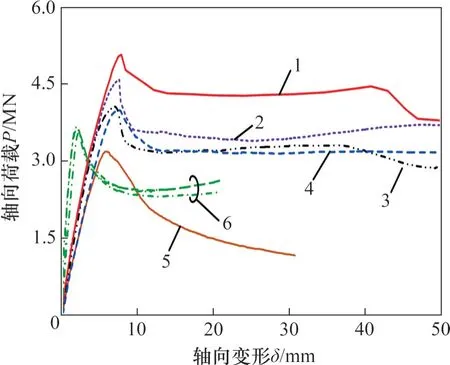
图6 轴向荷载-变形曲线Fig.6 Axial load-deformation curves

4)随着偏心率增大，CCC 试件峰值荷载明显下降。当偏心率从0.2增大到0.4时，承载力降低约20%。系梁数量对试件承载力无显著影响，CCC-1-0.4 试件峰值荷载相对CCC-2-0.4试件的峰值荷载仅低1.7%。

5)CCC试件在偏压荷载作用下的轴向荷载-变形曲线特征与其对应的CFST短柱轴压曲线特征相似，即超过峰值荷载后，承载力急剧下降，在轴向变形达12～14 mm 处，曲线出现拐点，继续加载，试件残余承载力基本维持稳定。取δ为14 mm处的轴向荷载为试件的残余荷载，CCC 试件的残余荷载相对峰值荷载的比值约为79%。但在CCC-2-0.2 试件中，该比值相比其他试件的比值高，这可能与其破坏位置有关。

表2 试验与有限元分析结果Table 2 Experimental and FEA results

2.3 1/2柱高截面纵向应变

试验加载过程中，量测钢管截面的应变，监测各柱肢的受力状态。图7所示为试件CCC-2-0.4在1/2柱高截面处近载侧柱肢与远载侧柱肢钢管纵向应变分布随荷载变化的发展过程。从图7可知：

1)近载侧柱肢与远载侧柱肢截面应变均满足平截面假定。

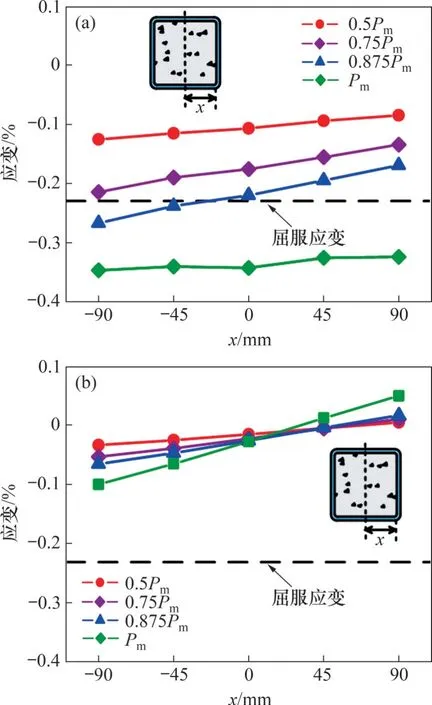
图7 1/2柱高截面纵向应变分布(试件CCC-2-0.4)Fig.7 Distribution of longitudinal strain at the mid-height(specimen of CCC-2-0.4)

2)近载侧柱肢全截面受压，应变梯度相对轴向应变较小，柱肢近似处于轴压状态；远载侧柱肢所受轴力较小而弯矩相对较大，加载过程中弯矩不断增大，处于偏压状态。

3)近载侧柱肢在峰值荷载时截面平均纵向应变为3 360 με，3个SSCC轴压短柱试件在峰值荷载时截面纵向应变平均值为3 455 με，说明CCC试件在峰值荷载时近载侧柱肢基本达到其轴心抗压强度。

3 有限元分析

3.1 有限元模型

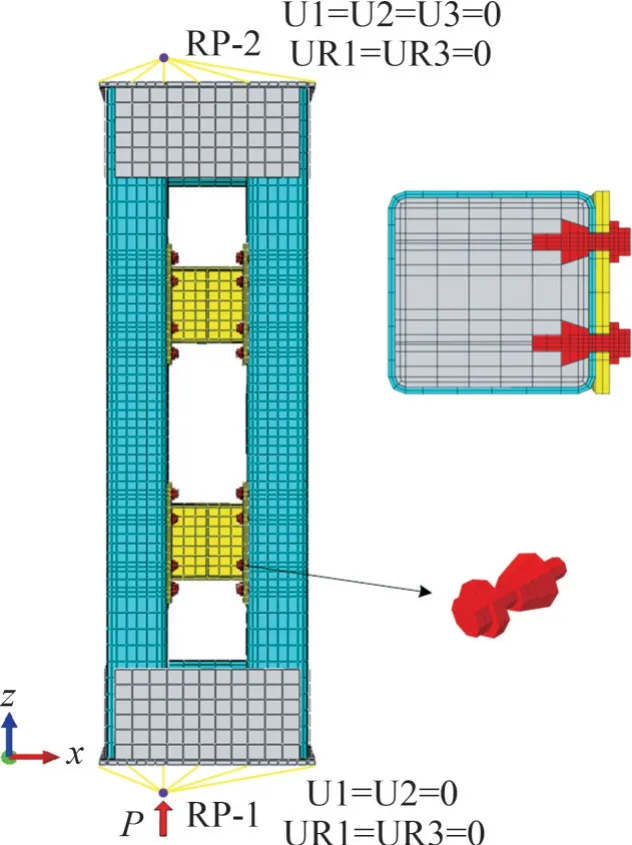
图8 有限元模型单元划分和边界条件Fig.8 Boundary condition and elements of finite element model

图8所示为采用有限元软件ABAQUS 建立的CCC 试件有限元模型。钢管、混凝土、H 型钢系梁以及单边螺栓等组件均采用实体单元(C3D8R)建模。采用文献[14]建议的五段式弹塑性模型模拟钢材的应力-应变关系。由于试验采用的是冷弯方钢管，因此，根据文献[15]考虑钢管弯角部分的应力强化。约束混凝土的本构模型采用混凝土塑性损伤模型，其受压应力-应变关系[16]为：

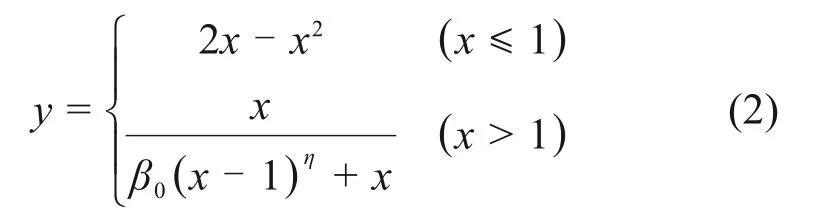
式中：x=e/e0，y=s/f′c，f′c为混凝土圆柱体抗压强度；β0和ε0是与约束系数θ相关的参数，具体取值参照文献[17]；θ=Asfy/(Acfck)；Ac和As分别为内填混凝土和钢管的面积；fck为混凝土抗压强度标准值。

模型中端部盖板与钢管等焊接连接采用绑定约束。混凝土与钢管、单边螺栓与混凝土、连接件与钢管等实体之间分别设置接触对，采用“硬接触”模拟接触面之间的法向行为，采用库仑摩擦模型模拟接触面之间的切向行为。其中，混凝土与钢材之间的摩擦因数取0.40[17]，钢材之间的摩擦因数取0.35[12]。单边螺栓的预紧力通过“降温法”[18]施加在螺杆上。试件两端在刀口铰转动中心处分别设置参考点(RP-1 和RP-2)，参考点与对应的端板面耦合，参考点面内转动自由度(UR2)不设置约束，其余自由度均设置约束。在加载底板的参考点上施加竖向位移模拟加载。

3.2 模型验证

图9所示为CCC-2-0.3 试件的试验和有限元模型破坏形态对比。从图9可见：试验和有限元模型破坏形态均表现为整体面内弯曲变形，破坏位置均集中在近载侧柱肢中部。图10所示为有限元计算所得的CCC试件的轴向荷载-变形曲线与试验曲线的对比。由图10可知：二者整体吻合良好，有限元模型得到最大承载力计算值与试验最大承载力比值的平均值为0.989，标准差为0.011。因此，有限元模型能够较好地模拟组合双肢柱在偏压荷载下的受力行为以及预测其承载力，可进一步分析试件的参数影响。

3.3 系梁受力特点

图9 试验与有限元模型的破坏对比(CCC-2-0.3)Fig.9 Comparison between experimental and FEM failure modes(CCC-2-0.3)

偏压荷载作用下，CCC 构件发生弯曲变形。由于变形引起附加弯矩，从而产生平行于柱截面的横向剪力V=dM/dz，该剪力由系梁承担。此外，钢管混凝土柱肢在轴向力作用下的侧向膨胀受到H型钢系梁的约束。图11所示为试件CCC-2-0.4在峰值荷载时刻的系梁Mises应力云图以及腹板的主应力矢量图。由图11(a)可见：除了腹板右下角部集中较大应力之外(最大Mises应力为163 MPa，该值小于腹板的屈服应力)，其余位置应力较小，H 型钢系梁处在弹性阶段。这符合系梁的设计理念，即正常使用工况下保持弹性。由图11(b)可见：受力单元主要集中在左下侧区域，除右下角部若干单元处于双向受力外，其他单元基本处于单向受压状态。腹板的压力沿着对角线方向传递，腹板的作用类似于斜压杆。

3.4 柱肢受力特点

图12所示为CCC 试件在偏压荷载作用下的受力分析。由图12可知：CCC 试件在偏压荷载作用下承受轴心压力P和弯矩P(e0+Δ)的共同作用。其中，轴心压力P由近载侧柱肢轴力Pl及远载侧柱肢轴力Pol共同承担；弯矩P(e0+Δ)则通过2 根柱肢截面弯矩Ml，Mol以及柱肢轴力产生的抵抗力矩(Pl-Pol)h来平衡。

图13所示为各试件在峰值荷载时刻不同组分承担的轴力和弯矩。由图13可知：

1)近载侧柱肢承担较大的竖向荷载；近载侧柱肢的承载力能近似发挥到其轴心受压强度的98%；

图10 试验与有限元轴向荷载-变形曲线对比Fig.10 Comparison between experimental and FEM axial load-deformation curves

图11 峰值荷载时刻系梁受力状态(CCC-2-0.4)Fig.11 Stress state of connector beam at the peak load(CCC-2-0.4)

2)远载侧柱肢承担的轴力随偏心率增大而降低；

3)外荷载产生的弯矩主要由两柱肢轴力产生的抵抗力矩来平衡，截面弯矩承担的比例仅占7%～9%；偏心率及系梁数量对柱肢截面弯矩承担的比例无明显影响。

3.5 参数分析

通过有限元模拟，分析长细比和钢管壁厚对组合双肢柱偏心受压承载力的影响规律。

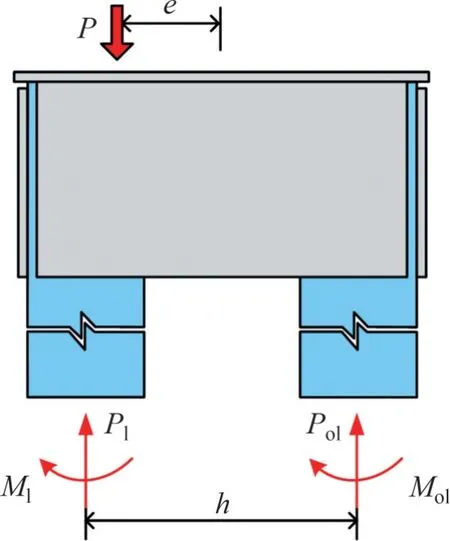
图12 CCC试件在偏压荷载作用下的受力分析Fig.12 Mechanical analysis of CCC sample under eccentrical loading

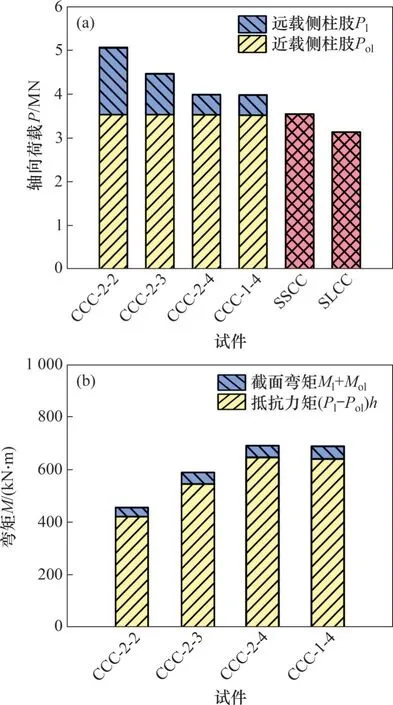
图13 峰值荷载时刻不同组分的内力分配Fig.13 Internal force distribution among different components at the peak load

为研究长细比对组合双肢柱承载力的影响，同时考察偏心率和长细比二者之间的关系，选择3种长细比分别计算5种不同偏心率下的承载力。图14所示为不同长细比下强度降低系数与偏心率的关系。强度降低系数为CCC 试件在偏压荷载作用下的峰值荷载Pu与2 根柱肢轴心受压强度之和2P0的比值。由图14可知：

1)随着偏心率增大，CCC 试件承载力近似呈线性降低。

2)随着长细比增大，承载力有一定程度降低。同一偏心率下，长细比从11.1增大到18.5，试件承载力降低约5%。

3)不同长细比下，强度降低系数-偏心率曲线基本平行，表明偏心率和长细比对承载力的影响是独立的，普通钢管混凝土格构柱的试验结果同样也发现这一规律[5]。

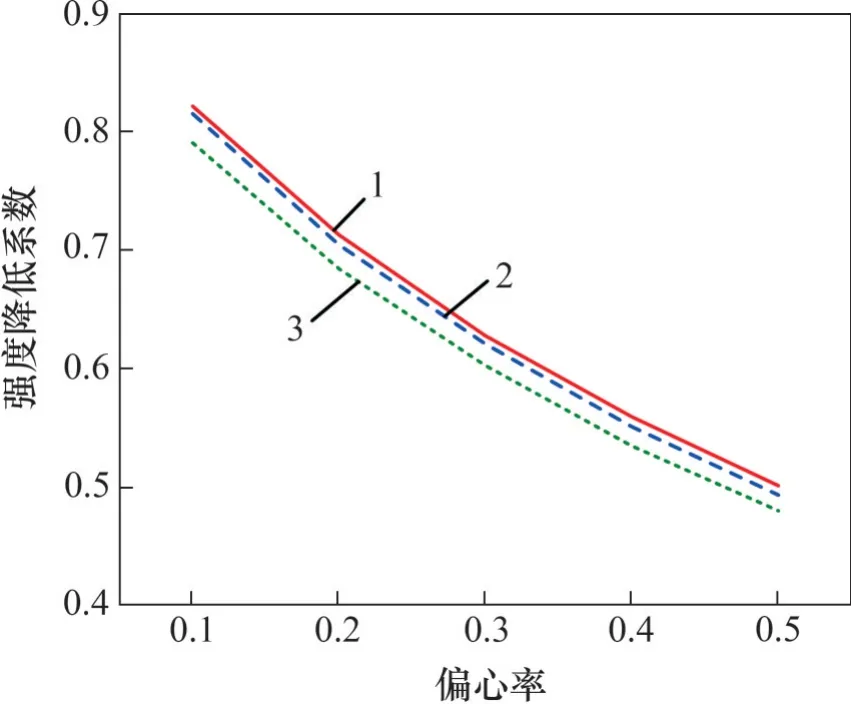
图14 强度降低系数-偏心率关系曲线Fig.14 Strength reduction factor versus eccentricity ratio curves

以试件CCC-2-0.2为基准模型，保持其他参数不变，改变钢管壁厚t，考察不同钢管壁厚对CCC构件的轴向荷载-变形曲线的影响，图15所示为不同壁厚CCC 试件的轴向荷载-变形曲线。由图15可知：随着钢管壁厚增大，试件轴向荷载-变形曲线的初始刚度增加，同时试件峰值荷载得以提高。随着壁厚增加，残余荷载相对峰值荷载的下降幅度有所减小。对于柱肢钢管壁厚为5.8，8.0，11.0和13.0 mm的试件，其残余荷载相对峰值荷载的下降幅度分别为23.3%，18.7%，12.4%和9.6%。以上变化的原因主要是由于增加钢管壁厚一方面提高构件含钢率，从而提高构件刚度和承载力，另一方面提高约束系数，核心混凝土的塑性相应增加，使得曲线下降段趋于平缓。

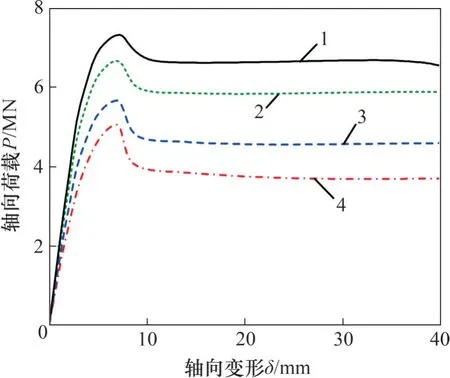
图15 不同壁厚CCC试件的轴力荷载-变形关系曲线Fig.15 Axial load-deformation curves of CCC specimens with different steel tube thickness

4 偏压承载力计算

影响CCC 偏心受压构件承载力的主要因素是偏心率和长细比，且二者之间存在近似独立的关系，故本文采取文献[20]给出的双系数乘积计算公式求解组合双肢柱的偏压承载力：

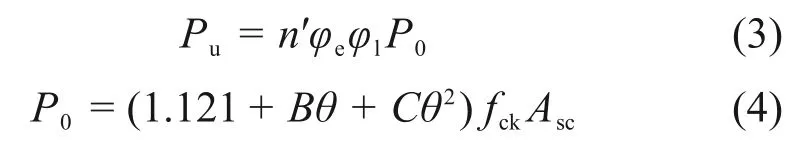
式中：n′为柱肢数量；P0为单根柱肢的轴心受压强度；θ为约束系数；B和C为截面形状对约束效应的影响系数；φe为考虑偏心率影响的整体承载力折减系数，当偏心率＜0.5 时，φe=1/(1+2e0/h)；φl为考虑长细比影响的整体承载力折减系数，根据长细比查表或计算得到φl，具体方法参考文献[19]。

对于格构式构件，柱肢之间非连续实体相连，构件的稳定性受剪切变形影响不可忽略[20]。采用换算长细比代替名义长细比计算稳定系数，根据文献[9]，换算长细比的计算公式为：

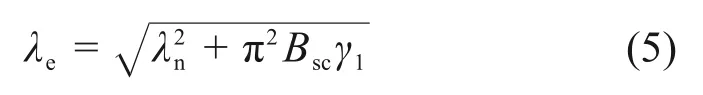
式中：λe为等效长细比；λn为名义长细比；γ1为单位剪切角，即构件的剪切刚度；Bsc为CCC 试件的组合轴压刚度，Bsc=2EsAs+2EcAc，其中，Es和Ec分别为钢管和钢管内混凝土的弹性模量，As和Ac分别为单肢钢管和钢管内混凝土的截面面积。

对于CCC 试件，假定系梁与柱肢之间的连接为刚性连接。由于柱肢截面宽度与型钢系梁高度比较大，相交部分形成较大尺寸的节点区，可将CCC 试件视作壁式框架。图16所示为壁式框架模型的计算单元剪切变形。出于简化考虑，假定刚域范围取至整个节点区，反弯点在各壁式梁、壁式柱中点。

图16 计算单元剪切变形Fig.16 Shear deformation of calculation unit

由图16可得单位剪切角γ1计算式如下：

式中：a为壁式框架节点刚域的高度；l1和l2分别为计算单元上反弯点和下反弯点到刚域的距离；Δb1和Δb2分别为计算单元上反弯点和下柱肢在1/2单位力下产生的侧向变形；Δv为系梁剪切变形引起的计算单元侧向变形；Bs=EsIs+EcIc，其中，Is和Ic分别为单肢钢管、钢管内混凝土的截面惯性矩；BG=GsAs+GcAc，其中，Gs和Gc分别为钢管和钢管内混凝土的剪变模量；GH与AH分别为H 型钢腹板的剪切模量与面积。

表3所示为承载力公式计算值Pu,c与试验值Pu的对比。图17所示为承载力公式计算值Pu,c与有限元计算值Pu,FEM的对比。由表3和图17可知：Pu,c/Pu的平均值为0.820，Pu,c/Pu,FEM的平均值为0.834，计算值较吻合但偏保守。主要原因是式(4)低估了钢管混凝土短柱轴压强度承载力，其计算值P0与单肢短柱试件SSCC 极限强度试验值的比值为87.9%。

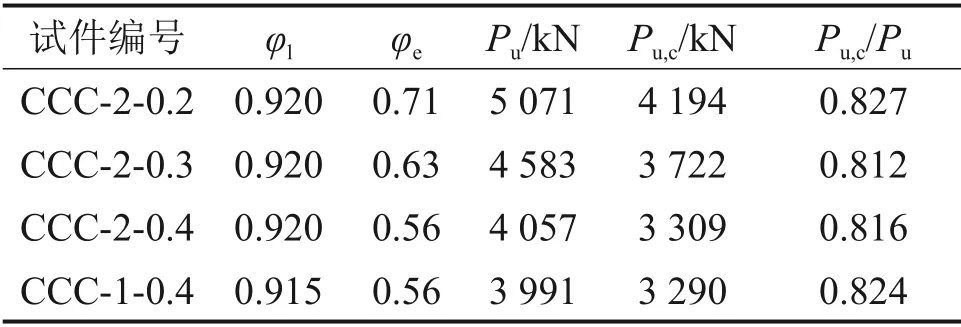
表3 公式计算结果与试验结果的对比Table 3 Comparison of calculated and test results

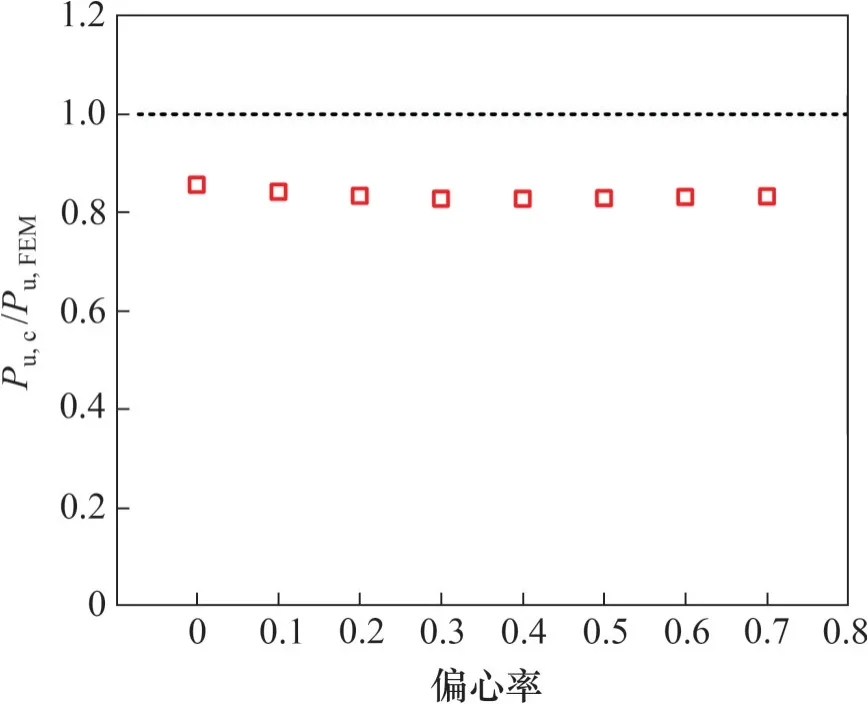
图17 公式计算结果与有限元结果的对比Fig.17 Comparison of calculated and numerical results

5 结论

1)CCC 试件在偏压荷载作用下的破坏表现为整体弯曲变形同时伴有近载侧柱肢钢管的多处局部鼓曲，近载侧柱肢能够近似发挥自身的轴心抗压强度。

2)CCC试件的轴向荷载-变形曲线特征与其对应的CFST短柱轴压曲线特征相似，即峰值荷载后荷载出现突降，但随后残余承载力能够基本维持平稳，残余承载力相对峰值荷载的下降幅度随钢管混凝土柱肢的约束系数提高而降低。

3)CCC 试件偏压承载力随着偏心率增大近似呈线性降低，偏心率从0.2增大到0.4，承载力降低20%。增加系梁数量对CCC 试件偏压承载力的提高影响并不明显。

4)建立的有限元模型能够较好地模拟CCC 试件在偏压荷载下受力行为。通过应力分析发现系梁在峰值荷载前保持弹性，其工作机制类似于斜压杆的工作机制。

5)基于钢管混凝土格构柱设计方法，考虑剪切变形的影响，建立CCC 试件的偏压承载力计算公式，理论计算值与试验值吻合较好。