考虑波长因素的提速线路捣固作业质量评价方法研究

张皓然，何越磊，李再帏，陈云峰

考虑波长因素的提速线路捣固作业质量评价方法研究

张皓然1，何越磊1，李再帏1，陈云峰2

(1. 上海工程技术大学 城市轨道交通学院，上海 201620；2. 中国铁路兰州局集团有限公司，甘肃 兰州 73000)

捣固作业质量直接关系到线路轨道服役状态，多维度研究捣固作业后轨道几何形位的变化规律是有效提升线路捣固作业效率的关键。以某160 km/h提速干线改造工程为例，提出考虑波长因素的捣固方案，针对捣固作业后的轨道几何形位的变化，分析轨道静态不平顺数据及动态不平顺数据，研究70 m弦矢高、轨道质量指数、功率谱密度、小波变换、小波能量谱等时频分布特征，确定捣固作业前后轨道不平顺波长及幅值的变化规律。研究结果表明：考虑波长因素的捣固作业方法可以有效地改善线路的长波不平顺状态，高低不平顺的改善效果优于轨向不平顺；曲线区段改善率大于直线区段且曲线轨道质量改善率随圆曲线半径的增大而降低；线路线形得到基本控制后不能通过盲目地增加捣固作业次数来达到改善轨道质量的目的。

线路提速；长波不平顺；有砟轨道；功率谱；小波变换；小波能量谱

捣固施工作业质量直接影响到线路质量，因此对捣固施工作业质量的评价也变得尤为重要。科学合理的评价方法不但能从多维度去评价捣固施工作业质量，且能够挖掘捣固施工作业中存在的问题，从而解决相应弊端，提高捣固施工作业效率，降低施工成本。捣固施工作业质量可以通过作业后的轨道不平顺指标来反映[1]，因此，可用测得的相应轨道数据为载体，挖掘数据中的有用信息，对轨道质量进行评价，从而实现对捣固施工作业质量的评价。目前，国内外对轨道质量管理都侧重于通过轨道不平顺的幅值对轨道状态进行评价，如我国的局部超限评分法和轨道质量指数(track quality index，TQI)、荷兰的Q指数、日本的P指数、美国的TQI等；并探索了轨道不平顺谱的评价方法，国内外学者对此有一些探索性的研究。赵国堂等[2]通过利用轨道不平顺时域分析、累计分布以及谱分析等方法，对高速铁路轨道不平顺谱进行拟合，以此来评价轨道区段质量。陶凯等[3]从检测项目、数据质量等方面出发，结合现场维修作业单元管理理念，提出适用于铁路正线轨道单元区段几何质量的综合量化评价方法。李再帏等[4]将轨道不平顺波长因素纳入轨道质量评价中，提出本征模函数的轨道质量评价方法。YANG等[5]提出了时频能量密度方法来分析联合空间距离−频率平面中轨道不规则性的特征。MA等[6]提出基于车体振动加速度的轨道质量评估指标。杨翠平等[7]则提出一种基于带通滤波的轨道不平顺敏感波长计权评价指标，通过考虑波长因素的加权质量指数反映实际的轨道状态。随着列车速度的增加，长波不平顺性的影响会更加明显[8]，故对有砟线路提速的捣固施工作业除了要满足一般的单纯为改善线路质量的捣固施工作业标准外，还要考虑到长波平顺性控制指标。因此对提速线路捣固施工作业质量的评价，不能仅仅局限于TQI等方法，还要考虑波长因素，目前针对从波长特性的角度去评价捣固施工作业质量的研究却相对匮乏。本文在综合现有研究基础上，结合工程实例，以轨道静态不平顺数据及动态不平顺数据为载体，通过70m弦矢高、轨道质量指数、功率谱密度、小波变换、小波能量谱等方法，挖掘数据中的信息，从不平顺波长控制角度对捣固施工作业前后的线路质量进行多维度综合评估，从而提出一套考虑长波不平顺的捣固施工作业质量评价体系。

1 考虑长波平顺性的捣固方案

本研究以某提速线路改造项目为背景，该线路为双线电气化铁路，现有运营速度为120 km/h，提速改造目标为开行动车组列车，运营速度为160 km/h，线路全长为155 km。铁路管理部门在此线路上除常规的捣固作业控制方法外，采用了70 m弦长矢距优化控制作业方法(将轨道平纵断面70 m弦矢高控制在10 mm以内)，目的是进一步控制长波不平顺，提高列车高速行驶舒适性。

该方法的主要思路是基于轨道平顺性情况确定起拨道量，采用中点矢距法，计算轨向和高低不平顺，以70 m弦长、10 mm矢高为轨道平顺性控制标准，并依据单次可调量范围对拟调整量进行约束。将不同控制条件进行整合，通过最优化算法进行求解，得到既满足约束条件又保证调整量之和最小的轨道最优调整量。

设待调整点的间距为1 m，为待调整点编号，各点的拟调整量统称为()，平纵断面偏差为()。令：()为调整后剩余偏差，则有：

1) 单次调整量限值约束：

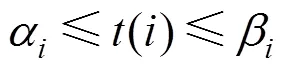
式中：α和β分别为调整点单次可调量的下限和 上限。

2) 70 m弦长波的高低和轨向的平顺性约束

式中：和分别为70 m弦的起终点位置；为弦中点位置；为高低和轨向平顺性阈值。

以弦长为基本单元，按照轨道待调整点里程顺序逐点移动弦端点，并依次求解各个基本单元内对应的调整量。随着移动弦遍历所有待调整点，使各点对应的调整后高低和轨向平顺性均满足约束要求，检测过程如图1所示。

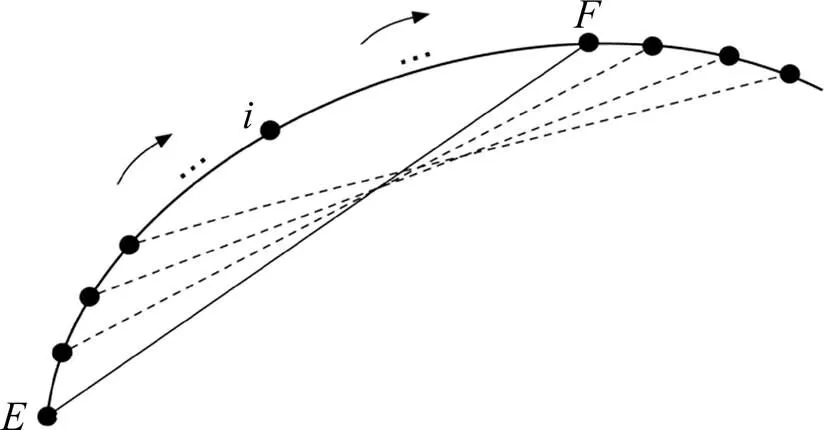
图1 70 m弦逐点移动示意图

2 时域分析

2.1 区段线路70 m弦矢高作业前后变化

大机捣固作业主要整正高低、轨向等轨道不平顺[9]，但对不同轨道不平顺指标的改善效果不尽相同[10]。为了分析捣固作业效果，本研究这里采用轨向和高低不平顺值2项指标对线路平面和纵断面平顺性进行评价。

随机抽取遍布整条线路的路段，且经过计算所选路段TQI与整条线路相近，因此所选数据具有代表性和普适性。根据频谱分析的要求[11]，分别选用3段1 km的直线和曲线路段，其中直线路段选取里程为36.310～37.333 km，94.320～95.343 km，158.273～159.296 km，标记为直线区段(1)、直线区段(2)、直线区段(3)，曲线路段选取圆曲线半径为4 000，5 000和6 000 m，对应里程为135.875～ 136.898 km，76.802～77.825 km，113.469～ 114.492 km，标记为曲线区段(1)、曲线区段(2)、曲线区段(3)，数据类型包括轨道静态不平顺数据及动态不平顺数据，时间序列标签为“一捣前”、“一捣后”、“二捣后”，每段数据采样点数为1 024个。作业前后平纵断面70 m弦长矢高变化趋势如图2所示。

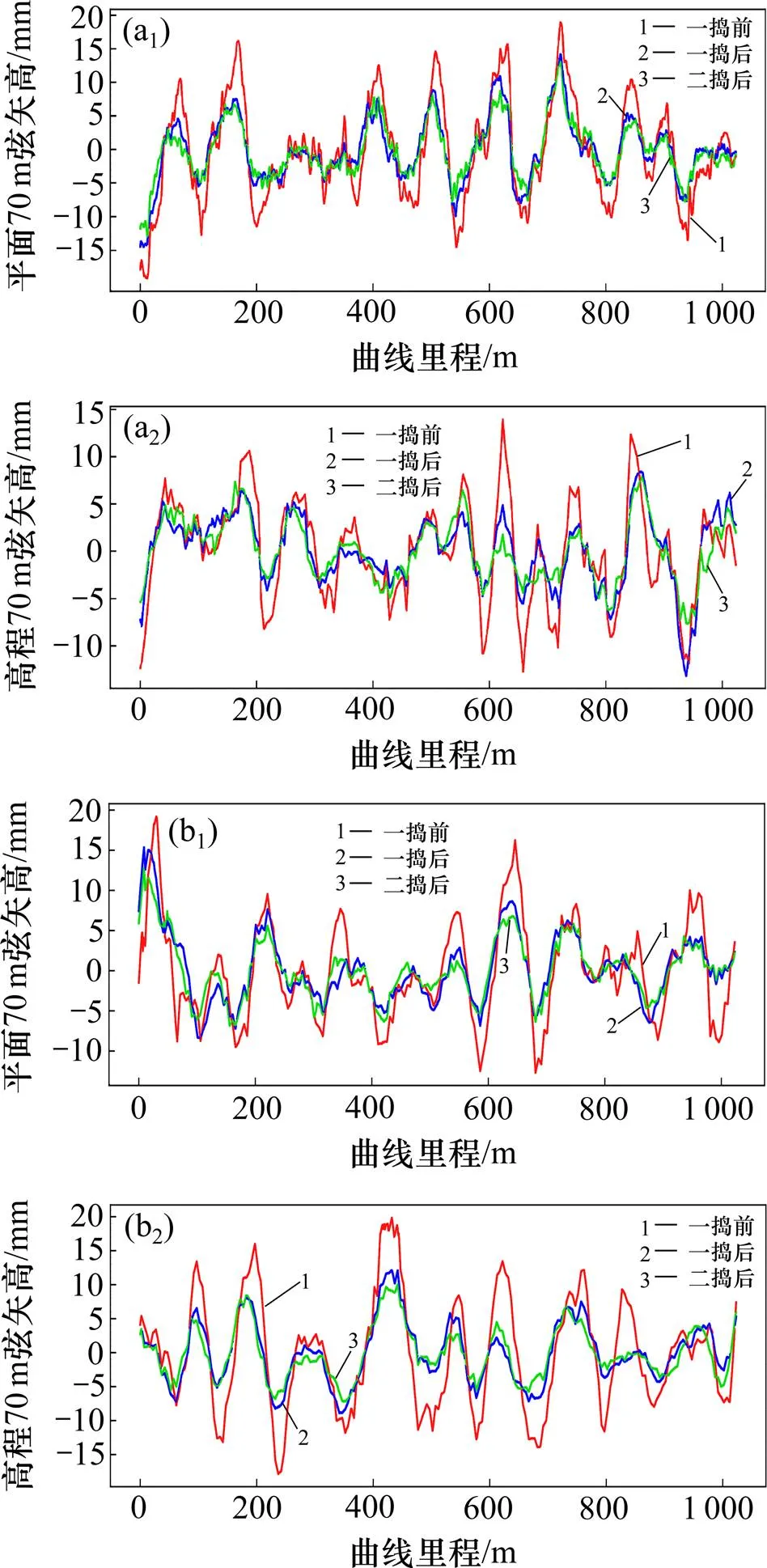
(a1), (a2) 直线区段(1)平面和高程70 m弦矢高；(b1), (b2) 曲线区段(1)平面和高程70 m弦矢高

从图2可以看出，直线和曲线区段一捣前后变化趋势明显，证明作业效果显著，而二捣前后的70 m弦矢高变化区分度相对较低，但值得注意的是，经过二捣之后的矢高均控制在了10 mm以内。此外，曲线区段的高程70 m弦矢高相对于直线优化效果较为显著。

2.2 区段轨道质量指数

一般而言，我国目前通常采用轨道质量指数(Track Quality Index，TQI)对线路状态进行管理。因此本研究这里分析了捣固前后线路的TQI变化情况。总线路TQI变化趋势如表1所示。

表1 总线路TQI变化趋势

由表1可知，总线路TQI从最初的6.95降至最终的3.32，作业改善效果明显，满足工务部门提出的最终作业后的全线TQI不超过3.4的要求。这里同样给出了作业改善率[12]，计算得出总线路一捣后和二捣后TQI的改善率分别为34.24%和27.35%，即首次作业效果相对显著。

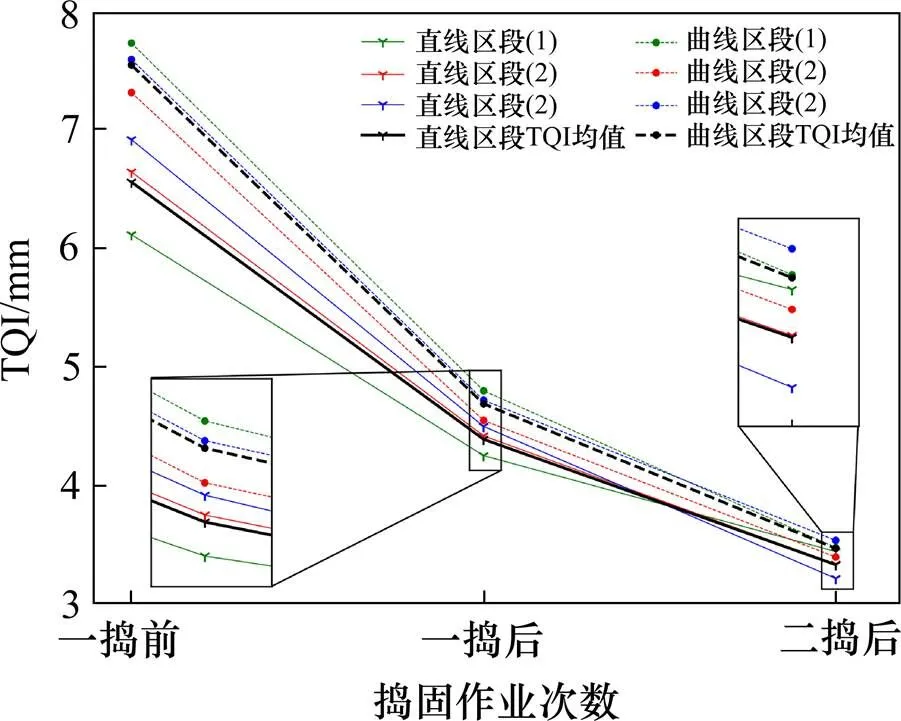
图3 区段TQI变化趋势

为了对比分析，同样给出了2.1样本的TQI分布。如图3所示，二捣后区段的TQI均分布在3.4上下，且幅值区间为[3.2,3.6]，说明TQI离散性较小；折线图整体趋势呈锥形，即每次作业后的直线区段和曲线区段TQI在明显降低的同时呈现趋同趋势；直线区段一捣后和二捣后TQI的改善率分别为33.02%和24.05%，曲线区段一捣后和二捣后TQI的改善率分别为37.81%和25.94%。此数据表明，对于曲线和直线而言，均是首次作业质量效果较优，且曲线每次的改善率均大于直线；但是TQI值也均在直线之上，这是由于曲线线路质量较差，尽管改善率要优于直线，但是线路质量仍无法达到直线区段质量程度。此外，图4给出了70 m弦与20 m弦的TQI在捣固作业前后的折线图，数据来源同上，通过对比发现，直线和曲线区段的20 m弦的TQI均大于70m弦，通过计算得出70 m弦长所对应的直线区段和曲线区段TQI的改善率分别为0.33，0.24，0.38，0.26和20 m弦长则为0.31，0.24，0.35和0.25，故采用70 m弦长策略TQI改善率较高。

图4 70 m弦长与20 m弦长TQI对比

3 功率谱评价

前述分析方法仅从时域的角度分析作业效果，无法确定现有的70 m弦捣固作业的波长控制效果，因此，本研究采用轨道谱的方法进行分析。具体的计算方法为Welch[3]，窗函数选用汉宁窗，样本同3.1。由于区段表现特征较为相似，故只各取一段进行分析，分析数据为直线区段(1)及曲线区段(1)。

图5为计算结果。图中细节放大部分表示60～80 m波长所对应频率的功率谱密度变化趋势，可以看出，轨向和高低不平顺数据长波不平顺在一捣后有比较明显的改善，说明采用70 m弦长矢距优化方法对波长控制的有效性，且二捣后的改善程度较一捣后弱，结论与之前TQI分析相同。此外对比可知，高低不平顺改善效果优于轨向不平顺。

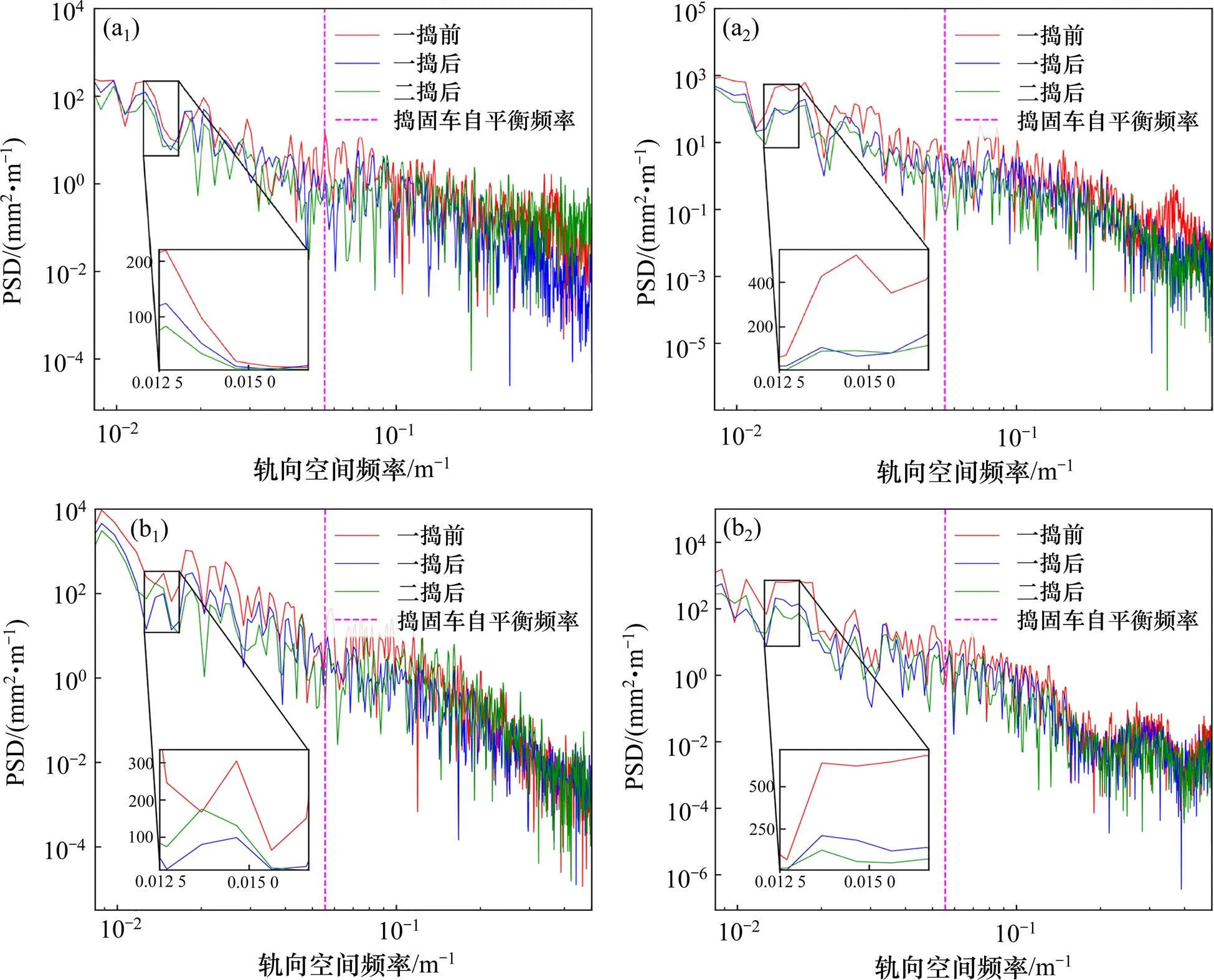
(a1), (a2) 直线区段(1)轨向和高低不平顺；(b1), (b2) 曲线线区段(1)轨向和高低不平顺

图5中竖虚线为轨检车捣固车自平衡频率值，可以看出，在竖虚线左侧，一捣前、一捣后、二捣后的PSD幅值有明显的降低趋势，而在竖虚线右侧，每次作业后的幅值区分度不强，甚至线路部分区域出现反弹现象，这是由于捣固车自平衡频率所导致，而以控制长波不平顺为主要目的的优化方案无法影响到该频率所对应波长以下的范围。另外，考虑到随着捣固次数增加，道砟颗粒集配会发生变化，同时也会改变道床的阻力[13]，由此引起的其他问题也会随之而来，所以并不能通过盲目地增加捣固次数达到不断优化线路的目的。

4 小波时频评价

4.1 小波时频分析

轨道谱方法虽然可以有效地呈现波长能量的变化，但对于相应频段的时频分布特征尚无法确定，因此，本研究采用小波分析方法进行捣固作业后轨道不平顺时频分布特性的研究，分析数据同前。根据文献[14]，采用dB4小波作为小波基函数，由于是二进制小波，轨检车采样间隔为1 m，而小波分解后第层对应波长区间大致为[s·2,s·2+1](s为采样间隔)，因此，当分解为6层时，最后一层的波长区间为[64,128]，已满足分析所需波长范围的要求，因此本文选用小波分解的层数为6层。由于捣固车作业时，对于波长控制的最大波长为18 m，因此，仅需分析18 m以上的波长即可，而小波分解对应的4~6层所对应波长范围分别为：[16,32]，[32,64]和[64,128]，这也正是本研究所分析的波长范围。

(a) 直线区段(1)轨向和高低不平顺；(b) 曲线区段(1)线轨向和高低不平顺

计算结果如图6所示，一捣后4～6层的幅值均得到了有效控制，可见优化捣固方法是有效的。而二捣后的改善效果并不明显，可见捣固车作业质量不稳定，并不是每次捣固都可以有效地控制轨道质量。小波分析重在分析相应频段的时频分布特征，从定性的角度，无法看出捣固作业对线路长波不平顺的改善效果与圆曲线半径的变化之间的联系，具体表现还需通过后面的小波能量谱变化幅值来定量分析。此外，通过小波分析，对局部优化效果不明显甚至出现反弹的路段采用局部优化策略，而不用为了控制局部线路状况对整条线路进行施工，从而节约施工成本。

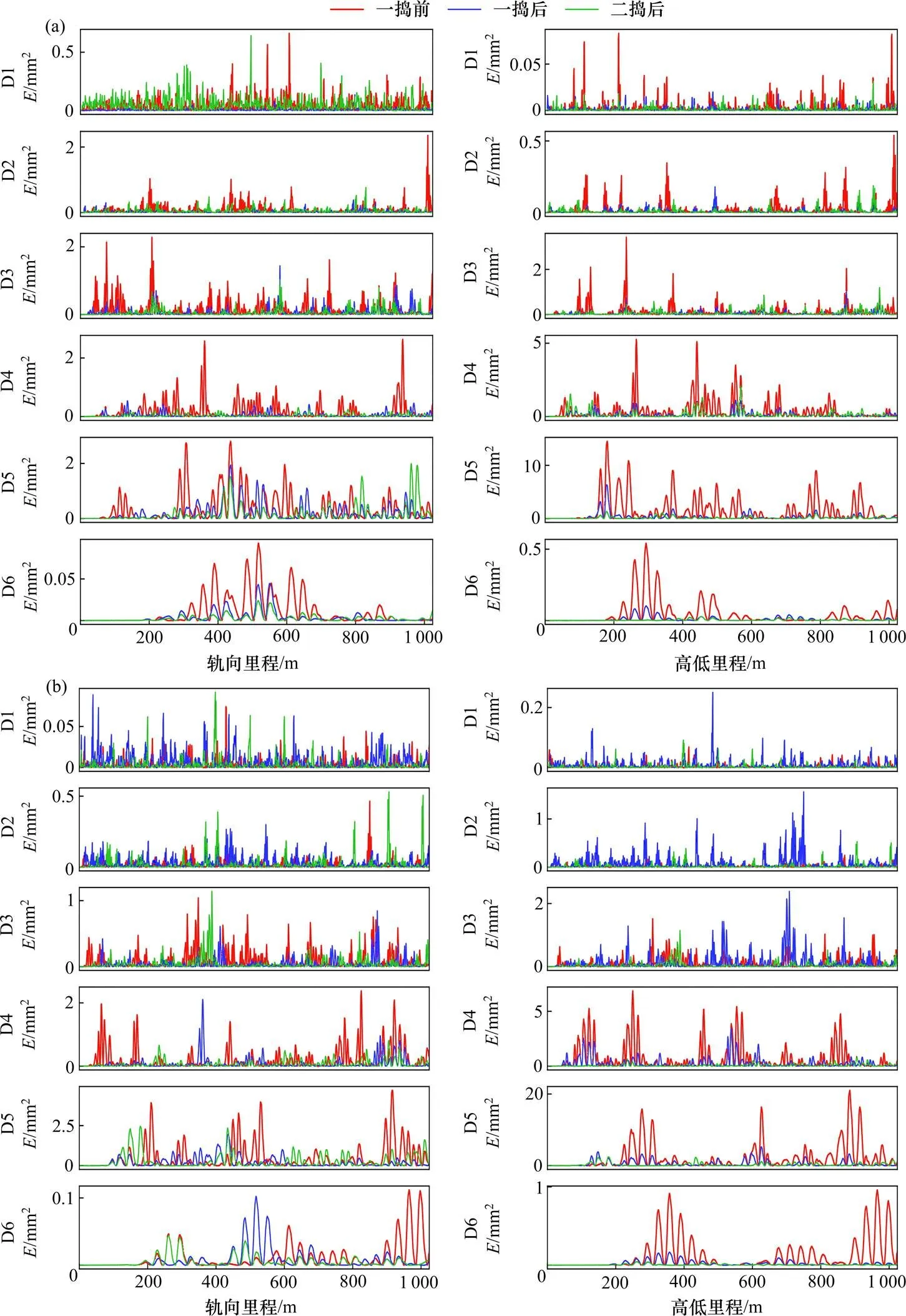
(a) 直线轨向和高低不平顺；(b) 直线轨向和高低不平顺

4.2 小波能量谱分析

为了进一步定量化轨道区段波长的能量分布状态，本研究对小波分析的能量谱进行了计算[15]。计算结果如图7所示，相对于小波分析，小波能量谱的反应更加显著，通过小波能量谱分析，可以看出能量在作业后线路质量得到优化的显著效果，由于轨道空间几何形位的调整具有联动性，当长波得到控制后，短波也得到相应控制，即第6层的波长在得到改善的基础上，第4层和第5层波长也得到相应改善。

图8采用图7中的能量值，由图可知，直线区段轨向和高低不平顺能量幅值随着捣固次数的增加均有明显降低，且高低不平顺作业后能量降低幅值大于轨向不平顺，小波能量谱按能量幅值从大到小分别为第5层，第4层，第6层，对应波长范围分别为[32,64]，[16,32]，[64,128]，另外，同前分析，呈现随着捣固次数增加，改善率降低的现象。

(a), (d) 直线区段捣固次数；(b), (e) 曲线区段捣固系数；(c), (f) 直线和曲线区段捣固次数

由直线区段折线图8(a),8(d)与曲线折线图8(b),8(e)可以看出，曲线区段能量幅值大于直线区段，这源于曲线段路况复杂，存在超高，所受车轮荷载作用较大，故线路质量恶化较为严重。其中曲线图反映出，随着曲线半径的增加，能量幅值递减的现象，说明半径愈小的区段，由于向心力的作用，在相同的行驶速度的情况下，钢轨所受轮轨侧向力作用越大，另外，为平衡纵向力，半径越小的曲线路段，所设超高越大，故原始线形破坏越严重，作业后路况改善效果越明显。

5 结论

1)验证了70 m弦长矢距优化控制作业方法的有效性。此外，以控制长波不平顺为主要目的的优化方案无法影响到该频率所对应波长以下范围。

2)高低不平顺的改善效果优于轨向不平顺，曲线区段改善率大于直线区段，其中，曲线轨道质量改善率随圆曲线半径增大而降低。

3) 在线形得到基本控制的基础上，并不能通过盲目地增加捣固作业次数来达到改善轨道质量的目的。

[1] 李仕毅, 刘仍奎, 王福田. 轨道不平顺指标与线路捣固作业质量的相关性分析[J]. 铁道建筑, 2019, 59(11): 114−118. LI Shiyi, LIU Rengkui, WANG Futian. Correlation analysis between track irregularity indexes and quality of ballast damping operation[J]. Railway Engineering, 2019, 59(11): 114−118.

[2] 赵国堂, 刘秀波, 高亮, 等. 哈大高速铁路路基冻胀区轨道不平顺特征分析[J]. 铁道学报, 2016, 38(7): 105− 109. ZHAO Guotang, LIU Xiubo, GAO Liang, et al. Characteristic analysis of track irregularity in subgrade frost heave area of Harbin-Dalian high-speed railway[J]. Journal of the China Railway Society, 2016, 38(7): 105− 109.

[3] 陶凯, 王巍, 赵志荣, 等. 轨道几何质量综合量化评价方法[J]. 铁道建筑, 2019, 59(10): 119−122. TAO Kai, WANG Wei, ZHAO Zhirong, et al. Comprehensive quantitative evaluation method of track geometry quality[J]. Railway Engineering, 2019, 59(10): 119−122.

[4] 李再帏, 练松良. 基于本征模函数的轨道质量评价方法[J]. 同济大学学报(自然科学版), 2013, 41(2): 213− 217. LI Zaiwei, LIAN Songliang. Track quality assessment method based on intrinsic mode function[J]. Journal of Tongji University (Natural Science), 2013, 41(2): 213− 217.

[5] YANG Youtao, LIU Guoxiang, WANG Xiaowen. Time-frequency characteristic analysis method for track geometry irregularities based on multivariate empirical mode decomposition and Hilbert spectral analysis[J]. Vehicle System Dynamics, 2020: 1−24.

[6] MA Shuai, GAO Liang, LIU Xiubo, et al. Deep learning for track quality evaluation of high-speed railway based on vehicle-body vibration prediction[J]. IEEE Access, 2019, 7: 185099−185107.

[7] 杨翠平, 从建力, 王源, 等. 基于带通滤波的轨道不平顺敏感波长计权评价方法[J]. 振动与冲击, 2019, 38(19): 1−6. YANG Cuiping, CONG Jianli, WANG Yuan, et al. Weighted assessment method for sensitive wavelength of track irregularity based on band pass filtering[J]. Journal of Vibration and Shock, 2019, 38(19): 1−6.

[8] 高建敏, 翟婉明, 王开云. 高速行车条件下轨道几何不平顺敏感波长研究[J]. 铁道学报, 2012, 34(7): 83−88. GAO Jianmin, ZHAI Wanming, WANG Kaiyun. Study on sensitive wavelengths of track irregularities in high-speed operation[J]. Journal of the China Railway Society, 2012, 34(7): 83−88.

[9] Khouyia, Larsson-kraik P, Nissen A, et al. Optimisation of track geometry inspection interval[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2014, 228(5): 546−556.

[10] Soleimanmeigouni I, Ahmadi A, Arasteh Khouy I, et al. Evaluation of the effect of tamping on the track geometry condition: a case study[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2018, 232(2): 408−420.

[11] 房建, 雷晓燕, 练松良, 等. 提速线路轨道不平顺不利波长的研究[J]. 铁道工程学报, 2010, 27(11): 27−31.FANG Jian, LEI Xiaoyan, LIAN Songliang, et al. Research on track irregularity and unfavorable wavelength of speed-increased railway[J]. Journal of Railway Engineering Society, 2010, 27(11): 27−31.

[12] 木东升, 周宇, 韩延彬, 等. 轨道综合作业对高速铁路有砟轨道几何不平顺改善效果[J]. 交通运输工程学报, 2018, 18(5): 90−99. MU Dongsheng, ZHOU Yu, HAN Yanbin, et al. Effect of track comprehensive maintenance on geometry irregularity improvement of ballast track in high-speed railway[J]. Journal of Traffic and Transportation Engineering, 2018, 18(5): 90−99.

[13] Aingaran S, LE PEN L, Zervos A, et al. Modelling the effects of trafficking and tamping on scaled railway ballast in triaxial tests[J]. Transportation Geotechnics, 2018, 15: 84−90.

[14] 吕宏, 李再帏, 何越磊. 考虑波长因素的轨道不平顺预测研究[J]. 铁道科学与工程学报, 2015, 12(6): 1312− 1318. LÜ Hong, LI Zaiwei, HE Yuelei. Theprediction method considering the factors of track irregularity wavelength[J]. Journal of Railway Science and Engineering, 2015, 12(6): 1312−1318.

[15] 徐磊, 陈宪麦, 徐伟昌, 等. 小波能量谱在铁路轨道检测中的应用[J]. 振动工程学报, 2014, 27(4): 605−612. XU Lei, CHEN Xianmai, XU Weichang, et al. Application of wavelet energy spectrum in railway track detection[J]. Journal of Vibration Engineering, 2014, 27(4): 605−612.

Research on quality evaluation method of ballast tamping operation for raising speed railway considering the factor of wavelength

ZHANG Haoran1, HE Yuelei1, LI Zaiwei1, CHEN Yunfeng2

(1. School of Urban Rail Transit, Shanghai University of Engineering Science, Shanghai 201620, China;2. Maintenance Department, China Railway Lanzhou Group Co., Ltd., Lanzhou 73000, China)

The quality of ballast tamping operation is directly related to the service status of the railway track. Multi-dimensional discussion of the change rule for track geometry after the ballast tamping operation is the key to effectively improving the efficiency of ballast tamping operation. This paper discussed the ballast tamping scheme considering the factor of wavelength. Starting from the changes in track geometry after ballast tamping operation, this work analyzed the static and dynamic irregularities data of track by taking a 160km/h speed-increasing trunk line reconstruction project as an example, and further studied the time-frequency distribution characteristics of the Rise of Arch of 70-meter Chord, Track Quality Index, Power Spectral Density, Wavelet Transform, and Wavelet Energy Spectrum. This paper finally determined the variation law of wavelength and amplitude about the track irregularities before and after the ballast tamping operation. The result shows that the ballast tamping operation method considering the factor of wavelength can effectively improve the long-wave irregularities state of the track. The improvement effect of the vertical irregularities is better than that of the alignment irregularities. The improvement rate of the curved section is greater than that of the straight line section. The improvement rate of curved track quality decreases with increasing the radius of circular curve. The purpose of improving track quality cannot be achieved by blindly increasing the number of ballast tamping operation after controlling the essential track linear.

raising speed railway; long-wave irregularities; ballasted track; power spectrum; wavelet transform; wavelet energy spectrum

U218

A

1672 − 7029(2021)03 − 0653 − 09

10.19713/j.cnki.43−1423/u.T20200417

2020−05−15

国家自然科学基金资助项目(51978393)；甘肃省科技计划资助项目(19ZD2FA001)

何越磊(1972−)，男，辽宁锦州人，教授，博士，从事轨道交通安全与检测技术方向研究；E−mail：hyldoc@163.com

(编辑 涂鹏)