小方坯齿轮钢连铸过程中的宏观偏析模拟

王亚栋，张立峰，张海杰

1)北京科技大学冶金与生态工程学院，北京 100083

2)燕山大学亚稳材料制备技术与科学国家重点实验室，秦皇岛 066004

宏观偏析是由于凝固前沿高溶质浓度的钢液发生相对流动而形成[1]。宏观偏析发生在1 cm～1 m的大尺度范围，在后续的轧制和均匀化热处理过程中并不能完全消除[2]，进而对产品的机械性能和稳定性产生重要影响，严重制约高端钢材的生产和应用[3].

为了改善铸坯的宏观偏析，提升铸坯及钢材的质量，众多学者通过试验和数值模拟的方法进行了大量研究[4−7]。An 等[8]通过工业试验研究发现随着结晶器电磁搅拌电流的增加，铸坯中心偏析得到改善；随着结晶器电磁搅拌频率的增加，铸坯中心偏析同样得到改善。Li 等[9]通过对比结晶器电磁搅拌、结晶器＋末端电磁搅拌（复合电磁搅拌）条件下低倍结果和铸坯中心碳偏析结果，表明复合电磁搅拌模式得到的铸坯中心疏松和缩孔更小、更均匀，能够有效改善铸坯中心碳偏析。Bleck等[10]通过实验室试验研究了轻压下区间内不同中心固相率与中心偏析和内部裂纹的关系，结果显示在中心固相率为0.89～0.94 的区间内进行压下试验，能够改善铸坯中心偏析，但是铸坯内部裂纹发生率增加。王文培等[11]进行小方坯高碳钢的工业试验，结果表明随着钢液过热度的升高，碳偏析指数增大，控制钢水过热度在30 ℃以内可保证碳偏析指数在1.10 内。Jiang 等[12]建立了二维的多相凝固模型并与机械压下模型耦合，分别研究不同压下量、压下区间等对液相流动和溶质传输的影响。研究结果显示，机械压下能够挤压铸坯芯部钢液，减缓溶质富集液相向凝固终点的流动速度，有效降低铸坯中心偏析。随着压下量的增加，中心偏析明显改善；提出最佳的压下区间为中心液相率在0.95～0.01 之间。Wu 和Ludwig[13]利用多相凝固模型研究了钢锭凝固过程中的溶质传输行为，研究表明宏观偏析仅在熔体对流或者枝晶沉降过程中形成。Sun 和Zhang[14]建立了电磁搅拌、传热和溶质传输的耦合模型并预测了连铸坯的宏观偏析，模拟结果与实验室检测结果吻合较好。马长文[15]利用连续介质模型，研究了钢锭侧面和底面冷却条件下的偏析行为，侧面冷却时在铸锭顶部形成正偏析，底部形成负偏析；底部冷却时铸锭内部产生垂直生长的通道偏析。陈华标[16]针对板坯连铸过程建立了全连铸三维中心偏析模型，并模拟研究了连铸凝固过程中板坯内溶质的分布特征及中心偏析的形成机理.

由于连铸过程为高温作业，各种传输过程复杂，难以直接观察且试验过程耗费较多的人力和物力，越来越多的研究者采用数值模拟的方法研究连铸凝固过程。然而，在连铸的数值模拟中，由于连铸模型庞大、计算量较大、计算时间较长，很难及时反馈模拟结果。本文基于ProCAST 软件建立简化的移动切片模型，能够高效模拟连铸过程中的宏观偏析，研究了不同过热度、二冷水量和拉坯速度等对宏观偏析的影响规律.

1 数学模型

本研究基于国内某钢厂小方坯齿轮钢连铸生产，利用ProCAST 软件建立移动切片模型，模拟连铸坯的宏观偏析。由于实际连铸过程较为复杂，为了简化模型以提高计算效率做出如下假设：连铸坯沿拉坯方向的导热量约占总热量的3%～6%，因此忽略连铸坯纵向传热[17]；连铸二冷区同一段采用均匀冷却的经验公式[18]；凝固过程未考虑枝晶沉降和固相移动[19]；未考虑实际生产中电磁搅拌的影响。模型中偏析的计算主要由连续性方程、动量方程、能量方程和溶质传输方程控制,方程（1）、（2）和（3）分别为连续性方程、动量方程和能量方程，方程（4）和（5）分别为液相和固相中的溶质传输方程.

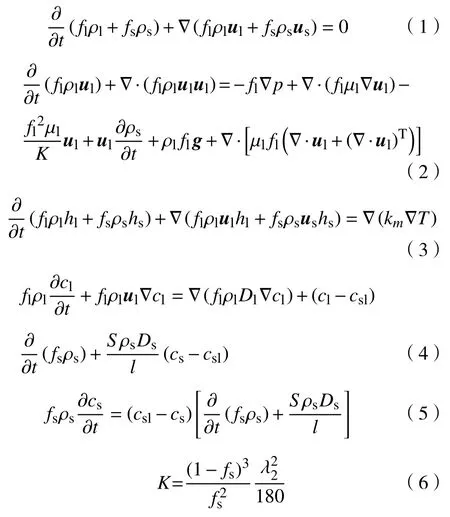
式中，fl(fs)为液（固）相率；ρl(ρs)为液（固）相密度，kg·m−3；t为时间，s；ul(us)为液（固）相速度，m·s−1；μl为液相黏度，Pa·s；K为渗透率，m2；g为重力加速度，m·s−2；p为压力，Pa；hl(hs)为液（固）相焓，J·mol−1；Dl(Ds)为液（固）相扩散系数，m2·s−1；T为节点温度，℃；km为热导率，W·m−1·K−1；cl(cs)为实际的液（固）相浓度；csl为界面浓度；λ2为二次枝晶间距，m；l，S为常数.

小方坯齿轮钢断面尺寸为165 mm×165 mm，拉坯速度为1.4 m·min−1，连铸机弧型段半径为10 m，结晶器有效长度为0.85 m。齿轮钢成分如表1 所示，钢种的固液相线温度分别为1463 ℃和1514 ℃.图1 为本研究建立的移动切片模型示意图。通过ProE建立切片模型，模型边长和厚度分别为165 mm 和10 mm，采用6 面体网格，体网格总数为15125 个.移动切片从弯月面开始，按照图1 所示连铸坯移动示意图进行运动，分别经历结晶器冷却、二冷区冷却和空冷区，最终完全凝固。连铸各区长度和冷却水量如表2 所示。为了将重力对偏析的影响加入模型，本模型将连铸弧形段不同位置处的重力加速度分别沿径向和切向进行分解，进而加载至偏析模型[12,20]，如图1 所示.

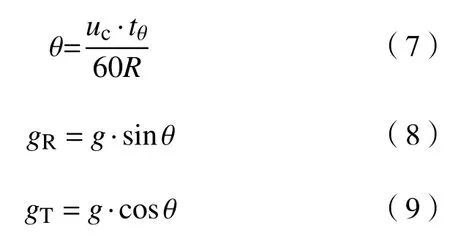
表 1 齿轮钢成分（质量分数）Table 1 Element content of the gear steel %

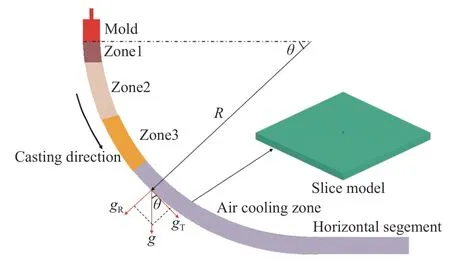
图 1 移动切片模型Fig.1 Moving slice model

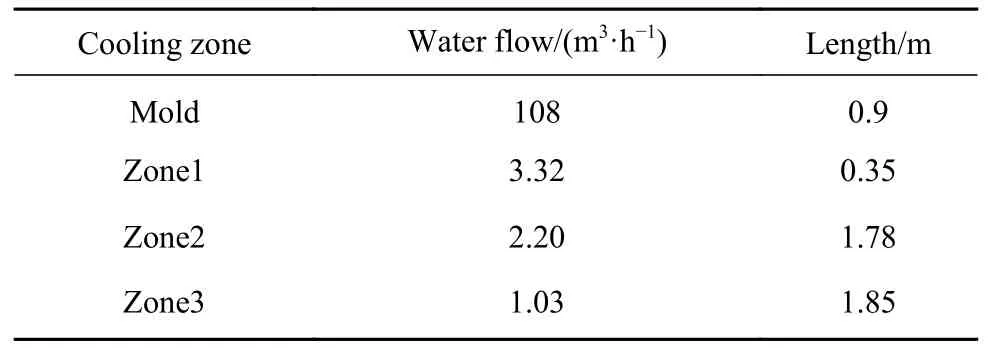
表 2 各区长度和冷却水量Table 2 Length and cooling water flow in each zone

式中：θ为连铸坯弧形段不同位置处径向与水平方向的夹角；uc为拉坯速度，m·min−1；tθ为弧形段开始至弧形段任意位置的时间，s；R为连铸机半径，m；gR为重力加速度径向分量，m·s−2；gT为重力加速度切向分量，m·s−2.

连铸生产过程中，铸坯表面与结晶器铜板接触，通过铜板内的冷却水将热量导出，在二冷区主要利用喷嘴向铸坯表面喷水（水雾）的方式冷却.在空冷区主要由铸坯表面向周围辐射散失热量.因此，需将上述传热边界条件分开处理。结晶器铜板与铸坯表面的热流密度采用平均热流密度[21]：

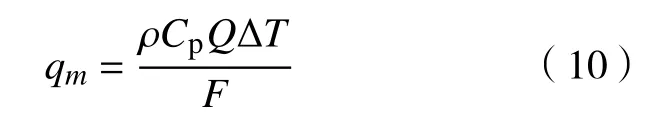
式中，qm为铸坯表面的平均热流密度，W·m−2；ρ为结晶器冷却水密度，kg·m−3；Cp为冷却水的比热容，J·kg−1·℃−1；Q为冷却水流量，m3·s−1；ΔT为结晶器铜板进出水温度差，℃；F为结晶器铜板与铸坯的有效接触面积，m2.

二冷区冷却方式主要包括喷嘴冷却、辊子与铸坯间的接触传热、二冷水聚集蒸发散热和辐射散热等，本研究采用经验公式进行计算[22]：

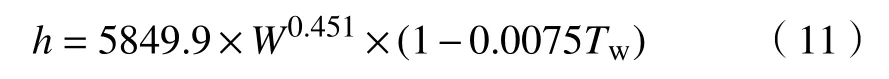
式中，h为综合换热系数，W·m−2·℃−1；W为二冷各区的平均水流密度，L·cm−2·min−1；Tw为冷却水的温度，℃.

空冷区主要通过铸坯表面与周围环境的辐射换热散失热量，采用公式（12）进行计算[18,23].

式中，qrad为铸坯表面辐射换热的热流密度，W·m−2；σ为Stefan-Boltzmann 常数，取值为5.67×10−8W·m−2·K−4；ε为辐射换热系数，取值为0.8；Ts、Te分别为铸坯表面温度和环境温度，℃。模型中齿轮钢的热物性参数通过ProCAST 软件自带的热力学数据库计算得出，钢种的热导率、密度、热焓、黏度和固相率随温度的关系如图2 所示.

2 模型验证

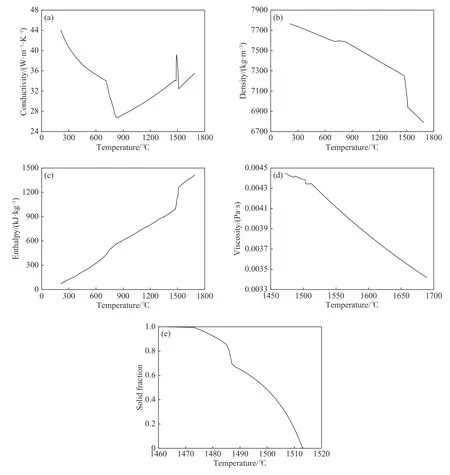
图 2 钢的热物性参数。（a）热导率；（b）密度；（c）热焓；（d）黏度；（e）固相率Fig.2 Thermophysical parameters of the steel:(a)conductivity; (b)density; (c)enthalpy; (d)viscosity; (e)solid fraction

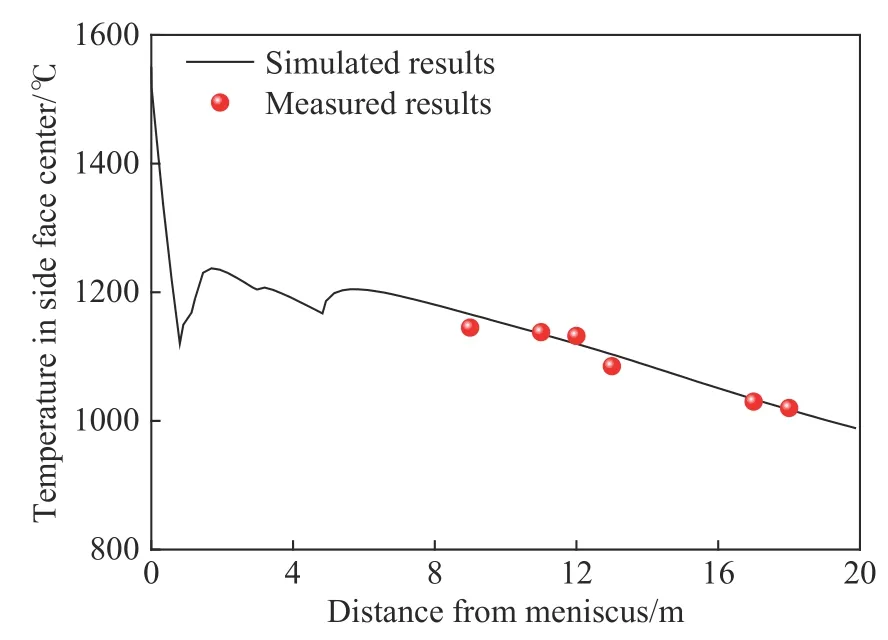
图 3 计算得到的铸坯表面温度和测量结果的对比Fig.3 Comparison between the calculated and measured results of the billet surface temperature

为了验证移动切片模型的准确性，本文基于连铸实际工况进行模拟并与检测结果进行对比.实际连铸条件如下：拉速1.4 m·min−1，过热度35 ℃，二冷水量为正常水量，如表2 所示。图3 为铸坯表面红外测温与模型计算得到的温度场对比结果，可以看出计算得到的温度场与现场测温结果基本吻合，进而验证了模型温度场的准确性。为了进一步验证宏观偏析模型的准确性，需要检测铸坯横断面的宏观偏析情况。铸坯宏观偏析检测方法为：首先进行铸坯横断面低倍浸蚀，从浸蚀后的横断面找到铸坯的凝固末端位置，过凝固末端位置从内弧至外弧做垂线，并用直径为6 mm 的钻头沿着垂线进行钻屑取样，最后利用碳硫分析仪（Leco CS844）检测碳元素含量。该检测方法的优势是能够准确定位凝固末端位置，进而得到更准确的中心偏析结果。图4 为碳偏析检测结果与模拟结果的对比，可以看出计算得到的碳偏析度与检测结果基本吻合，进而验证了模型计算宏观偏析的准确性。碳偏析度通过公式（13）计算，其中，ri为检测位置i处的碳偏析度，mi为检测位置i处的碳含量，m0为钢液中碳的初始含量.

图 4 检测得到的碳含量与模拟结果对比Fig.4 Comparison between the calculated and measured results of the carbon content

检测结果显示，铸坯表层为负偏析，这是由于结晶器电磁搅拌导致钢液冲刷凝固前沿，将凝固前沿的富集溶质带至中间钢液，进而导致铸坯表层的负偏析。随着连铸凝固的进行，碳含量逐渐增加，在距铸坯表面1/4 处出现较严重的正偏析，如图4 所示，该位置与连铸坯柱状晶向等轴晶的转变位置相吻合，此位置的正偏析主要是由于枝晶转变导致[24−25]，枝晶转变处枝晶变得更加粗大且交错排布，阻碍了选分结晶产生的溶质进一步流动，进而在枝晶转变处产生正偏析。随后碳含量逐渐降低，在凝固中心附近出现负偏析，在凝固中心处为严重的正偏析，碳偏析度可达1.16，这主要是因为在凝固末端，钢液凝固收缩形成的负压抽吸附近高浓度溶质钢液，导致严重的中心偏析和凝固中心附近的负偏析。模拟结果显示，铸坯中心附近的负偏析偏离凝固中心较远，这是因为模型未考虑凝固收缩导致。内弧侧的溶质浓度整体高于外弧侧，这主要是因为溶质浮力引起的热对流导致高溶质浓度钢液向内弧侧流动导致.

3 模拟结果

为了研究不同连铸参数对铸坯宏观偏析的影响规律，本研究分别模拟了不同过热度、二冷水量和拉坯速度条件下的宏观偏析。钢中同时存在C、Si、Mn、P、S、Cr 等易偏析元素，连铸凝固过程中易偏析元素均存在不同程度的偏析现象，易偏析元素的偏析规律基本一致[25−27]，因此，为表征铸坯的宏观偏析程度，本文选用碳偏析度作为铸坯偏析程度的标准.

拉速1.4 m·min−1，正常二冷水量条件下，本文分别模拟了过热度15、25 和35 ℃工况铸坯横断面的宏观偏析情况。图5 为铸坯横断面碳元素的分布云图，图6 为铸坯横断面中垂线上碳元素宏观偏析的定量结果。可以看出，随着过热度的增加，枝晶转变处正偏析有所增加，铸坯中心偏析明显增强，铸坯中心碳偏析度从1.06 增加至1.15。中心偏析的增强主要是因为在相同冷却条件下提高浇铸温度，铸坯凝固时间延长，溶质元素有更长的时间扩散，使得更多的溶质元素扩散至后期凝固的钢液，进而加剧了铸坯的中心偏析。可以看出，过热度在不超过25 ℃时，铸坯中心偏析和枝晶转变处偏析可以控制在一个比较低的水平。因此，将过热度控制在25 ℃以内，可以保证铸坯的宏观碳偏析度控制在1.10 范围内.

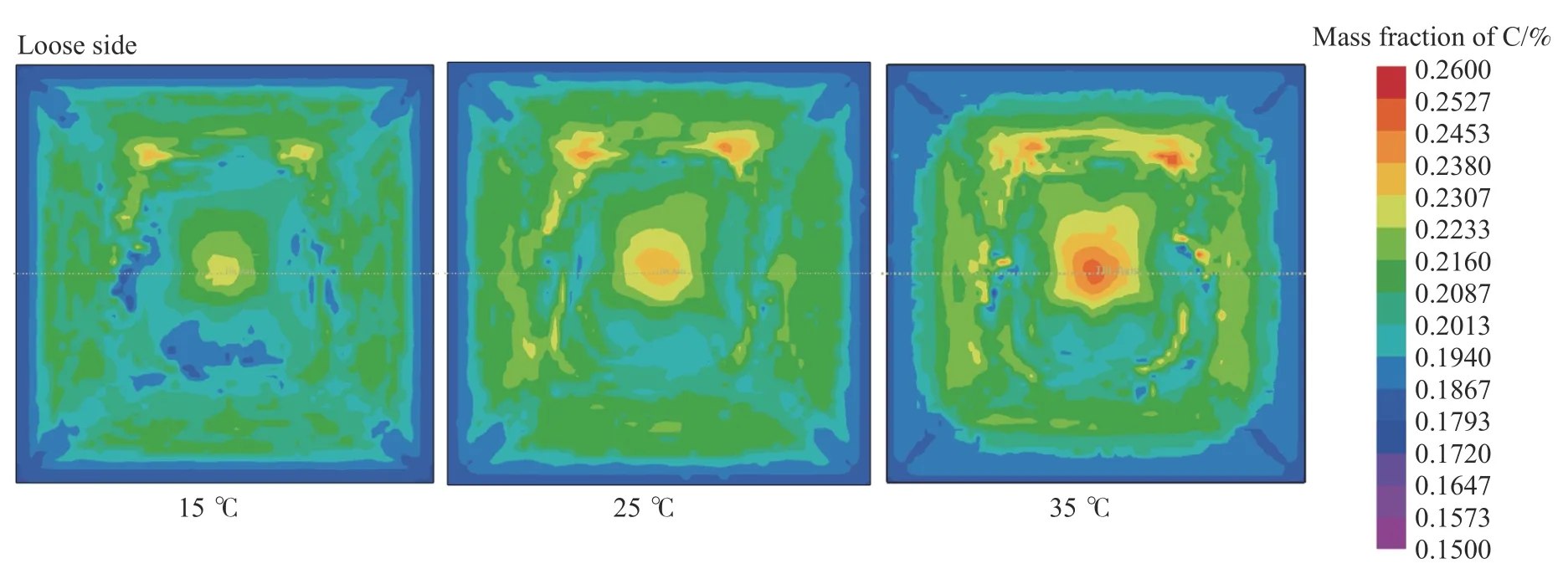
图 5 过热度对铸坯宏观偏析的影响Fig.5 Effect of superheat on the macrosegregation of the billet

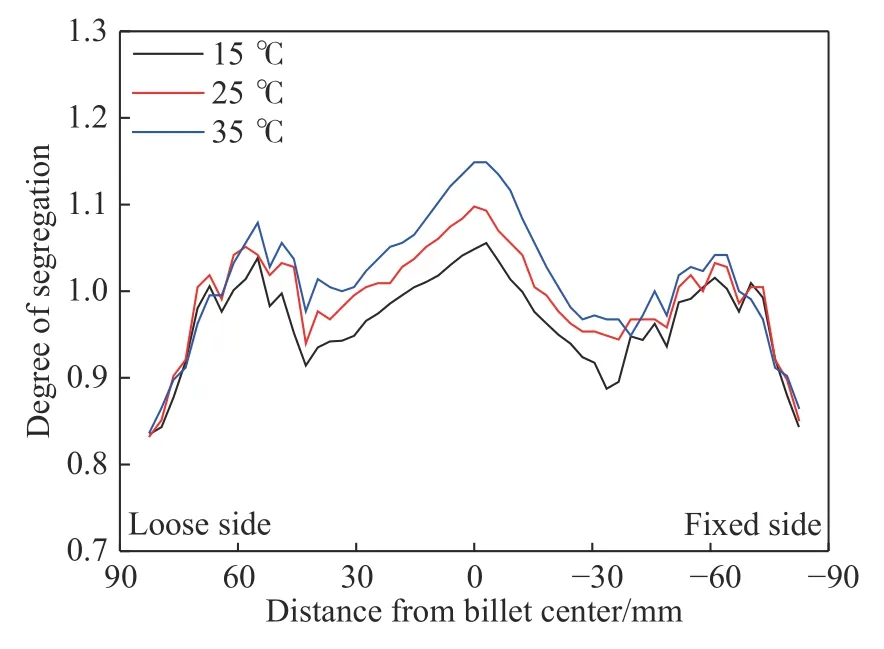
图 6 过热度对铸坯宏观偏析的定量影响Fig.6 Effect of superheat on the quantized results of the macrosegregation

模拟结果显示，铸坯内弧侧的偏析程度要强于铸坯的外弧侧。这是由于连铸过程中，当铸坯切片运动至弧形段以及水平段后，重力方向将不再垂直于铸坯横断面，进而产生平行于铸坯横断面的重力分量，钢液受到溶质浮力的影响而产生对流，溶质元素富集的钢液会向内弧侧流动，进而导致内弧侧的宏观偏析强于外弧侧.

为研究连铸二冷水量对铸坯横断面宏观偏析的影响，在拉速为1.4 m·min−1，过热度为35 ℃的条件下，本模拟分别计算了二冷水量降低20%、正常水量、二冷水量增加20%三种工况下铸坯的宏观偏析。图7 为铸坯横断面碳元素的分布云图，图8 为铸坯横断面中垂线上碳元素宏观偏析的定量结果。可以看出，连铸二冷水量对铸坯中心偏析和枝晶转变处偏析影响较小，且影响规律不明显.随着连铸二冷水量的增加，铸坯中心偏析有所改善，但是改善程度很小，铸坯中心碳偏析度从1.16 降低至1.13。这主要是因为在凝固中后期，凝固坯壳较厚，二冷水量的改变对铸坯芯部的冷却条件影响较小，即对凝固后期钢液的凝固时间影响较小，溶质扩散时间改变有限，进而对铸坯中心偏析影响较小.

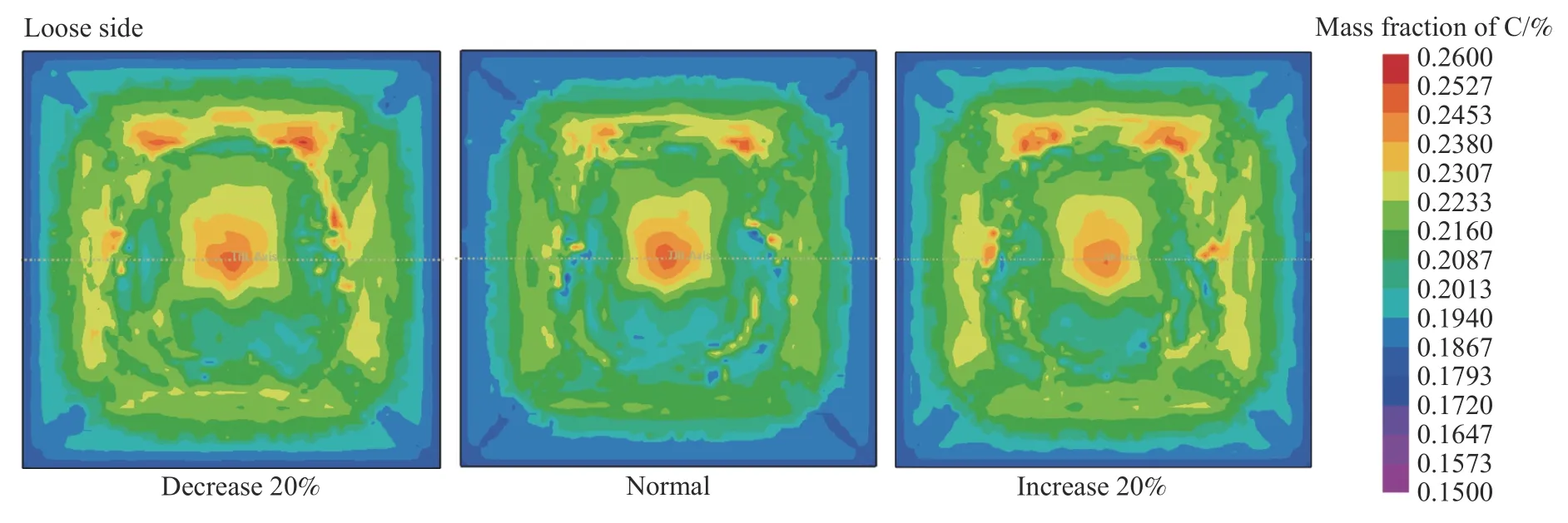
图 7 二冷水量对铸坯宏观偏析的影响Fig.7 Effect of secondary cooling water flow on macrosegregation of the billet

图 8 二冷水量对铸坯宏观偏析的定量影响Fig.8 Effect of secondary cooling water flow on the quantized results of macrosegregation

为研究拉坯速度对铸坯横断面宏观偏析的影响，在过热度为35 ℃，正常二冷水量条件下，本模型分别计算了1.2、1.4 和1.6 m·min−1三种拉速条件下的宏观偏析。图9 为铸坯横断面碳元素的分布云图，图10 为铸坯横断面中垂线上碳元素宏观偏析的定量结果。可以看出，拉速的变化对铸坯中心偏析的影响较为显著，随着拉坯速度的增加，铸坯中心偏析呈现加重的趋势，铸坯中心碳偏析度由1.14 增加至1.21。主要是因为随着拉坯速度的提高，连铸坯在结晶器区和二冷区停留时间变短，使得凝固末端向后移动，图11 显示拉坯速度在1.2、1.4 和1.6 m·min−1时，凝固末端位置距离弯月面分别为9.6、11.7 和13.9 m。进而溶质元素有更长的扩散时间，使得更多的溶质元素扩散到后期凝固的钢液中，加剧了铸坯的中心偏析.

4 结论

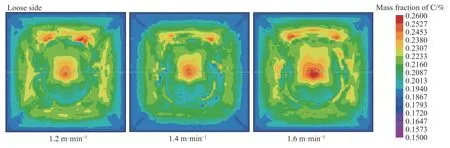
图 9 拉坯速度对铸坯宏观偏析的影响Fig.9 Effect of casting speed on macrosegregation of the billet

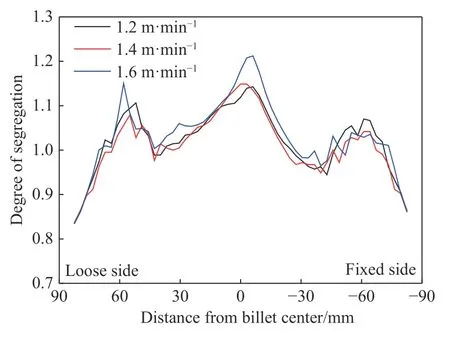
图 10 拉坯速度对铸坯宏观偏析的定量影响Fig.10 Effect of casting speed on the quantized results of macrosegregation

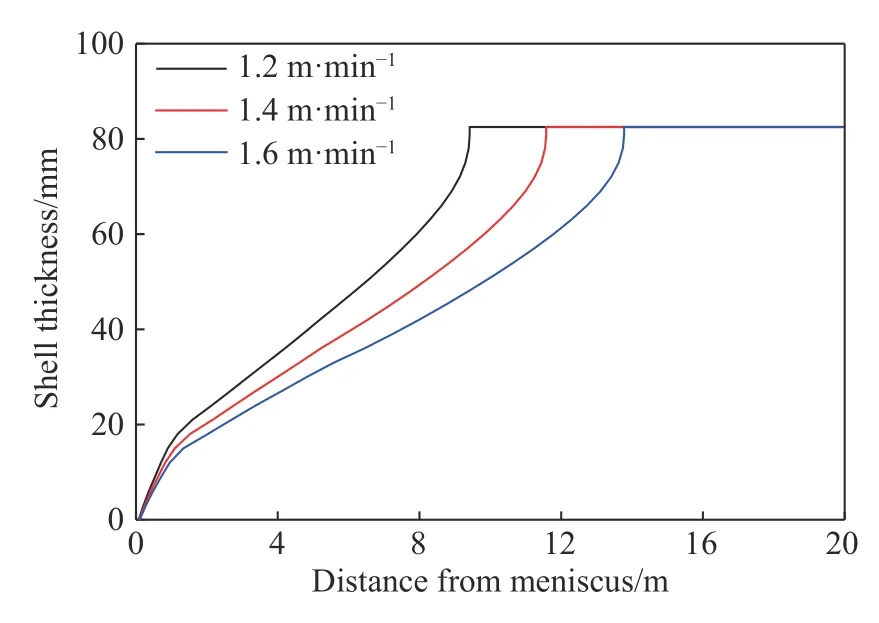
图 11 拉坯速度对凝固坯壳厚度的影响Fig.11 Effect of casting speed on the shell thickness of the billet

本文建立了连铸移动切片模型，能够高效模拟连铸过程中的宏观偏析并及时反馈模拟结果.红外测温和碳偏析检测结果与模拟结果吻合良好，验证了移动切片模型模拟连铸坯宏观偏析的准确性。模型分别模拟研究了不同过热度、二冷水量和拉坯速度对铸坯宏观偏析的影响，得出如下结论：

（1）由于钢液受到溶质浮力的影响，溶质元素富集的钢液会向内弧侧流动，导致内弧侧的宏观偏析强于外弧侧.

（2）随着过热度的增加，枝晶转变处正偏析有所增加，铸坯中心偏析明显增强，铸坯中心碳偏析度从1.06 增加至1.15。过热度控制在25 ℃范围内，可以保证铸坯的宏观碳偏析度控制在1.10 范围内.

（3）随着连铸二冷水量的增加，铸坯中心偏析改善程度较小，铸坯中心碳偏析度从1.16 降低至1.13.

（4）随着拉坯速度的增加，铸坯中心偏析呈现加重的趋势，铸坯中心碳偏析度由1.14 增加至1.21。拉速控制在1.4 m·min−1范围内，可保证铸坯中心碳偏析度低于1.15.