大面积荷载下非饱和软土场地考虑时间效应的单桩负摩阻力计算方法

薛 祥， 朱春杰， 郑 毅， 陈源浩， 侯东利， 杨素春， 周宏磊

(北京市勘察设计研究院有限公司， 北京 100038)

0 引言

近年来国内外各建设行业高速发展，各种高标准园区(如迪士尼、环球影城、世园会、园博园及各种旅游小镇等等)及机场跑道、高速公路和铁路路基、土坝场地形成等设计和施工都可能涉及到大面积非饱和软土场地填方后的桩基工程。对于这种大面积荷载下单桩负摩阻力，采用《建筑桩基技术规范》(JGJ 94—2008)[1](简称桩基规范)进行计算时，会遇到桩侧非软弱土层确定困难、基桩负摩阻力分布形式可能与该规范建议方法确定的形式有差异等问题，从而导致基桩负摩阻力估算及桩基设计困难。

关于桩基负摩阻力的研究主要有如下三个方法：现场实测、室内试验(模型试验)、理论公式及半经验半理论公式，并且研究者往往将上述各种方法结合在一起考虑，以便得到更合理的计算方法。1969年，Endo等[2]的日本东京大面积回填土堆载作用下的现场测试研究表明，桩侧负摩阻力随土的固结速率减小而不断减小、随时间呈非线性发展，直至趋于稳定。邓会元[3]进行了大面积堆载下三根工程试桩平衡堆载试验，实测结果表明，负摩阻力的发展是随时间而变化的，但未给出负摩阻力随时间变化的计算方法。1965年，Johanessen等[4]首次提出了应用有效应力原理计算桩基负摩阻力的方法，后来杨维好[5]、魏鉴栋等[6]对有效应力法和基于有效应力法的其他派生方法进行了完善和改进；关于负摩阻力的中性点位置，Elmasry[7]和Broms[8]提出了一些经验计算公式。为了考虑挤土桩的挤密效应、承台的卸载作用以及群桩的屏蔽作用，刘明振[9]基于有效应力法提出了负摩阻力作用下群桩的沉降和承载力的计算方法，但此方法需得到实际工程的验证且需对主要参数进行进一步深入研究后才能应用。

就工程实践来看，我国桩基规范、美国规范和日本规范都建议桩基负摩阻力值和中性点位置采用有效应力法计算[10]，但都为经验方法。有效应力法基于土体内的抗剪强度，把桩土间的摩阻力归因于作用在土体的有效应力。工程实践上，按有效应力法计算的负侧摩阻力在桩顶处为零，但同样是土对桩的摩擦力、同样是桩-土相对位移最大处，正侧摩阻力取土层极限侧摩阻力，而负极限侧摩阻力却为零，与正侧摩阻力取值方法相悖。此外，负侧摩阻力随桩身逐渐增大到正极限侧摩阻力时人为取值为正极限侧摩阻力，理论上需进一步研究。2014年，康景文等[11]依托实际工程现场监测资料，分析了厚填土场地的桩基负侧摩阻力的分布规律，参考桩基规范提出了负侧摩阻力系数计算方法和简化的负侧摩阻力沿轴向线性分布理论计算图，该方法仅适用于单层填土内负摩阻力估算，同时也无法估算因填土荷载对其下部土层产生的负摩阻力。

近年来传递函数法(荷载传递法)的研究较多，其基本方法是把桩划分成许多弹性单元，用非线性弹簧来联系每一桩单元与土体。佐藤悟[12]通过假定土的位移沿竖向线性变化、传递函数为理想的弹塑性，从而求得问题的解析解。周国林[13-14]考虑时间因素对传递函数法的解析求解方法做了进一步改进。但是该方法的假设条件与工程实际情况有较大的不符，在工程实践应用中有诸多的不便。

本文结合工程实践，研究总结大面积荷载作用下非饱和软土内基桩负侧摩阻力的分布规律及考虑时间效应的负摩阻力计算方法。

1 单桩负侧摩阻力分布概念模型

1.1 单桩负侧摩阻力的受力机理

根据对基桩负摩阻力总结研究及某工程大面积压实填土作用于桩侧土导致后期基桩产生负摩阻力的实践，大面积压实填土荷载作用下非饱和软弱土基桩负摩阻力产生作用机理可概化为如图1所示的受力模型。

图1 大面积压实填土荷载下基桩负摩阻力受力概念模型

以某工程场地形成、成桩等施工过程为例，对应相对变形发生、发展及稳定过程，对基桩负摩阻力的发生、发展及稳定等过程进行分析如下：工程施工对场区原地表人工填土(1～2m)进行挖除后，进行分层换填，压实大面积填土，新近沉积土层因挖除卸荷先回弹(根据监测，回弹量约3～6mm)后压缩。随着填筑厚度(荷载)的增加至完成，压缩变形逐渐增大，土层压密、固结作用持续至稳定。在这个过程中，不同的成桩时间，基桩的负摩阻力大小不同。如对场地形成后立即成桩，则上部结构施工较慢，忽略压实填土层本身的变形，假定桩侧土为弹簧体系，对其负摩阻力发生、发展及受力分析如图1所示，图中Esi，qi为桩侧第i层土压缩模量及负(或正)侧摩阻力，E为桩端下土层的压缩模量，Sc，Sp分别为桩侧土和基桩总沉降。

场地填筑完成后成桩，基桩未施加上部结构，桩顶荷载为零，基桩沉降为零，此时桩侧土压密、固结变形产生的负侧摩阻力全部作用于基桩全长，基桩除受自重荷载外，还承受上部土层向下变形产生的负摩阻力(下拽力)，随桩侧土固结变形的增大，基桩轴力(下拽力)逐渐增大，使得基桩桩端下沉，桩端处(或桩土正相对位移最先出现的点)桩侧土层开始提供向上正侧摩阻力，阻止基桩下沉。随着桩侧土压密、固结变形的增加，靠近桩端处的正侧摩阻力从零逐渐增大到极限，桩端至中性点范围土层的正侧摩阻力逐渐发挥，以平衡上部土层施加于基桩的负摩阻力。如果无外荷载，桩-土相对位移将在某一时段处于平衡状态。若上部结构(承台、建筑等)荷载继续施加，基桩在荷载作用下下沉，此时中性点以上桩侧土产生的负摩阻力、上部荷载及中性点下桩侧土产生的正摩阻力及桩端阻力处于动态平衡，直到中性点稳定在某一深度处，或直至中性点深度为零。

1.2 实测大面积荷载作用基桩负摩阻力分布规律

根据国内外部分大面积荷载作用下基桩负摩阻力实测成果[15-16]的对比分析及研究总结，大面积荷载作用下基桩负摩阻力分布的基本规律如下：1)桩侧土负侧摩阻力与桩侧土土性有关，土颗粒越粗、越硬、越密实，负侧摩阻力越大，同一土层基桩负侧摩阻力变化不大；2)在中性点以上一小段区间内，桩-土相对位移较小，基桩侧负摩阻力发挥不充分，除此外，基桩负侧摩阻力沿中性点以上范围均发挥至极限；3)从桩顶正负侧摩阻力较大、发挥较充分的实测数据来看，负侧摩阻力大小及发挥程度的最大限度与桩-土相对位移和土性相关，这与桩侧土提供正摩阻力的机理是一致的。

1.3 基桩负摩阻力数值分析

为进一步研究桩基施工完成后，桩顶无外加荷载条件下，随着桩侧土压密、固结变形的增加，桩身范围内侧摩阻力的分布和变化规律。本文在搜集实际地层和沉降监测资料的基础上，利用PLAXIS软件及传递函数模型，采用有限元弹塑性固结分析方法进行场地形成、桩基施工等分阶段全过程的施工模拟。本次数值分析中，各层非软土体的初始参数取值按照地质勘察报告中的土工试验、现场测试的指标以及北京地区经验确定，土体本构关系采用摩尔-库伦模型。并利用场地实时的现场沉降监测资料(限于篇幅未给出)，对桩侧土及大面积压实填土的模型参数进行了反演分析及校正。模拟分析发现，桩顶荷载为零的条件下，随着桩侧土的压密、固结变形的增大，基桩轴力逐渐增大，桩侧摩阻力从零(正侧摩阻力、负侧摩阻力)逐渐增大，中性点向下移动，某一时间点后中性点处于稳定状态，桩侧摩阻力不再变化。在桩侧土压密、固结向下变形过程中，负侧摩阻力根据桩-土相对位移大小沿桩顶至中性点逐渐发挥，桩侧土逐渐向基桩施加向下的负摩阻力(下拽力)，最终达到极限状态。在中性点向上的一小段区间内，由于桩-土相对位移较小，负侧摩阻力尚未发挥至极限。桩身最终的负摩阻力分布情况如图2所示。

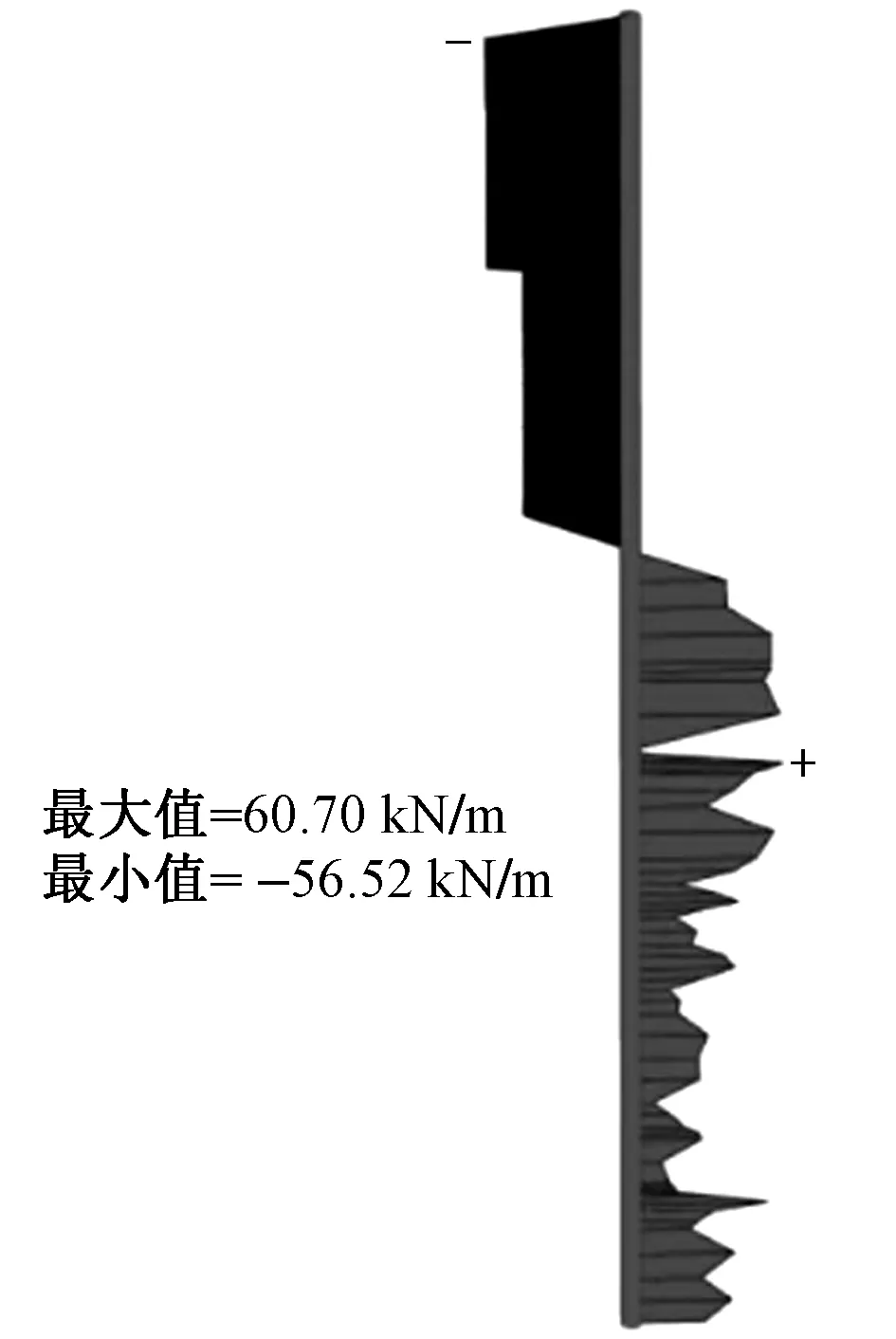
图2 大面积压实填土荷载作用下某基桩侧摩阻力示意图

1.4 基桩负侧摩阻力分布计算模型

本文提出大面积压实填土作用下非饱和软弱土基桩负摩阻力分布计算模型，并与桩基规范模型进行对比，如图3所示。基桩负侧摩阻力的计算图示(图3)主要基于以下因素：1)桩侧土侧摩阻力(正或负)是否发挥至极限，仅与桩-土相对位移有关。根据有关研究成果，桩-土相对位移为2～5mm时，桩侧土正、负摩阻力基本上发挥至极限。2)根据实测及计算分析结果，中性点以上负侧摩阻力未充分发挥区间较小，可按充分发挥考虑，负侧摩阻力按与正侧摩阻力极限值一致考虑，偏于安全且易于工程设计。3)按有效应力法计算的负侧摩阻力与其实测值吻合较差，且分布规律差异较大。4)基于桩土共同作用(发生相对位移)的原则，考虑负侧摩阻力是否发挥及发挥程度，与桩基规范对正侧摩阻力处理一致，使得桩基规范对同一原理下的负摩阻力/正摩阻力的计算达到了一致、协调。5)采用公式(1)计算基桩的负摩阻力。

Qgn=ui∑qsili

(1)

式中：qsi为桩侧土负摩阻力，其值按正极限侧摩阻力qsik取用；其他参数的含义与桩基规范相同。

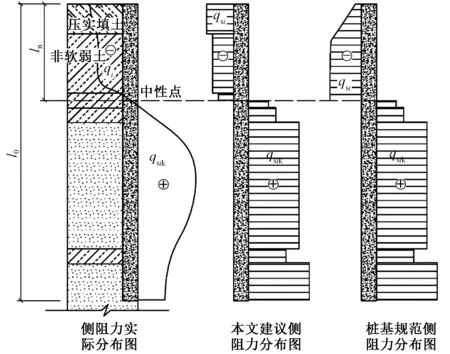
图3 本文基桩负侧摩阻力分布计算模型与桩基规范模型对比示意

2 中性点确定方法

2.1 按变形相等的原则确定负摩阻力中性点

桩基规范对中性点的深度确定进行了原则性规定，即“中性点深度ln应按桩周土层沉降与桩沉降相等的条件计算确定”，但未给出具体的计算方法。要确定中性点的位置，需获得桩周土沉降曲线和桩身沉降曲线，此两条曲线的交点就是中性点的位置。桩周土沉降曲线与土的固结有关；桩身沉降包括桩端沉降(与桩端荷载作用下土的固结有关)和桩身弹性压缩量，一般情况下桩身的弹性压缩量可忽略不计。对于非饱和软弱土，确定“桩侧软弱土层”的下限深度就很困难，也就无法根据桩基规范查表(表5.4.4-2)确定中性点深度ln。为获得较可靠的中性点深度ln值，本文仍采用按桩土相对变形相等的方法确定中性点，但需考虑时间效应，且利用大面积荷载作用下的实测沉降数据，根据实测桩侧土沉降值拟合桩侧土沉降，进行桩侧土阶段沉降、分层沉降及最终沉降的估算。

2.2 按土层固结度考虑中性点的时间效应

负摩阻力是由桩侧土层的固结沉降所引起的，负摩阻力产生前(成桩前)这部分沉降变形已经发生，不会对基桩产生负摩阻力，因此应将成桩前因大面积压实填土压密其下非饱和土层发生的沉降扣除。负摩阻力的发展过程主要是指基桩成桩、加荷及基桩桩端土沉降变形至稳定，其时间长短取决于桩侧土固结完成的时间和桩端下土层在基桩荷载作用下沉降完成的时间，当后者先于前者完成时，则负摩阻力达到峰值后稳定不变；反之，当桩的沉降迟于桩侧土的沉降时，则负摩阻力达到峰值后又会有所降低。负摩阻力产生和发展均会导致中性点深度发生变化。

本文通过大面积压实填土作用下非饱和桩侧土沉降变形曲线和考虑成桩及加载时间基桩变形的方法来考虑中性点的时间效应。通过计算桩侧土各土层分层沉降，并考虑成桩时桩侧土固结度ui，即乘以(1-ui)获得各分层土剩余沉降量，桩侧土自桩端起算的剩余分层沉降自下而上累加后的沉降量与基桩沉降相等的点即为考虑时间效应的中性点。根据桩端以上各分层土沉降和与桩端沉降相等的公式(2)，确定中性点的位置，即分层沉降sn,sn-1，…，sn-j之和与基桩沉降sp相等，则沉降为s1,s2，…，sj-1的分层厚度之和即为考虑时间效应后中性点深度ln。

(2)

式中：ui为成桩时刻桩侧第i层土的固结度；si为第i层土分层沉降；j为从桩端向上累计至中性点深度的土层数。

3 单桩负摩阻力计算方法

3.1 计算流程

根据1.4～2.2节对桩侧土沉降变形计算方法、中性点确定方法及基桩负摩阻力时间效应考虑的研究和分析，归纳总结大面积荷载作用下非饱和软弱土单桩负摩阻力计算流程，具体如图4所示。

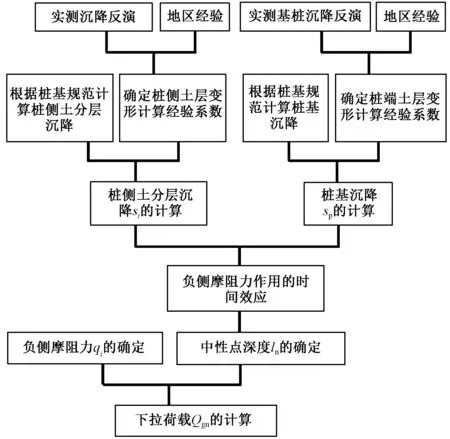
图4 单桩负摩阻力计算流程图

3.2 计算步骤及参数

单桩负摩阻力具体实施步骤如下：

(1)根据沉降观测点数据，采用对数曲线对各观测点进行数据拟合，确定各点的最终沉降s预测。

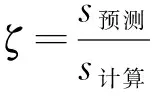
(4)根据地质勘察成果，基桩及桩侧土的变形计算模型，根据地基处理规范公式(式(5.2.12))对桩侧各土层分层沉降进行计算，并乘以场区沉降计算经验修正系数ζ及1-ui后即为桩侧各层土在成桩后发生的沉降s1，s2，…，sn。

(5)根据地质勘察成果提供的地层变形计算参数，按桩基规范计算基桩沉降，基桩沉降乘以场区沉降计算经验修正系数ζ后即为基桩在荷载作用下的沉降sp。计算基桩桩端沉降时，应视情况考虑桩身压缩量，当基桩较短时，可忽略桩身压缩量。

(6)根据桩端以上各分层土沉降与桩端沉降相等来确定中性点的位置，即沉降为s1,s2，…，sj-1的各分层土厚度之和即为考虑时间效应后中性点深度ln(式(2))。

(7)采用式(1)计算基桩的负摩阻力。

按(1)～(7)步骤确定的基桩负摩阻力即考虑了桩侧土固结和成桩等时间效应的基桩负摩阻力。

4 工程实例

某工程场地形成时进行了大面积压实填土工作，填土厚度4～6m，场地地层参数见表1。考虑时间效应的负摩阻力计算相关步骤如下。

4.1 场区沉降计算经验系数的确定

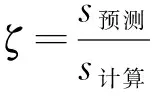
4.2 中性点的确定

根据该工程某一桩基方案初步设计条件，该建筑物承台基底埋深2.5m，该区域的填筑高度约4.0m，承台下布置2根钻孔灌注桩(按单桩计算)，设计桩长22.0m，桩径600mm。根据桩基规范及4.2节确定的沉降计算经验系数、沉降观测数据，可计算得出此桩基的沉降量为16.5mm，固结度u=0.58。根据该承台位置土层分布情况，利用根据地基处理规范式(5.2.12)计算桩基周围土层的沉降，按桩周土层沉降与基桩沉降相等的条件计算确定中性点深度ln，可以得到在基底下5.96m深度处估算成桩后桩周土沉降量约为16.4mm(表1中加粗数据之和)，得到桩基的负摩阻力中性点深度ln=5.96m。

桩基中性点深度计算 表1

4.3 基桩负摩阻力的计算

根据式(1)及计算确定的中性点深度，计算的单桩负摩阻力如下：

若按桩基规范不考虑时间效应，中性点深度为17.6m，则负摩阻力：

不考虑成桩时土层已发生的固结(时间效应)计算的负摩阻力很大，明显不合理。

5 结论

(1)基于一般负摩阻力发生时桩-土相对位移达到极限侧阻力发挥的水平，基桩负侧摩阻力按正摩阻力取值，此取值原则与实测、定性分析及正侧摩阻力取值原则一致。

(2)对于大面积荷载作用下非软土土层中基桩负摩阻力中性点的确定，应按桩及桩侧土变形相等的原则进行。采用本方法时，桩及桩侧土变形计算的可靠性是关键，可采用基于实测数据反演计算沉降经验系数。

(3)确定基桩负摩阻力中性点时，应考虑大面积荷载与成桩等的时间效应。本文采用基于实测数据拟合曲线确定土层变形，从而进行桩侧土固结度估算的方法，有效地解决了非饱和土固结度的估算问题，从而解决了基桩负摩阻力计算的时间效应问题。

(4)基桩负摩阻力作用及影响因素很多，很难准确计算，实际工程中需结合具体工况综合分析，确定符合实际情况的估算方法，还应根据不同桩型、桩-土相对位移的时间效应等对中性点处桩身轴力、承载力等进行验算，并根据实际情况，采取减小负摩阻力的辅助措施。