特高拱坝变形监测的分区及其模型构建方法

胡 江，马福恒，王春红

(1.南京水利科学研究院水文水资源与水利工程科学国家重点实验室，江苏 南京 210029；2. 南京瑞迪水利信息科技有限公司，江苏 南京 210029)

我国已建成一批200～300 m级的特高拱坝，其中多座进入了蓄水和运行期[1-4]。建成世界一流的特高拱坝只是第一步，保障工程全生命周期安全的道路更漫长，任务更艰巨[5-6]。工程实践表明，可靠的安全监测和预报模型、准确的性态分析和诊断是保障工程安全的重要途径。

传统多元回归模型(hydrostatic season time，HST)将变形分离为水压、温度和时效3个部分，并假定温度呈年周期性变化，库水位、环境温度间不存在共线性，以此预测一定环境、荷载组合时的变形值，判别结构的性态。HST模型易用，结果易于解释，因此得到了广泛的应用[1]。然而，HST模型有其局限性。首先，它假定坝体为稳定温度场，不适用于初蓄期、初期运行期等情形。对此，有学者提出了基于实测温度的改进模型(hydrostatic temperature time season，HTTS)，以反映坝体的非稳定温度场特性，在一定程度上提高了模型精度[7]。其次，HST模型多为单测点模型，难以反映空间变形性态。顾冲时等[8]应用场论建立了空间位移场的监测模型。黄铭等[9]建立了双空间位移监测模型，推导了模型的简化式。李端有等[10]建立了拱坝一维多测点位移监测模型，可反映一维方向上的位移分布状态。何金平等[11]利用Bayes理论，以方差为特征参数建立了多测点监测模型。然而，多测点监测模型存在对变形规律性反映不够协调的问题[10]，面板数据模型考虑了测点间的联系和异质性，既可减少变量间的多重共线性，又可描述测点间的相关性[12-14]。为此，面板数据模型被引入基于HST模型的大坝变形和渗流监测领域，并验证了其可靠性和有效性[15-16]。

本文应用主成分分析法(principal component analysis，PCA)，选取模型典型实测温度因子；融合PCA和层次聚类法，提出主成分层次聚类法(hierarchical clustering on principal component，HCPC)，依据实测时间序列，采用HCPC法对变形测点分区；基于HTTS模型建立各分区的面板数据，通过统计检验，确定面板数据回归模型类型；构建各分区的面板数据回归模型，并通过分区及其面板数据回归模型的截距项、系数等的比较分析，识别坝体的变形特征。以一特高拱坝为例，验证本文方法的可靠性和有效性，并对其变形性态进行了评判。

1 分区安全监测模型的构建方法

1.1 基于HCPC法的分区构建方法

PCA和分层聚类都是变量相似性度量工具。当2种方法均采用欧氏距离度量时，可融合得到HCPC法，从而更好地描述变量间的关系。

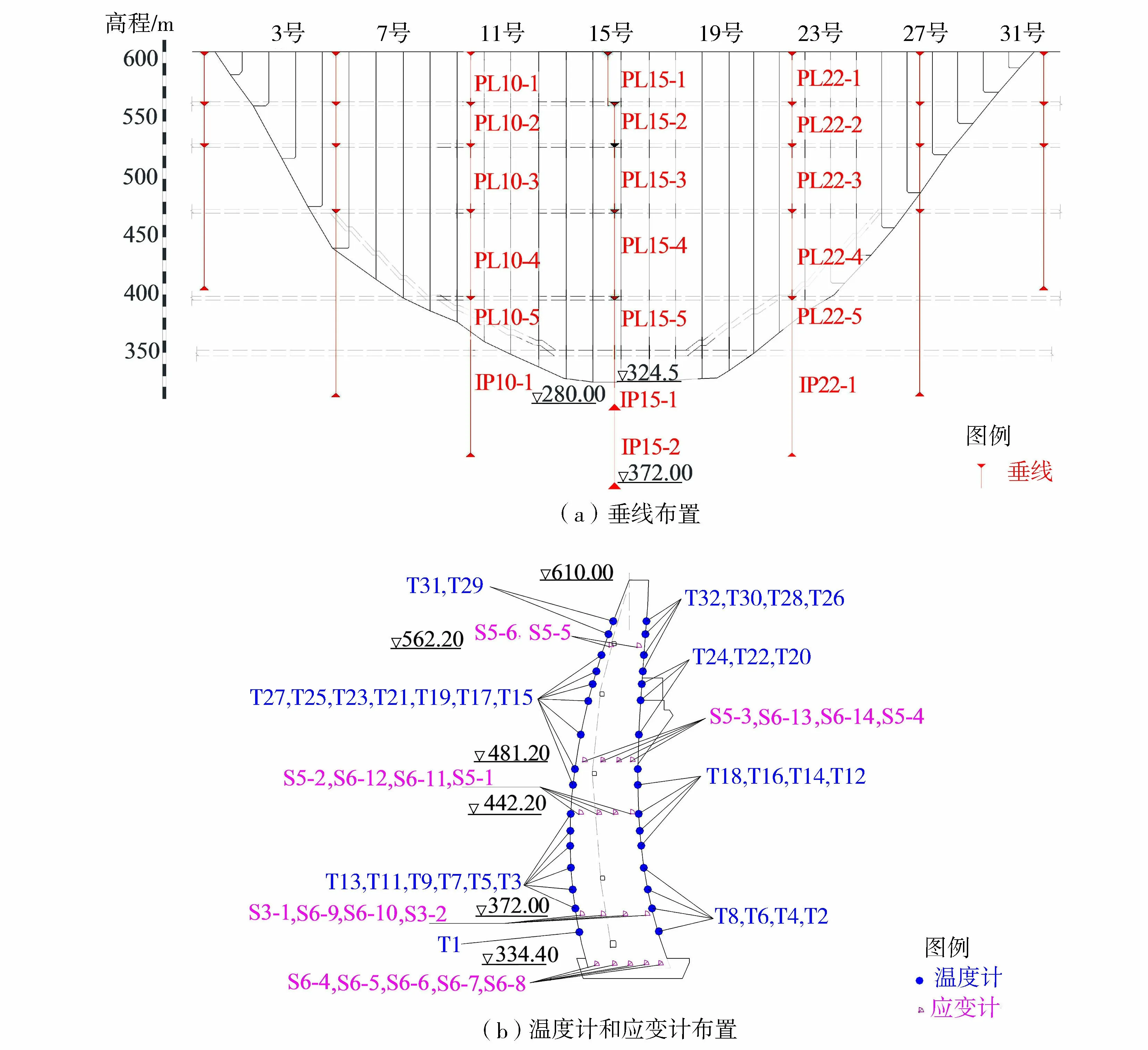
对于数据集XKJ(K为观测点个数，J为观测数)，PCA的核心思想是采用S个(S

(1)

图1 HCPC法的实现流程Fig.1 Flow chart of HCPC method

组内方差表征了组内变量的同质性，Ward准则在聚类时使每个步骤中组内方差增长最小，即组间方差减少最小。确定分组数是聚类分析的核心问题。分层聚类本质是一种嵌套分区，最底层上每个变量均是一个小组，最顶层上所有变量都归属同一个大组。可根据组内方差的增长情况判断最优的聚类分组结果。当分组数从Q-1到Q时的组间方差增加值ΔQ远大于从Q到Q+1时的增加值Δ(Q+1)时，最优分组数为Q组。可采用2种方法获得最终的聚类分区，一是保持分层聚类得到的Q个分组；二是借助K-means算法，将分层聚类结果作为初始分区，通过若干次迭代获得改进的分区结果，迭代过程中通过组间方差的比值判断。通常，初始分区不会被完全替换，而是得以改进。

变量的分层聚类分区结果可表示在主成分映射图上或树形图上。2种结果可视化方法相互补充、交叉验证。HCPC法的实现步骤如图1所示。

1.2 基于面板数据模型的分区监测方法

面板数据是既有时间维度又有横截面维度的二维数据[13-14]。它有诸多优势，如能提供大量的数据，从而降低解释变量间的多重共线性，提高模型监测的有效性；又如能控制个体无法被观测到的异质性，用个体效应表示。因而，面板数据被广泛应用于社会、经济和工程等多个领域[13-14]。

一般地，线性面板模型可以表达如下：

yit=αi+βixit+uit

(2)

式中：yit——因变量；i——测点编号；t——观测时间；xit——变量；α——常数项或截距项；β——模型参数；uit——随机随机误差项，其均值为0。

通常对回归参数、误差和外延性做出假设，从而对面板数据模型进行分类。最常见的是假定截距项和系数项相同，即αi=α，βi=β时，式(2)可以简化为

yit=α+βxit+uit

(3)

式(3)为混合模型，即无测点影响的不变系数模型。这种模型与一般的回归模型无本质区别。而当αi≠α，βi=β时：

yit=αi+βxit+uit

(4)

式(4)表示在横截面上存在测点影响，但变量的结构参数在不同横截面上是相同的，不同的是截距项，测点的差异可以用截距项αi的差别来说明，故称为变截距模型。按其截距项是否和变量相关，又可将其分为固定效应和随机效应模型[13-14]。一般采用如下检验方法判定面板数据模型分类：

(5)

采用F检验，若接受H2，则符合不变截距、不变系数模型。采用Hausman检验，若拒绝H2，则需检验H1。若接受H1，则符合变截距、不变系数模型；反之，则符合变系数模型[13-14]。即通过F检验判断混合效应和固定效应模型；通过Hausman检验，判断随机效应和固定效应模型。

1.3 特高拱坝变形分区监测模型的构建方法

特高拱坝变形分区监测模型构建方法分4个主要步骤：(a)时间序列的预处理。进行异常值分类和判别，具体可参考文献[18]；对时间序列标准化、插值处理，以获得平衡的多测点多变量时间序列。(b)基于时间序列的变形多测点聚类分区。通过PCA筛选得到典型实测温度变量；依据变形测点时间序列，采用HCPC法度量测点间变形规律的相似性，确定分区数，基于HTTS模型构建分区面板数据，绘制测点分区结果的主成分映射图、树形图；将分区聚类结果映射在坝体上，结合环境、荷载变量的变化，综合分析聚类分区结果。(c)分区监测模型的构建。基于分区面板数据，通过F检验、Hausman检验等实现变系数、混合、固定和随机效应等面板数据模型类型的判断，构建各分区的面板数据回归模型。(d)模型结果的分析。通过回归模型的截距、回归系数等的对比分析，判断各变量与变形间关系，辨识各分区变形特征，进而识别坝体空间变形特征。

2 应 用 实 例

2.1 工程概况和监测仪器布置情况

某混凝土双曲拱坝坝顶高程610.00 m，建基面开挖高程324.50 m，最大坝高285.50 m。坝顶长度中心线弧长681.51 m，共31个坝段。水库正常蓄水位600 m，死水位540 m，汛期运行限制水位560 m。2013年5月，大坝导流底孔下闸蓄水，2014年3月大坝混凝土全线浇筑到高程610.00 m。

在5号、10号、15号、22号、27号坝段内各布置1组垂线系统，正垂线(PL)测点布置在高程610.00 m、563.25 m、527.25 m、470.25 m、395.25 m、347.25 m，正垂线对应的坝基布置倒垂线(IP)。在6号、10号、16号、22号、27号、29号坝段等6个坝段布置坝体混凝土温度监测断面，布设高程的上游和下游坝面各布置1支温度计(T)观测环境温度。坝体内部采用应变计(S)的测温传感器观测(实测温度变量Sn-i为n向应变计第i测点实测温度)，布设高程上各设3支，位于坝体上游侧、中部和下游侧。本文重点分析的10号、15号、22号这3个坝段垂线布置及16号坝段的坝体混凝土温度计布置情况如图2所示。库水位变化过程线如图3所示，至2018年6月拱坝共经历了5个完整的加载和卸载过程。考虑到坝顶高程的垂线测点的起测时间为2014年7月，本文分析的时间序列为2014年7月—2018年6月，10号、15号、22号这3个坝段的垂线测点的径向位移过程线如图3所示。

图2 监测仪器布置(单位:m)Fig.2 Layout of monitoring instruments (units: m)

图3 库水位和垂线测点径向位移变化过程线Fig.3 Change process curves of reservoir water level and radial displacements of focused plumb lines

2.2 测点分区

对垂线测点进行PCA，第一、第二主成分解释了98.9%的总方差。为此，在第一、第二主成分上采用HCPC法进行测点分区。分组数从(Q-1)到Q时的组间方差增量如图4(a)所示，前序值分别为89.07、22.71、19.32和5.44，组内方差比值分别为0.61、0.46、0.67和0.51，树状分区建议的最优分区数为4个(图4(a))。同时，采用因子映射图得到了分区结果(图4(b))，在第一、第二主成分较好地分离了4个区。映射到坝体下游面的结果如图5所示。

依据图4、图5的结果，结合图3的过程线可看出，各高程拱圈变形以拱冠15号坝段为界，拱冠坝段径向位移大于两侧坝段，变形测点的分区呈对称分布，变形协调。

图4 变形测点的树状和主成分映射分区Fig.4 Dendrogram and PCA based zoning maps for focused plumb lines

图5 变形测点分区坝体下游面映射Fig.5 Mapping image of deformation monitoring points on downstream face of zoned dam

2.3 分区监测模型

拱坝变形受到静水压力、温度及坝体混凝土徐变、基岩蠕变、软弱结构面调整等因素的影响。鉴于工程处于初期运行期，非稳定温度场显著，采用HTTS模型[7, 19-20]进行分区监测。HTTS模型的库水位H采用传统HST模型形式[7-8]。近似分析，将16号坝段的实测温度作为各分析坝段的实测温度，对实测温度变量进行PCA分析，结果如图6所示。根据主成分和主要变量间的关系，最终选取的实测温度变量为S6-9、S6-4、T30。此外，考虑到蓄水和初期运行期时效先迅速增大随后趋缓的特征，采用指数时效V，其形式为e-θ，θ=0.01t，t为观测日至始测日的累计天数；针对完整的加载卸荷周期存在的徐变恢复变形，根据函数逼近原理，还加入了年周期项S1、S2，分别为S1=sin(2πt/365)，S2=cos(2πt/365)。

图6 温度因子的PCA分析Fig.6 PCA analysis of temperature factors

各分区监测模型的变量与相应的HTTS模型相同。实际经验表明，若条件数大于100则说明变量间存在相似共线性。利用kappa函数计算自变量矩阵的条件数，以分区1为例，计算得到的条件数为198.98，表明变量间存在中等相似共线性。通过F检验，各分区显著水平p<2.2×10-16，可知建立个体固定效应回归模型更合理，通过Hausman检验，随机效应不显著，且固定效应和随机效应模型系数相等。因此，最终选取固定效应面板数据回归模型。为便于对比分析，将各变量标准化，在此基础上对各区模型进行估计，结果见表1，部分垂线测点HTTS模型结果见表2，其中显著水平Pr<0.001时表示回归系数显著不为0，R2表示模型可以解释位移方程的程度。

表1 各分区固定效应模型的参数拟合结果

表2 部分测点的HTTS模型的参数拟合结果

2.4 结果分析

由表1可知，在5%水平下，分区1、2、3的各影响系数都具有显著效应，但不同分区变量的影响大小存在差异。具体阐述如下：

a. 径向位移与库水位呈显著正相关，与库水位相关性良好，即库水位上升，坝体向下游变形，且低高程的系数比高高程小，两侧坝段比拱冠坝段小。考虑到高高程的位移值是同一垂线系统各垂线段叠加的结果，这符合一般的规律。

图7 典型温度测点的测值过程线Fig.7 Historical change processes of temperatures of typical points

b. 径向位移与372.00 m高程坝体内部上游侧应变计测点S6-9温度测值显著负相关。由于PCA分析仅选取了与主成分最相关的变量，S6-9为坝体内部温度的典型测点，代表了坝体内部温度变化情况(图7)。其系数大小的分区变化规律同库水位一致，即低高程比高高程小，两侧坝段比拱冠坝段小。可见，封拱后的温度回升使大坝存在整体向上游变形的增量，与静水压力导致的坝体径向位移方向相反。已建的多座特高拱坝的观测结果也表明，在封拱灌浆后，坝体内部都不同程度出现了温度回升现象[21]。相反地，径向位移与334.40 m高程坝体内部上游侧应变计测点S6-4温度测值显著正相关。S6-4代表了坝体内部的温度稳定区域，主要受环境温度的影响，由于库水温垂直分层逐渐形成，库底水温下降，使得坝体有向下游变形的增量。但相比而言，S6-4的回归系数比S6-9要小得多，换言之，封拱后的温度回升影响更显著。

c. 指数时效显著正相关，且系数的分区变化规律与库水位、坝体内部S6-9测点温度类似。指数时效因子为混凝土徐变、基岩蠕变等时效变形的综合表现，从其系数可以看出，指数时效在初期运行期对特高拱坝的影响显著，时效表现为坝体整体向上游变形。大坝结构、基础岩体及库盆的调整对坝体会产生一定影响。事实上，该坝在蓄水后各测线的谷幅持续收缩，拱坝坝体受到了两岸坝肩岩体的显著挤压作用，谷幅收缩是坝体倾向上游变形的主要驱动力。采用指数时效因子较好地模拟了这一特征，蓄水后增长迅速，之后呈现增量减少趋势，但谷幅变形量值尚未完全收敛。此外，周期徐变恢复项对各分区的影响也较为显著。

d. 相比较，分区4的拟合精度相对较差，受库水位影响相对较小，时效也减少。但总体而言，其变形规律与其他3个分区类似。

e. 对比表1、表2可知，变量间存在相似共线性时，并未影响预测结果。但由于变量间存在相似共线性，HTTS模型中变量的显著性检验较面板模型要差，导致统计推断上无法合理地给出各变量对变形影响的真正大小。

3 结 论

a. 结合PCA和层次聚类法提出了HCPC法，得到了基于监测时间序列的变形测点分区方法，分区结果与坝体变形规律相吻合。

b. 融合HCPC法和面板数据，提出了特高拱坝变形分区监测及其模型构建方法。通过分区及其模型的截距项、系数等参数的对比分析，可识别各分区及坝体空间变形特征，有较明确的物理概念和空间特性。分区面板数据回归模型既充分发挥了传统模型可分离变量以解释变形机理的优势；还考虑了测点间、分区间的联系和异质性，减少了变量间的多重共线性影响，描述了测点间、分区间的相关性和个体效应。

c. 模型结果表明，特高拱坝初期运行期坝体变形受非稳定温度场和非线性时效影响显著。

d. 大坝变形分区面板数据回归模型是可靠有效的，为特高拱坝安全监测和预报提供了一条新的途径。