基于布隆过滤器和B+树构建倒排索引的电子病历密文搜索
王 莱 周腾达 王正飞 洪佳明
(广州中医药大学医学信息工程学院 广东 广州 510006)
0 引 言
电子病历中包含了许多隐私信息,包括病人的个人信息、性别、年龄、身份证号等,身体情况中单是病史就包括了既往史、现病史、月经史、婚育史等多项内容。如何保护这些隐私信息在云服务(或者外包)环境中不被泄露变得非常重要[1],进一步地,我们还常常需要进行信息检索。
当前大数据发展如火如荼,电子病历数据越来越冗杂,医疗机构信息化建设必须加快。2019年1月,国务院办公厅下发《关于加强三级公立医院绩效考核工作的意见》(国办发〔2019〕4号),要求三级公立医院要加强以电子病历为核心的医院信息化建设,将“电子病历应用功能水平分级”指标列为国家监测指标。按照相关规定,2019年8月底前,各地卫健委须组织三级公立医院完成电子病历的编码和术语转换工作,将全面启用统一的疾病分类编码、手术操作编码、医学名词术语。
加密是电子病历数据的基本要求,有效搜索则是利用与处理电子病历数据的基础技术。但由于隐私信息加密后失去了原有语义,如何对密文进行准确和快速查询成为关键问题。许多研究人员都对密文查询进了研究,Song等[2]首次提出了对密文进行搜索,用户采用对称加密算法完成加密后发送给服务器,查询时,用户采用哈希函数建立陷门(trapdoor)并发送给服务器,服务器根据陷门完成搜索后,返回密文给用户。与Song等类似,Boneh利用哈希函数和双线性对映射生成密文,用户关键词映射为搜索凭证发送给服务器完成对密文的搜索,该方法为非确定性加密,服务器端无法根据密文判断其中包含的关键词。但这些方法都需要对所有文档进行搜索,搜索效率低下。Wang等[3]根据关键词的出现频率先进行排序,实现密文的搜索,但排序会在一定程度上影响安全性[4]。
针对密文搜索效率低下的问题,Goh[5]提出一种基于布隆过滤的z-index方法,该方法建立在布隆过滤器的基础上,为每个文档增加对应的BF数据结构。该文定义和实施了四个函数:Keygen(s),Trapdoor(Kpriv,w),BuildIndex(D,Kpriv),SearchIndex(Tw,ID)。其中:Keygen()用来生成包含多个子密钥的主密钥;Trapdoor()用来生成关键词对应的陷门;BuildIndex()用来为每个文档构建索引;SearchIndex()用来根据用户提交的陷门完成对加密文档查询。该方法的主要优点是能够利用哈希函数快速计算的特点,迅速从密文中直接查询到匹配的文档。但是该方法需要对文档中所有布隆过滤器进行遍历,才能搜索到匹配的文档,极大地影响了系统的性能,特别是在大规模数据处理场景中不适用。
Demertzis等[6]对于SE(Searchable Encryption)领域十分关注,提出了两种在保证安全性的前提下提升工作效率的方案,其具有可调整局域性和线性空间,提升了读取效率和减少了端到端的搜索时间,并可以调优以实现空间、读取效率、位置、并行性和通信开销之间的权衡。Demertzis等[7]试图在效率和安全性之间进行权衡的另一个方案则基于可搜索对称加密(SSE)技术,主要用于关键字搜索,使用了树状索引的范围覆盖技术将范围搜索简化为多关键词搜索。
本文在z-index的基础上对布隆过滤器BF进行改进,把布隆过滤器组织成倒排文件,并建立B+树,充分利用了布隆过滤器的过滤效率高[8]和倒排索引的全文快速查询特点,从而提高电子病历密文查询性能。
1 电子病历密文搜索模型
为了支持对加密电子病历的密文查询,设计了电子病历密文搜索模型,如图1所示。数据拥有者根据电子病历文档中所包含的关键词,为其建立索引,然后把加密后的电子病历和其对应索引提交给云服务器;用户查询电子病历时,提交陷门(加密后的关键词)给云服务器,云服务器根据陷门在索引中进行查询,在不解密情况下找到匹配的电子病历密文,并把密文返回给用户,用户收到密文后再解密。
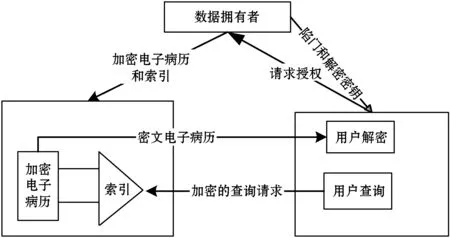
图1 电子病历密文搜索模型
这种模型很好地保护了用户隐私信息安全。一方面,由于用户只是提交了陷门,用户的查询关键词不会暴露给云服务器,所以云服务器无法直接获得用户的查询请求。另一方面,云服务器在查询过程中,使用密文索引直接进行查询,无须对密文电子病历进行解密,更好地保护了密文电子病历隐私信息的安全。在该模型中,为进一步提高对索引检索的效率,本文把布隆过滤器组织为B+树,检索效率从原来的O(n)提高到O(logmn)。
2 方法设计
2.1 布隆过滤器创建
布隆过滤器(Bloom Filter,BF)起源于1970年,由Burton Bloom首次提出,是一种高时空效率的数据结构,由一个一定长度(比如128 bit位)的二进制向量和一组相互独立的哈希函数组成[9]。布隆过滤器可以用来检查一个元素是否出现在一个数据集合中,具有很好的过滤效果。
对于特定关键词W,建立布隆过滤器过程如下:
(1) 使用密钥生成算法Keygen(s):给定一个安全参数s,生成主密钥Kpriv=(k1,k2,…,kr)←R{0,1}sr,其中主密钥包含r个子密钥,每个子密钥的长度为Sbit位。
(2) 使用陷门生成算法Trapdoor(Kpriv,w):给定主密钥Kpriv和查询关键词w,生成陷门Tw=(f(w,k1),f(w,k2),…,f(w,kr))∈{0,1}sr,其中f是伪随机函数,本文使用哈希函数HMAC-SHA1作为伪随机函数:{0,1}*×{0,1}160→{0,1}160,允许处理任意长度关键词。对于每个关键词w,进行r次哈希处理,每次使用一个子密钥kr,每次会产生一个陷门值。产生的陷门要保存好,因为在后续的索引构建和用户查询过程中将会继续使用。
例:电子病历中的主诉文档包含关键词“糖尿病”,假定布隆过滤器长度为128 bit。(1) 生成主密钥Kpriv=(k1,k2,k3,k4);(2) 计算“糖尿病”的陷门和编码词,x1=f(“糖尿病”,k1),x2=f(“糖尿病”,k2),x3=f(“糖尿病”,k3),x4=f(“糖尿病”,k4)),c1=f(Did‖x1),c2=f(Did‖x1),c3=f(Did‖x1),c4=f(Did‖x4);(3) 对编码词c1,c2,…,c4进行哈希计算pr=Hr(cr),得到p1=79,p2=25,p3=48,p4=103,则布隆过滤器相应的位置“1”,如图2所示,在布隆过滤器的第25、48、79和103位置为1,其余为0。
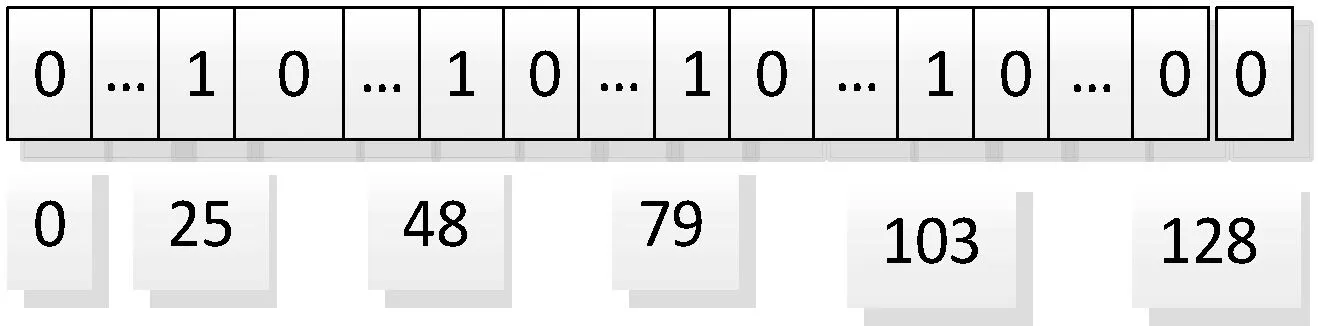
图2 布隆过滤器
2.2 基于布隆过滤器的倒排索引创建(BF_II)
为电子病历中所有的关键词建立好布隆过滤器后,需要构建基于布隆过滤器的倒排索引,如图3虚线部分所示。倒排文件中包含倒排列表和词典两部分。倒排列表包含某一关键词的所有文档的地址集合,与传统倒排文件相同;词典包含BFi和指针pi,词典中用BFi代替了传统的关键词。
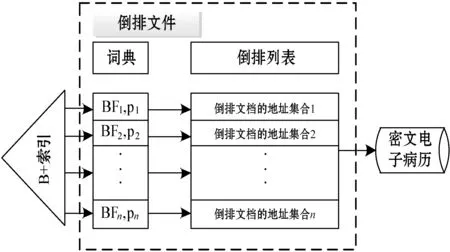
图3 基于B+树的倒排索引构建
需要注意的是,本文中BF与z-index创建BF有所区别,z-index为每份电子病历建立布隆过滤器,而本文通过分词器从电子病历提取关键词,然后为每个关键词构建布隆过滤器,并代替倒排索引中的词典。在建立布隆过滤器的过程中,把包含同一个关键词的电子病历放到同一个集合中。如果多份电子病历中都包含了关键词“高血糖”,那么就将这些电子病历的地址放到同一个集合中,其他的关键词重复上述步骤,最后得到本文的倒排索引。此外,可将BF按照频次高低进行排序,进一步提高查询效率。
将布隆过滤器与倒排索引结合起来,一方面充分利用了布隆过滤器的高空间过滤性和倒排索引的高效文本搜索性能;另一方面将明文的关键词转换为布隆过滤器,还能保护用户查询请求的安全和云服务器中数据的安全。
2.3 基于B+树和布隆过滤器的倒排索引(B_BF_II)
利用布隆过滤器查询时,由于词典中的词表BF是有序的,可以采用二分查询算法,查询代价为O(log2n),但是在大数据环境中,倒排索引空间开销大,内存难以存放,将极大降低系统查询性能[10]。因此,在BF_II的基础上,提出一种改进的基于B+树的倒排文件(B_BF_II),利用B+树快速查询的特点,为倒排文件中的词典建立B+树索引,如图3左部所示。在B+创建时,把词典中的BF作为叶节点,然后逐步建立中间节点,直至根节点。
2.4 电子病历密文查询算法
把加密的电子病历和倒排索引以及B+索引发送给云服务器存储。查询时,用户提交陷门,首先对B+检索,快速定位到倒排索引中词表,然后找到布隆过滤器对密文直接筛选。
对加密数据的查询,分两步进行:(1) 客户端生成陷门Tw,对B+树进行查询,找到满足查询条件的叶节点,获得相应电子病历的id,根据id读取对应的加密电子病历文档并传输至客户端;(2) 客户端解密获得明文电子病历。
算法1基于BF和B+树加密电子病历查询
输入:搜索的关键词Wi,Did(电子病历编号)。
输出:密文电子病历。
1. 用户计算陷门Tw=Trapdoor(Kpriv,wi)=(x1,x2,…xr),并发送给服务器。
2. 服务器接收到陷门Tw。
(1) (c1=f(Did‖x1),(c2=f(Did‖x2),…,cr=f(Did‖xr))∈{0,1}sr。
(2) 计算编码词的位置,选取r个哈希函数H1,H2,…,Hr,计算p1=H1(c1),p2=H2(c2),…,pr=Hr(cr)。
(3) 把布隆过滤器BF中p1,p2,…,pt的位置上修改为1,没有修改过的仍为0,得到该关键词的布隆过滤器。
(4) 查询B+树,从根节点开始,直至叶节点。如果找到满足条件的叶节点(倒排索引中的词条),继续步骤3,否则停止搜索,返回未找到密文电子病历信息。
3. 服务器根据倒排索引中的词条所对应的指针Pi,搜索到倒排文档的地址集合,然后返回用户密文电子病历。
4. 用户解密,获得明文电子病历。
3 系统分析
3.1 安全性分析
(1) 服务器安全性。服务器存储了电子病历密文和索引两部分,前者采用了加密算法(如AES、DES)进行加密以保证其安全性,能够抵抗选择明文攻击,本文不作讨论。后者是根据前者的关键词经过一系列转换得到,转换过程主要使用了哈希函数保证其安全性。如图3所示,索引结构中包含了BF、倒排文件和B+树,由于倒排索引和B+都是建立在BF的基础上,安全的关键在于BF上。在BF的构建过程中,首先通过用户的安全参数s动态生成r个密钥ki,只要用户安全参数s不泄露,即使攻击服务器端获得用户的身份信息,也无法获得密钥。其次在产生陷门时,采用了伪随机函数(HMAC-SHA1),对于布隆过滤器中的每个词条进行了r次哈希处理,能够抵抗选择明文攻击(Adaptive Chosen Keyword Attack,IND-CKA)[11]。在倒排文件中,BF与地址p连接成为词典,BF是有序的,但并不会给攻击者带来任何机会,因为从BF的构建过程中可以发现,BF有序,但关键词的顺序被打乱,攻击者无法从BF的有序信息得到关键词的顺序关系。类似地,B+树也是根据BF的顺序来构建,攻击者也无法进行选择明文攻击[12]。
(2) 用户端安全性。首先,用户查询电子病历时,向服务器发送陷门,而不是关键词,保证了用户查询使用的关键词不被服务器知道。其次,服务器返回电子病历密文,很好地保护了用户查询结果的安全。
3.2 正确性分析
把加密的电子病历和倒排索引以及B+索引发送给云服务器存储。查询时,用户提交陷门,首先对B+检索,快速定位到倒排索引中词表,然后找到布隆过滤器对密文直接筛选。利用布隆过滤器查询电子病历密文时,不会遗漏任何包含该关键词的电子病历。根据BuildIndex(D,Kpriv),每个关键词都会在布隆过滤对应的r个位上置1。查询时,根据用户提交陷门再重复相同计算,必定也是在相同的r个位上置1,所以只要电子病历包含该关键词,绝对不会遗漏。
但是,布隆过滤器置1时,由于为不同关键词建立索引时,同一个位置可能会重复置1,这样可能产生假阳性(False Positives)。假阳性概率为:
(1)
式中:m是过滤器大小(bit);n是关键词个数;k是哈希函数个数。可以观察到,随着过滤器位数m增加,假阳性概率下降;随着关键词个数n的增加,假阳性概率上升。
3.3 性能分析
在电子病历文档中,常用医学专业词汇关键词个数1 000个左右,假设使用8个哈希函数,那么布隆数组大小为213=8 192 bit,假阳率能够控制在0.01即1/100之内,这样的空间过滤效果能够满足密文电子病历搜索需求。
对于未能过滤掉的伪文档,常见的处理方法是发送给用户,用户解密后发现文档不符合要求再舍弃。当然,发送给用户的密文都需要与访问控制措施结合起来,用户有权限才能获得相关的密文。
作为树形的数据结构的B+树能够多路查找,具有能够保持数据的稳定有序的特点,有良好的查询效率[13],因此B+树被广泛应用于数据库和操作系统的文件系统中,如此广泛的应用足以体现出B+树查询等方面的优势。本文使用B+树将倒排文件组织成BIF,充分挖掘B+树的查询优势。
4 实 验
在实验中,比较了倒排索引(II)、基于布隆过滤器的倒排索引(BF_II)、基于B+树和BF的倒排索引(B_BF_II)方法在创建时的空间代价和查询的时间代价。实验中使用的关键词是从常用临床医学术语中获取,分成1 630和5 295两组。每次实验做10次,取其平均值作为最后实验分析数据。实验中使用的哈希算法为HMAC-SHA1,实验环境为Windows 10操作系统,P4 2.8 GHz的CPU,8 GB的内存。
4.1 构建索引的空间代价
在实验中,对三种不同索引的空间大小进行比较。如图4所示,(a)和(b)比较了关键词个数分别为1 630和5 295时三种索引的空间大小。从实验结果可以得出:布隆过滤器大小由8 bit逐渐增加至128 bit时,BF_II比II的空间稍微减少,这是由于BF过滤器采用位图表示,比关键词所占存储空间相应少一些。而B_BF_II相对另外两种索引空间稍微增加,这主要是因为B_BF_II在BF_II基础上增加了二级索引B+,空间相应地增加了一些。
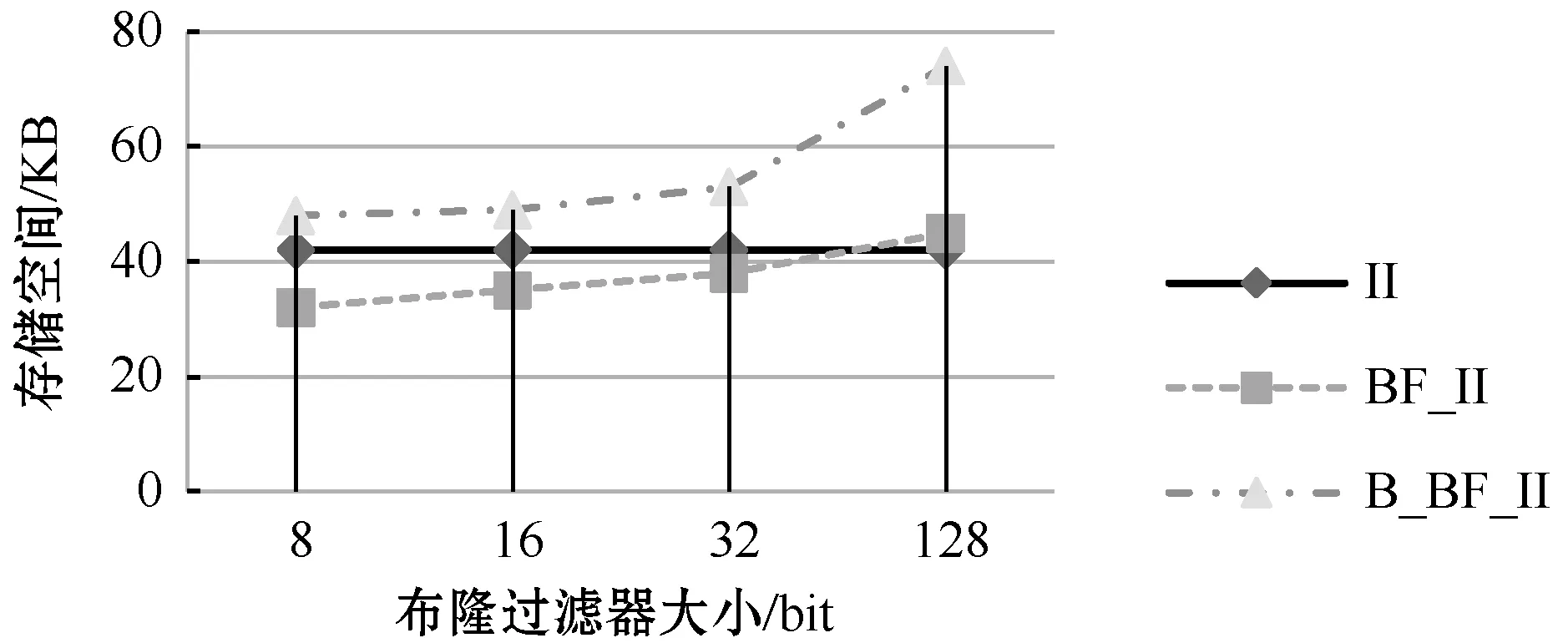
(a) 关键词个数为1 630
4.2 查询的时间代价
用户查询代价是衡量系统性能的最重要指标,尽量减少查询和验证时间是本文研究的一个重要目的。在这个实验中,用户查数据时,采用了单关键词查询和多关键词查询两种方式,例如:单关键词查询疾病为“糖尿病”,多关键词查询疾病为“糖尿病”和“血脂高”。如图5所示,通过单关键词查询的实验结果对比可以得出,BF_II比II的性能稍优,而在BF的位数增加时性能优势稍微有所减少,这是因为在BF位数小时进行比较的位数少,比关键词的直接比较要稍微快一点,所以随着BF位数增加,BF_II的优势就会有所减弱。而B_BF_II在布隆过滤器位数较少时查询代价比BF_II的要高出许多,但是随着BF位数的增加B_BF_II的查询性能体现出很大的优势。所以当BF位数比较大时,B_BF_II的查询代价有明显优势。
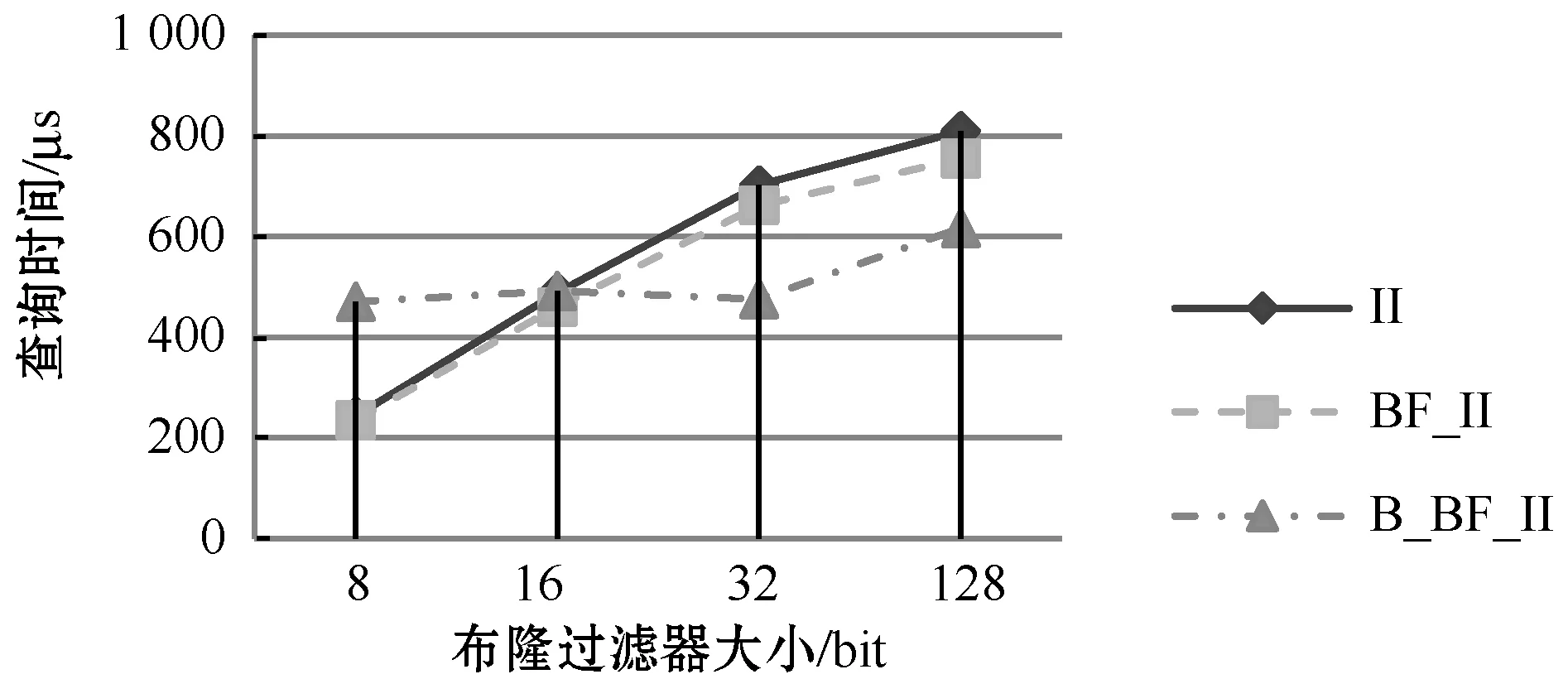
(a) 关键词个数为1 630
多关键词查询的实验结果对比如图6所示,实验结果与单关键词查询结果相似,在BF位数较少时,II与BF_II的性能相近,但BF_II的略优,此时两者都比B_BF_II的性能好。但当BF位数较大时,B_BF_II的查询性能体现出明显优势。
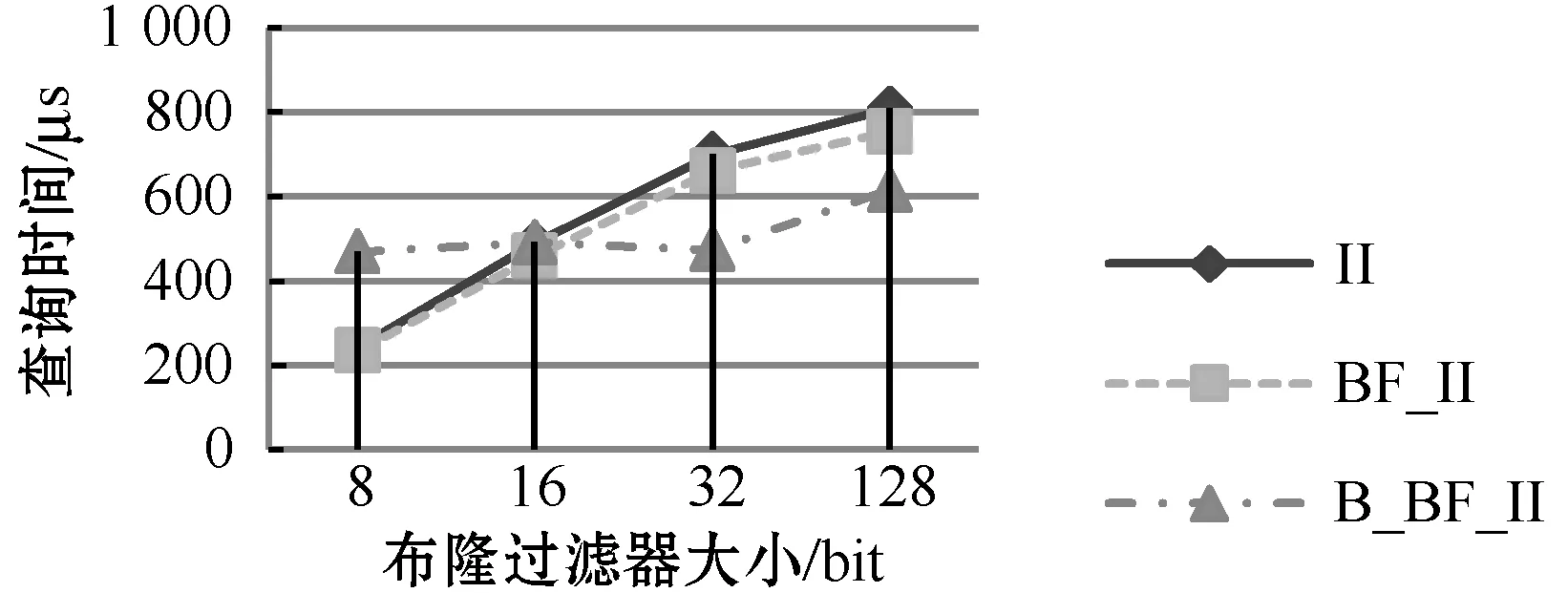
(a) 关键词个数为1 630
4.3 与z-index查询时间代价对比
本文基于z-index对可搜索密文技术进行相应改进。上述实验结果还没有对比本文技术与z-index查询方面的性能。如图7所示,就是本文所说的四种索引之间的查询代价对比图。该实验中BF的大小为128 bit,从实验结果对比可知前三者的查询性能都比z-index有着明显的优势。根据上文的叙述前三者都是倒排索引,而z-index是正排索引,所以从实验结果可以看出,倒排索引在查询性能上拥有良好的优势。
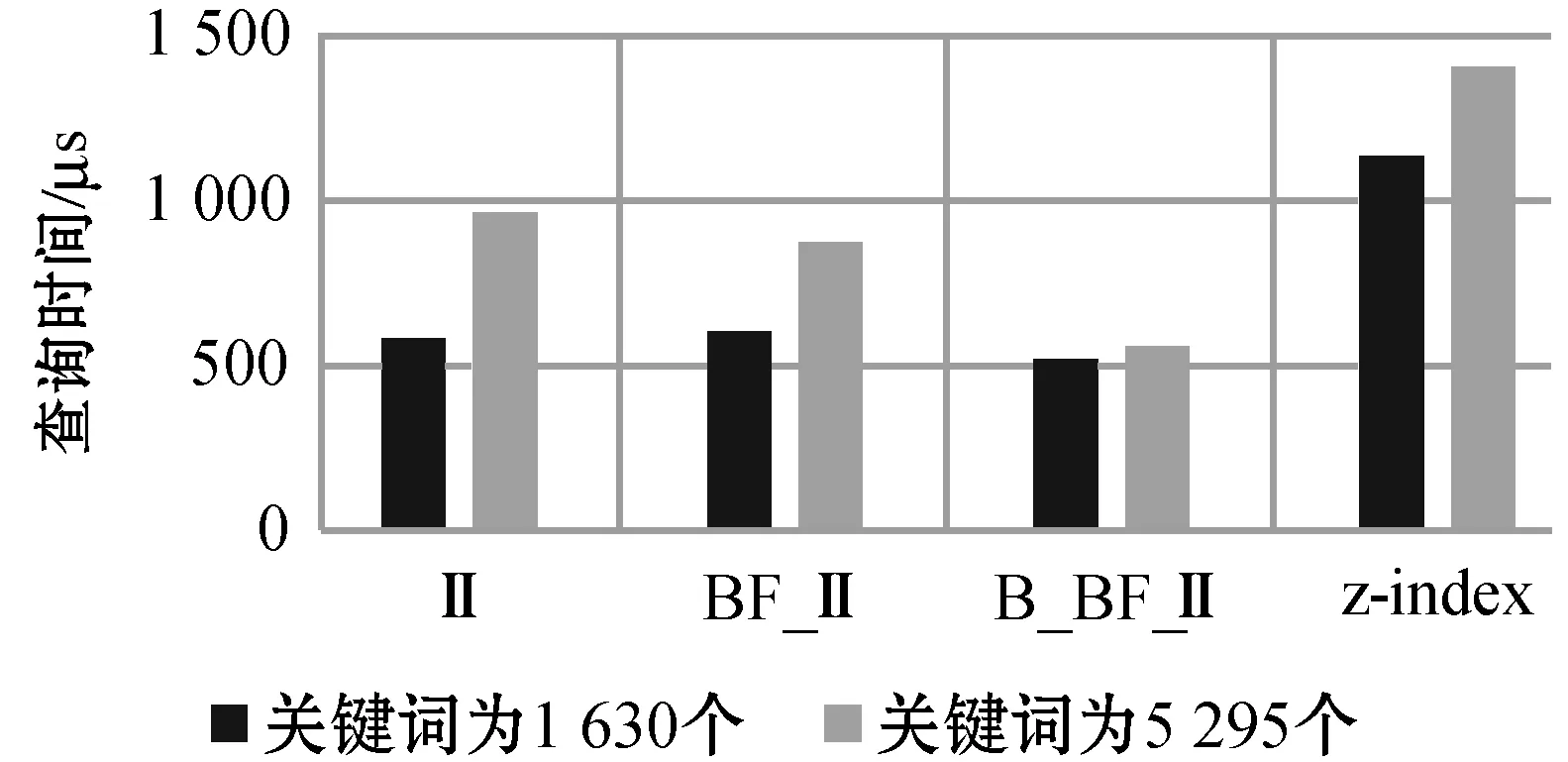
图7 与z-index查询代价的对比
5 结 语
本文中主要讨论如何设计索引,用户通过对索引的查询就能获得密文,而不需要解密,针对现有可搜索密文技术的一些缺陷进行改进,主要采用了基于BF的倒排索引与B+树结合的方法,提高了电子病历的密文查询效率,还能支持布尔查询进行“与”“或”“非”查询,提高检索效率。在医院电子病历的大数据环境如火如荼的今天,本文的研究能够为各大医疗机构提高自己的医疗信息系统的性能或为其他领域的技术研究提供一些帮助,促进医院电子病历系统的革新与改进。

