基于ARIMA模型对中、美、德三国CPI的分析与预测

马瑶 孙中玉 邹益玲

要：居民消费价格指数是衡量通货膨胀的重要指标。运用ARIMA时间序列模型对中国、美国和德国2000年1月至2020年4月的月度居民消费价格指数数据进行分析与建模。首先，通过ADF单位根检验、自相关函数（ACF）图和偏自相关函数（PACF）图来确定模型阶数;其次，通过比较各个模型的AIC与BIC值来确定最佳模型;最后，通过对模型残差序列进行白噪声检验来验证模型的可靠性，并对2020年5—12月各国的CPI指数进行模型预测与分析。结果表明，ARIMA模型能够准确地预测CPI指数的变化趋势，且政府对疫情的干预会对CPI的变化产生重要影响。

关键词：CPI;ARIMA模型;时间序列分析;趋势预测

中图分类号：F726      文献标志码：A      文章编号：1673-291X（2021）08-0001-04

引言

新型冠状病毒肺炎疫情在全世界范围的大面积传播，对世界经济的发展产生重大冲击，以至各行各业大多进入停产停工阶段。为了更加直观快速地了解这次疫情对人民日常生活的影响，本文拟通过时间序列模型来分析居民消费价格指数（CPI）的变化趋势和政府在疫情期间采取的应对政策对CPI变化的影响。CPI（Consumer Price Index）指数一般被用来衡量通货膨胀程度，能反映城乡居民家庭一般所购买的消费商品和服务价格水平的变动情况 （雷鹏飞，2014）[1]。若CPI升幅过大，则表明通胀已经成为经济不稳定因素，国家会有紧缩货币政策和财政政策的风险（Mohamed J.，2020）[2]。因此，对CPI指数的准确预测，不仅能使政府和国家对未来可能发生的经济形势做出准确与及时的判断，而且能够帮助政府对当前不适应未来经济发展的政策进行及时的调整，以便促进经济繁荣、快速发展。

由于不同国家对于疫情的处理方式不同，导致疫情期间各个国家CPI的变化也产生巨大的差异。本文将使用python（3.7.3）语言对中国、美国和德国的CPI月度数据建立ARIMA模型，并验证模型的可靠性，进而对2020年下半年的CPI指数进行预测与分析，分析疫情期间政府的行为对本国CPI变化的影响。

一、数据来源与模型简介

（一）数据来源

本文选取的中国、美国、德国CPI月度数据分别来源于中国国家统计局网站（http：//data.stats.gov.cn/）和全球经济指标网站（https：//zh.tradingeconomics.com/）。

（二）数据预分析

从图1的CPI时序图中可以看出，中国、美国和德国2000—2020年的CPI数据呈现出非平稳性的特征。

（三）模型简介

基本的时间序列模型有自回归（AR）模型、移动平均（MA）模型、自回归移动平均（ARMA）模型以及差分整合移动平均自回归模型（ARIMA）等（Box G E.2008）[3]。ARIMA模型旨在确定最合适的p、d、q参数值，并将其应用于时间序列数据的预测与分析。对于特定的时间序列数据，先根据序列的平稳性确定差分次数d，再依据ACF图和PCAF图来确定AR（p）和MA（q）项的p和q值。

季节ARIMA模型由ARIMA模型和季节性效应模型两部分构成（孙颖，2016）[4] 。其一般形式为：

φp（L）Φp（LS）▽D▽dxt=θg（L）ΦQ（LS）εt

其中，p为自回归系数，q为移动平均系数，d为使非平稳时间序列成为平稳序列所做的差分次数，P为季节性自回归阶数，S为季节性周期，Q表示季节性移动平均阶数。εt表示均值为0，方差为σ2的正态分布。

二、模型识别与建立

（一）平稳性检验

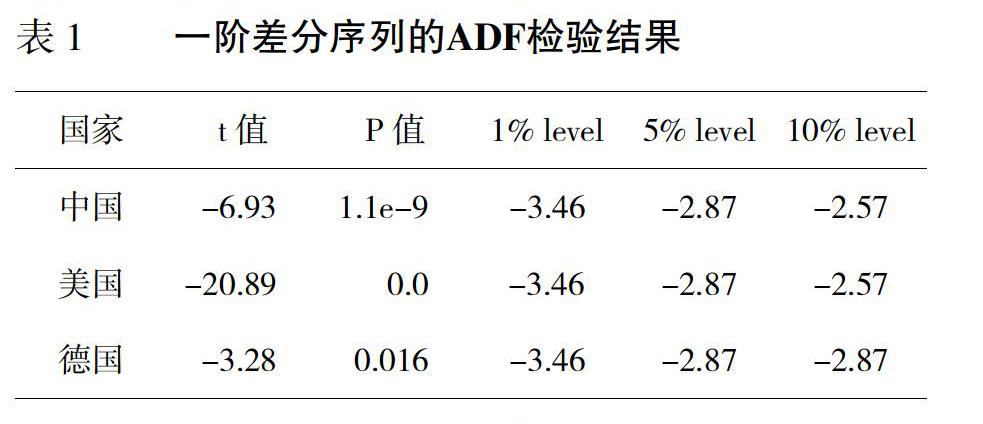
由数据预分析可知，中国、美国和德国的CPI序列为非平稳性序列。为了进一步建模分析，对三個国家的CPI序列进行一阶差分处理使序列平稳化，得到新的时间序列DCPI。为了进一步检验DCPI序列的平稳性，进行单位根（ADF）检验，ADF检验使用T统计量进行检验，比较不同样本下t统计量在1%、5%、10%测试水平下的临界值。如果检验t统计值小于临界值，则该时间序列平稳;否则，该时间序列是非平稳的 （周安华，2017）[5] 。从表1中可以看出，德国的DCPI序列的t值大于1%检验水平的临界值，即该一阶差分序列存在单位根，为非平稳时间序列。而美国和中国的t值均小于1%、5%、10%水平下的临界值，且p值均小于0.05，则美国和中国的DCPI序列是平稳的。

一般而言，中国的CPI指数存在春节效应，即在每年春节时CPI指数上涨，存在季节性效应 （查文中，2009）[6] 。为了进一步检验一阶差分后的序列是否存在季节性趋势，绘制DCPI序列的ACF与PACF图，如图2所示。从图2中可以看出，德国与中国的CPI指数存在季节性效应，即当k=12时，一阶差分序列的自相关系数和偏相关系数均显著不为0，印证了序列存在季节性趋势的特点，且周期为12。为了进一步提取序列的季节性趋势，对中国和德国的DCPI序列进行12步季节差分，获得新的时间序列D12CPI。

为了检验季节差分后序列的平稳性，对D12CPI序列进行ADF检验，其结果如表2（见下页）所示。从表2可以看出，中国和德国的ADF检验值均小于1%、5%、10%水平下的临界值（左侧检验），且p值均小于0.05，因此拒绝原假设，即中国和德国的D12CPI是平稳的。

（二）模型识别与定阶

ARIMA模型的识别与定阶是模型构建至关重要的一步（郭晓峰.2012）[7] 。根据平稳性检验可知，对美国的CPI序列选择ARIMA（p，d，q）模型，而对中国和德国采用ARIMA（p，d，q）（P，D，Q）S模型。从图2中可以看出，美国的ACF图和PACF图在1阶截尾，因此美国的ARIMA模型的p和q可以取0、1、2，d=1。

通过对中国和德国的DCPI序列经一阶季节差分之后发现，季节性虽然有所削弱，但并未消除，且进行二阶季节差分并无显著的效果。因此，對该时间序列只进行一阶季节差分，即模型参数D=1。从图3中可以看出，中国和德国的ACF图在0阶截尾，PACF图也在0阶截尾，因此，p=0或1， q=0。本文中对P取0、1或2，Q取0或1。

一般使用Akaike提出的AIC准则和Bayesian提出的BIC准则，即选取AIC与BIC函数值均达到最小的模型为相对最优模型 （Akaike H.1974）[8] 。本文通过对可供选择的模型进行参数估计，发现中国、美国、德国各有4个模型的变量的系数所对应的p值均小于检验水平0.05。通过参数的显著性检验，进而比较这些模型的AIC值和BIC值，其结果如表3所示。从表3中可以看出，其中ARIMA（0， 1， 0）（0， 1， 0）12模型、ARIMA（0， 1， 0）模型、ARIMA（0， 1， 0）（0， 1， 1）12的AIC函数值和BIC函数值均最小。因此，本文选择以上三个模型分别作为中国、美国和德国的最佳拟合模型。

（三）模型检验

模型检验分为两部分。一是模型显著性检验，即检验拟合模型的残差序列是否为白噪声序列。若残差序列为白噪声序列，则说明原始CPI序列的有用信息已经被提取充分，模型显著有效;反之，则需要重新选择模型。二是参数的显著性检验。ARIMA（0， 1， 0）（0， 1， 0）12模型、ARIMA（0， 1， 0）模型、ARIMA（0， 1， 0）（0， 1， 1）12模型通过了参数估计检验，即该模型的参数是显著的。

一般情况下，常用的白噪声检验方法是Q检验。表4（见下页）分别为中国、美国、德国的ARIMA模型的残差序列的Q检验结果，从表中可以看出，Q检验统计量的p值均大于显著性检验水平0.05，因此，可以拒绝原假设，认为该模型的残差序列为白噪声序列，即该模型通过显著性检验。

（四）模型预测与分析

本文选用样本静态预测对中国、美国和德国2020年5月至12月的CPI指数进行预测，其中，2020年5月和6月的CPI用来验证模型的准确性，并对2020年下半年的CPI指数进行预测与分析。图3为三个国家的CPI预测值与实际值的比较，从图中可以看出，模型预测的CPI值与实际值较为接近，且能够捕捉CPI的变化趋势。进一步发现，5月和6月的实际值均在预测的95%置信区间内，CPI在合理的误差范围内波动，表明当前建立的ARIMA模型的预测精度高，能较好地反映各国CPI的规律与趋势。由预测结果可以发现，2020年下半年中国的CPI指数在103.4上下浮动，德国的CPI指数在106.8上下浮动，且由于中国和德国政府的有效控制，CPI有下降的趋势并慢慢趋于稳定;而美国的CPI指数始终呈现出上涨的趋势，表明新冠肺炎疫情的爆发不仅对全球各国经济的平稳运行产生了巨大冲击，造成经济衰退，而且对CPI指数的变化也产生重大影响，使得CPI异常增长。

基于疫情期间各国CPI的变化，可以推测出政府的举措对人民的生活水平产生重要的影响。在应对疫情时，中国政府采取了坚决有力的措施，中国人民对于政府决策的配合度也很高，这使得疫情在中国很快得到有效控制，国民生命财产的损失得到遏制，没有出现大规模的日用品供应短缺、价格上涨，CPI指数没有出现大幅增长。

美国因疫情死亡的人数一路飙升经济增长率下滑，大量民众失业，甚至出现大暴乱。美国的决策者应迅速采取措施来减少伤亡人数，并采取适当的财经政策和货币政策等措施，以保持价格稳定，避免产生严重的通货膨胀。

德国在疫情防控方面也取得了重大进展，在全国范围进一步限制公共活动，遏制新冠肺炎疫情蔓延。除加强疫情防控措施外，还推出大规模经济援助计划，应对疫情对经济造成的冲击，减少疫情对国民的日常生活的影响。

三、结论

本文利用ARIMA模型对各国2000年1月至2020年4月的月度CPI数据建立了具有较高预测精度的ARIMA模型对2020年下半年的CPI数据进行预测与分析，模型预测的相对误差均小于1%。经过检验，该预测模型产生的误差在合理范围内，则用该模型预测2020年的CPI指数具有一定的准确性和参考价值。但是ARIMA模型的短期预测是比较理想的，要从长期预测中获得良好的结果还需要进一步研究。

针对模型预测的结果，政府和国家应该给予重视并积极采取如下措施。（1）发行债券，加大财政补贴力度。（2）适当地进行超前的基础设施建设，例如交通运输、教育、医疗等行业。（3）做好合理的引导，加大国家的调控力度，减少市场的流动性，使物价上涨压力减缓。（4）在防止通货膨胀的同时也要密切关注是否产生通货紧缩等，以此刺激经济的发展，与企业、民众共克时艰。

参考文献：

[1]   雷鹏飞.基于季节性ARIMA模型的中国CPI序列分析与预测[J].统计与决策， 2014，（14）：32-34.

[2]   Mohamed J. Time Series Modeling and Forecasting of Somaliland Consumer Price Index： A Comparison of ARIMA and Regression with

ARIMA Errors[J].American Journal of Theoretical and Applied Statistics， Science Publishing Group，2020，9（4）：143-153.

[3]   Box G E， Jenkins G M， Reinsel G C， et al. Time series analysis： forecasting and control John Wiley & Sons[J].Hoboken，NJ，2008.

[4]   孙颖.基于ARIMA模型的消费者价格指数预测[J].统计与决策，2016，（11）：83-85.

[5]   周安华.分位数单位根检验方法及其应用[D].长沙：湖南师范大学，2017.

[6]   查文中.中国CPI指数的时间序列分析[J].中国集体经济，2009，（27）：71-74.

[7]   郭晓峰.基于ARIMA模型的中国CPI走势预测分析[J].统计与决策，2012，（11）：29-32.

[8]   Akaike H.A new look at the statistical model identification[J].IEEE transactions on automatic control，Ieee，1974，19（6）：716-723.