构造法在高中数学解题中的运用措施探讨

张殷兵

(上海市晋元高级中学 200333)

数学是一门抽象性较强的课程，相较于初中数学，高中数学知识的难度比较大，尤其是在做习题的时候很多学生往往都摸不着头脑，从而出现了无从下笔的情况，甚至有的学生都不知道用哪种方法来解题，随着时间的推移，学生的积极性和自信心会被逐渐打击，学习兴趣也会慢慢降低，直到对数学失去学习兴趣，如果这时再开始进行解题教学为时晚矣，因此，高中数学教师需要从高一开始传授学生不同的解题方法，促进学生解题思路的形成.

一、构造法的概念和运用现状

构造法的形成之日便是数学的诞生之日，也就是说有数学就有构造法，构造法是一种非常实用的解题方法，本质上是指学生构造一个与题干中已知的条件或者是隐藏条件、待求证条件有关系的数学模型，并利用这一模型的性质特点求出题干中的未知.从狭义上来说构造法是一种解题方法，从广义上来说则是一种数学构造思想.在构造法实际应用中，学生首先需要了解构造法的形成和概念，而数学本就是一门抽象的逻辑性学科，如何让学生听懂成为了高中数学教师需要解决的问题.因此，教师需要用通俗易懂的语言为学生讲述，在引导学生通过自己的理解进行构造法解题，在实践中了解和体会，从而真正掌握构造法.

调查发现，现阶段很多高中生虽然已经对构造法产生了一定认知，但是却不懂如何入手，不知道什么题型用构造法，也不知道构造法的运用意义.针对这种情况，教师在日常教学中不仅要为学生讲解构造法，还应该普及其他解题方法，并让学生了解每一种方法的优缺点以及特点，随着时间的积累学生在看到题干时便会很快知道用哪种解题方法，同时也知道构造法在哪种题目中使用.除此之外，教师还需要重视学生联想能力的培养，这样一来学生在看到某一题目时，可以快速捕捉题干信息，与所学的知识建立有效联系，比如解题思路相似？题目已知条件相似？题目未知条件相似？教师通过引导学生联想，可以帮助学生将所学的知识和解题思想进行归纳，从而形成适合自己的数学解题模型，最终实现解题的目的.

二、在高中数学解题中运用构造法的作用

1.有利于提高学生解题能力

构造法既然是数学解题方法，那么对于学生来说掌握了构造法自然可以提高解题能力，尤其是在高中数学中学生要面对复杂的三角函数、指数函数、对数函数等各种数学难题，如何在短时间内获取解题思路成为了解题的关键，而构造法可以帮助学生将未知变为已知，将题干中隐藏的条件变成可视，这样一来可以大大激发学生的解题积极性，甚至可以消除学生对数学的畏难情绪.其实很多高中生的理论知识并不差，只是数学思想和解题思维比较薄弱，这就需要教师在夯实基础的前提下，锻炼学生的解题能力和解题思路，加大训练维度，由此来促进学生对解题方法的熟练.

2.有利于培养学生思维能力

数学是一门对学生思维能力要求比较高的课程，在语文学习中学生只需要会基本的听说读写就可以具备良好语文素质，但是在数学学习过程中，学生需要的不仅仅是口和手，更需要思维意识.学生通过学习构造法，可以形成良好的构造性思维，并在类比、归纳、转化等数学思想影响下实现数学模型的建立，这样一来学生的解题能力、创新能力、构造能力、思维能力都会得到大大提升，同时还可以促进学生数学思维和数学思想的有效统一.

3.有利于培养学生联想能力

在高中数学解题中运用构造法的前提是学生具备联想能力，通过联想才能实现未知和已知的构造转化，而通过构造法解题也可以强化学生的联想能力.因此，在高中数学解题过程中，教师需要注重学生联想能力的培养，首先可以从题目中隐含条件入手，其次从题目类型联想，然后通过联想构造对已有的解题思路和方案进行验证，与此同时教师还需要培养学生的创新能力，联想能力的提升离不开创新能力.

4.有利于学生促进知识转化

高中数学知识点繁多，很多学生在学习时往往都是将每个知识点进行分割学习，却不知很多知识点的内在勾结关系，这样也会导致学生对数学学习完整性缺失.而构造法的运用，可以帮助学生实现相关知识点之间的有效转化，在解题过程中，学生可以用构造法解决几何问题、代数问题、函数问题，这些都可以促进学生对数学知识的转化.

三、构造法在高中数学解题中的运用措施

1.培养学生构造理念

构造法的运用是为了完成解题目标，而解题又是令很多学生头痛的问题，那么在此背景下，教师可以利用学生迫切解题的情绪引入构造法，这可以加深学生对构造法概念的理解，从而逐步形成构造理念.例如在解决难题时，教师可以通过构造法化繁为简，使学生有一种“原来如此简单”的意识.这时教师需要鼓励学生在解题时大胆联想，打破常规将题目简单化.而构造理念不是短时间内可以形成的，需要教师在日常教学中不断渗透，并讲出构造法的优点，让学生在解题过程中灵活运用.尤其是对于一些学习能力差的学生来说，构造法可以帮助他们巩固基础，深入了解不同知识点的含义和相互关系.因此，高中数学教师在构造法教学中要运用层次化教学模式，尊重学生个体化差异，帮助学生突破解题瓶颈，提高数学解题能力，为今后的数学学习打下扎实基础.

2.结合多种解题方法

构造法只是众多数学解题方法之一，也是最有效的解题方法，但是这并不意味着它适合每一道题，其实在数学解题过程中学生需要不断结合多种方法才能实现解题最大效率.例如在解决函数问题时，很多时候都要用到函数极值思想，这时候便不需要再运用构造法，再比如解决方程题目可以运用两边平方法直接解决，掌握构造法的目的是培养学生的联想能力、思维能力、解题能力，而解题能力的培养方法还有很多.所以教师在实际操作中，需要帮助学生掌握多种解题方法，这样才能让学生真正了解构造法的优势，同时在解决问题过程中可以运用多元化解题思路快速解决问题，而不是一味的套用构造法.只有这样才能提高学生的思维能力，从而有效促进数学学习能力的提升.

例如：试证：对任何a>0，b>0，c>0，都有

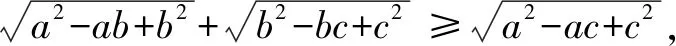
在学生没有学习构造法的时候，解决这道题时一般用三角知识解答，然后直接将两边平方，虽然可以解出答案，但是整个过程比较复杂，而且也不容易说明.相反如果运用余弦定理知识构造三角形，构造三个三角形分别是△ABD、△CBD、△ACD，然后再用余弦定理求出AD、DC、AC，而根据图形知道AD+DC>AC，这样就可以很快证明题目.这样一来学生通过对比分析法、综合法、构造法便会知道构造法的便捷性.

3.积极培养多向思维

在传统数学教学中学生往往是运用固定式思维来解决问题，导致学生的数学解题能力虽然强，但是学生思维能力和实践能力却比较差，在运用构造法时往往都差强人意.因此，高中数学教师在教学活动中应该注重学生多向思维的培养，这样学生在解题过程中就不会局限一隅，而是会充分利用构造法利用已知求出未知.与此同时，教师还需要培养学生的转化思维，在数学学习逆过程中运用数形结合的思想快速找到构造法入手点，从而依此探索出题干中隐藏的关联知识点.例如在解决三角函数问题时，可以运用函数图像结合题干解决问题，这便是数形结合思想在构造法中的运用.由此可见构造法对思维能力要求比较高，所以教师不论是在课堂教学还是习题练习中都应该重视学生多向思维和转化思维的培养，只有这样才能保证构造法的有效运用.

综上所述，在高中数学学习过程中学生的课业比较繁重，为了迎接高考要面对数不尽的题海，在这个过程中学生很容易失去坚持毅力，而构造法的运用可以帮助学生重塑数学学习自信心，也培养了学生的数学思维、数学思想、联想能力、创新能力、解题能力，同时也为学生今后的高阶数学学习打下了坚实基础.