初等数学在数学考研题中的妙用

郑彭丹

(湖南省长沙市中南林业科技大学涉外学院 410004)

一、引言

函数是我们解决实际问题的重要工具，初等数学中我们讨论了一次函数和二次函数的定义、图像和性质等初等数学中的重要知识点.在大学阶段，我们深入地学习微积分这个工具，对函数的讨论也会使用更高级的微积分的工具来进行.那么往往我们的学习思路会固化，比方说对函数性态的讨论，我们马上会想到要去求函数的一阶导数和二阶导数，然后根据定理去判断.事实上，在考试如战场的硕士研究生入学考试当中，如果我们能快速的解出一道题，节约宝贵的时间，不按部就班的使用高等数学中的定理结论，而是另辟蹊径的使用一下初等数学中的方法，也未尝不可.下面我们举几个例子，主要看一下二次函数和一次函数在数学考研题中的妙用.

二、几道数学考研题

例1(2004数学二、三，4分)设f(x)=|x(1-x)|，则( ).

A.x=0是f(x)的极值点，但(0,0)不是曲线y=f(x)的拐点

B.x=0不是f(x)的极值点，但(0,0)是曲线y=f(x)的拐点

C.x=0是f(x)的极值点，(0,0)是曲线y=f(x)的拐点

D.x=0不是f(x)的极值点，(0,0)也不是曲线y=f(x)的拐点

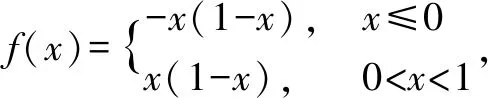
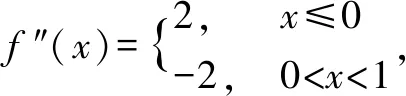
从而当-10,f(x)凹，当1>x>0时，f″(x)<0,f(x)凸，于是(0，0)为拐点.又f(0)=0,x≠0、1时，f(x)>0，从而x=0为极小值点，所以，x=0是极值点，(0，0)是曲线y=f(x)的拐点，故选C.

这道题考察的是分段函数的极值点和拐点情况，按照要求只需要讨论该函数在x=0处f′(x),f″(x)的符号即可.这道题的难点在于函数是一个以绝对值形式给出来的分段函数，求分段函数的导数增加了题目的难度.整个求解过程稍显繁琐，我们可以用二次函数图像快速的把这道题解出来.不难看出函数y=x(1-x)是一个二次函数，而且与x轴相交于(0,0)、(1,0)两点，开口向下，见图1，对函数取绝对值，相当于把图1里的函数图像位于x轴下方的图像做一个对称，位于x轴上方，见图2所示.

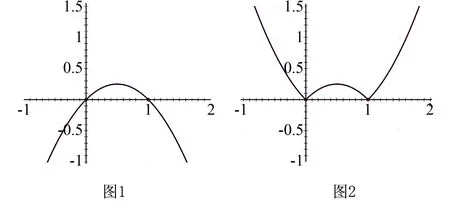
于是我们从图2上很容易判断出在原点处，函数取到极小值，且左右两侧函数图像的凹凸性发生了改变，点(0,0)是拐点.这是一道选择题，不需要具体的解题过程，我们充分利用二次函数及其图像的特点，迅速找到答案.无独有偶，下面的例2也可以做类似的处理.

例2 (2001数学二，3分)曲线y=(x-1)2(x-3)2的拐点个数为( ).

A.0 B.1 C.2 D.3

解法一此道题需要知道拐点的个数，因此我们依然需要对函数求一阶导数和二阶导数，

y′=2(x-1)(x-3)2+2(x-3)(x-1)2

y″=2(x-3)2+4(x-1)(x-3)+4(x-3)(x-1)+2(x-1)2

=2(x-3)2+8(x-1)(x-3)+2(x-1)2

=4(3x2-12x+11)

此时拐点只可能是二阶导数为零的点，我们不妨对函数再求三阶导

y‴=24(x-2)

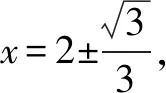
解法一是最常规的一种解题思路，只是计算上颇繁琐，在函数二阶导数的化简上要浪费比较多的时间，另外计算上非常容易出现失误.还有一种解题方法可以避开化简二阶导数，见下面的解法二.

解法二由于本题的函数曲线关于直线x=2对称，所以它要么没有拐点，要么有两个拐点，直接排除选项(B)和(D)，又将y′化简得到y′=4(x-1)(x-2)(x-3)，对导函数y′运用罗尔定理，知道y″有两个零点分别位于区间(1,2)和(2,3)内，且y‴≠0，故y=f(x)有两个拐点.

解法二的关键是对y′进行了变形，从而想到了运用罗尔定理，找到y″的两个零点，而不是直接计算.虽然解法二能成功的避开计算上的繁琐，但是要能想到利用罗尔定理，对学生的数学能力也是要求比较高的.那么还有没有其他的解题思路呢？我们似乎从上面的例1受到一些启发，下面我们来看解法三.

解法三函数y=(x-1)(x-3)是一个二次函数，而且，我们可以大概的知道它的图像如图3所示，对于函数y=(x-1)2(x-3)2的图像，类似例1，我们可以得到|(x-1)(x-3)|的图像，并对其适当放缩即可，大概如图4所示，不难看出，函数y=f(x)有两个拐点.

比较上述三种解法，显然，我们巧妙的使用二次函数图像的特点，非常迅速的而且很简单的就解出了这道题.例1和例2均是利用了二次函数的特点，快速得到选择题的答案.那么，我们稍作总结，例1和例2考察的是函数的性态，可以结合函数图像找出答案，恰巧题目已知函数的图形又可以通过熟知的初等数学中的函数图形来得到，因此，诸如这样的求函数性态的小题题型，当函数图像能够容易得到时我们可以考虑图像法.

例3(2016数学二，4分)设f(x)具有二阶导数，g(x)=f(0)(1-x)+f(1)x，则在区间[0,1]上( ).

A.当f′(x)≥0时，f(x)≥g(x)

B.当f′(x)≥0时，f(x)≤g(x)

C.当f″(x)≥0时，f(x)≥g(x)

D.当f″(x)≥0时，f(x)≤g(x)

解根据题设选项，欲比较f(x)和g(x)的大小，不妨令F(x)=f(x)-g(x)，则F(x)=f(x)-f(0)(1-x)-f(1)x，且F(0)=F(1)=0，对F(x)求导得F″(x)=f″(x)，故当f″(x)≥0时，函数F(x)是凹函数，也即有F(x)≤F(1)=F(0)=0，从而F(x)=f(x)-g(x)≤0，选D.

在上述解答过程中，我们构造辅助函数F(x)，利用F″(x)的符号，判断出函数F(x)的凹凸性，从而找到答案.实际上，这道题中g(x)就是一个一次函数，而且是连接两点(0,f(0))和(1,f(1))的直线方程，当f″(x)≥0时，函数f(x)是凹函数，由凹函数的定义立马有f(x)≤g(x)，于是答案选D.因此，如果熟知一次函数的性质和图像，这道题基本上不需要计算，可以很快找到答案.

三、结论

本文通过分析几道考研数学题，发现初等数学的基础知识在高等数学解题过程也会有妙用.本文着重分析了一次函数和二次函数在考研选择题中的妙用，一来给参加硕士研究生考试的广大考生提供一种解题思路，二来也启发低年级的学生们，无论处在学习的哪个阶段，都需要打好基础，只有基础牢固，才能对数学知识灵活运用，巧妙运用！