空间机械臂精度分析研究与软件实现

王友渔，唐自新，李德伦，曾 磊，张昕蕊，王 念

(1.北京空间飞行器总体设计部空间智能机器人系统技术与应用北京市重点实验室，北京100094；2.北京卫星制造厂，北京100094)

1 引言

空间机械臂是空间站建造、运营、维修及拓展等过程中不可或缺的关键设备，其精度是设计制造需要考虑的重要因素，也是开展高精度动力学与控制技术研究的基础。

最具代表性的空间舱外机械臂是加拿大研制的大型遥操作臂系统(SSRMS)，安装在国际空间站上。根据载人航天任务规划，中国空间站也将配备一个大型七自由度空间站机械臂，目前已完成鉴定产品研制，开展了大量的精度设计、分析与验证工作。当前空间机械臂精度研究主要集中在针对地面机械臂建立位姿误差模型，并进行相关的误差分析上，研究方法具有一定的片面性，分析的误差因素不全面。影响空间机械臂精度的因素很多，如制造及装配的误差、关节间隙误差、控制误差、计算误差等地面机械臂常见误差源，还有环境温度影响等空间机械臂特有误差源。特别是关节作为中国空间站大型空间机械臂的核心部件，采用多级传动系统设计方案，如果采用传统国家标准进行计算，其计算过程十分繁琐复杂，很多参数需要查表，对标准制度的依赖性很强。王栋等在考虑关节误差因素基础上，建立了对误差有综合评价性能的机械臂精度模型。于登云、刘志全等针对大型空间机械臂关节重点研究了关节误差及其柔性变形影响，并应用于机械臂动力学建模及控制。何晓煦等为了提高飞机装配机器人末端定位精度，提出了基于误差相似度的残差补偿方法，实现对机器人的几何参数误差辨识及误差补偿，并完成了试验验证。龚星如、柯振辉等以六自由度串联机器人为实验对象，分别开展了机器人误差因素和误差源的综合分析，并对特定构型的机械臂末端误差进行了试验研究。Adel、Song等针对特种工业机器人精度预估及误差补偿技术开展研究工作，并用于提高机器人控制精度。刘冬雨等开展了七自由度机械臂在轨操作末端误差的尺寸链分析，并利用手眼相机完成机械臂末端维修操作精度标定策略研究及试验验证。然而上述研究均未考虑空间环境及构型影响，不适用于特定构型工况任务的高精度操作预估分析需求。

为了实现空间机械臂在轨不同任务构型工况的快速高效精度分析，本文综合各因素影响，采用综合分析方法进行机械臂精度建模，并根据数学模型编写机械臂精度分析软件，以辅助机械臂精度设计分析并指导工程制造及装配，最后通过实例计算验证所建数学模型与软件的有效性。

2 空间机械臂精度影响因素分析

影响空间机械臂的精度因素主要包括以下4类:

1)参数因素:主要包括制造及装配的误差引起的关节转角输出误差、关节转轴偏差、杆件长度误差以及基座和目标点安装位置误差等；

2)负载因素:包括杆件弹性变形、关节传动刚度等，该部分为动态影响因素，不影响稳态到位精度；

3)计算误差:包括控制计算误差、数据舍入误差等，该部分相对其他误差影响很小；

4)环境因素:包括温度影响，噪声扰动影响等。

根据对系统影响规律分析，上述因素可分为系统误差和随机误差。其中加工制造误差、基座和目标点安装位置误差等属于系统误差，可以通过精测标定手段加以补偿，但是对于关节转角输出误差、关节转轴偏差、控制计算误差以及环境因素影响等随机误差很难消除。

根据上述分析可知，机械臂精度主要由关节转角输出误差，关节转轴误差以及连杆几何误差等构成。其中环境温度影响可以等效分解到上述环节，也可以统一通过整臂热分析计算。

1)各关节的转角输出误差:各个关节的转角输出误差对末端的影响效果与末端端点到关节转轴的垂直距离成正比。由于机械臂关节状态在变化，因此各关节转角的转角输出误差对末端的影响因子也会随着各关节到机械臂末端端点的距离变化而变化。该项影响因子定义为α。

2)各关节的转轴偏差:即旋转连杆除了在垂直于转轴的平面上旋转外，还在过转轴的平面上转动角度。该影响因素也与关节转轴与回转中心与旋转连杆中心线的交点到机械臂末端端点的距离成正比。该项影响因子定义为β。

3)连杆几何误差:主要考虑环境温度影响导致的连杆热变形误差，空间机械臂连杆一般选用碳纤维材料时，该项误差相比关节引起误差可以忽略，但是关节等采用金属材料的需要重点考虑。

关节精度通常包括上面提到的关节转角输出误差和关节转轴偏差，而关节转角输出误差又包括传动误差和回程误差。影响啮合齿轮传动精度即传动误差的因素有:齿轮的刚度、齿轮的制造装配误差。而轮齿的厚度、齿轮副的中心距变化、齿轮副回转中心的平行度误差、轮齿齿向误差、轴承间距和齿廓误差等都会对齿轮副侧隙有影响，另外环境温度也会对齿轮的侧隙产生影响。齿轮的侧隙和单向传动误差组成齿轮的回程误差。这些因素相互之间有耦合作用。

传动系中各级齿轮对输出精度的影响因子与各级齿轮转速和输出转轴转速之比成反比，因此首先考虑的是提高输出轴附近齿轮的转角输出精度。根据齿轮的一般设计方法来选择齿轮的传动精度等级，设计齿轮侧隙的时候要综合考虑到空间环境温度变化影响以及侧隙对齿轮回程误差的影响。

3 空间机械臂精度建模

本文通过机械臂运动学理论并综合概率学知识建立考虑因素全面的空间机械臂精度分析模型。首先采用Denavit-Harterberg(D-H)参数法定义运动学模型中各名义参数关系，然后对运动学方程进行推导和分析，最终得到机械臂运动学模型。

某大型空间站七自由度机械臂全长约为10 m，包括7个关节和2个末端，其运动学参数坐标系关系如图1所示，参数数值参见表1。

图1 机械臂运动学参数坐标系Fig.1 Reference frame ofmanipulator kinematics

表1 某大型空间站机械臂运动学参数Table 1 Kinematic parameters of a large spacemanipulator

其中:θ为第i(i＝1，2，3)关节的关节角(两连杆法线的夹角)；d为两连杆的相对位置；a为两连杆的公法线距离；α为绕X轴由Z轴转到Z轴的偏角；β为绕Y轴由Z轴转到Z轴的偏角。并规定轴线平行关节d为0，轴线非平行关节β为0。

采用D-H参数建模方式建立广义坐标变换矩阵，根据平移和旋转矩阵的先后关系，可以采用Tran(a，0，0)Rot(x，α)Tran(0，0，d)Rot(z，θ)Rot(y，β) 以 及 Rot(z，θ)Tran(0，0，d)Tran(a，0，0)Rot(x，α)Rot(y，β)两种模式的建模方式。本软件保留两种建模方案，在实例计算时采用后者建立的相邻连杆间广义坐标变换矩阵如式(1):

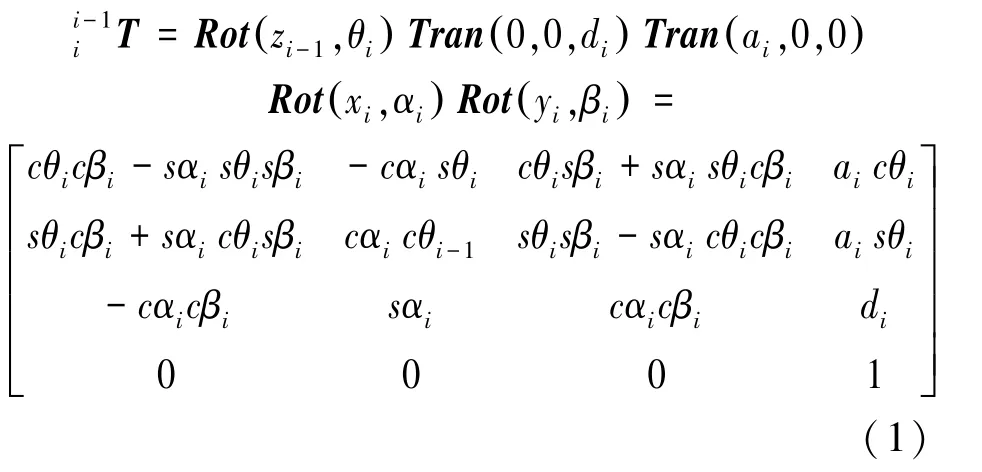
根据机械臂末端误差定义，可得机械臂连杆i相对连杆i-1的误差模型如式(2):

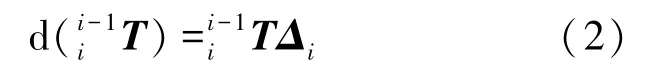
其中Δ为运动学微分变换矩阵，可表示为式(3):

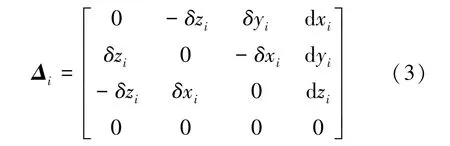
其中d x，d y，d z和δx，δy，δz分别表示连杆i末端的位置和姿态误差。

在实际过程中由于Δθ、Δd、Δa、Δα、Δβ等机械臂各参数误差都很小，可以采用连杆间的微分运动学模型来代替，对坐标变换矩阵进行全微分，代入式(2)和(3)可得式(4):

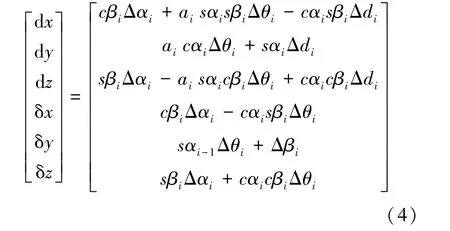
通过累计各连杆误差形成机械臂末端总误差模型如式(7):

4 空间机械臂精度分析

4.1 关节传动误差分析

如果关节齿轮传动装置的组成零部件没有制造和安装误差，在工作时也没有热变形、弹性变形等的影响，那么在关节传动过程中，输入轴转角φ和输出轴转角φ之间应该符合理想的线性关系曲线，即φ和φ之比应该是一个常数，等于总传动链的传动比，即i＝φ/φ。 实际上，各零部件不可能没有制造、装置误差，而且在工作过程中还会产生热变形和弹性变形。因此在传动过程中输出轴的转角难免有误差。

转角误差的角值φ与其在分度圆上的线值Δ之间的转换关系如式(8):

式中，m为模数，z为齿数。本文综合国家标准规定的计算方法，提出基于统计学原理的关节精度计算方法。首先根据齿轮精度影响因素分析，区分出影响关节传动准确性误差的因素，主要包括切向综合偏差、齿距累积偏差、径向跳动、径向综合偏差、公法线长度变动影响因素。然后利用概率统计理论，针对影响传动准确性误差因素进行逐步分析:先计算影响传动准确性的单个齿轮传动误差，重点考虑制造装配误差影响；最后计算整个传动链的传动误差，重点考虑传动过程载荷作用变形影响。通过跳过现有方法中对齿轮副传动误差的计算，避免了定轴轮系中传动副误差累计且不易区分的现象。

基于概率分析齿轮传动误差时，由于传动误差属于随机误差，因此应该先列出传动误差的基本综合式，然后利用概率统计理论，列出传动误差的统计学算式，求出均值和方差，最后通过式(9)所示求出考虑3倍方差的关节传动系统的传动误差。

式中，Δφ为综合转角误差；M(φ)为多次计算转角误差φ的均值；D(φ)为多次计算转角误差φ的方差。

4.2 机械臂整体精度分析

一般来说，给定运动学D-H参数误差值，机器人在不同位姿下，末端的位置误差不同。同样，在同一姿态下，当各个D-H误差参数值在给定范围内变化时，末端位置误差也不同。根据现有机械臂D-H参数模型可以得到机械臂特定姿态特定误差时的末端误差，但是不能给出在机械臂工作空间内，给定关节传动误差范围时的最大误差。

空间机械臂末端误差可以表示为如式(10)、(11)函数:

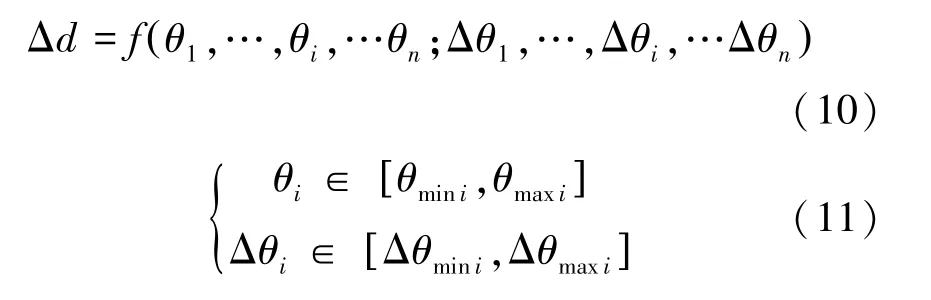
其中θ表示各关节的转角值，Δθ为各关节的 转 角 误 差 大 小。 若 令 x ＝(θ，…，θ，…θ；Δθ，…，Δθ，…Δθ)则可以将机械臂末端最大误差值问题转化为非线性最优化问题，如式(12)所示。

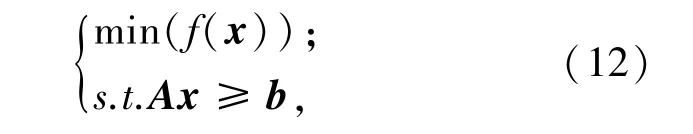
其中A为4n行2n列矩阵，前2n行为单位矩阵，后2n行为单位矩阵乘以-1，b为4n维列向量，前2n个分量分别为θ，…，θ，…，θ，Δθ，…，Δθ，…，Δθ。 后2n个分量为-θ，…，-θ，…，-θ，-Δθ，…，-Δθ，…，-Δθ。

对于该类型的最优化问题可以采用梯度投影法等进行求解。针对空间机械臂工作可靠性及安全性高的特点，本文提出一种求解系统最大末端误差的方法，以保证足够的安全距离。首先按照工作空间要求设置适合的关节角组合，确定机械臂末端姿态，然后在该姿态下搜索误差组合值，使末端姿态最大。关节传动误差对机械臂末端端点位置误差的影响程度取决于末端端点到关节原点或转轴的距离，据此设计适合空间机械臂末端误差搜索算法如下:

如图2所示，θ是第i个关节转角，p是第i＋1个坐标系的原点，d是第i＋1个坐标系的原点到基坐标原点的距离。当第i个关节转角变化时，第i＋1个坐标系原点的轨迹为圆弧。基坐标系原点到圆上点的距离有且只有一个最大值。其距离的变化规律类似正弦函数。用一般的二分法难以找到其最大值。可以考虑先把整个角度变化区间等距离取20个角度值，对每个角度值求第i＋1个关节坐标系原点到基坐标系原点的距离。然后比较这些距离，找到距离最大值对应的关节值。以该关节综合传动误差范围为搜索区间，然后利用三分法搜索距离最大值。

图2 机械臂末端误差搜索算法示意图Fig.2 Diagram of search algorithm for end accuracy error of spacem anipu lator

5 算例分析

空间机械臂精度分析软件由软件界面和分析算法库两部分组成，根据分析层次其界面又分为关节精度分析界面和机械臂系统精度分析界面。用户通过软件界面输入相关设计参数或指标，并点击界面命令按钮，程序就会调用算法库对用户指定类型关节及机械臂进行精度分析。

5.1 关节精度分析

采用齿轮链传动误差分析方法建立的关节精度分析软件框架总体布局如图3所示。

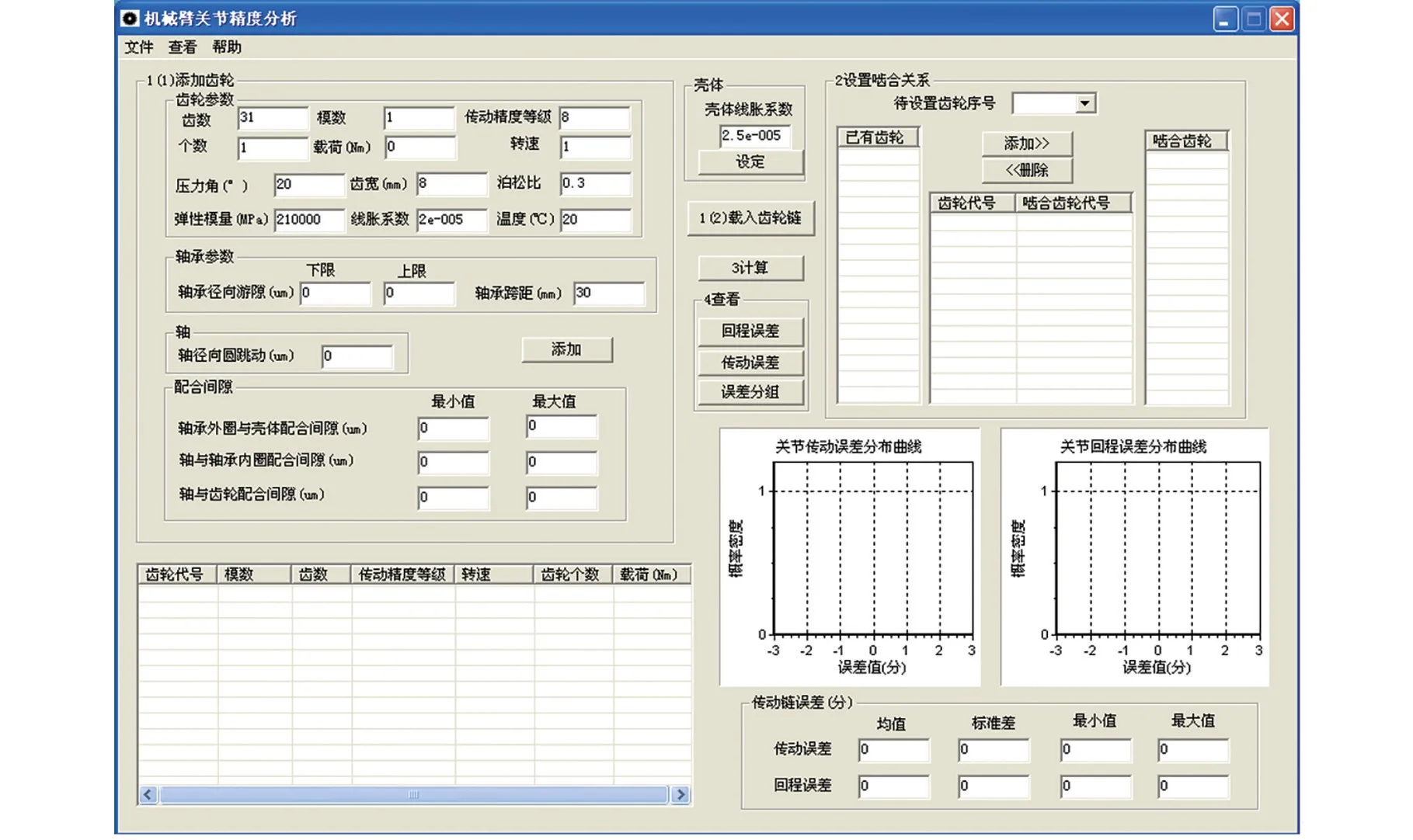
图3 关节精度分析界面Fig.3 Interface of joint accuracy analysis

关节精度分析界面可以分为四大区域:添加关节齿轮区、编辑关节齿轮区、齿轮啮合关系设置区和计算结果显示区。其中个数是指在同一转速级别，具有该类型参数的齿轮的个数；载荷为该齿轮承受的转矩，单位为Nm；配合间隙是考虑到齿轮安装时的装配误差，可以为齿轮孔与齿轮轴的配合间隙，齿轮轴与轴承内圈的配合间隙，轴承内圈与外圈的配合间隙，轴承外圈与壳体的配合间隙，界面中各间隙顺序没有影响；泊松比和弹性模量是齿轮的材料属性；压力角为齿轮分度圆上压力角，默认值为20°。在使用关节精度分析软件过程中，先设置好各编辑框的值，然后单击添加按钮，则可添加相应参数的齿轮到关节齿轮链当中。齿轮添加区域增加的齿轮会在关节齿轮链编辑区域中显示出来。并按照添加顺序设置齿轮代号。

在给定机械臂关节结构参数、材料特性、加工精度及润滑特性等输入条件下，利用本软件的关节精度分析模块进行计算，即可得到关节输出轴的传动误差和回程误差均值，标准差以及最大值和最小值。该大型空间机械臂关节精度分析的软件计算界面及结果参见图4及表2所示。根据分析计算可得关节最大总转角误差约6′。

表2 关节精度计算结果Table 2 Calculated results of joint accuracy

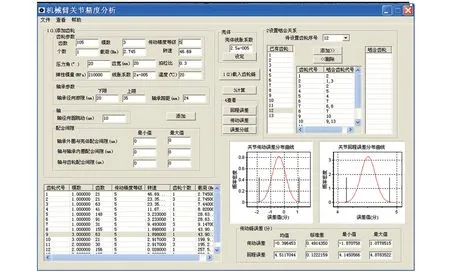
图4 关节精度计算结果Fig.4 Calculated results of joint accuracy

5.2 机械臂精度分析结果

机械臂末端最大误差搜索页面如图5所示。其关节设置区域的主要功能是设置各个关节的转角范围和各项角度误差范围。先选中关节序号下面的一个序号，然后再后面的编辑框中输入相应的数字，点击设定按钮，则设定一组值。之后列表框中会显示各转角范围以及在当前转角范围和转角误差范围状态下使末端位置误差最大的关节转角值以及关节误差值。同时最下面的理论位姿矩阵和实际位姿矩阵也会显示最大误差值时的位姿矩阵，右下角的编辑框中得到最大误差距离预估值。

图5 最大误差搜索界面Fig.5 Interface ofmaximum error search

根据本机械臂精度分析软件进行分析，其中关节转角误差按5.1节的计算结果设置。在关节转角±180°范围约束和关节误差范围约束条件下，基于最大值搜索算法计算分析得到的机械臂系统末端精度结果界面如图6所示，可以得到该大型空间机械臂末端最大位置误差为23.02 mm，对应该七自由度机械臂构型为各关节角度依次为[0°，-180°，90°，0°，90°，180°，-180°]。

图6 机械臂精度计算结果Fig.6 Calculated results ofmanipulator accuracy

已知该机械臂关节及末端外壳材料为铝合金，热膨胀系数23×10/K，温差范围80℃；臂杆材料为碳纤维，热膨胀系数接近0，其变形忽略不计。根据空间环境温度场热变形理论分析计算可知，温度影响导致的等效关节转角误差约0.8′，机械臂末端位置误差约6.5 mm。

因此考虑空间环境情况下，该空间机械臂的末端最大位置误差约为23.02＋6.5＝29.52 mm，能够满足中国空间站任务要求。

5.3 试验验证

按照GB_T20868-2007《工业机器人＋性能规范及其试验方法》标准，采用激光跟踪仪在二维气浮平台对该机械臂工程样机的末端精度进行了测试，如图7所示。通过数据分析确定气浮台测试情况下机械臂工程样机末端位置误差为22.2 mm，与未考虑温度影响前的机械臂末端最大位置误差预估值23.02 mm接近，误差不超过5%，证明了该精度分析方法的可靠性和准确性。

图7 空间机械臂工程样机Fig.7 Prototype of a spacemanipulator

原机械臂的精度设计分析周期需要一周左右时间，现采用该软件可以在2 h内完成分析。因此采用该软件能够快速预估空间机械臂末端精度并应用于实际在轨任务，其计算结果可以作为最大末端误差进行保守预估，从而保证空间机械臂实际运行过程中预留足够的安全距离。

6 结论

本文提出了一种大型空间冗余机械臂精度快速预估分析方法；设计的软件经试验测试，能综合考虑关节输出精度、各关节转轴误差以及环境温度等因素影响，可实现在轨不同任务构型工况的空间机械臂末端精度快速预估，提高空间机械臂精度设计分析效率。