改进PSO优化RBFNN的短时交通流量预测方法

董海 游婷 李小琛

摘要：针对短时交通流的预测精度问题，该文用PSO算法优化RBFNN模型的基础上，引入学习因子优化策略对PSO算法改进，进一步提高预测精度。该文针对PSO算法中认知因子和社会因子在全局搜索和局部搜索的不同作用，对非线性的学习因子做出异步调优改进，通過利用某路段的高速公路监测数据对改进的PSO-RBFNN算法进行训练，获得最优参数值，对短时交通流量进行预测，并将仿真结果与其他模型进行对比分析。实验结果表明，该文改进的PSO-RBFNN模型预测结果稳定，更适用于短时交通流量预测，具有更高的精度。

关键词：粒子群算法（PSO）;神经网络;径向基（RBF）神经网络;交通流量预测

Abstract： Aiming at the prediction accuracy of short-term traffic flow， this paper uses PSO algorithm to optimize RBFNN model， and introduces learning factor optimization strategy to improve PSO algorithm to further improve the prediction accuracy. Aiming at the different roles of cognitive factor and social factor in the global search and local search of PSO algorithm， this paper improves the nonlinear learning factor asynchronously. By using the highway monitoring data of a certain section to train the improved PSO-RBFNN algorithm， the optimal parameters are obtained， and the short-term traffic flow is predicted. The simulation results are compared with other model analysis. The experimental results show that the improved PSO-RBFNN model is stable， more suitable for short-term traffic flow prediction， and has higher accuracy.

Key words： particle swarm optimization; neural network; radial basis function; traffic flow prediction

1 引言

短时交通流量预测是交通控制和交通流诱导的基础和关键，实时精确的交通流量预测对交通管理部门指导资源合理配置，保证交通畅通，提高交通利用效率有重要的意义[1]。针对预测精度问题，近年来国内外专家学者对预测模型均有较丰富的研究。径向基函数神经网络（Radial Basis Function Neural Network，RBFNN）在短时交通优化问题上有明显的优势。RBFNN适用于任意精度的逼近问题，它的核心问题是确定隐含层节点、基函数中心、宽度等参数训练出满足最小误差的神经网络，保证RBFNN的泛化能力。文献[2]利用资源分配法确定RBFNN隐含层节点数，但是依然无法解决陷入局部极值的可能;蚁群算法[3]实现相对复杂，不适用于解决实优化问题。文献[4]将遗传算法（GA）与RBFNN结合，但是GA算法实现步骤复杂，参数多，难以保证参数寻优的稳定性;文献[5]用基本粒子群算法（PSO）与RBFNN相结合，结构简单，易于实现，仍然无法克服陷入局部极值的可能。

为解决以上问题，本文在用PSO算法优化RBFNN的基础上，引入学习因子异步调优策略对PSO算法进行改进，从而达到提高RBFNN预测性能的目的，并将其运用到短时交通流量预测中。

2 RBFNN原理

RBFNN是具有单隐层的三层前馈型神经网络，它通过非线性基函数的线性组合来寻找样本间的线性映射关系，并利用此映射关系实现预测[6]。RBFNN由输入层、隐含层和输出层构成，输入层由信号源节点组成，建立外部输入变量与内部神经元的连接;隐含层对激活函数的参数进行调整，采用非线性优化策略;输出层对线性权进行调整，采用线性优化策略[7]。RBFNN基本结构如图1所示。

RBFNN的预测过程关键在于确定网络的中心和宽度，并训练出隐含层与输出层的线性权值，根据研究目的的不同选取不同的研究方法[9]。

3 PSO算法改进

PSO算法具有的收敛速度快，全局寻优能力强使得其广泛用于神经网络训练、函数优化等方面[10]。然而PSO存在一些不足，容易陷入局部最优、后期种群多样性降低导致“降速”、算法优化结果不稳定等问题[11]。近年来国内外学者提出了各种PSO的改进方案，其中主要集中在参数优化、控制种群多样性等方面。本文基于PSO各种改进经验，从学习因子异步变化方面进行改进。

[α1]和[α2]分别是粒子的认知因子和社会学习因子，认知因子影响着局部搜索性能，社会因子影响着全局搜索性能。学习因子是群体中每一个粒子不断移动到其[pbestti]和[ptg]加速项的权值，选择合适的学习因子有利于算法较快收敛和脱离局部极值。文献[12]研究了一定情况下的非线性关系的学习因子配对[kα1+α2=d]能加速粒子群的优化能力，本文在文献[13]基础上，根据粒子群优化算法收敛定理，增加了非线性的学习因子异步变异操作，在后期非线性增加粒子社会经验减少自身经验，增加局部搜索的性能，达到快速收敛的目的，异步操作如下：

4 仿真实验及相关分析

4.1 实验准备与预处理

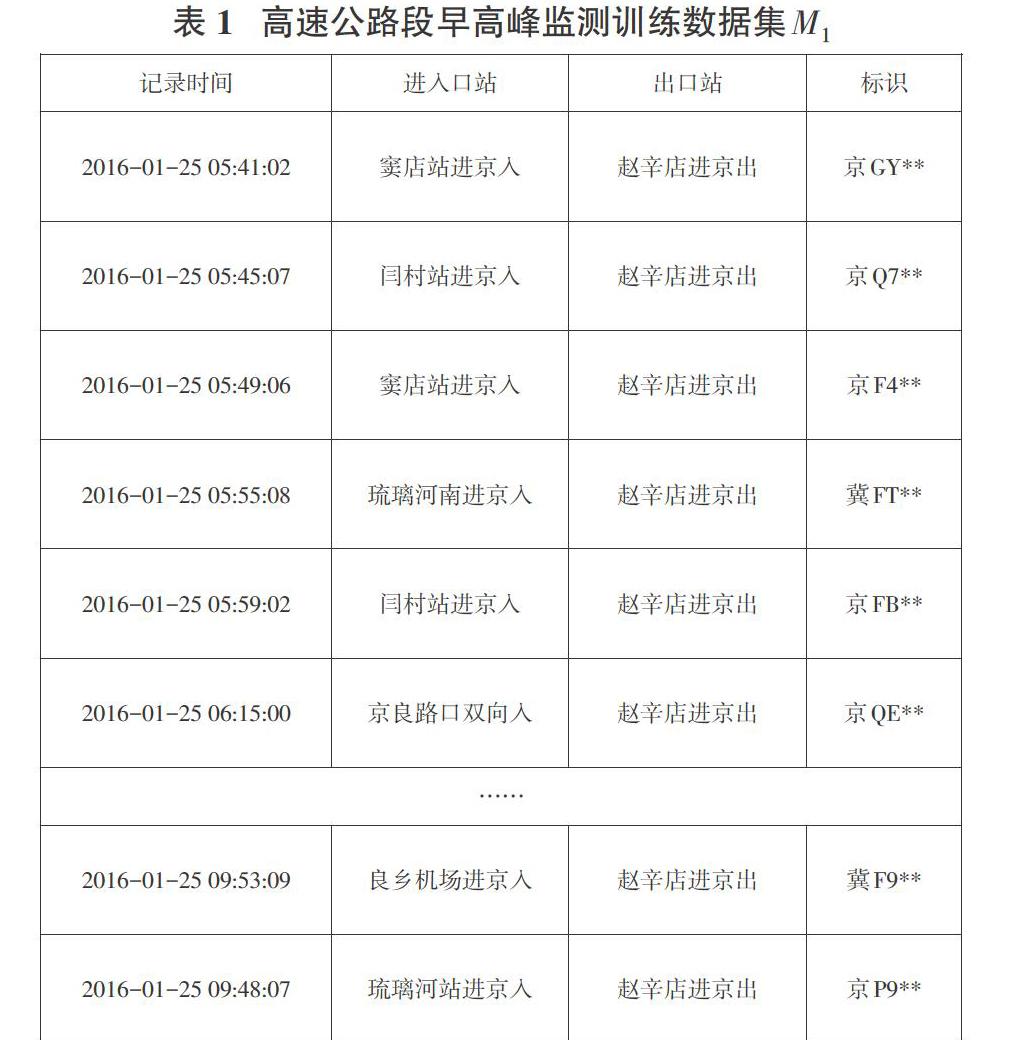
为检验改进PSO优化RBFNN在短时交通流量预测中的性能，使用Matlab 2008a神经网络工具箱进行仿真。选定某路段高速公路监测站的监测数据集进行训练，数据集[M1]见表1。实验主要对标准PSO、改进的PSO、优化RBFNN模型进行对比，从寻优性能和预测精度两个方面进行分析。

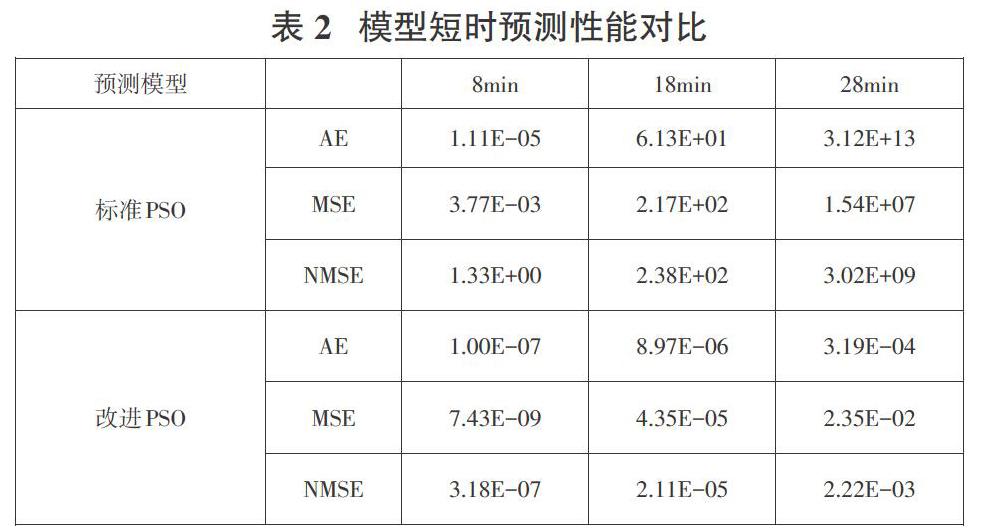
短时交通流量根据预测周期状态可以分为短期和中长期预测，一般将5min-30min的预测作为短时预测，大于30min的预测为长期预测[14]。为了评价改进PSO-RBFNN在短时交通流量预测的能力，利用训练好的模型，分别对不同的训练模型预测，观察模型对8min、18min和28min的各误差函数，具体见表2。

根据表2分析可得，两种模型在8min种的流量预测精度最高，AE、MSE、NMSE的误差都在合理范围内，在28min和18min的流量预测中，精度相对减少，PSO在18min和28min表现稳定性较差，但是相比于改进PSO-RBFNN效果欠佳。相对于本文的短时预测中，在8min的范围内，本文改进的PSO优化RBFNN算法具有更好的性能和精度。

5 结束语

针对短时交通流量预测的问题，本文提出了一种非线性递减的异步学习因子处理策略，该方法充分利用非线性的特点，结合当前种群特点，减少陷入局部极值的可能，提高了算法的求解精度。本文将改进的PSO算法与标准的PSO算法与本文提出的RBFNN优化模型对比，从寻优性能和预测精度两个方面进行对比分析，结果表明，改进PSO-RBFNN寻优性能时间短，精度高，更适用于短时交通流量的预测。

参考文献：

[1] 张军，王远强，朱新山.改进PSO优化神经网络的短时交通流预测[J].计算机工程与应用，2017，53（14）：227-31，45.

[2] 甘文道，周城，宋波.基于RAN-RBF神經网络的网络安全态势预测模型[J].计算机科学，2016，43（S2）：388-92.

[3] 马洪伟.基于蚁群算法的RBF神经网络优化算法[D].青岛大学，2009.

[4] 黄智宇，曹玉恒，基于GA-RBF网络的磷酸铁锂电池SOC预测研究[J].重庆邮电大学学报（自然科学版）， 2013，25（3）：412-7.

[5] XU Q， LIU M. Simulation and Forecast About Vegetable Prices Based on PSO-RBFNN Model， Berlin， Heidelberg， F[C]. Springer Berlin Heidelberg， 2013.

[6] 石东源，熊国江，陈金富，等.基于径向基函数神经网络和模糊积分融合的电网分区故障诊断[J].中国电机工程学报， 2014，34（4）： 562-9.

[7] 周俊武，孙传尧，王福利.径向基函数（RBF）网络的研究及实现 [J].矿冶， 2001（4）：71-5.

[8] 黄文明，徐双双，邓珍荣，等.改进人工蜂群算法优化RBF神经网络的短时交通流预测[J].计算机工程与科学，2016， 38（4）：713-9.

[9] 朱明星，张德龙. RBF网络基函数中心选取算法的研究[J].安徽大学学报（自然科学版）， 2000（1）： 72-8.

[10] 李宁.粒子群优化算法的理论分析与应用研究[D].华中科技大学，2006.

[11] KANUNGO D P， NAIK B， NAYAK J， et al. An Improved PSO Based Back Propagation Learning-MLP （IPSO-BP-MLP） for Classification， New Delhi， F[C]. Springer India，2015.

[12] 毛恒.粒子群优化算法的改进及应用研究[D].华侨大学，2008.

[13] 王磊， 王行甫， 苗付友. 一种带有二维扰动和自适应学习因子的粒子群算法[J]. 小型微型计算机系统， 2018， 39（11）： 2353-7.

[14] HUANG H， LIN M， ZHANG M. A Normalization Method of Converting Online Handwritten Chinese Character  to Stroke- Segment Mesh Glyph， Berlin， Heidelberg， F[C]. Springer Berlin Heidelberg，2012.

【通联编辑：代影】