傅里叶变换的“4+2”教学方法

许 可， 陈沛铂， 王 玲， 邓 彬， 万建伟

(国防科技大学 电子科学学院，湖南 长沙 410073)

0 引言

在电子信息类本科专业中，“数字信号处理”是一门开设在“信号与系统”[4]课程之后的专业基础课程[1～3]。但是在“数字信号处理”课程的教学实践中，我们发现学生往往对前修课程的相关知识点产生了混淆或遗忘，比如学生认为之前已经学过了连续时间傅里叶变换和离散时间傅里叶变换，接下来还会学习离散傅里叶变换，不知道这些“傅里叶”是什么关系？大名鼎鼎的FFT(Fast Fourier Transform)算法，将数字信号处理从理论研究推向了工程实践，那么FFT算法是一种全新的傅里叶变换吗？

为了更好地衔接学科基础课(“信号与系统”)和专业基础课(“数字信号处理”)的相关知识点，我们采取“4+2”教学方法来归纳这两门课程中涉及到的六种傅里叶变换[1,5](如表1所示)。

“4”是指在“信号与系统”课程中学习过的4种傅里叶变换，即CTFS，CTFT，DTFS和DTFT。在时域和频域，这些“傅里叶”或者是连续的，或者是无限长的，因此不方便用计算机或DSP(Digital Signal Processor)直接处理。

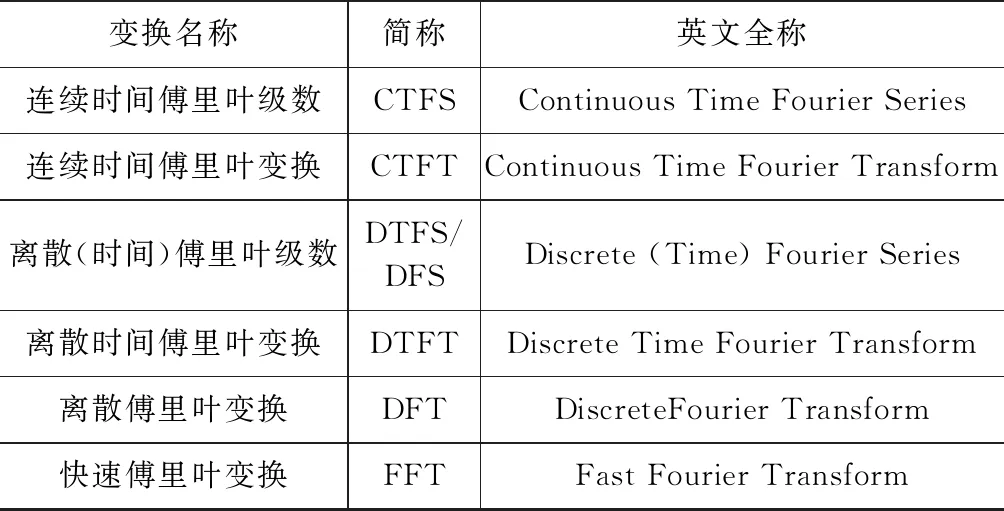
表1 六种傅里叶变换

“2”是指在“数字信号处理”课程中将要学习的2种傅里叶变换，即DFT和FFT。在时域和频域，这两个“傅里叶”都是离散且有限长的，因此可以用计算机或DSP直接处理。

因此，能否通过计算机或DSP直接处理，可以作为划分“信号与系统”与“数字信号处理”这两门课程知识点的一个准则，也是把这六种傅里叶变换划分为“4+2”的原因[1,5]。

在课程教学中还需要特别指出：DFS是DTFS的简称，但DFT不是DTFT的简称，这算一种约定俗成。因此在有的教材中为了同DFT区分开，特意把DTFT称作“离散时间序列的傅里叶变换”[1,2]。

1 “信号与系统”中的“傅里叶”

可以用三角波和周期三角波为讲解对象(见图1)，复习和归纳“信号与系统”课程中讲授的四种傅里叶级数变换。在此的“傅里叶变换”是一种广义的说法，也就是说无论是“傅里叶变换(Fourier Transform)”，还是“傅里叶级数(Fourier Series)”，统称“傅里叶变换”。

图1左侧表示时域，右侧表示频域。在时域，横轴表示从连续时间信号到离散时间信号，两者的转换就是采样；纵轴表示从周期信号到非周期信号，两者的转换就是将周期趋向于无穷大。在频域也有类似的转换关系，需要注意的是，时域和频域的坐标定义与方向是不同的。

为了全面理解图1的内涵，需要深刻理解下面两句话[1,6,7]：

第一句话，傅里叶变换是时域到频域的桥梁。

可以看出这四种傅里叶变换都是从左(时域)到右(频域)的箭头，起到了时域到频域的桥梁作用。反过来，从频域到时域也有桥梁，这就是对应的各种傅里叶反变换。

图1 四种傅里叶变换的关系

第二句话，一个域的离散，对应另外一个域的周期延拓。对于这句话，最耳熟能详的就是时域采样定理中的“时域采样对应频域上的周期延拓”，结合图2，我们还可以更全面的理解这句话：①时域上的离散(采样)，对应频域上的周期延拓，即序列的DTFT和周期序列的DTFS，两者在频域上都呈周期特性。②时域上的连续，对应频域上的非周期，即非周期信号的CTFT和周期信号的CTFS。③时域上的周期，对应频域上的离散，离散的频域取值就称作傅里叶级数，即周期信号的CTFS和周期序列的DTFS。④时域上的非周期，对应频域上的连续，连续的频域取值就称作傅里叶变换，即非周期信号的CTFT和序列的DTFT。

图2 “周期-离散，非周期-连续”的对应关系

2 “数字信号处理”中的“傅里叶”

“数字信号处理”课程中将要学习两种“傅里叶”，分别是DFT和FFT。无论是在时域还是频域，DFT/FFT所处理的信号都是离散且有限长的，这才是能用计算机或DSP直接处理的根本原因。需要特别强调的是：FFT只能算作一种“加速版”的DFT，它不是一种新的傅里叶变换。

对模拟信号经A/D采样并进行截断(加窗)处理，成为有限长的时域离散数据，但在频域其频谱仍然是连续且周期的(DTFT)，计算机或DSP此时仍然不方便直接处理。此时，我们采取“三横两纵”的关系图来理解有限长序列DFT的推导过程[1](见图3)。

“三横”指三种变换关系，即DTFT、DFS和DFT。仍然可用“傅里叶变换是时域到频域的桥梁”，以及“一个域的离散对应另外一个域的周期延拓”这两句话来深刻理解这三种变换关系。并且这三种变换的“进化”过程可以辅助理解DFT的周期特性是如何被“隐藏”起来的。

“两纵”指在时、频两个域同时进行的操作。在时域经过了“均匀采样→周期延拓→取主值序列”操作，对应于在频域进行的“周期延拓→均匀采样→取主值序列”操作。通过DFT变换，从时域的N点样本序列出发，得到频域的N点样本序列。

图3 DFT与其它变换关系示意图(“三横两纵”)

3 结语

在“数字信号处理”课程的教学实践中，通过图表法来总结归纳前后课程知识点，可以起到事半功倍的作用。我们一般在第2次课就会结合图2来复习前修课程的知识点，学生反映他们可以思路清晰、自信满满的开始专业课程的学习。结合图3来讲授DFT，学生不仅可以完整的理解DFT的来龙去脉，而且还更深刻的理解了DFT隐含的周期特性。