Neural-Network-Based Control for Discrete-Time Nonlinear Systems with Input Saturation Under Stochastic Communication Protocol

Xueli Wang, Derui Ding, Senior Member, IEEE, Hongli Dong, Senior Member, IEEE, and Xian-Ming Zhang, Senior Member, IEEE

Abstract—In this paper, an adaptive dynamic programming(ADP) strategy is investigated for discrete-time nonlinear systems with unknown nonlinear dynamics subject to input saturation. To save the communication resources between the controller and the actuators, stochastic communication protocols (SCPs) are adopted to schedule the control signal, and therefore the closed-loop system is essentially a protocol-induced switching system. A neural network (NN)-based identifier with a robust term is exploited for approximating the unknown nonlinear system, and a set of switch-based updating rules with an additional tunable parameter of NN weights are developed with the help of the gradient descent. By virtue of a novel Lyapunov function, a sufficient condition is proposed to achieve the stability of both system identification errors and the update dynamics of NN weights. Then, a value iterative ADP algorithm in an offline way is proposed to solve the optimal control of protocol-induced switching systems with saturation constraints, and the convergence is profoundly discussed in light of mathematical induction. Furthermore, an actor-critic NN scheme is developed to approximate the control law and the proposed performance index function in the framework of ADP, and the stability of the closed-loop system is analyzed in view of the Lyapunov theory.Finally, the numerical simulation results are presented to demonstrate the effectiveness of the proposed control scheme.

I. INTRODUCTION

OPTIMAL control has been one of the main focuses of control fields due to its wide applications in various emerging industrial systems, such as electrical power systems,industrial control systems, and spacecraft attitude control systems [1]–[7]. It is usually equivalent to solve the wellknown Hamilton-Jacobi-Bellman (HJB) equation, which is a critical challenge for nonlinear systems [8]. Fortunately, the adaptive dynamic programming (ADP) algorithm, as the most efficient tool, has been developed to perform various suboptimal control issues with known or unknown system dynamics [9]–[11] by virtue of both its ability of effectively approximating correlation functions and the characteristics of iterative forward transfer. The main idea of ADP algorithms is to utilize two function sequences to iteratively approximate the cost and value functions corresponding to the solution of the HJB equation in a forward-in-time manner [12]. It should be pointed out that the value iteration technology developed in [13], [14] is one of the most important iterative ADP algorithms, and its convergence has also been thoroughly discussed in [15]–[17]. Furthermore, some representative algorithms including heuristic dynamic programming (HDP),dual heuristic dynamic programming (DHP), as well as globalized DHP have been proposed and implemented in various control issues benefiting from the famous actor-critic structure, see [18]–[20]. It is noteworthy that the obtained controller is usually a suboptimal one because of the existence of approximation errors of such a structure, and therefore the corresponding control is also regarded as near-optimal control.

In engineering practice, the actuator saturation is very pervasive due mainly to the facility protection or physical limits of the actuators. If the saturation of the actuator is not considered adequately, the performance of the closed-loop system is often severely damaged [21]. As a result, it is of tremendous significance to survey the influence of the input saturation phenomenon. Under the framework of optimal control, a bounded and invertible one-to-one function in a nonquadratic performance functional is usually exploited to evaluate the cost of saturated inputs and the analytical solution of the optimal controller can be obtained although it is still dependent on the cost functional [8], [22], [23]. Inspired by these work, the near-optimal control for various networked control systems has been investigated and some interesting results have been preliminarily reported in the literature, see[24]–[27], for instance. Near-optimal regulation under the actor-critic framework has been investigated in [26] for discrete-time nonlinear systems subject to quantized effects,where the quantization errors can be eliminated via a dynamic quantizer with adaptive step size. Furthermore, an online policy iteration algorithm has been presented in [28] to learn the optimal solution for a class of unknown constrained-input systems. Obviously, compared with the case without control constraints, the near-optimal control issues subject to constrained-inputs and various network-induced phenomena remain at an infant stage and thus require further research efforts.

On another frontier of research, in the past few years, we have witnessed the persistent development of network technologies, which has been attracting recurring attention on networked control systems [29]. In order to effectively utilize the limited resource or reduce the switching frequency for prolonging the service life of the equipment, only one (or a limited number of) sensor/control node, governed by various protocols, is permitted to get access to the communication network. These protocols include, but not limited to, the round-robin protocol [30], the try-once-discard protocol [31]and the stochastic communication protocol [32], and the event-triggered protocol [33], [34]. There is no doubt that the utilization of these protocols tremendously results in the complexity and the difficulty of both the stability analysis and the design of weight updating rules, which is the main reason why there are sparse results on this topic. Very recently,consensus control with the help of reconstructed dynamics of the local tracking errors has been investigated in [35] for multi-agent systems with event-triggered mechanism and input constraints, where the effect on the local cost from the adopted triggering scheme has been investigated. The critic and actor networks combined with an identifier network have been simultaneously designed in [27] to deal with a constrained-input control issue with unknown drift dynamics and event-triggered communication protocols. Unfortunately,so far, near-optimal control for the discrete-time nonlinear systems subjected to input saturations has not yet been adequately investigated, not to mention the stochastic communication protocol (SCP) is also a concern, which constitutes the motivation of this paper.

The addressed system with unknown nonlinear dynamics is essentially a protocol-induced switching system when SCP is employed to govern the data transmission or update between the controller and the actuator. Usually, SCP can be modeled by a Markov chain and the relative networked control issues can be effectively handled via the switching system theory combined with Lyapunov approaches. It is worth noting that this is a nontrivial topic for optimal control issues due mainly to the challenge of the cost function from such a switch.Recently, two typical approaches have been, respectively,developed in [36] via a combined cost function related to transition probabilities and in [37] via the dynamic programming principle [38]. However, when an identifier is designed to approximate the unknown nonlinear dynamics,there exists a great challenge to disclose the influence on the updating rules of the identifier’s weights and the identification errors. Furthermore, the convergence of the designed ADP algorithm and the practical execution with critic and actor networks should be further inspected. As such, motivated by the above discussions, the focus of this paper is to handle the neural networks (NN)-based near-optimal control problem for a discrete-time nonlinear system subject to constrained-inputs and SCPs. This appears to be nontrivial due to the following essential difficulties: 1) how to design an NN-based identifier under SCPs to estimate system dynamics, 2) how to perform the convergence analysis of the ADP algorithm, and 3) how to disclose the performance of the closed-loop system in the framework of critic and actor networks.

In response to the above discussions, this paper is concerned with the near-optimal control problem for a class of discretetime nonlinear systems with constrained inputs and SCPs, and hence its main contributions are highlighted as follows: 1) an NN-based identifier with a robust term is presented to approximate the unknown nonlinear system, where novel weight updating rules are constructed by virtue of an additional tunable parameter; 2) a set of conditions are derived to check the stability of both identification error dynamics and updated error dynamics of NN weights; 3) the convergence of proposed value iterative ADP algorithm, which solves the optimal control issue of protocol-induced switching systems with saturation constraints in an off-line way, is profoundly discussed in light of mathematical induction; and 4) an actorcritic NN scheme is employed to perform the addressed nearoptimal control issue.

The rest of this paper is formulated as follows: the problem formulation and preliminaries are presented in Section II. For the addressed control issue, four subsections are involved in Section III: an NN-based identification with a robust modification term is designed in Section III-A to identify discrete-time systems with unknown nonlinear dynamics; the value iterative ADP algorithm with convergence analysis is developed in Section III-B; the implementation of ADP algorithm with actor-critic networks in Section III-C, and the performance of closed-loop systems is discussed in Section III-D.Furthermore, a numerical example is given in Section IV to demonstrate the effectiveness of the proposed algorithms.Finally, the conclusion is given in Section V.

II. PROBLEM FORMULATION AND PRELIMINARIES

F ig. 3. State trajectories xk of the open-loop system.

F ig. 4. State trajectories xk of the closed-loop system.

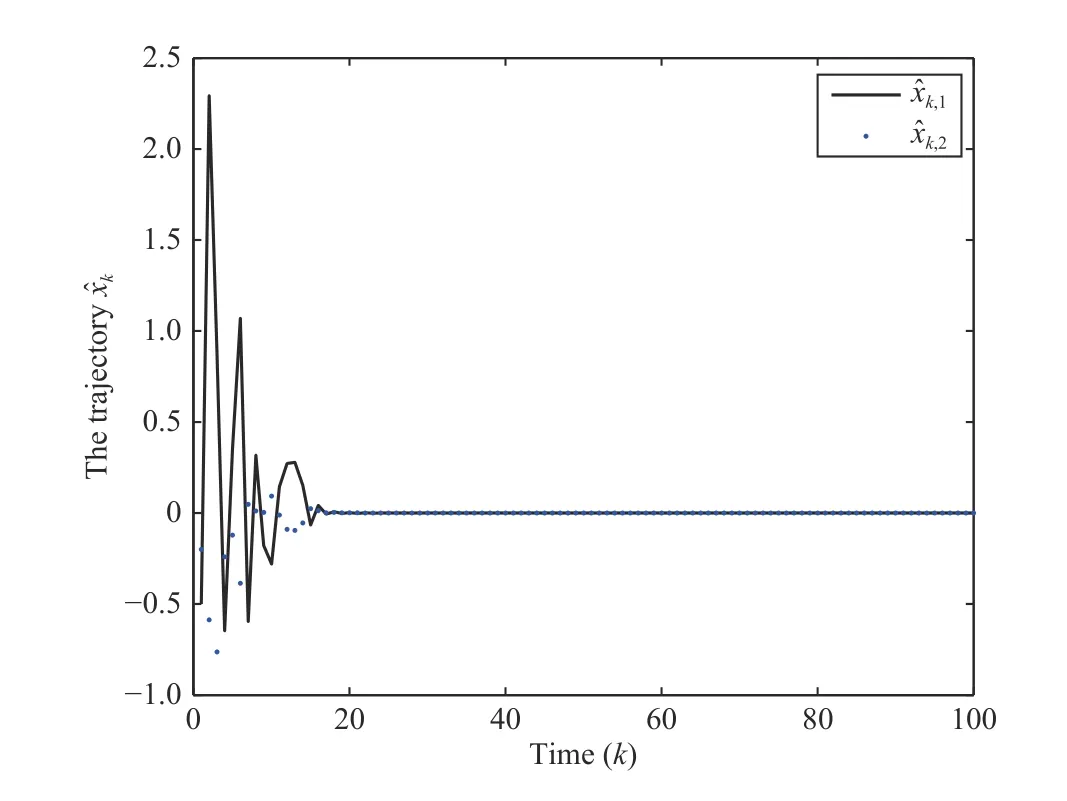
F ig. 5. State trajectories xˆk of the identifer.

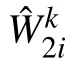
V. CONCLUSIONS

In this paper, we have developed a suboptimal control strategy in the framework of ADP for a class of unknown nonlinear discrete-time systems subject to input constraints.An identification with robust term based on a three-layer neural network in which the weight update relies on protocolinduced jumps, has been established to approximate nonlinear systems and the corresponding stability has been provided.Then, the value iterative ADP algorithm has been developed to solve the suboptimal control problem with boundedness analysis, and the convergence of iterative algorithm, as well as the boundedness of the estimation errors for critic and actor NN weights, has been analyzed. Furthermore, an actor-critic NN scheme has been developed to approximate the control law and the proposed performance index function and the stability of the closed-loop systems have been discussed.Finally, the numerical simulation result has been utilized to demonstrate the effectiveness of the proposed control scheme.