Decoupling Adaptive Sliding Mode Observer Design for Wind Turbines Subject to Simultaneous Faults in Sensors and Actuators
Hamed Habibi, Member, IEEE, Ian Howard, Silvio Simani, Senior Member, IEEE, and Afef Fekih, Senior Member, IEEE
Abstract—This paper proposes an adaptive sliding mode observer (ASMO)-based approach for wind turbines subject to simultaneous faults in sensors and actuators. The proposed approach enables the simultaneous detection of actuator and sensor faults without the need for any redundant hardware components. Additionally, wind speed variations are considered as unknown disturbances, thus eliminating the need for accurate measurement or estimation. The proposed ASMO enables the accurate estimation and reconstruction of the descriptor states and disturbances. The proposed design implements the principle of separation to enable the use of the nominal controller during faulty conditions. Fault tolerance is achieved by implementing a signal correction scheme to recover the nominal behavior. The performance of the proposed approach is validated using a 4.8 MW wind turbine benchmark model subject to various faults.Monte-Carlo analysis is also carried out to further evaluate the reliability and robustness of the proposed approach in the presence of measurement errors. Simplicity, ease of implementation and the decoupling property are among the positive features of the proposed approach.
I. INTRODUCTION
IN recent years, we have witnessed a steady increase in wind energy capacity worldwide, with horizontal-axis wind turbines (HAWTs) being the dominant type of installations.This rapid growth in HAWT installations, however, has led to a growing demand for improved efficiency and reliability[1]–[3]. HAWTs are mainly installed in vastly distributed and remote rural areas and subject to harsh and rapidly changing environments. This makes their maintenance and inspection costly. Moreover, various types of failures in the components are more likely to happen, potentially resulting in costly downtimes [2], [4]. In HAWTs, the most frequent faults occur in the electrical components, including the generator and converter [5], thus affecting the whole operational region.
In the low wind speed region, wind turbines are operated to maximize the captured power by regulating the generator load torque [2]. Hence, when generator faults, i.e., modelled as generator torque bias, occur this objective is not achieved and the HAWT operates with reduced efficiency [5]. On the other hand, in the high wind speed region, HAWTs are typically operated to maintain the generated power at its nominal value,with the least amount of power fluctuations to meet the required power quality of the grid. This is fulfilled by controlling the pitch angle and the generator torque and keeping at the reference values for these signals [2]. This objective will not be fulfilled either when a generator fault happens [6], [7]. In both regions, the generator speed is one of the controller outputs and it is fed back into the nominal controller to compute the corresponding control effort [6].Accordingly, when the generator speed sensor is faulty, the nominal controller is not able to satisfy the objective, even worse, it might lead to HAWT instability and hazardous operation [8], [9].
The HAWT control design has gained significant importance during the last decades. Viable solutions available in the related literature may vary from linear PID [6], linear parameter varying control [7], adaptive nonlinear control [10],optimal control [11], evolutionary algorithms [12], robust control [13], and fuzzy logic systems [14]. However, these solutions fail to operate satisfactorily in the presence of faults.As a result, fault-tolerant control (FTC) is an effective means for improving HAWT reliability and performance and reducing its downtime and maintenance cost [7]. FTCs can maintain satisfactory performance under faulty conditions either using passive approaches that can only mitigate faults that were considered at the design stage, or active ones that require online fault detection and isolation (FDI) followed by control reconfiguration or redesign [2], [8]. Various active FTC approaches have recently been proposed for HAWTs,including observer design [1], [15], fuzzy control [16],adaptive sliding mode control [6], and robust linear parameter varying control [7].
The FDI mechanisms considered in most of these studies have only focused on pitch actuator faults or sensor faults [2],[6], [8]–[10]. Only few works address both sensor and actuator faults, but not simultaneous ones. It is usually assumed that only one type of fault occurred at a time.Therefore, the actuator and sensor simultaneous faults have not been systematically studied. It has only been considered in a few works in which hardware redundancy was required for FDI [2]. Additionally, the estimation of fault type and size is still a challenge for simultaneous faults [17]. Taking into consideration industrial implementation requirements, on the other hand, suggests a simple design with minimum computational cost. Further, it is desirable to keep the nominal controller in use for fault tolerant purposes, thus making observer designs a suitable approach to satisfy this requirement [2], [6]. Another aspect to be taken into consideration is the inaccurate measurement of wind speed, which represents one of the most challenging issues [17]. Even though numerous methodologies have considered the wind speed estimation, such as the non-standard extended Kalman filter[18] and soft computing methodology [19], their practical implementation is quite complicated and ineffective [20].
It should be noted that there are many methods to estimate actuator and sensor signals using observer design such as unknown input observer [21], [22], adaptive robust observer[23], and adaptive sliding mode observer (ASMO) [24]. To highlight the advantages of the proposed method the following remarks are worth noting. In [21] the same fault signal appears in both dynamic modelling and measurement which leads to the availability of extra information about the fault with limited industrial application. Also, it is assumed that the second time derivative of the fault is zero and hence known.More importantly, the stability and convergence of the observer are proven with the assumption of zero initial condition of estimation error. It means that initially there is no estimation error of the observer. In our paper, we have avoided such restrictive assumptions. In [25] the stabilization problem in the presence of external disturbance, actuator degradation and additive sensor fault is studied. Even though this paper follows a similar design approach as ours, the actuator fault is modelled as partial effectiveness loss.However, here we consider a general class of time variable actuator fault. In contrast to [26], we propose the design matrices such that it works for both matched and unmatched actuator faults. Also, for the sake of FTC design as well as for the system monitoring, both sensor and actuator faults are estimated.
On the contrary to [27], [28] the actuator fault is not required to be continuously differentiable, as it is estimated using the so-called concept of equivalent output injection.Generally, in ASMO design several coordinate transformations are required [29]. Also, some optimization approaches,e.g., [30], [31] are used to make the observer dynamic response robust, with suppression of the effect of faults and uncertainties. In this paper, we estimate the system states and faults with neither coordinate transformation nor H∞optimization and the fault effects are actively compensated.More importantly, using the decoupling approach, the ASMO is designed to recover the principle of separation, i.e., the observer dynamics are not perturbed by the control system signal. This offers more design freedom such that the nominal controller can be used in both fault-free and faulty situations.
Motivated by the above considerations, we propose in this paper an ASMO design for HAWTs to estimate the simultaneous generator actuator and sensor faults. In this manner the FDI is achieved, which are necessary for the active FTC purpose. Accordingly, the fault diagnosis task is fulfilled without the need for any redundant hardware component. The final scheme is numerically evaluated on the 4.8 MW HAWT benchmark model. Also, Monte-Carlo analysis is exploited for the evaluation of the reliability and robustness characteristics against the model uncertainty and measurement. Therefore, the main contributions are threefold:
1) A simple design that enables the detection of the generator’s simultaneous sensor and actuator faults, in contrast to most of the studies, e.g., [15], [32], [33], without the need for additional redundant hardware.
2) Compared to some works, such as [1], [5], [7], the proposed approach implements the principle of separation.This enables the use of the nominal controller in faulty conditions. This is achieved by adopting a signal correction scheme to recover the nominal behavior. Another significant feature of this approach is the design freedom, i.e., the nominal controller can be easily replaced by any of the other advanced controllers and no modification is required to the proposed scheme.
3) An easy to implement design in which wind speed variations and aerodynamic torque are considered as unknown disturbances, thus eliminating the need for accurately measuring or estimating them. Moreover, this eliminates the need for computationally-expensive algorithms to estimate the wind speed or aerodynamic torque [5], [8], [10], [12].
The remainder of this paper is organized as follows. In Section II, the HAWT descriptor system is briefly recalled. In Section III, the ASMO is designed with the feasibility and estimation performance analysis. In Section IV, the FTC scheme is designed, using the signal correction approach. The numerical simulation is conducted in Section V. Finally, the conclusions are given in Section VI.
The following notations, which are rather standard, are used throughout this paper. R and C represent real and complex number sets, respectively. ‖•‖ denotes the Euclidean norm of a vector and induced norm of a matrix. Inand 0n×prepresent the unitary matrix of size n, and zero matrix of size n×p,respectively. •†is the Moore-Penrose inverse operator.
It should be noted that to simplify the subsequent notation,if there is no confusion, function arguments are sometimes omitted.
II. HAWT DESCRIPTOR SYSTEM AND PRELIMINARIES
In this section the HAWT benchmark model, detailed in[34], [35] is briefly introduced. The wind kinetic energy is captured by the blades and transferred into the rotor, rotating at ωr. The effective wind speed Vrcauses an induced aerodynamic torque Taand thrust Ft, modelled as
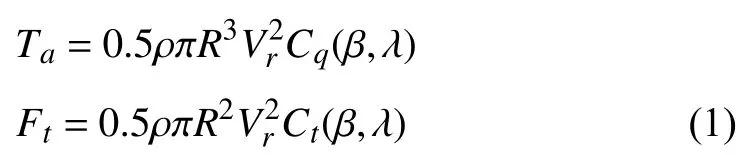
respectively, where ρ is air density and R is blade length.Also, Cqand Ctare torque and thrust coefficients. These coefficients are functions of blade pitch angle, β, and tip speed ratio, λ, defined as λ=Rωr/Vr[2]. Considering the long elastic tower, Tacauses a fore-aft oscillation of the nacelle, i.e., a bending oscillation of the tower. The effective wind speed at the rotor plane is then obtained as Vr=Vw−x˙t,where xtis the nacelle displacement from its equilibrium position, and Vwis the free wind speed, which itself is the wind speed before encountering the blades [10]. It is worth noting that the wind speed measurement by anemometer,installed at the hub, is available on HAWTs. However, due to temporal and spatial distribution of the wind over the blades,tower oscillation, wind shear and tower shadow, there is a significant measurement inaccuracy. So, in this study Vrand consequently Taare assumed to be unknown.
The captured aerodynamic power by the HAWT is as

where Cprepresents the power coefficient. The drive train(DT) is used to increase the rotor speed ωrand transfer the kinetic energy into the generator shaft, rotating at ωg. The DT is modelled as a two-mass system. The rotor and generator shafts have inertia of Jrand Jg, respectively. The elastic gear meshing is considered, with inclusion of the torsion stiffness Kdtand the torsion damping, Bdt. This elastic gear meshing leads to a torsional angle of twist θ∆, defined as,θ∆=θr−θg/Ng, where, θrand θgare the rotation angle of the rotor and generator shafts, respectively. Also, the viscous friction at the bearings of the rotor and generator shafts are modelled with coefficients Brand Bg, respectively. The DT efficiency is ηdt. So, the DT is modelled as [34]


where ag=1/τgand Tgrefers to generator shaft torque. The HAWT internal electronic controller is much faster than the slow mechanical dynamic behavior. Accordingly, the produced electrical power in the generator Pgis approximated as a static relation as

where ηgis the generator efficiency.
As most of the control schemes are designed based on the feedback of the generator speed measurement [2], sensor faults lead to performance degradation or even instability.Lightning, moisture, salt spray and corrosion, may cause sensor faults. Also, if the encoder is used for shaft speed estimation, degradation of metal pieces on the shaft leads to inaccurate speed measurements. Moreover, malfunctions of the electrical components of the encoders represent another reported source of faults [35]. On the other hand, DT resonance frequency content on the generator speed sensor may deviate the sensor output from accurate readings [36].The additive time-variable bias is able to represent a variety of sensor faults, i.e., additive constant bias, multiplicative gain changes in the measurements, fixed and no sensor outputs [2].Therefore, the generator sensor faults are modelled as an additive time-variable bias ∆ωg(t), corrupting the sensor measurement. For the ease of readability, the HAWT model parameters are summarized in Table I.

TABLE I HAWT MODEL PARAMETERS
The HAWT model, can be represented as [2]






which is exactly the nominal behavior, i.e., the fault-free condition of (6). As the stability of the nominal controller is guaranteed, by having the nominal behavior recovered, the stability of the closed-loop system is achieved. ■
Remark 5: Within this structure, the nominal controllers(34) and (35) can be replaced by any of the other modern designs available in the literature. This represents a significant feature of the proposed scheme, since it is based on the decoupling approach. This also gives a design freedom, i.e., a variety of available industrial controllers can be kept in use.
V. SIMULATION
In this section, the performance of the proposed approach is evaluated by implementing it to the 4.8 MW HAWT benchmark, whose technical specifications are illustrated in [7],[34]. It should be noted that the low wind speed case is considered, as the generator sensor and actuator faults have considerable effects. Nevertheless, the proposed solution is applicable for the whole operational region of the HAWT, i.e.,low and high wind speed. The generator sensor and actuator faults are defined as



Also, σ0=1000 , ϵν=1, and τc=0.01. The wind speed profile is shown in Fig.1. Moreover, the generated power with and without the proposed solution are illustrated in Fig.2. It is evident that the effect of the sensor fault is considerable. This is due to the fact that in the nominal control(34) the sensor measurement is squared and multiplied by Kc.In order to accurately compare the results, the approach presented by Shi and Patton in [15] is used as well. The achieved result by applying this approach is shown in Fig.2(black dashed line). It is worth noting that even though in [15]the observer is designed, the robustness is achieved by the H∞optimization approach. More importantly, separate faults were considered. This issue is obvious in Fig.2. Indeed, the approach in [15] satisfactorily suppresses the effects of separate faults. However, when simultaneous faults are applied, this approach performance degrades. In contrast, it is evident that our solution is able to actively compensate for the effects of faults, occurring either separately or simultaneous.
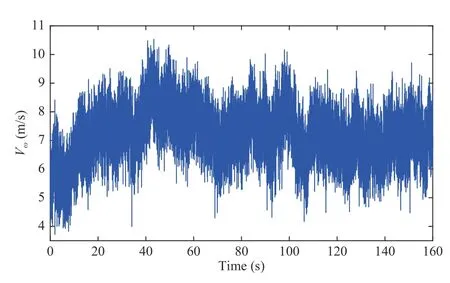
Fig.1. The wind speed profile of the benchmark model.
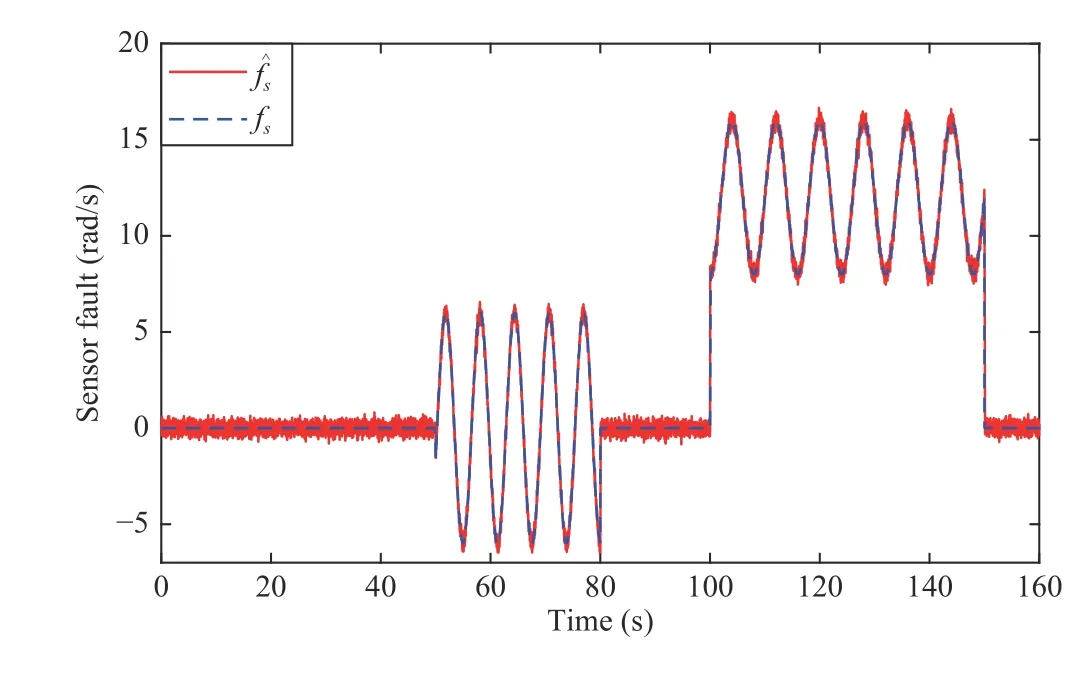
To illustrate the effect of generator actuator faults, in Figs. 3 and 4, the generated power in the time periods 40(s) The estimated sensor and actuator faults are compared to the actual ones in Figs. 5 and 6, respectively. It can be seen that the nominal operation of the HAWT benchmark is recovered using the proposed approach. Moreover, the sensor and actuator faults are accurately estimated. To precisely investigate the effectiveness of the proposed FTC, Tg,refis illustrated in Fig.7. It can be noted that in the faulty periods the Tg,refis corrected corresponding to the estimated faults to remove their effects.normalized power metric (PM) is computed as Fig.2. The generated power in fault-free and faulty conditions, with and without FTC. Fig.3. The generated power in 4 0(s) Fig.4. The generated power in 9 0(s) Fig.5. Actual and estimated sensor fault of fs. Fig.6. Actual and estimated actuator fault of fa. Fig.7. The generator reference torque. where Pg,ffis the generated power in the fault-free condition.Then, the maximum, minimum, mean and standard deviation of the PM is computed. For the sake of brevity, the worst (W),the average (A), and the best (B) values are summarized in Table II. All results presented in Table II show small values of the PM, i.e., limited variation of the generated power in the faulty case with respect to the corresponding one in the faultfree situation. Moreover, Table II highlights the robustness of the proposed approach with respect to measurement errors,wind speed variations as well as faults. It is worth noting that the variations of PM are smaller than the variations of the noise within the considered data sets (S et1, S et2, and S et3). TABLE II MONTE-CARLO SIMULATION RESULTS In this paper, an adaptive sliding mode observer was designed, enabling the estimation of generator actuator and sensor simultaneous faults. As the principle of separation was recovered by the proposed scheme, the nominal controller was kept in use for the fault tolerance purpose, recovering the nominal behavior of the wind turbine in the presence of faults.The accurate measurement or estimation of the unknown wind speed and consequent unknown aerodynamic torque was not required. This led to a simple and less computationallyexpensive scheme which can be used in industry. The effectiveness of the proposed scheme was numerically evaluated using a 4.8 MW wind turbine benchmark model.The reliability and robustness characteristics of the proposed approach against measurement errors were further assessed using the Monte-Carlo analysis. The results showed that the nominal operation was recovered using the proposed approach, in the presence of simultaneous faults and the unknown wind speed variations. Sensor and actuator faults were also accurately estimated using the proposed observer.The contributions of this paper can motivate the following future research directions. For instance, a necessary step to the industrial deployment of the proposed scheme is its experimental validation, with cost analysis and assessment of the economic benefits. This includes the analysis of other faults, the computation of the downtime/availability, and operation costs. This, cumulatively, leads to estimation of the average wind turbine lifespan. On the other hand, the proposed approach can further be extended to the high wind speed region, where the pitch actuator is active. Finally,further Monte-Carlo analysis can be performed to assess other performance metrics, such as false alarm rates, missed fault rates and detection delays.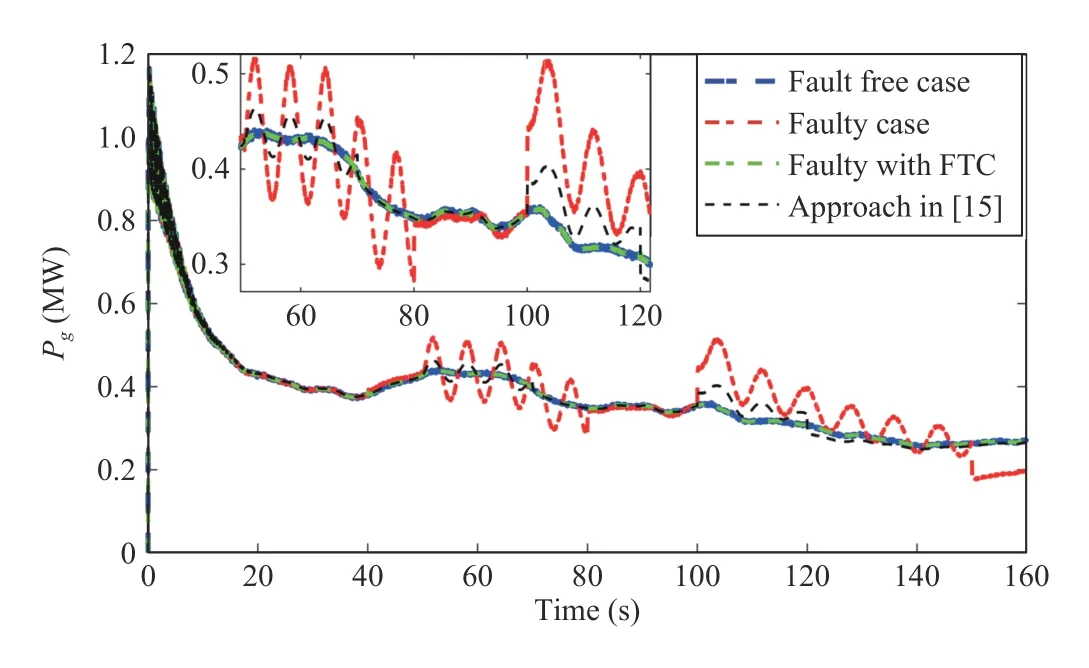





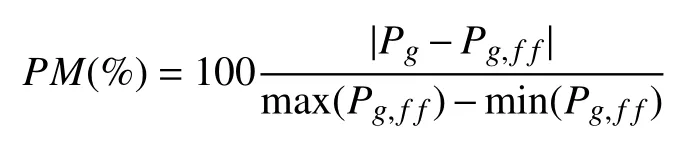

VI. CONCLUSIONS AND FUTURE RESEARCH DIRECTIONS
 IEEE/CAA Journal of Automatica Sinica2021年4期
IEEE/CAA Journal of Automatica Sinica2021年4期
