基于单神经元神经网络的无刷直流电机控制系统仿真

尹洪桥, 易文俊*, 贾 芳, 李璀璀, 王康健

(1.南京理工大学瞬态物理国家重点实验室， 南京 210094； 2.中国兵器工业集团第304厂， 长治 046012)

随着电力电子技术、计算机技术、控制理论技术及传感器技术的飞速发展与应用，无刷直流电机(brushless direct current motor, BLDCM)由于其结构简单、低噪声、出力大和良好的调速性能，广泛应用在电力自动化、工业、军事、航空航天以及家用电器等行业[1-3]。无刷直流电机是指具有串励直流电机启动特性和并励直流电机调速特性的梯形波/方波直流电机，其基本结构由电机本体、功率驱动电路及位置传感器三者组成[4-5]。高性能的控制驱动器是无刷直流电机稳定运行的基础，驱动系统不仅需要快速的响应速度，而且当电机参数变化或者受到外部干扰时能够具有更快的跟踪能力。传统比例积分微分(proportional integral differential，PID)控制算法以其结构简单、出力大、可靠性高以及易于工程实现等优点至今仍被广泛采用，但是该算法对于电机状态的估计是基于线性模型，无刷直流电机是一个多变量、强耦合的非线性复杂系统，如电枢反应的非线性、转动惯量和相电阻的变化等，使得难以用一个精确的数学表达式来描述无刷直流电机的电磁关系，所以采用常规的线性控制方法很难达到理想的控制效果[6]。因此，这就激发了众多专家学者利用各种控制理论来处理非线性工业过程。

20世纪80年代以来，在仿生学进步的基础上，控制领域提出了许多智能控制算法对无刷直流电机进行优化控制。其中有模糊控制[7-8]、滑膜变结构控制[9-10]、模型参考自适应控制[11-12]、蚁群算法[13]、粒子群优化算法[14]、鲁棒控制[15]、遗传算法[16]等，但以上方法分别存在着结构复杂、调节困难、随动性差或者响应迟滞等缺点，在电机控制方面的应用性能还有待进一步改进。在诸多智能控制策略中，由于神经网络控制具有较强的非线性拟合能力，能够通过自适应学习来映射任意的复杂非线性关系，此外其学习规则简单，参数整定方便，具有较强的自学习和鲁棒性，便于计算机编程实现，因此被广泛应用在各类非线性控制系统中[17]。

单神经元神经网络是一种结构简单、易于实现的神经网络，并且可以实现自学习和自适应。随着现代工业现场被控对象的复杂性及其随时间变化的特征，单神经元神经网络PID控制的应用越来越广泛。尤向阳[18]运用单神经元自适应PID控制策略，对超声马达速度响应特性进行了实验研究，结果表明运用该算法能够有效地提高超声速马达转速跟踪控制的动静态性能。蒋林等[19]提出了一种基于模糊单神经元PID控制策略，并应用于改善四旋翼系统的控制性能，最后验证了所设计的控制策略具有较强的自适应性和鲁棒性。王宁等[20]研究了一种改进的单神经元PID控制算法，该算法在神经元算法的加权系数中引入了二次型性能指标，并应用于电厂锅炉过热气温控制，最终结果表明这种控制算法具有优良的控制性能。聂松林等[21]结合传统PID控制提出了一种单神经元PID+前馈控制算法，通过对直驱泵控制系统进行建模仿真，验证了该控制算法的可行性，再一次证明了单神经元神经网络PID控制在实践中的广阔应用前景。现建立无刷直流电机的数学模型，搭建无刷直流电机的转速与电流双闭环控制系统，在转速环中引入基于单神经元神经网络PID算法，并且与传统PID控制算法进行对比分析。

1 无刷直流电机的数学模型

无刷直流电机分别有三个定子绕组和永磁体转子，电机定子绕组为Y接集中整距绕组，转子采用隐极内转子结构，3个霍尔元件在空间相隔120°对称放置。由于磁铁和不锈钢护套都具有高电阻率，因此可以忽略转子感应电流，无需对阻尼器绕组进行建模。因此，在相位变量中三相绕组的电路方程如式(1)所示。

(1)

式(1)中：UA、UB和UC分别为三相绕组相电压；R为三相绕组相电阻，这里假设三相对称绕组中电阻均相等；iA、iB和iC分别为三相相电流；LA、LB和LC分别为三相绕组自感；LAB、LAC、LBA、LBC、LCA和LCB分别为三相绕组之间的互感；d/dt为微分算子，eA、eB和eC分别为三相绕组的反电动势。

由于三相定子绕组结构对称，每相绕组的自感相等，相绕组之间的互感也相等，因此可得LA=LB=LC=L，LAB=LAC=LBA=LBC=LCA=LCB=M。其中，L为三相绕组的自感；M为三相绕组之间的互感，因此有

(2)

其中：

iA+iB+iC=0

(3)

因此

MiA+MiB+MiC=0

(4)

故无刷直流电机相电压方程的矩阵形式可表示为

(5)

电机的电磁转矩方程为

Te=(eAiA+eBiB+eCiC)/Ω

(6)

式(6)中：Te为电磁转矩；Ω为电机机械角速度。

电机的运动方程为

(7)

式(7)中：TL为负载转矩；J为转子转动惯量；Bv为黏滞摩擦因数。因此式(5)～式(7)共同构成了无刷直流电机的微分方程数学模型。无刷直流电机的全桥控制电路拓扑图如图1所示。

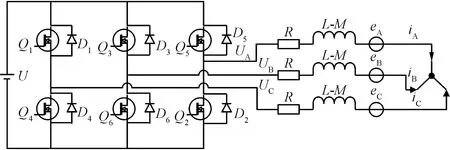
U为直流供电电源，Q1～Q6为金属-氧化物半导体场效应晶体管，D1～D6为续流二极管图1 无刷直流电机全桥控制电路拓扑Fig.1 Full bridge control circuit topology of BLDCM

2 传统PID控制器的原理

在控制系统中，PID控制是最早发展起来的一种控制算法，其优点是算法简单、适应性好、可靠性高。PID控制是一种线性控制方法，数学原理基于调节给定参考输入值yd(t)与实际反馈值y(t)之间的偏差e(t)。PID算法的数学表达为

e(t)=yd(t)-y(t)

(8)

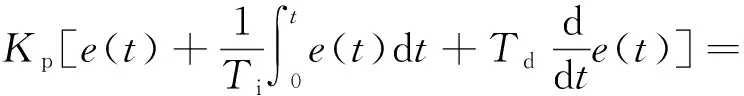
(9)

式中：u(t)为PID控制器的输出值；Kp为比例系数；Ti为积分时间常数；Ki为积分系数，Ki=Kp/Ti；Td为微分时间常数，Kd为微分系数，Kd=KpTd。

PID参数整定必须考虑Kp、Ki和Kd三个参数在不同时刻的作用以及它们之间的相互联系。随着科学领域的不断拓展，利用常规的控制算法难以达到理想的控制效果，采用单神经元神经网络PID控制算法可以把传统PID控制和神经网络控制策略结合起来，该方法克服了传统PID控制器难以进行在线参数整定的不足，实现了对无刷直流电机的有效控制。

3 单神经元神经网络PID控制器的原理

单神经元PID控制器实质上是将比例、积分、微分作为神经元的输入权值，同时将网络中的隐含层简化到一层的变系数、复合、自适应神经网络控制器。它既具有神经网络自学习、自适应能力强的优点，又具有PID控制结构简单、可靠性高、易于工程实现的优点。

单神经元自适应控制器是通过加权系数的调整来实现自适应、自组织功能，权系数的调整是按有监督的Hebb学习规则实现，单神经元神经网络PID控制算法的结构如图2所示。

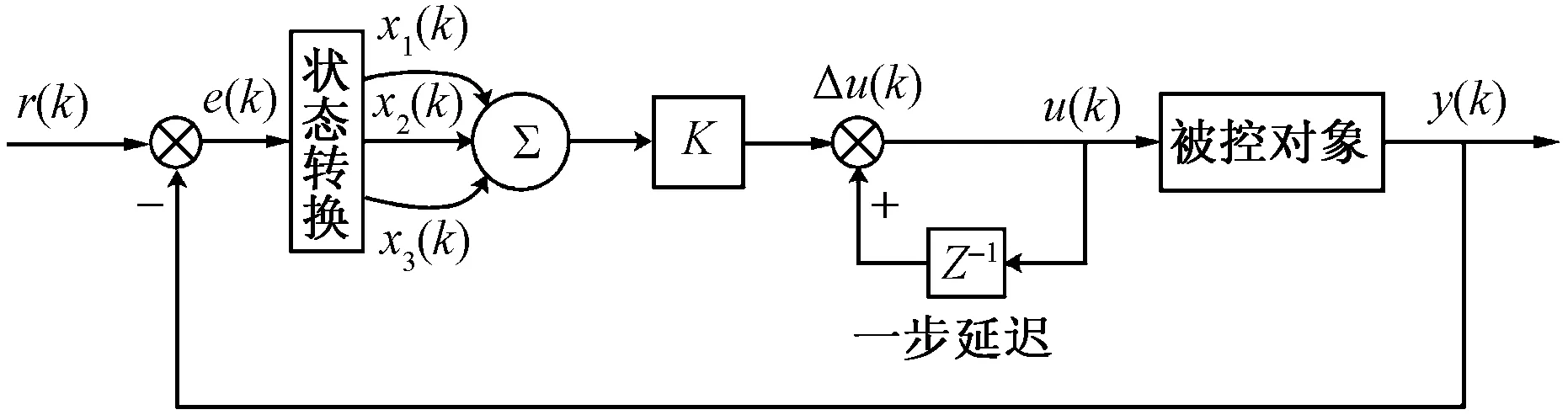
图2 单神经元神经网络PID控制器原理图Fig.2 Schematic diagram of single neuron neural network PID controller

输出值u(k)的计算公式为

(10)

式(10)中：u(k)为控制器输出值；u(k-1)为前一个采样时刻的输出值；K为神经元的比例系数；ω′i(k)为归一化权值；k为系统的每个采样点；xi(k)为误差e(k)的状态转换值，其计算公式为

(11)

式(11)中：e(k)为当前时刻系统输入与输出之间的差值；e(k-1)为前一个采样时刻的差值；e(k-2)为前两个采样时刻的差值。在式(10)中，归一化权值ω′i(k)的计算公式为

(12)

其中3个归一化权值ω1(k)、ω2(k)和ω3(k)的更新规则为

(13)

式(13)中：z(k)为性能指标或递进信号，取z(k)=e(k)；ηp、ηi和ηd分别为比例、积分和微分的学习速率。其中上述公式中神经元的比例系数K取值为1.5，归一化权值ω1(k)、ω2(k)和ω3(k)的初始设定值均为0.01。

对于比例、积分和微分系数分别采用不同的学习速率ηp、ηi和ηd以便对不同的权系数进行调整。调整规则如下。

(1)若系统响应过渡时间太长，则增大ηp、ηd；若超调迅速下降至稳定值而后升值且稳态时间过长，可以减少积分作用；对于大延时系统为了减少超调，ηp、ηd可以适当大些；若系统过渡时间太长，可以适当增大ηi。

(2)K(K>0)为神经元的比例系数，K的选择非常重要。K越大，则快速性越好，但超调量大，甚至可能使系统不稳定；当被控对象时延增大时，K必须减小，以保证系统稳定。K选择过小，会使系统的快速性变差。

4 结果讨论

建立了无刷直流电机的双闭环控制系统，其中电流环采用三相比例积分(proportional integral，PI)控制算法并且设定限流值[0,1]，在转速环中引入了单神经元神经网络PID算法。实验研究所选择的无刷直流电机参数如表1所示。

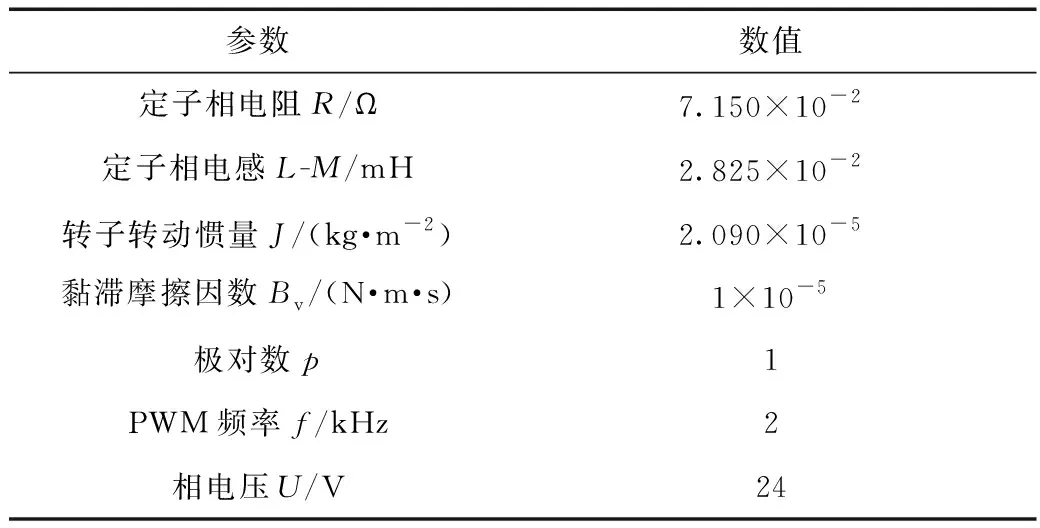
表1 无刷直流电机参数Table 1 Parameters of BLDCM

电机空载条件下全速转动的转速响应曲线如图3(a)所示，其空载转速为8 670 r/min。图3(b)为同条件下A相电流响应曲线图，空载电流为897 mA。

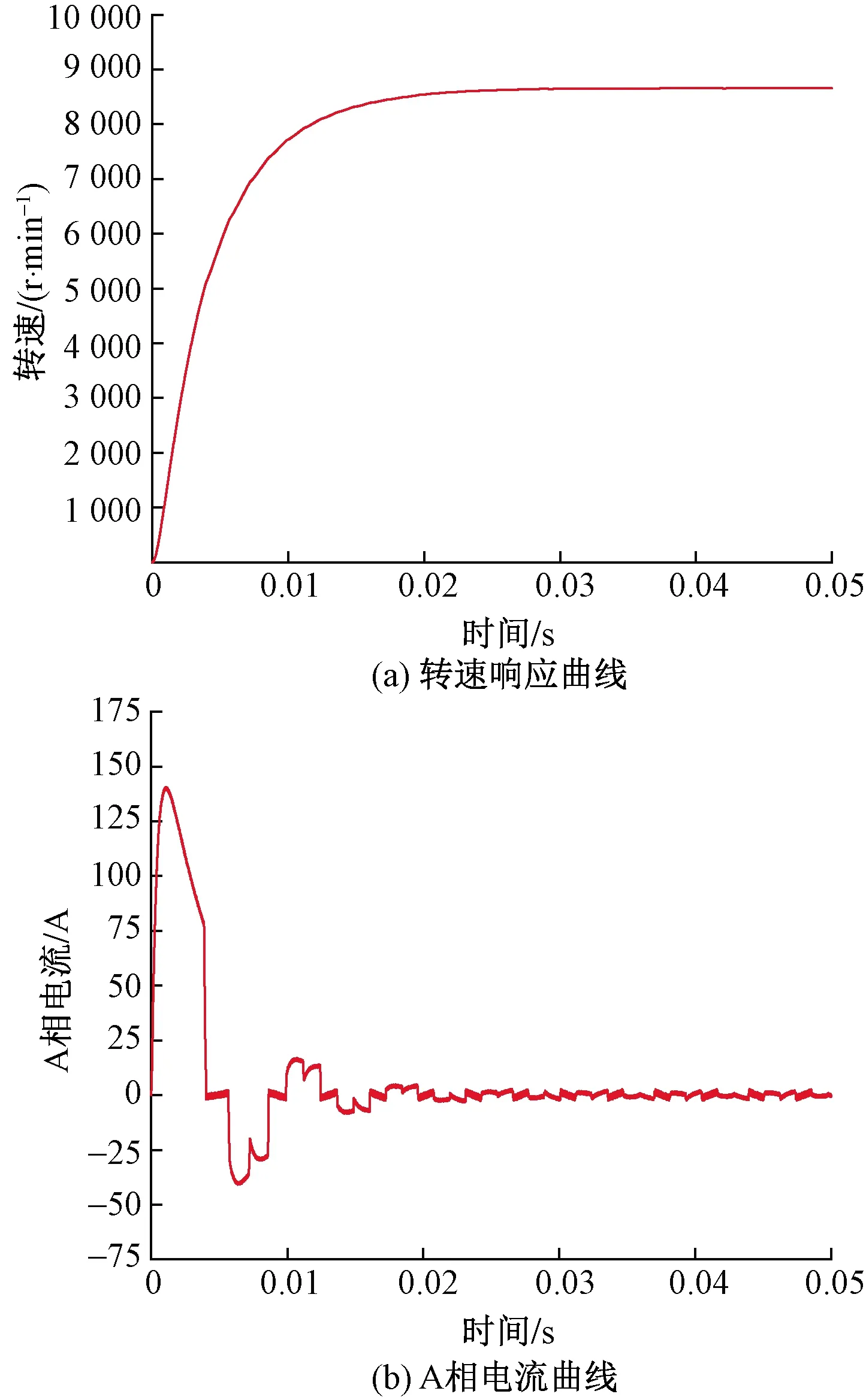
图3 电机空载条件下转速与A相电流响应曲线Fig.3 Response curve of motor speed and phase A current without load

图4为电机空载条件下设定参考转速值为7 000 r/min，转速环分别采用单神经元神经网络PID与传统PID算法控制下的转速阶跃函数响应曲线，并且在表2中比较分析了不同控制算法下系统响应的动态参数性能。从图4和表2可以得出采用单神经元神经网络PID算法相对于传统PID算法，其阶跃函数响应的上升时间和调节时间更短，稳态误差更小，两种控制算法均无超调量。传统PID控制下的电机在转速达到稳定后仍存在较大的转速波动，而采用单神经元PID算法控制下的电机其转速更贴近于参考设定值，且转速波动较小。

图4 空载条件下转速响应曲线Fig.4 Speed response curve without load

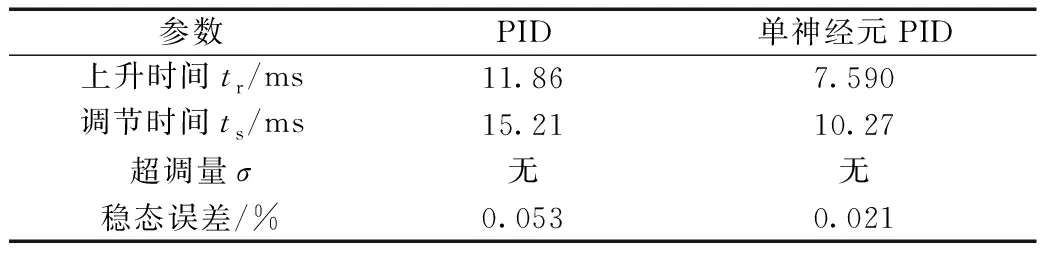
表2 转速阶跃响应动态参数性能对比分析Table 2 Comparative analysis of dynamic parameters of speed response

图5为电机空载条件下分别采用单神经元神经网络PID算法与传统PID算法控制下A、B和C三相电流响应曲线图。从图5可以看出，单神经元神经网络PID算法控制下的电机其电流具有较快的响应时间，能够以更快的速度达到稳定运行状态，无电流波动现象产生，且运行状态相比于传统PID控制更加稳定。

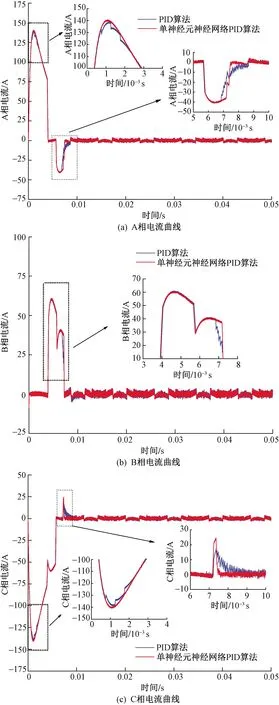
图5 A、 B和C三相电流响应曲线Fig.5 Phase A, B and C current response curve

图6为对比分析不同控制算法下电磁转矩Te的响应曲线图。从图6可以看出，采用单神经元神经网络PID控制算法其响应速度更快，运行状态更加稳定。

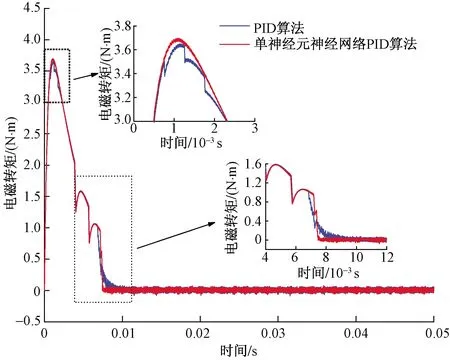
图6 电磁转矩Te响应曲线Fig.6 Electromagnetic torque Te response curve

图7为无刷直流电机控制系统中，转速环分别采用单神经元神经网络PID算法与传统PID算法控制下的A、 B和C三相反电动势曲线图。

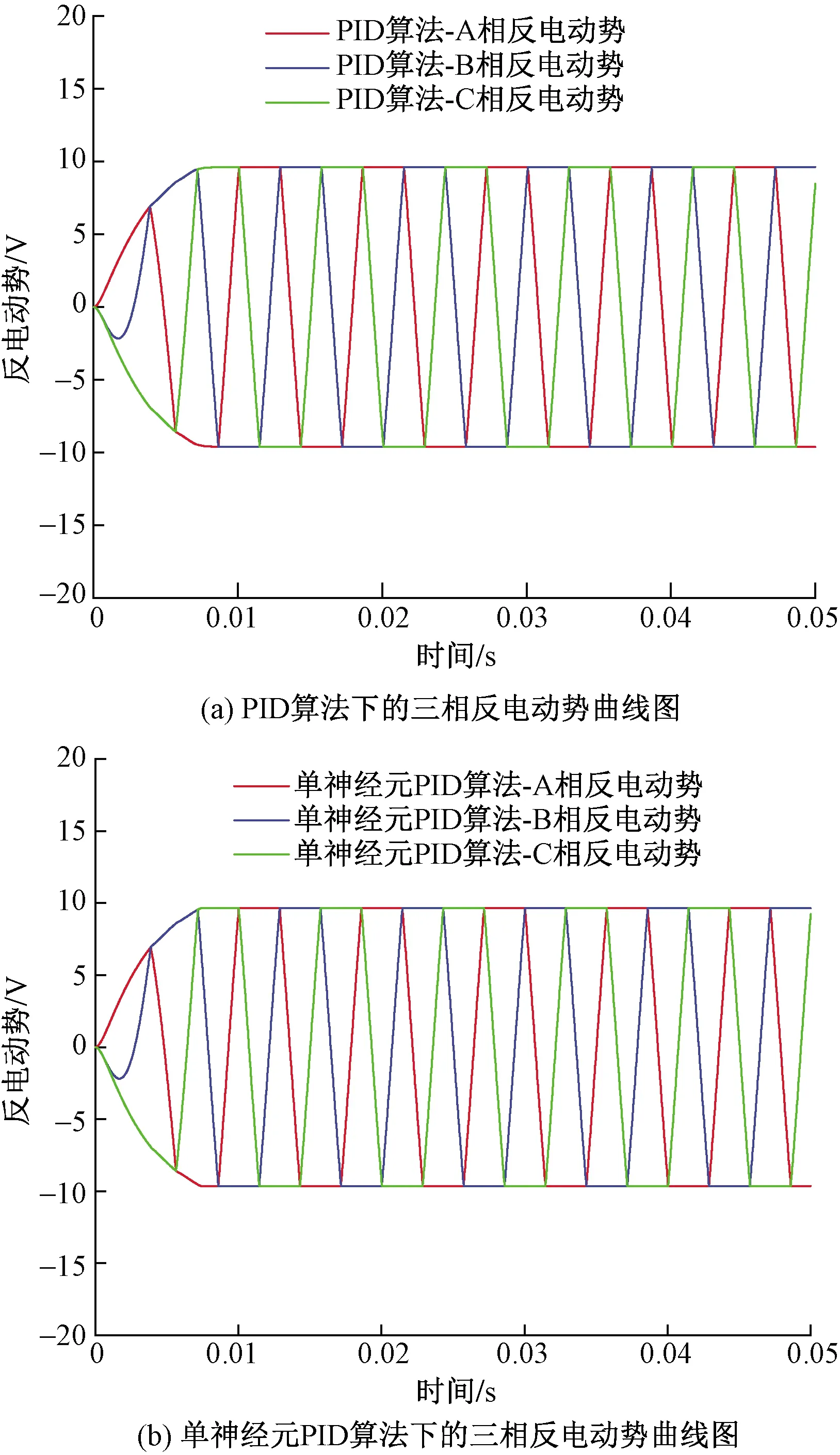
图7 不同控制算法下A、 B和C三相反电动势曲线图Fig.7 Phase A, B and C back electromotive force curves under different control algorithms

从上述分析可以得出，电机刚启动时转速和反电动势均为零，启动瞬间电枢电流迅速增大，使电磁转矩较负载转矩大很多，转速迅速增加；转速增加引起反电动势增大，电枢电流增长变缓直至达到极大值，然后开始减小。电流减小导致电磁转矩减小，于是转速上升的加速度变小。当电磁转矩和负载转矩达到动态平衡时，转速稳定在额定值，整个机电系统保持稳态运行。

5 结论

研究并提出了一种基于单神经元神经网络PID控制算法，并且将该算法应用于无刷直流电机双闭环控制系统的转速环中。分析了无刷直流电机的数学模型和运行特性，介绍了传统PID控制算法的数学原理，设计了基于单神经元神经网络PID的控制算法，最后对比分析了电机控制系统中采用不同算法下的阶跃函数响应，可以得到以下结论。

(1)采用单神经元神经网络PID算法控制下的电机其转速的阶跃函数响应具有更快的上升和调节时间，以及更小的稳态误差。

(2)相比于传统PID控制，单神经元PID算法控制下的电机其转速所达到的稳定值更加贴近于参考设定转速，且转速波动较小。

(3)对比分析三相电流、电磁转矩及反电动势的曲线可知，采用单神经元神经网络PID算法控制下的电机具有更快的响应时间，并且运行更加稳定，鲁棒性更强。