基于Stacking集成模型的网络流量预测研究*

朱国森，郑晓亮

(安徽理工大学 电气与信息工程学院，安徽 淮南 232000)

0 引 言

随着当前网络技术的迅猛发展，为了对网络流量进行有效的控制以及防止网络拥塞，需要对网络流量有较为准确的预测[1]。

当前针对网络流量的预测大部分基于网络流量本身的预测。如时间序列模型的预测研究，包括短相关ARIMA模型[2]、长相关FARIMA模型[3]以及ARMA同其他算法结合的预测方法，如神经网络方法。单一模型已经无法满足现代流量增长的预测，基于各种优化算法的预测模型如PF优化LSTM[4]、改进黑洞算法优化ESN的预测研究[5]等，还有利用算法在不同数据类型上的优势而得到更好结果的组合预测模型、基于小波分解的网络流量预测[6]等。

近年来，随着人工智能在各行各业的发展，相关技术已经被应用于生活的各个方面，如无人驾驶汽车的开发等。基于此，本文基于人工智能机器学习，也即集成学习的角度进行网络流量的预测。集成学习(EnsembleLearning)分为3种，包括Bagging(Bootstrap Aggregating)、Boosting和Stacking。前两者是同一个模型集成的算法，本文采用的是第三种Stacking，它是一种集成不同学习模型的算法，在各个子模型表现较为不错的情况下将其通过一定的方法结合起来。由于不同的模型是从不同角度对数据进行分析的，因此，不同模型集成的算法在一定程度上可以改善预测的表现。

Stacking作为一种新兴的算法，在不同领域均有应用，并且取得了较为不错的结果。文献[7]通过二维向量的Pearson相关系数进行模型的筛选，选取相关性较弱的XGBoost，LSTM，SVM以及KNN算法作为集成学习初级算法进行负荷的预测；文献[8]将Stacking运用于电价的预测，取得了不错的效果；文献[9]根据各个模型的误差参数选取综合表现最好的3个作为基层学习的初级学习器进行患者到达数量的预测；文献[10]通过集成GBDT的方法进行公交车辆到达预测。基于集成学习的预测方法开始在许多方面得以应用，为人们提供了神经网络算法以外的高效学习方法，通过集成不同具有较好预测结果的模型，使得预测结果在原先模型的基础上进一步提高。通过对模型的学习及相关文献的研究，发现不同领域的预测仅是对模型输入因素的不同选择，例如电力负荷预测要求输入高低气温、电价等，网络流量预测则需要高低气温、天气情况等因素。单一预测模型及其改进方法已经在网络流量预测中大量应用，但其准确率无法与多个模型从不同角度对数据的处理结果相比。Stacking方法可以将不同模型的优势结合起来，因此将其用于网络流量的预测。通过Pearson相关系数选取相关性较弱的5个模型作为初级学习器，为了避免可能的过拟合，选择线性回归作为次级学习器，并且根据选取流量的地点加入相关天气因素。通过与各初级学习器以及时间序列的网络流量的比较，证明该方法的可靠性。

1 算法理论及方法

1.1 决策树算法原理

决策树(Decision Tree)在机器学习中是一类较为基础的分类与回归方法，本文取其在回归中的应用。决策树依据使用算法的不同，可以分为3类，分别是基于CART(Classification And Regression Tree)算法、ID3算法以及C4.5算法构建而成。后述两种算法虽然可以挖掘数据的更多信息，但是会使决策树的规模大大增加，因而大部分的决策树使用的都是CART算法。

决策树是一种二叉树型结构，它将特征空间划分成若干单元，每个单元有一个不同的输出，依据数据与该输出的大小关系而选择不同的分支。该输出即对应决策树的节点，当根据停止条件完成空间划分时，所有的节点也就确立了。对于特征空间的划分采用启发式方法，在每一次划分的时候都会对当前集合中所有的特征值，根据平方误差最小的准则，选择最小的一个作为划分点，也即节点中的值。

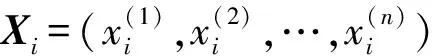
(1)选择最优的(j，s)划分区域。

其中：j为第j个特征变量，s为第j个特征变量的取值，c1和c2为划分后两个区域内固定的输出值。

(2)决定输出值。

划分区域之后，决定相应的输出值：

(3)重复上述步骤，直至满足结束条件。

(4)将输入空间划分为M个区域：R1，R2，…，RM,得到决策树：

1.2 GBDT算法原理

GBDT(Gradient Boosting Decision Tree)是一种提升的决策树算法，它将许多基分类器通过加法模型组合成一个效果更好的学习器。算法的基分类器采用的是CART决策树，分类准则采用均方误差。GBDT算法的步骤如下:

(1)初始化弱学习器。

(1)

当GBDT做回归运算，分类准则为均方误差时，式(1)可表示为

(2)计算样本负梯度。对m=1，2,…,M,计算每个样本的负梯度，也就是残差:

(2)

并且将式(2)得到的结果作为新的输入数据输入到下一棵树中。

(3)计算最佳拟合值。对叶子区域j=1，2,…,J，计算最佳拟合值:

(4)更新强学习器。

(5)得到最终的学习器。

1.3 AdaBoost算法原理

AdaBoost即Adaptive Boosting，是一种自适应增强的学习器。在算法运行的过程中，会对每次迭代的过程进行判断，如果预测的结果和实际值接近，就会降低该值的权重；如果预测的结果和实际值相差较大，则增加该值的权重。再基于上次的预测准确率确定下一次迭代的基权重，重复该过程，最终得到准确率较高的预测结果。

1.4 XGBoost算法原理

XGBoost是GBDT的一种改进方法，相较于GBDT，对损失函数进行了二阶泰勒展开，并且在目标函数之外加入了正则项整体求最优解，进一步减小过拟合的可能。

1.5 SVR算法原理

SVR是一种有监督的学习器。通过寻求结构化风险最小来提升学习机泛化能力，实现经验风险和置信范围的最小化，从而达到在统计量较少的情况，也能获得不错结果的目的。

1.6 Stacking集成算法

Stacking是一种分层模型集成框架。第一层由多个不同的基学习器构成，在本文中选取的是DT，GBDT，AdaBoost，XGBoost以及SVR，在各个模型表现均较为不错的情况下将之集成预测，得到更为不错的结果；第二层选用Linear Regressor，可以进一步避免过拟合。

其具体步骤如下:

(Ⅰ)将数据分为训练数据和预测数据，本文中训练数据为前3 092个数据，后100个为预测数据。再将训练数据进行k折划分，分为数据量相同的k组数据。

(Ⅱ)用每个基学习器进行k次训练，每次训练时用k-1份数据作为训练样本，预测剩下的1份数据，这样可以得到k份训练过后的数据，并且在每次训练的过程中会对100个数据进行预测。

(Ⅲ)将k份预测数据组合起来，得到新的训练样本数据，将得到的k份预测数据取平均值即为新的预测数据。

(Ⅳ)将(Ⅲ)得到的数据输入第二层的Linear Regressor，得到最后的预测结果。

整个过程可用图1表示。

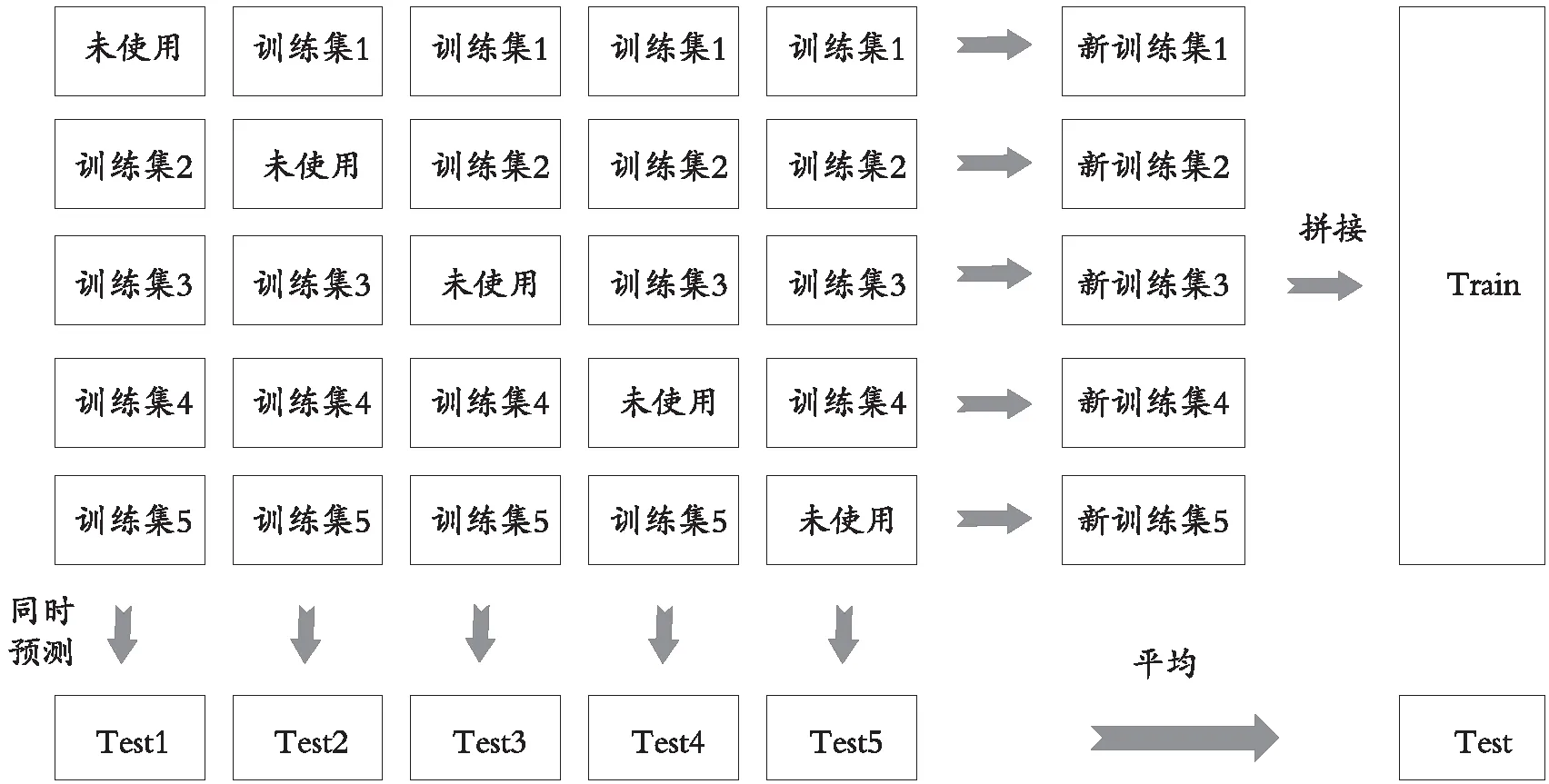
图1 Stacking原理图

在训练过程中，将训练数据分为5份，利用其余4份预测未使用的部分，得到一个测试集，之后通过拼接将得到的5份训练集组合起来成为新的训练集，将5份得到的预测集平均得到新的测试集。对5个选取的模型分别进行上述操作，之后再将Train和Test平均作为新的输入和输出，输入到下一层的Linear Regressor，得到最后的结果。

2 实例分析

实验中的流量数据由淮南移动公司提供，为淮南高铁东站2019-04-14—2019-08-24日 1 h 计的流量数据。以往的流量预测大部分都以流量本身作为预测对象，以前一段时间为输入，预测下一个时间点的流量。在接触季节性差分自回归滑动平均模型以后，结合数据的图形表示，联想到可以将单个一天视为一个周期。考虑淮南高铁东站的距离较远，天气不理想的时候可能会影响旅客的决定，从而影响高铁东站的流量。同不考虑天气情况的预测结果进行对比，验证天气因素确实可以影响流量情况。实验在MATLAB2018a以及Python3.7环境中进行，对于数据的处理使用到了EXCEL以及SPSS软件。具体的步骤如图2所示。

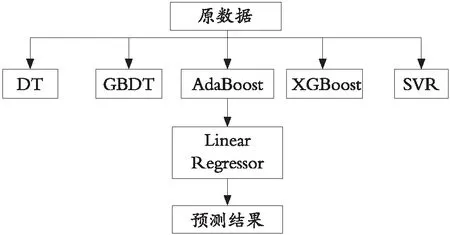
图2 Stacking算法图

为了对模型的实际效果进行验证，使用如下的误差评价指标:

平均绝对误差(RMAE):

均方误差(RMSE):

确定系数(R2):

其中:Y为实际值，T为预测值,n为总的数据个数，SAVE为原始数据的平均值。

2.1 数据处理

数据总量为3 192个，选取前3 092个作为训练数据，预测数据。加入最高气温、最低气温、天气以及小时后，将这4者作为输入，流量作为输出。在进行Stacking操作的时候，为了避免耗时过长，将折数定为5。

在进行数据收集的时候，是以Gb为单位的，凌晨时候的流量较少，显示为0，但还是有以Kb为单位的少部分流量。考虑后期处理数据的时候可能会出现Nan的情况，又因为流量数据只到小数点后两位，在EXCEL中将显示为0的数据替换为0.01。在实验过程中引入了最高气温、最低气温、时间以及天气阴晴情况。最高气温和最低气温分别用实际的摄氏度表示，将天气的阴晴情况量纲化，依照下面所示的表1进行转换。

表1 天气量化对照表

图3所示是调整过后的所有数据展示。

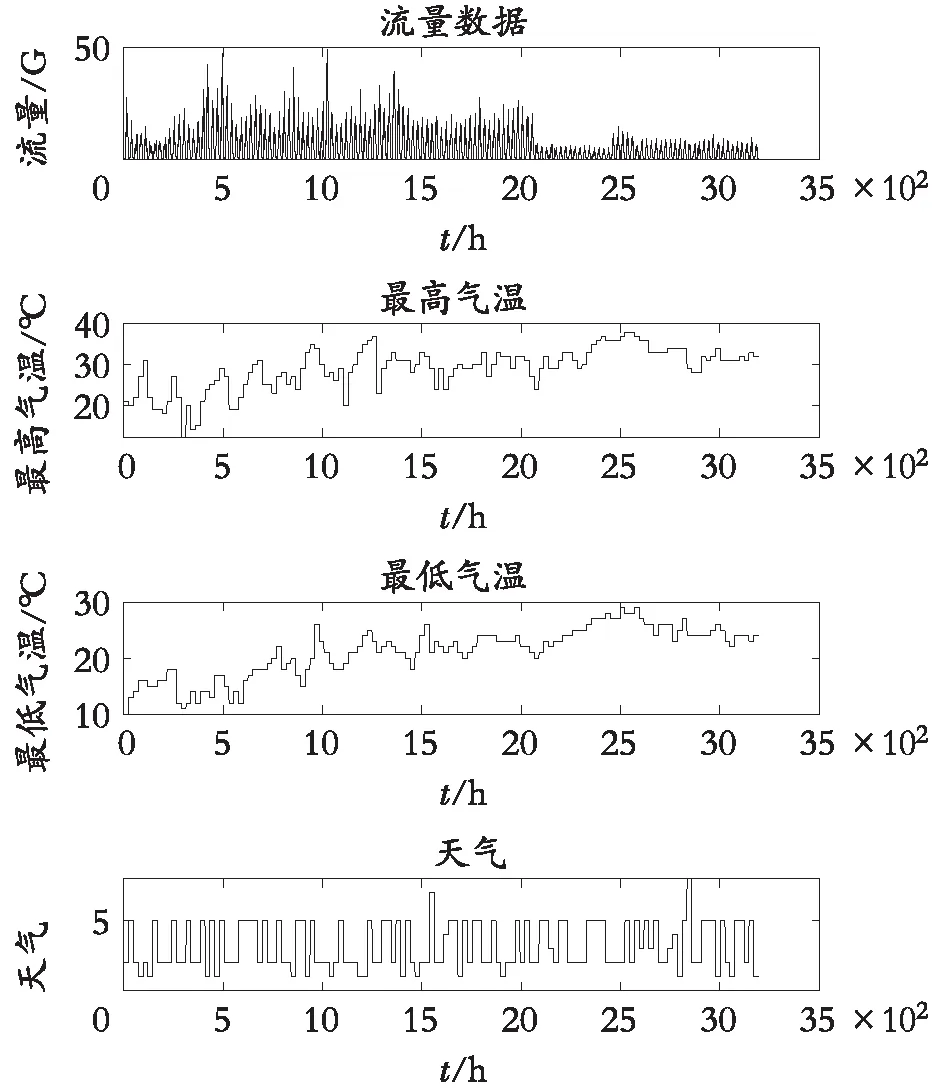
图3 所有数据展示图

从图3的最高气温以及最低气温的波动来看流量数据，当前期相对后期温度较低时，流量相对较高。后期正值暑假，高铁东站距离市区较远，这可能成为人们选择交通工具的一个影响因素。

2.2 模型选择

Stacking作为一种集成算法，可以结合不同的算法。由于不同算法是从不同的解空间对数据进行分析的，Stacking在一定程度上可以很好地结合不同模型的优势。但是并非模型越多越好，当一个模型表现较差的时候，会使得整体算法的预测性能降低。通过对Ridge(岭回归)以及Lasso算法的测试，两者结果成周期性且与实际相距过大，因此排除了这两种算法。对其余7个算法，包括DecisionTree，RandomForest，GBDT，XGBoost，AdaBoost，SVR以及KNN算法分别进行实验之后，显示7者单独预测的结果均不错。从模型少而精的角度考虑，将7个初级学习器预测的结果同实际值作差后，利用二维向量的Pearson相关系数作为相关性指标。在数据处理软件SPSS中进行Pearson相关系数的检验，选择相关性较弱的5个模型作为最后的预测模型。7个模型的相关性表现如表2 所示。

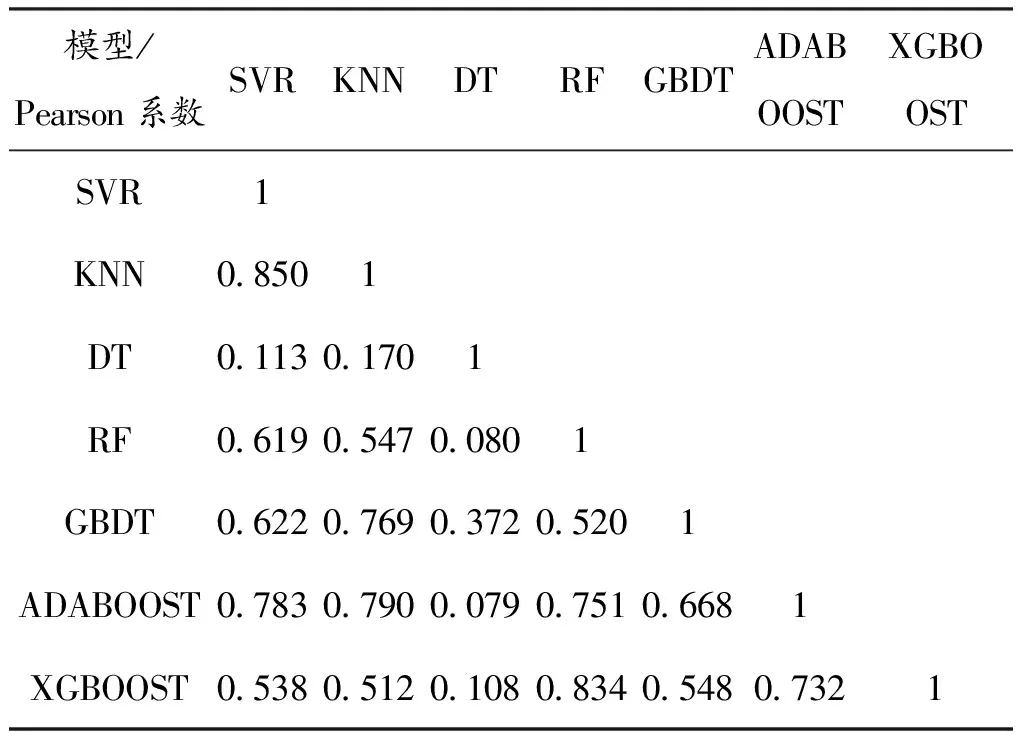
表2 各模型Pearson相关系数对比表

从表2可以看出：SVR同KNN的相关性为0.850，XGBOOST与RF的相关性为0.834，相较于表中其他的相关性较高，因此将KNN模型以及RF模型排除，选择剩下的5个模型作为最后的预测模型。

2.3 Stacking模型预测性能分析

为了验证Stacking模型的性能，选取用于初级学习器的5个模型分别作为对比对象，同时将加入天气因素的Stacking模型同不考虑天气因素的Stacking模型进行对比，验证天气对流量数据的影响。

Stacking模型在Anaconda中使用Python3.7编程实现。取SVR预测结果与Stacking预测结果进行对比分析，如图4所示。

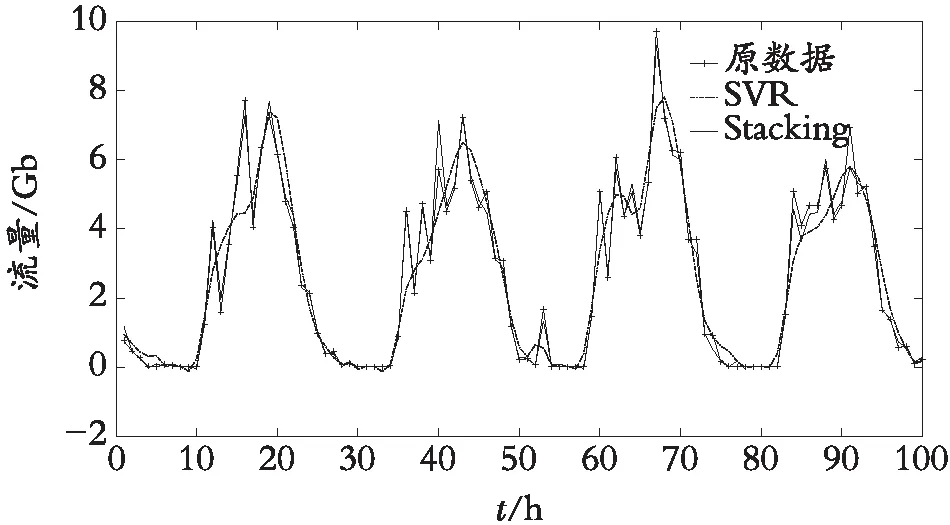
图4 SVR与Stacking模型对比

从图4可以看出：数据存在一定的周期性，符合高铁站的旅客情况。高铁在深夜是禁行的，因此，流量几乎为0。SVR模型对于原始数据的拟合结果也不错，下面通过误差系数来进行各模型的判别，如表3。

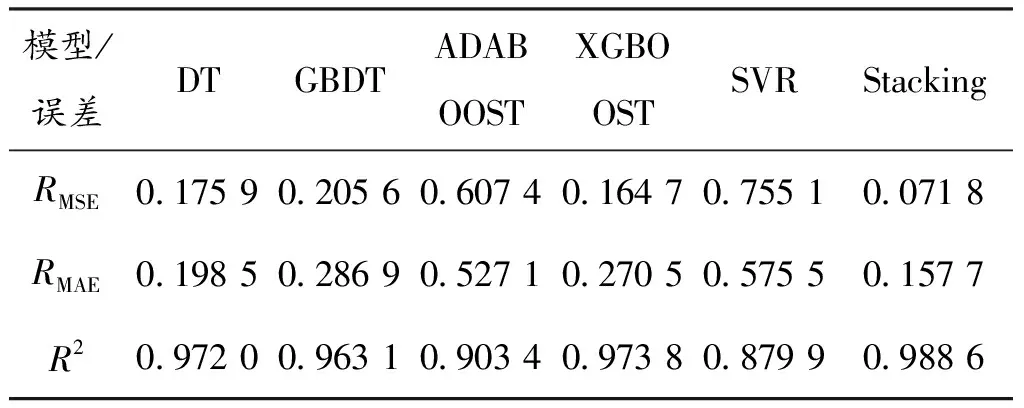
表3 集成模型与基模型误差对比表

从表3可以看出：无论是在RMAE，RMSE还是拟合优度，Stacking模型的结果都是最优秀的，这可以归因于它利用不同模型相互补足。

再将加入天气因素的Stacking模型同不考虑天气因素的Stacking模型进行对比，如图5所示。

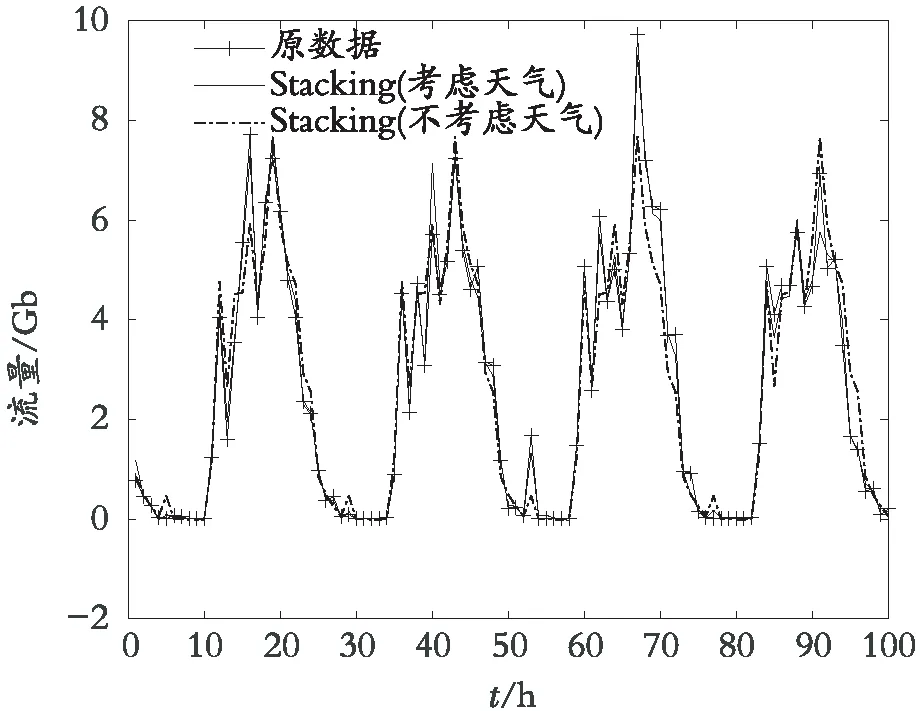
图5 有无天气因素对比图

从图5可以看出:不考虑天气因素的预测结果在一些小的突起方面的表现不如考虑天气Stacking的预测结果，整体的拟合也不如考虑天气因素的Stacking，从表4中的误差参数中也可以很明显地看出来。

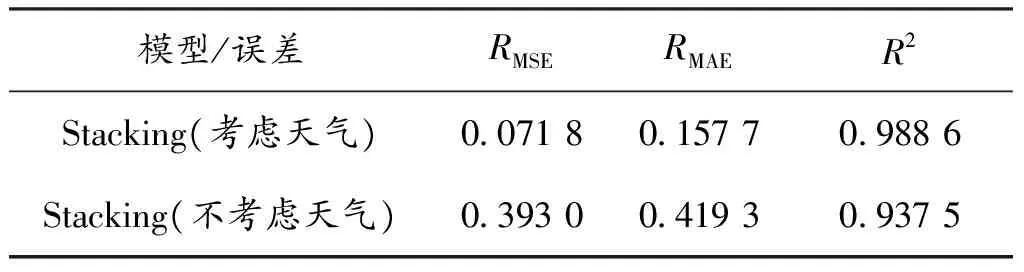
表4 Stacking与时间序列误差对比

3 结 论

结合高铁站的地理位置，将天气因素量化后加入预测。仿真证明：加入天气因素之后的预测结果相较于未加天气因素的预测结果更接近实际情况。Stacking集成算法作为当下流行的算法，很好地结合了不同算法，并且各取所长，得到了较各基模型更为优秀的结果。通过Pearson相关系数的检验，筛选出相关性较弱且表现较为不错的几个模型。通过结合不同的模型，可以从不同的角度对数据进行处理，进而得到更为准确的结果。

参考文献(References):

[1] 党小超,阎林.基于多元线性自回归模型的流量预测[J].计算机工程,2012,38(1):84—86,89

DANG X C，YAN L.Flow Prediction Based on Multiple Linear Autoregressive Model[J].Computer Engineering，2012,38(1):84—86,89(in Chinese)

[2] 党小超,阎林.基于短相关ARIMA模型的网络流量预测[J].计算机工程,2012,38(13):71—74

DANG X C，YAN L.Network Traffic Prediction Based on Short Correlation ARIMA Model[J].Computer Engineering，2012,38(13):71—74(in Chinese)

[3] 李士宁,闫焱,覃征.基于FARIMA模型的网络流量预测[J].计算机工程与应用,2006(29):148—150

LI S N，YAN Y，QIN Z.Network Traffic Prediction Based on FARIMA Model[J].Computer Engineering and Application，2006(29):148—150(in Chinese)

[4] 李校林,吴腾.基于PF-LSTM网络的高效网络流量预测方法[J].计算机应用研究,2019,36(12):3833—3836

LIX L，WU T.Efficient Network Traffic Prediction Method Based on PF-LSTM Network[J].Computer Application Research，209,36(12):3833—3836(in Chinese)

[5] 韩莹,井元伟,金建宇,等.基于改进黑洞算法优化ESN的网络流量短期预测[J].东北大学学报(自然科学版),2018,39(3):311—315

HAN Y,JING Y W，JIN J Y,et al.Short-term Network Traffic Prediction Based on ESN Optimization Based on Improved Black Hole Algorithm[J].Journal of Northeast University(Natural Science Edition)，2008,39(3):311—315(in Chinese)

[6] 崔兆顺.基于小波变换的网络流量组合预测模型[J].计算机工程与应用,2014,50(10):92—95,100

CUI Z S.Network Traffic Combination Prediction Model Based on Wavelet Transform[J].Computer Engineering and Application，2014,50(10):92—95,100(in Chinese)

[7] 史佳琪,张建华.基于多模型融合Stacking集成学习方式的负荷预测方法[J].中国电机工程学报,2019,39(14):4032—4042

SHI J Q，ZHANG J H.Load Prediction Method Based on Multi-model Stacking Integrated Learning[J].Chinese Journal of Electrical Engineering，209,39(14):4032—4042(in Chinese)

[8] 王曙,潘庭龙.Stacking集成模型在短期电价预测中的应用[J].中国科技论文,2018,13(20):2373—2377

WANG S，PAN T L.Application of Stacking Integration Model in Short-term Electricity Price Prediction[J].China Science and Technology Paper，2008,13(20):2373—2377(in Chinese)

[9] 李瑶琦,周鑫,高卫益,等.基于Stacking集成学习的急诊患者到达预测[J/OL].工业工程与管理:1—10[2019-12-29].http://kns.cnki.net/kcms/detail/31.1738.T.20190606.1341.004.html

LI Y Q，ZHOU X，GAO W Y，et al.Arrival Prediction of Emergency Patients Based on Stacking Integrated Learning[J/OL].Industrial Engineering and Management:1—10[2019-12-29].http://kns.cnki.net/kcms/detail/31.1738.T.20190606.1341.004.html(in Chinese)

[10] 荆灵玲,解超,王安琪.基于集成学习的公交车辆到站时间预测模型研究[J].重庆理工大学学报(自然科学版),2019,33(10):47—53

JING L L，XIE C，WANG A Q.Prediction Model of Bus Arrival Time Based on Integrated Learning[J].Journal of Chongqing University of Technology(Natural Science Edition)，2019,33(10):47—53(in Chinese)