横向连续性保持的自适应经验小波变换算法研究

杨 超

（成都理工大学，四川 成都 610000）

0 引 言

时频分析一直是非平稳信号分析与处理的有效手段。D.Gabor于1946年提出了一种同时用时间和频率表示信号的方法，即Gabor展开，代表着时频分析方法的产生。COHEN L在分析语音信号时，提出了短时傅里叶变换[1]。短时傅里叶变换利用加窗的方式实现了对信号的时频局部化分析，而小波变换则采用可变的窗口实现了对信号特征的多尺度刻画，这些方法虽然在一定程度上实现了信号局部特性的分析，但仍具有一定的局限性[2,3]。

经验小波变换（Empirical Wavelet Transform，EWT）是在小波变换的基础上提出来的，该方法通过对信号的傅里叶谱进行自适应划分，然后建立相应的小波滤波器组进行滤波来提取不同的IMF分量，具有完全的自适应性[4-7]。由于经验小波变换计算方便，不存在模态混叠问题，因此该方法被广泛应用于各个领域。

传统的经验小波变换是基于极大-极小值的方法来检测傅里叶谱的边界，在实际工作中受噪声干扰容易产生过分割或欠分割等问题[8-10]。基于此，本文提出了一种基于经验小波变换和数学形态学相结合的方法。首先通过形态学滤波来获得信号的包络，其次在此基础上进行频谱划分，降低了频谱划分错误率，并提高了信号的分解效果。

1 数学形态学理论基础

经验小波变换具有良好的自适应性，但是实际信号复杂的频谱会导致分割边界难以确定，而数学形态学能够很好地保留信号频谱中的形状信息，并将不重要的部分去掉，具有良好的去噪效果，因此将两种方法结合用于信号分析。

数学形态学基本运算主要包括腐蚀、膨胀、开运算与闭运算。腐蚀与膨胀基本定义为：

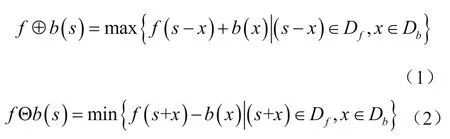
式中，f表示原始信号；b表示结构元素；Df与Db分别是f与b的定义域。

开运算是利用相同的结构元素对信号先膨胀再腐蚀，闭运算则是先腐蚀再膨胀。两者的定义分别为：

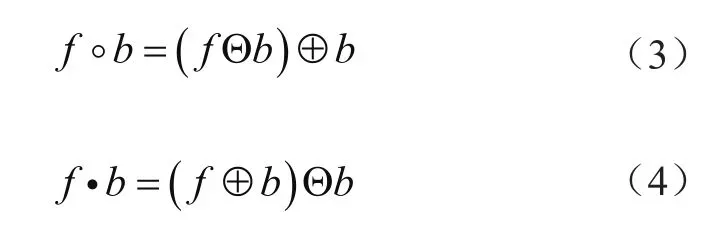
2 改进的经验小波变换

经验小波变换的实质是建立了一组带通滤波器，通过提取信号中不同频率段的分量来分离不同的模式。经验小波变换的原理如下文所述。

步骤一：对于实信号f(t)，将信号的频谱分为N个连续区间对经验尺度函数和经验小波函数分别定义为：

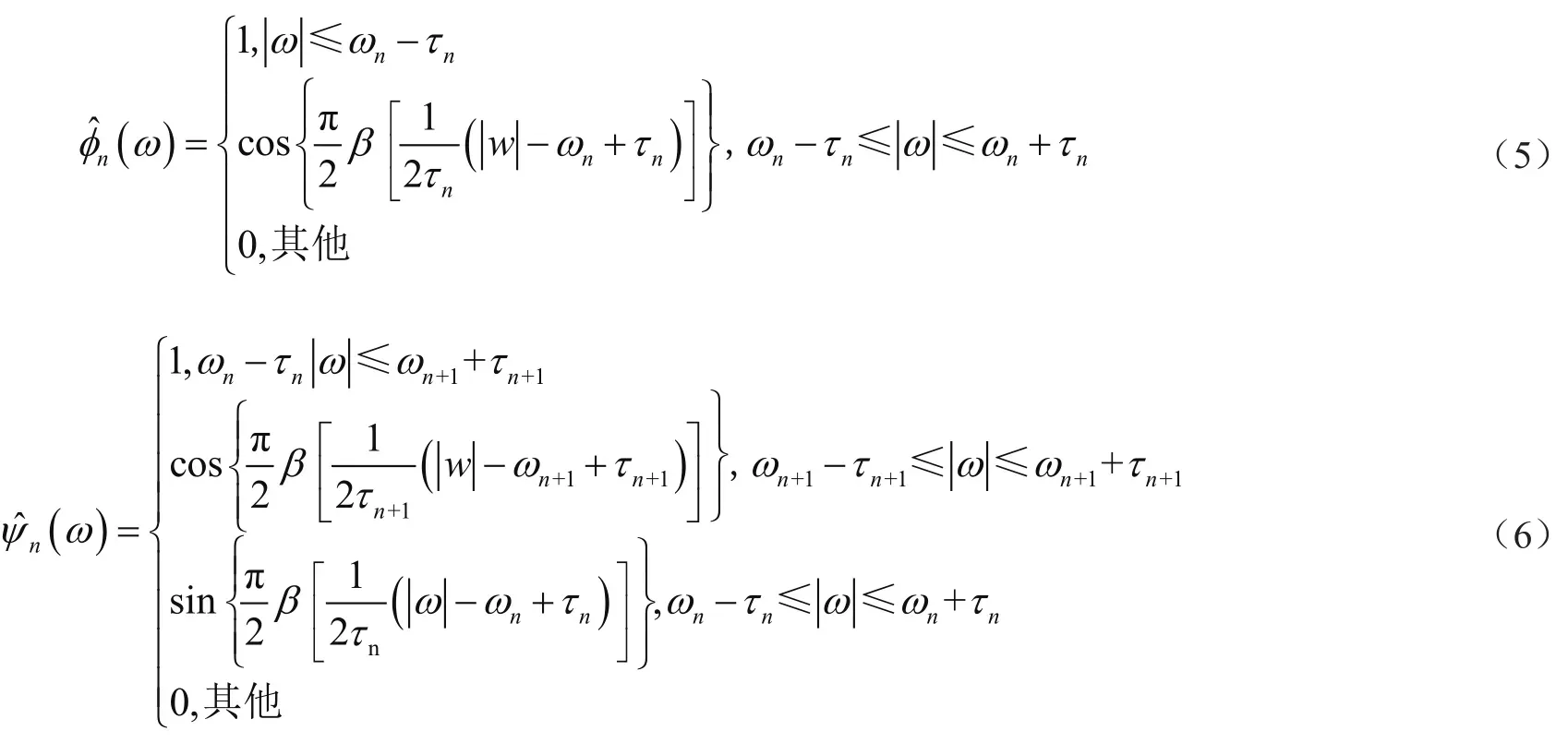
其中，函数β(x)是在x∈[0,1]上满足如下条件的任意连续函数：

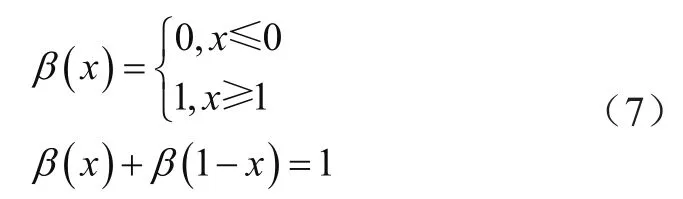
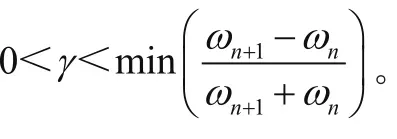
步骤三：通过信号和经验小波函数与经验尺度函数的内积获得细节系数与近似系数。计算公式为：

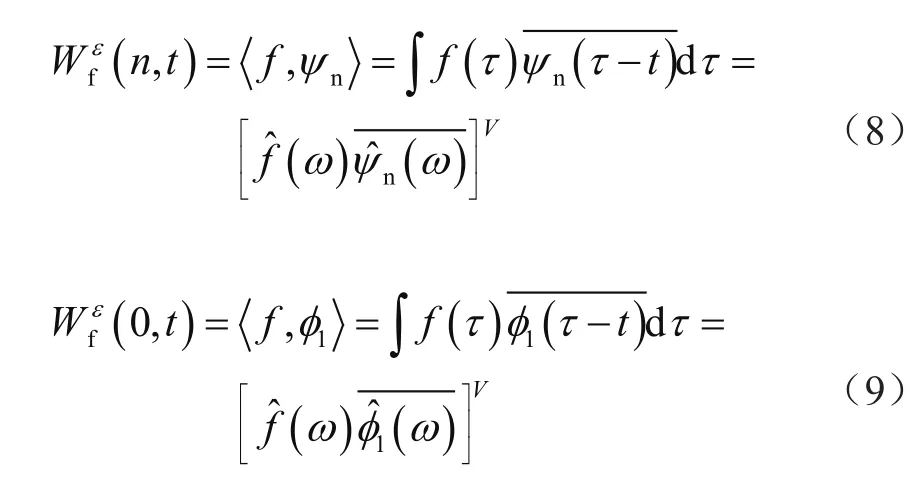
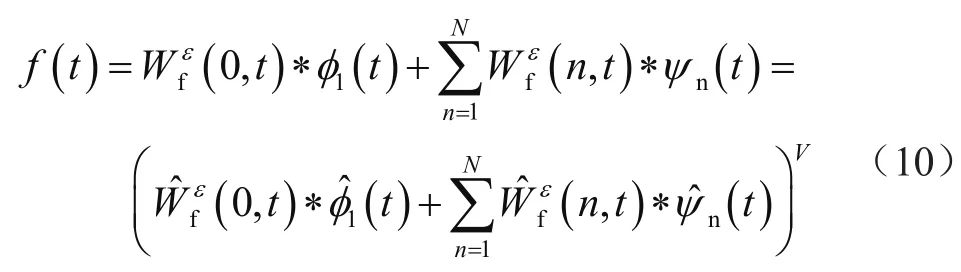
分解公式为：

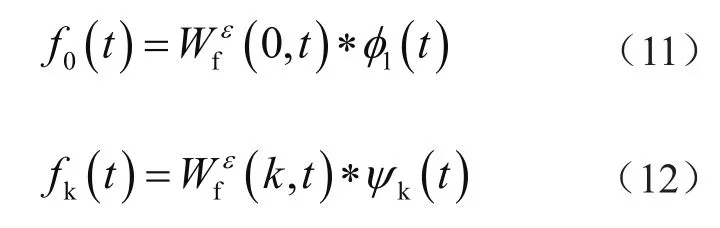
3 实际数据测试

利用已有的地震资料来对改进方法的效果进行分析。为了简便，选取其中一道地震信号，其时域图如图1所示。

图1 地震信号时域图

首先，通过傅里叶变换得到信号的频谱。图2（a）展示了信号的频谱及经验小波变换边界检测结果。从中可以看出，由于噪声干扰，在主频处的极值点较多，并且相邻的极大值或极小值间隔较小，而经验小波变换是基于频谱极大值来检测分割边界，因此产生了许多不必要的分割，分离了从属于同一模式的成分。图2（b）中，经过形态学滤波后，地震信号的频谱包络被正确的勾勒出来，随机噪声被滤除形态滤波。与经验小波变换相比，改进方法不仅检测出了不同的模式，而且边界之间有明显的间隔，其效果有了明显提升。

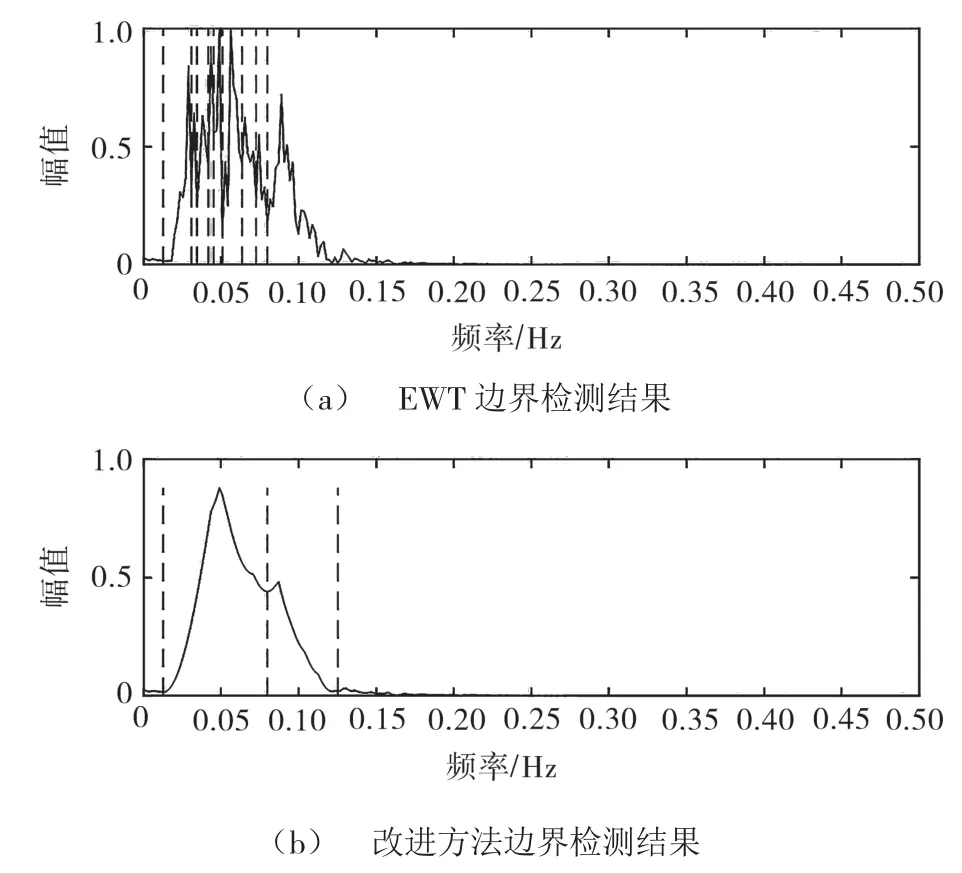
图2 检测结果

其次，为验证同时处理多道地震的效果，每隔60道信号选取一道地震信号。从不同地震信号的频谱图（图3）与边界检测结果（图4）可以看出，各道地震信号的包络都表现出先升后降的趋势，但主频的宽度有所不同。此外，噪声干扰也使信号在主频处表现出不同的振荡行为，如第4道信号在主频处包含了明显的低谷部分。尽管如此，改进方法仍然检测出了不同的IMFs分量，且不同的信号具有一致的边界分割点，证明了改进方法的有效性。

图3 不同地震信号的频谱图

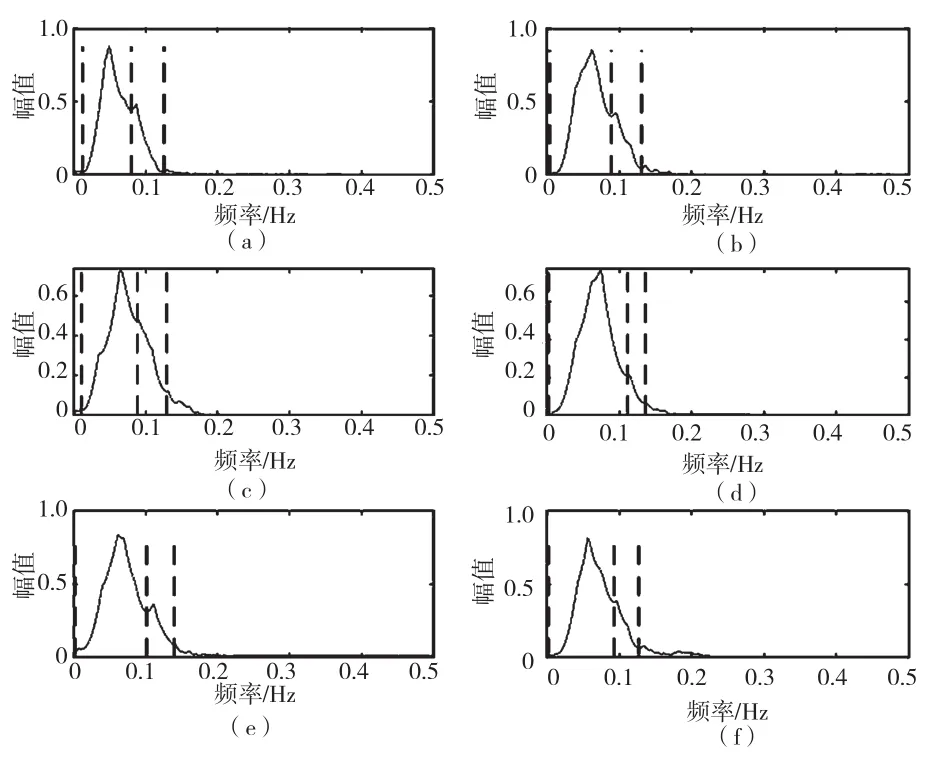
图4 不同地震信号边界检测结果

最后，将改进的EWT算法用于分析其他道的地震信号。获取原始剖面图（图5）后，提取不同IMFs分量剖面（图6）。与原始剖面相比，大部分地震信号信息都包含在图6的剖面（b）中，不同的剖面也有较大差异，说明改进方法成功分离了地震信号中的不同分量。

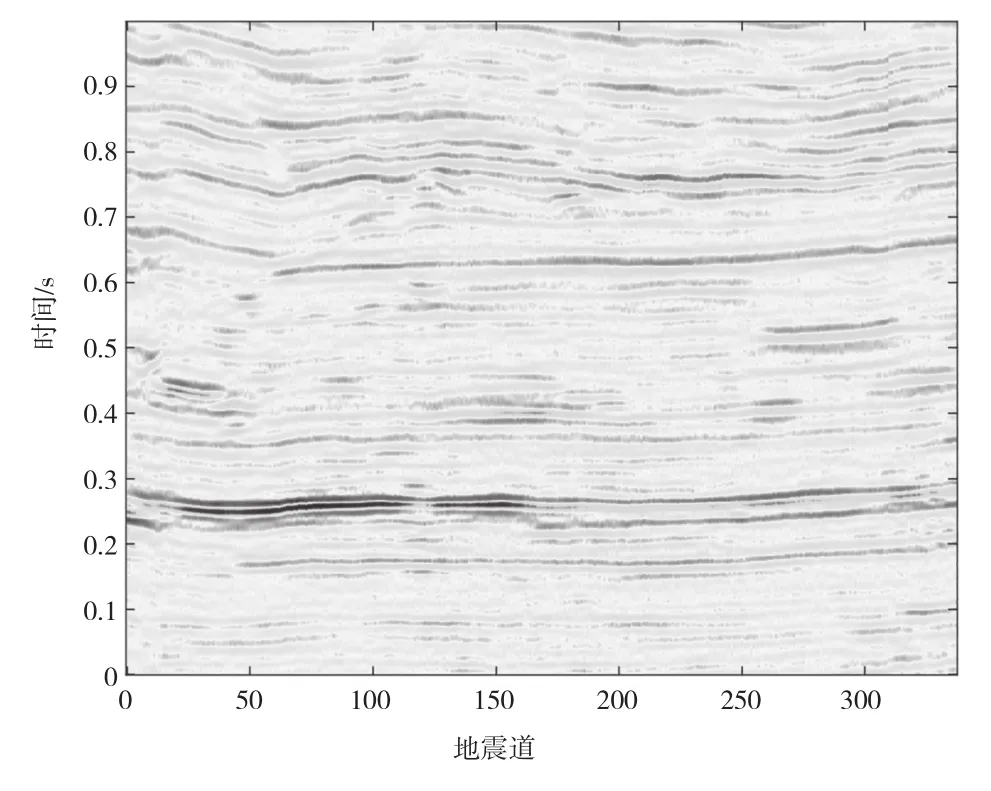
图5 原始地震信号的剖面图

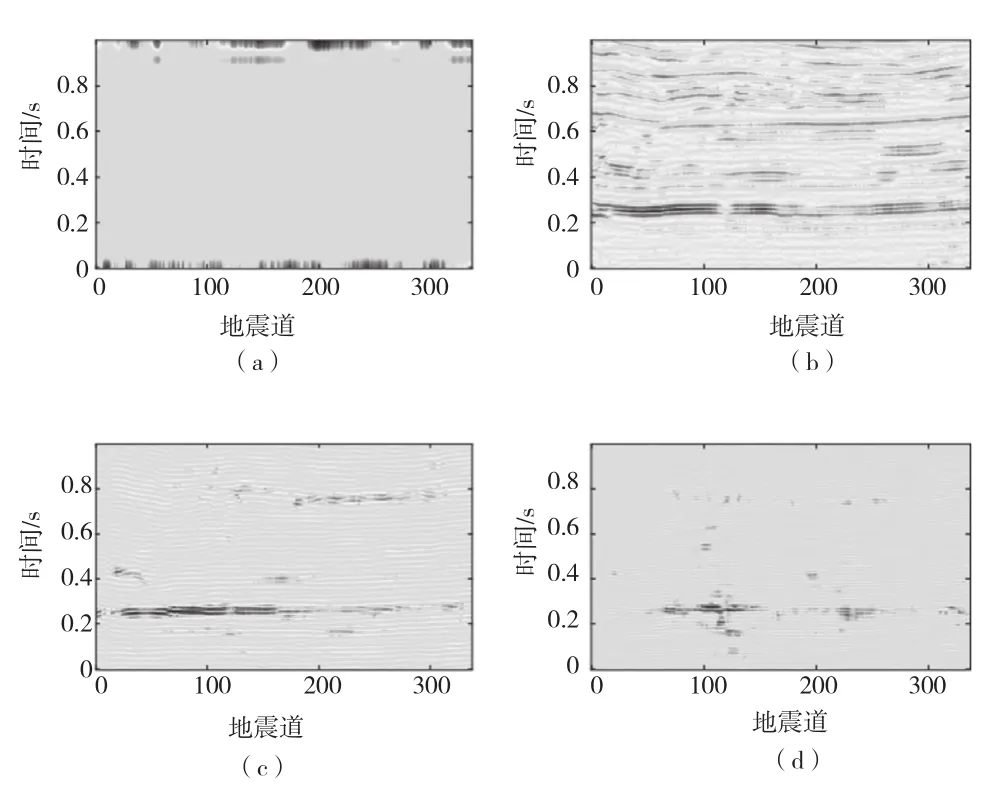
图6 不同IMFs分量的剖面图

4 结 论

将经验小波变换与数学形态学相结合，先通过形态学滤波来获得信号频谱包络，然后在此基础上进行边界检测，解决了经验小波变换方法在处理复杂频谱时存在的过分割问题，有效降低了频谱划分错误率。在多道地震信号的处理中，该方法得到了一致的边界分割结果，对横向连续性进行了证实。此外，将此方法运用于所有地震信号，最终得到了分离良好的IMFs分量剖面，进一步证明了其实际应用效果。