基于节点法的EIT重构技术研究
郑皓楠
(西北工业大学,陕西 西安 710100)
0 引言
电阻阻抗成像(EIT)是基于生物体组织在不同的生理、病理状况下的电阻抗(电导率、电阻率)分布差别较大的特点,并通过电极在生物体表面施加微小的激励电流,从而使生物体的组织内部产生微弱的电场,利用在体表测得的电压信号配合一定的成像算法以实现组织内部电阻抗分布图像的重构。电阻抗成像具有用途广泛、健康环保安全、经济可循环使用以及快速便捷易用等优点。
1 EIT技术简介
EIT系统的基本原理是通过多路开关向安装在被测生物体组织表面的电极注入安全激励信号,同时通过测量目标区域表面能够反映阻抗信息的电压信号,该信号经过高精度的放大电路处理后,通过相敏解调电路和A/D转换器进行信号恢复和数字化处理,最后计算机通过图像重构算法得到能够反映被测区域生物体组织电阻抗变化的图像。电阻抗数据检测系统的功能是采集生物体组织的电阻抗及其变化信息,图像重建根据电阻抗数据检测系统提供的生物体组织的电阻抗及其变化信息,采用相应的重建算法对生物体组织的电阻抗及其变化信息实现图像重建与显示的功能[1],如图1所示。

图1 EIT成像系统
EIT成像的难点是在对其场域数学模型的合理构建上,由于生物体内的电磁场为非线性分布,因此,在实际测量中会受到接触电阻抗的影响,而建模过程又会忽略这些因素(例如生物组织电阻抗信息虚部和生物体接触电极后产生的电阻等),在模型构建中将高阶项以有限元离散化的形式产生计算误差,该计算误差在迭代过程中不断累积,导致EIT图像重构后的分辨率较差;且用模型求解逆问题存在病态性,其病态性表现在边界电压出现微小变化就会造成解的巨大变化,且现有算法对区域中心的变化不敏感,对区域边界的变化敏感[2]。此外,电阻抗成像技术计算量较大,成像速度较慢,想要提升重构图像的分辨率就必须对物体场域进行密集剖分,该操作会导致有限元剖分呈几何级增长。如何在提升图像质量的同时保证不会出现计算量大幅度增加的情况,这就需要在重构算法上进行改进优化。
2 EIT正问题、逆问题求解
EIT图像重建过程是指通过边界测量数据进行图像重建,对被测生物内部阻抗的分布处理主要分为正问题和逆问题2个求解过程[3]。电阻抗成像的正问题是在已知电导率分布和边界条件的情况下求取场域内的电位分布。求解EIT正问题主要以解析法和数值计算法为主,但解析法受区域内的条件所限制,当电导率不均匀或二维形状不规则时,其解析推导难度较大,因此首选数值法;常用的数值法包括有限元法、有限差分法以及边界元法[4]。该文正问题计算采用的是有限元法。电阻抗成像的逆问题是在已知边界电压的情况下,求得目标区内电导率(电阻抗)的分布,如图2所示。
EIT图像重建的本质就是求解逆问题,求解逆问题的实质就是形成阻抗图像;但是,由于逆问题的不适定性,因此,它的求解过程存在一定的难度。EIT逆问题的求解过程是1种严重病态非线性问题的求解过程,其主要表现在以下4个方面:1) 因为微小的边界电压波动就会造成解的不确定性,影响成像质量,所以对成像算法提出了很高的要求。2) 测量得到的边界电压数量有限,激励信号形式单一,不足以完全反应出人体内部阻抗的变化情况。3) 场域内电导率的分布与测量边界电压的非线性关系,是由电磁场的软场特性决定的。4) 电阻抗的求解是通过算法不断迭代来获得近似解,因此,它的值和实际值存在一定偏差。

图2 求解EIT逆问题的示意图
为了简化问题,假定被研究区域的电流场是准静态场,以二维EIT问题为例,EIT的图像重建问题实质上是求解1个低频电流场的逆问题,即已知边界的电流和电压,求解内部电导率的分布。该文逆问题求解以静态成像求解为研究对象,鉴于逆问题求解上述4种表现,因此在选择图像重建算法的过程中需要非常谨慎。EIT逆问题求解通常采用修正的牛顿-拉夫逊迭代算法(MNR算法)[5]。
EIT逆问题求解主要基于最小二乘理论,如公式(1)所示。

由于EIT逆问题具有严重的病态非线性问题,因此公式(1)常用MNR算法求解。假定将场域离散成m个单元(选用FEM三角形网格剖分方式),边界测量电极为L个。选择相临电极施加激励电流且采用相临测量的方式,就可以获取L×(L-3)个边界电位数。据此可以推导出MNR算法的迭代式,如公式(2)所示。

式中:k为迭代次数。
为了解决逆问题求解的病态非线性问题,常在求解过程中进行正则化处理,EIT逆问题中最常用的正则化算法就是Tikhonov正则化算法。该算法的实质是通过构造特定形式的罚函数来实现对解的阻尼作用,以求得稳定的解。
引入正则化后,其迭代式如公式(3)所示。

式中:k为迭代次数;λ为正则化参数;T为转置符号;R为由FEM模型逆时针进行单元编号得到的正定矩阵;v'是电压值关于电导率的导数。
对矩阵元素Rij,i=j时,Rij为单元数之和;i≠j时,i与j单元格相邻,Rij=-1;i与j单元格不相邻,Rij=0。R及正则化参数的非负性使其逆项矩阵的求解过程更加稳定。
3 基于MNR算法的中心局部细剖分模型
电阻抗成像图像重建效果的好坏受激励模式、数据采集精度、算法以及剖分规模等多方面因素的影响,其中剖分规模是最重要的影响因素之一。为了平衡正问题和逆问题求解过程中因疏密不同而带来的不必要的影响,同时尽可能地避免出现计算量过大的细剖分方式,通常会采用密剖分三角形网格模型和疏剖分三角形网格模型结合的均匀剖分方式。电阻抗成像图像重建算法中逆问题计算是建立在正问题计算之上,正问题计算精度越高,图像重构的质量也越好;因此,正问题通常采用密剖分求解(在疏剖分单元三边中点两两连接得到密剖分模型),逆问题选择疏剖分求解。但疏密结合的均匀剖分不能从根本上解决对计算正问题和逆问题带来的影响。因此,假定连续求解的仿真物理模型为规则的圆域(圆域半径为16),运用有限元剖分软件[6]选择有限元法(FEM)进行三角形剖分,对以中心区域为圆心,半径为1/2的圆形区域进行中心区域局部细剖分(如图3所示),应用牛顿-拉夫逊算法进行图像重构,并将中心区域的目标与粗细剖分界面的目标进行对比,如图4所示。

图3 中心区域局部细剖分模型
图4(a)和图4(b)分别是异物位于中心区域的疏、密剖分和中心区域密剖分的仿真成像,图4(c)和图4(d)分别是异物位于非中心区域的疏、密剖分和中心区域密剖分分界面处的仿真成像。对比图4(a)和图4(b)可知,图4(b)成像均匀,伪影小,定位准;对比图4(c)和图4(d)可知,疏、密剖分和中心密剖分仿真成像相差不大。通过以上仿真成像对比发现,如果异物处在分界面上,那么中心局部密剖分相对疏、密剖分仿真得到成像结果改善不大;如果异物整体处于密剖分部分内,那么中心局部密剖分相对疏、密剖分就可以得到更加良好的仿真效果。因此,对于异物采用中心局部细剖分有助于提高重构成像的质量。综上所述,细剖分不一定要处于中心位置,它可以根据异物的位置灵活地确定细剖分剖分的位置。
4 基于节点法的EIT图像重构技术及仿真实验
4.1 重构算法
采用基于牛顿-拉夫逊算法的局部细剖分能够在无噪仿真实验中构建高质量的EIT阻抗变化分布图,但电阻抗成像图像重建效果的好坏受多方面因素的影响,其中包括测量噪声。为了使仿真实验成像切合实际,需要对其进行加噪处理。仿真实验表明,经过加噪处理后的数据重建的异物区域图像会产生向粗细剖交界面偏移的现象,这会导致EIT重构图像存在偏差,形成该现象的原因多为FEM网格单元剖分不均匀;而将单元退化成节点后进行成像,由于节点的位置同等,因此会最大程度地避免出现剖分不均匀的问题,从而有效地解决了异物区域发生偏移,产生定位偏差的现象。其过程如下:1) 设定迭代条件,为无穷小,U为实测边界电压值,Uk为均匀阻抗时正问题求解的边界电压值,满足时,可以终止迭代并进行图像重构,不满足该条件则进行下一步。2) 基于单元阻抗信息计算单元雅克比矩阵J(σk)。3) 根据第2步的结果计算节点雅克比矩阵及节点阻抗迭代步长h,h的计算公式如公式(4)所示。

图4 单目标仿真图像
4.2 仿真成像
以单目标为仿真对象,向仿真数据中加入10 db、40 db的高斯白噪声,通过节点法形成EIT图像重构,如图5所示。
图5(a)和图5(b)为10 db信噪比条件下局部细剖分及基于节点法的局部细剖分成像结果,图5(c)和图5(d)为40 db信噪比条件下局部细剖分及基于节点法的局部细剖分成像结果,对比可知在信噪比同为40 db(较高)的条件下,2种成像质量虽有差别(图5(d)优于图5(c)),但其差异较小;在信噪比同为10 db的条件下,2种成像质量差别很大,图5(b)的效果比图5(a)的效果要好。由此可见,信噪比越小,节点法的成像效果越好。综上所述,使用节点法成像能够去除因局部细剖分而产生的影响图像重构质量的不利因素,因此,对异物采用局部细剖进行图像重建是可行的。
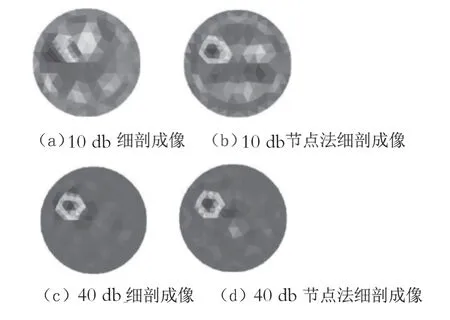
图5 不同噪声条件下单目标仿真成像
5 EIT应用讨论
电阻抗成像技术是近几十年发展起来的新一代无损功能成像技术,其与现有成像技术相比具有很多优点,但是仍然存在很多需要研究解决的问题。该文利用现有技术所提供的结构先验信息构建了可以有效提升模型准确性的EIT仿真模型,通过MATLAB平台[7]进行仿真计算,在牛顿-拉夫逊算法的基础上改进网格剖分,构建基于异物区域的局部细剖分模型,在仿真过程中展现了一定的优越性,但是在抗噪性能上还存在一定的改进空间;因此,将单元细化成节点,通过节点进行成像,可以减少边界伪影,提高成像质量,得到高分辨率的图像。
6 结语
电阻抗图像重建在临床研究中仍然具有一定的挑战性,如果在临床研究中与其他医学图像结合研究将会进一步推动它的应用和发展,还可以最大程度地发挥其无损功能性成像的优势。改进后的EIT图像重构算法抗噪性能还有待提高,且未对生物体组织进行试验,因此后续还应该进一步提高算法成像的精度,加深对于逆问题的求解。总之,构建具有较高检测灵敏度和性噪比、有足够的空间分辨率和阻抗分辨率[8]以及优化现有算法重建高质量图像效果的成像系统是当前科研工作者努力的方向。

