以形促思 演绎算理
——以小学数学乘法的计算为例
唐 林
(贵州省遵义市播州区乐山镇新土小学 贵州 遵义 563000)
1.数形结合,整合乘法口诀
乘法计算教学中最基础为乘法口诀的教授,教师需制作乘法计算表,通过其中数据的整合与补充,引导学生以形促思,从面到点,在从点到线,发现与掌握乘法规律,完整学习乘法口诀。教师利用数形结合教学方法,完成乘法口诀计算变式,以此补充传统“小九九表”的不足,并培养学生数学思维。《乘法现实情境模型的有关研究》中,对整数乘法模型的构建有几种方法。如配对模型;矩形模型;倍数模型等。其中矩形模型的直观性与形象性更强,可帮助学生在等量组的集合上,提供直观表象,并在图形的观察过程中掌握分数乘法的算理。另外根据有关调查可知小学生对矩形模型的理解还比较轻松,不会因为其中数据的变化而提升学习难度。所以可以将此做为数形结合教学的基础模型。教材中对于乘法计算方面的内容,还没有矩形模型方面的内容,所以教师可从乘法计算表中探索图形信息,然后为学生展示图形,以动静结合的形式让学生观察乘法口诀中的奥秘,深入学习乘法口诀[1]。通过数形结合教学,不但丰富学生对乘法口诀的理解,还能在矩形图中找出数与数相乘的算理,掌握基础的函数思想。
2.找准方向,演绎算理
在三位数乘一位数学习基础上,本文以三位数乘以两位数计算为例,借助数形结合方法,引导学生推导计算方法,归纳计算的算理与算法,在学习中养成紧密思考的良好习惯,进而自主思考。教学过程为:
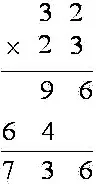
2.2 新课传输。当学生对两位数乘以两位数竖式笔算熟练掌握之后,三位数乘以两位数的教学就可在教师的引导下,由学生自主计算。如120×23,经过之前点子图的导入,学生解此问题的时候,同样想到使用点子图,但是发现数字太大,图形中函数太多,反倒给计算带来困扰。教师提示可以将电子图变成长方形,这样120×23就成了计算长方形面积的过程。教师先为学生展示图形,并提问“请你说一说你的计算过程”。结合上面复习的过程,学生大多数想到的是先计算120乘以3的积,得到360个一。然后计算120乘以2,得到有240个十,将两部分结果相加,就是120×23得数。此环节的设计将学生列为学习主体,自主探究三位数与两位数相乘计算方法,并从点子图过渡到长方形面积,升华图形,并让学生在直观观察下,加深对算理的理解,同时为将来学习乘法分配律奠定基础。
学生完成计算后,教师对其进行鼓励,并在师生对话中,完成新旧知识的连接,将新知识纳入到学生自身知识脉络中,完成内化。如教师提问“我没有在课堂中教过三位数乘以两位数的算法,但是你们也都自己算了出来准确答案,你们真棒。我想知道你们是怎么计算出来的”学生回答“三位数乘以两位数与两位数乘以两位数的方法相同,都是先求出后面乘数中个位与前面乘数相乘,得到几个一,然后后面乘数的十位与前面乘数相乘,得到几个十,然后相加。”通过数形结合,让学生更加容易理解,并建立正确思考方向。
2.3 扩展练习延伸乘法计算知识。三位数乘以两位数计算本质被学生充分掌握后,教师就可出示与其有关的应用题,如山东威海旅游社推出青岛到威海两日套餐,每人311元,本团报名有32人,请问旅游社一共收到多少钱?学生先根据题目列式,311×32。接着不让学生直接计算,而是教师提问“有一名同学算出旅行社需收9356元钱,请你估算一下,这个结果对吗?”让学生先将两个数的个位数相乘,即1×2=2,就可知道311×22得数的个位数为2,与得数9356不相符,就可直接回答这名同学计算错误。教师接着提问“旅行社的收银员想用计算器计算,但是经过实践发现计算器中数字2的键是坏的,你能否用这个坏了的计算器计算311×32”[2]。此问题难度较大,可引导学生借助图示,将原式分解为311×31+311。然后再使用计算器计算,让学生在此过程中扩展学习思维,在图形的引导,快速理解,展示算理。
结论
综上所述,在乘法计算教学中,如果将其转化为图形的形式,会让学生更快速掌握计算算理,并能创新出新的解题方法。实现以形促思,演绎算理。

