基于GSL&PS-PGSA的刚构桥主梁截面设计优化研究

唐建东

摘要：文章以河池至百色高速公路某施工段红水河特大桥为工程背景，基于生长空间限定与并行搜索的算法组合新机制（GSL&PS-PGSA）算法，结合Midas软件建立的仿真计算分析模型，以主梁结构总重为目标优化函数，各节段截面编号为设计变量，结构施工过程中的刚度、强度及稳定性为约束条件，对刚构桥主梁截面进行了結构设计优化。优化结果表明：优化后施工过程中主梁最大拉应力减少了16%，最大压应力减少了13%，最大变形减少了26%，主梁结构自重优化后减小了8.5%。

关键词：桥梁工程;刚构桥;GSL&PS-PGSA;截面设计优化

0 引言

刚构桥作为高速公路最常见的桥梁类型之一，其整体性好，适用性广，颇受各国设计者的喜爱，国内对刚构桥的研究已不胜枚举，胡斌[1]等基于灰色预测方法，建立了大跨径刚构桥GM（1，1）预测主梁施工线形抛高值的模型，通过对比模型预测与实测数据分析了预测精度及其影响因素[1];闫维明等通过缩尺模型试验，研究了高墩连续刚构桥在近断层脉冲型地震动下的抗震性能[2];张炳鑫等考虑梁端碰撞作用，基于OpenSees平台建立了某大跨高墩连续刚构桥非线性有限元模型，计算了桥梁主要构件的地震易损性曲线，研究了桥梁梁端碰撞效应对桥梁易损性的影响[3]。也有学者在截面设计优化方面进行了研究，孙洁等针对波纹钢腹板结合梁利用ANSYS建立了其有限元分析模型，对其横截面进行了多变量的优化分析[4];燕松波等以PC斜拉桥局部稳定性及受力性能为优化目标，以截面各部分尺寸为变量，研究了主梁箱形截面的局部设计优化[5]。但对刚构桥主梁截面设计优化的研究却寥若晨星。

结合上述研究成果，本文以河池至百色高速公路某施工段红水河特大桥预应力混凝土连续刚构桥为依托背景，基于GSL&PS-PGSA算法即基于生长空间限定与并行搜索的算法组合新机制，结合Midas仿真计算分析，对背景桥梁主梁截面进行设计优化分析。

1 工程概况

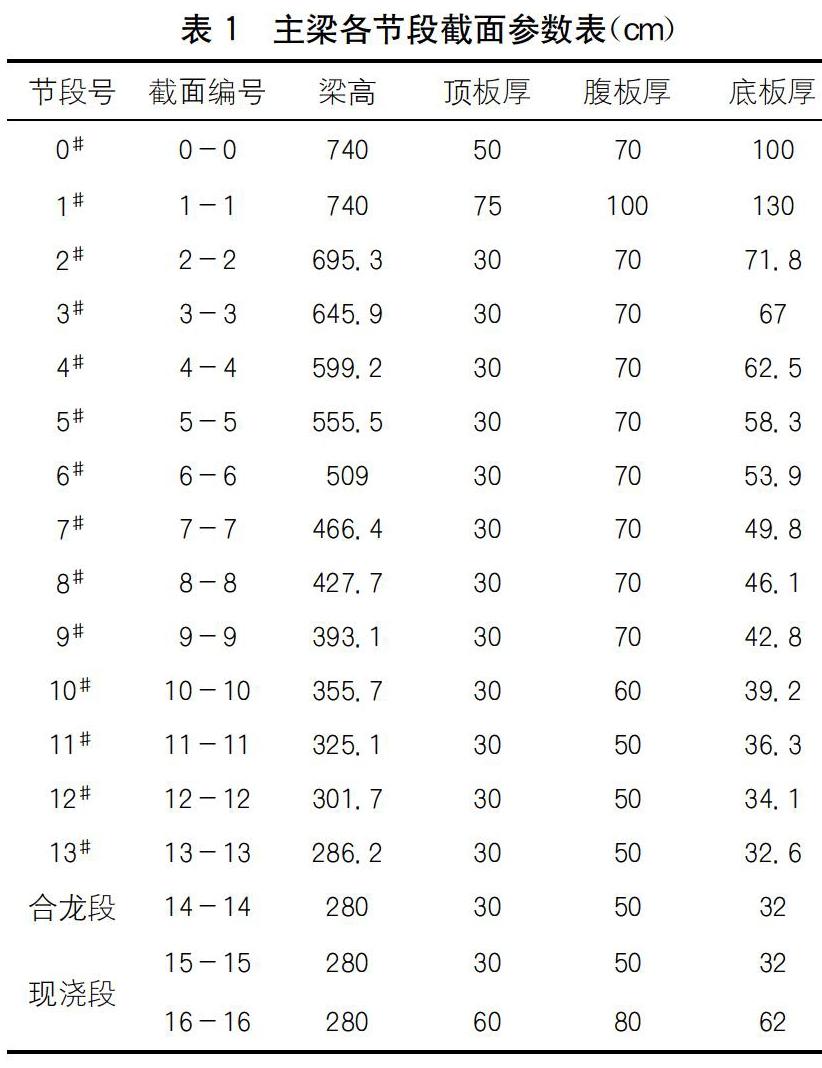
本文以河池至百色高速公路某施工段红水河特大桥预应力混凝土连续刚构桥为研究背景，桥跨布置为（65+2×120+65）m，箱梁为单箱单室直腹板截面，顶板宽12 m，底板宽6.5 m，翼缘板悬臂长2.75 m，墩顶截面梁高为7.4 m，跨中截面梁高2.8 m，高跨比为1/42.86，底板厚度及主梁截面高度均按1.8次抛物线变化。采用挂篮悬臂浇筑施工，0 #块长7.7 m，边中跨合龙段为2 m，边跨现浇段长3.88 m，悬臂现浇梁段最大重量为206.7 t，主梁总重为13 335.92 t。下部结构采用等截面实心矩形双支薄壁墩，横向尺寸为6.5 m，壁厚1.6 m，双壁间距为6.1 m，在墩高1/2处设置两道1.5 m×1.5 m的横系梁。主梁采用C55混凝土，桥墩采用C40混凝土。主梁各节段截面参数见表1。

2 基于GSL&PS-PGSA算法的设计优化模型

2.1 GSL&PS-PGSA算法基本原理

PGSA（模拟植物生长算法）以植物形态素浓度理论即其向光性机理作为启示准则，优化问题可行域即为植物的整个生长空间，将生长空间中的生长点作为优化问题的设计变量组合，优化问题的最优值则为离光源最近的生长点所对应的目标函数值[6-8]。其形态素浓度计算表达式如式（1）所示。

传统的PGSA优化算法步长单一，搜索机制不足，计算效率低，本文将采用融合并行搜索机制的GSL&PS-PGSA算法（基于生长空间限定与并行搜索的算法组合新机制）进行优化研究，其基本原理如下[9-10]：

（1）采用多种步长混合并行搜索方式，大步长负责距离较远新增可生长点的搜索，小步长负责所选生长点附近新增可生长点的搜索。

（2）在可生长点集合m加入新增可生长点更新集合前，先判断各新增可生长点对应的各目标函数值是否劣于集合m中最劣质的生长点目标函数值。剔除劣质可生长点，优质新增生长点加进集合m，增大了可行域跨度中优质可生长点的选中概率，也为算法提供了有效终止机制。通过劣质可生长点的剔除，控制集合m中可生长点个数上限为n个，提高了算法的计算效率。

2.2 刚构桥主梁截面优化模型

刚构桥悬臂浇筑施工过程结构受力复杂多变，无法用具体的显示函数对目标优化函数进行表达，多利用转换为抽象数学模型的方式对工程中优化问题进行解析，数学模型主要由目标优化函数minf（x）、优化设计变量x及优化约束条件Qi（x）三部分组成。

（1）目标函数：minf（x）

考虑刚构桥结构材料用量最优化问题，本文以主梁总质量作为目标函数minf（x），以目标函数最小值的问题去求解结构优化问题。

（2）优化设计变量：x∈X;x=（x1，x2，x3，……，xn）

通常取结构形状、结构截面特性等参数作为优化设计变量x，对于刚构桥主梁结构，考虑结构对称性，按其半跨节段纵向分29部分（包括悬臂现浇段、墩顶0 #块、边跨合龙段及边跨现浇段），取各节段截面编号为优化设计变量x。

（3）约束条件：Qi（x）≤0;i=1，2，3，……，m

一般以结构刚度、强度及稳定性等指标作为结构优化问题的约束条件。对于该刚构桥结构设计优化问题，取刚构桥在主梁混凝土施工过程中容许变形为约束条件1;强度设计值为约束条件2;稳定性为约束条件3。

2.3 刚构桥主梁截面优化流程

利用Fortran和Midas结合数据交互方式来实现基于GSL&PS-PGSA的刚构桥截面设计优化，具体操作流程如下所示。

（1）定义设计变量的初始组合即初始生长点x0，最大生长次数n，设计变量小步长step和步域比R。

（2）将初始生长点x0代入Midas中分析计算，提取分析结果，并计算目标函数值f（x0）。

（3）以当前次生长点为基点，设计变量大、小步长混合并行搜索当前次生长的新增可生长点，剔除重复或超出可行域的新增可生长点。

（4）将次生长中新增可生长点输出至Midas中进行结构分析，提取Midas的分析结果并计算目标函数值f（xm，j）;若f（xm，j）>fb（可生长点集合中最劣质生长点函数值），则剔除;若f（xm，j）

（5）判断可生长点集合m是否为空集，若否，则继续步骤（6）;若是，则转至步骤（13）。

（6）在当前次新增可生长点中找出最优目标函数值fmin，若fmin为当前最优值，则更新全局最优值Fmin及其对应的可生长点Xmin。

（7）按目标函数值优劣对可生长点集合m[WTBZ]中可生长点进行排序，并更新最劣值fb。

（8）判断可生长点集合中可生长点个数是否大于n，若是，则继续步骤（9）;若否，则转至步骤（10）。

（9）取较优的前n个可生长点，剔除其余可生长点，并转至步骤（11）。

（10）剔除函数值相对较劣的可生长点（按不低于95%的保证率）。

（11）根据式（1）对m[WTBZ]中所有可生长点计算其形态素浓度，并按概率随机挑选下一次生长的生长点。

（12）判断是否达到最大生长次数l，若是，则继续步骤（13）;若否，则转回至步骤（3）。

（13）提取最优目标函数值Fmin及其对应的可生长点Xmin并结束优化流程。

3 结构仿真模型的建立

为实现对连续刚构桥悬臂浇筑施工过程的精准模拟，采用仿真计算软件Midas Civil对依托工程红水河特大桥进行建模分析，定义桥梁纵向为全局坐标系的X轴，竖向为Z轴，横桥向为Y轴。结构共离散为291个节点，268个单元。采用固结约束模拟墩底固结，采用刚性连接模拟墩梁固结，采用活动铰支座模拟边支座;考虑节段循环悬臂浇筑进行施工阶段模拟，荷载考虑结构自重、挂篮、模板、人工机具及冲击、振捣等临时荷载。具体模型如图1所示。主梁各节段重量信息表如表2所示。

4 刚构桥主梁截面设计优化分析

根据刚构桥主梁施工方法及其受力特性，现按主梁施工顺序将主梁截面纵向分为29组作为设计变量的数目，每组截面顶底板及腹板按各节段分别设置不同厚度。根据参考多座同类型相似规模刚构桥主梁截面，选取各组截面顶底板及腹板厚度范围如表3所示。

以每组刚构桥主梁节段的截面编号作为设计变量;优化目标为刚构桥主梁结构总重;以主梁在施工过程中的挠度、应力、稳定性及各节段截面顶底板、腹板的厚度范围作为约束条件，其中挠度、应力限值及结构稳定性均根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG 3362-2018）中对应规定进行取值或计算。基于GSL&PS-PGSA利用Midas计算分析模型对主梁截面进行优化分析，各节段初始截面按表1中原设计各参数取值，主梁结构初始总重为13 335.92 t。

4.1 主梁截面设计优化结果

刚构桥主梁截面设计优化后，主梁结构总重为12 198.3 t，相较于优化前减少了8.5%;主梁在施工过程中，最大上挠值为30.28 mm，最大下挠值为54.33 mm;顶板最大拉应力为0.23 MPa，最大压应力为12.44 MPa;底板最大拉应力为0.44 MPa，最大压应力为10.88 MPa;均满足《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG 3362-2018）中相关规定要求，即均满足约束条件。具体每组各节段截面优化结果如表4所示。

4.2 优化前后结果对比分析

4.2.1 优化前后应力结果对比

主梁截面设计优化前即优化的初始状态，根据Midas计算结果，主梁截面优化前后应力结果如表5所示。优化前后主梁顶板最大拉应力由0.27 MPa变为了0.23 MPa，最大压应力由13.97 MPa变为了12.44 MPa;主梁底板最大拉应力由0.52 MPa变为了0.44 MPa，最大压应力由12.50 MPa变为了10.88 MPa;最大变化幅度为-16%。优化前后施工过程中主梁顶底板最大应力结果均满足约束条件。具体主梁施工过程中顶底板最大应力优化前后对比曲线如图2所示。

4.2.2 优化前后变形结果对比

表6给出了优化前后施工过程中主梁各节段最大变形结果，优化后主梁施工过程中各节段最大上挠值由39.33 mm变为了30.28 mm，减少了23%，优化后主梁施工过程中各节段最大下挠值由73.42 mm变为了54.33 mm，变化幅度为26%。优化前后主梁变形结果也均满足约束条件。优化前后主梁各节段最大变形对比曲线如图3所示。

5 结语

本文基于GSL&PS-PGSA算法，结合Midas仿真模拟计算，以河池至百色高速公路某施工段红水河特大桥为依托背景，以刚构桥主梁自重为优化目标函数对主梁截面设计进行了优化分析，主要结论如下：

（1）刚构桥主梁截面优化后，主梁结构自重由13 335.92 t降为了12 198.3 t，相较于优化前减少了8.5%，大幅度提高了主梁用料的经济合理性。

（2）刚构桥主梁截面设计优化后，施工过程中，主梁顶板最大拉应力减小幅度为16%，主梁底板最大拉应力减小幅度为16%;主梁顶板最大压应力减小幅度为10%，主梁底板最大压应力减小幅度为13%;优化后主梁截面应力明显减小。

（3）刚构桥主梁截面设计优化后，施工过程中，主梁最大上挠减小了26%，主梁最大下挠减小了23%。主梁各节段变形有明显改善。

参考文献：

[1]胡 斌，李庆择.灰色预测在大跨径刚构桥施工线形监控中的应用[J].铁道建筑，2020，60（5）：38-42.

[2]闫维明，罗振源，许维炳，等.近断层脉冲型地震动作用下高墩连续刚构桥振动台试验研究[J].北京工业大学学报，2020，46（8）：868-878.

[3]张炳鑫，郑史雄，杨 进，等.梁端碰撞效应对大跨高墩连续刚构桥易损性影响[J].铁道科学与工程学报，2020，17（4）：891-899.

[4]孙 洁，刘 磊，彭 益.波纹钢腹板简支结合箱梁的截面优化[J].铁道标准设计，2012（4）：61-62，69.

[5]燕松波，李伟平，蔡锁德.PC斜拉桥主梁箱形截面优化设计研究[J].公路与汽运，2016（3）：154-157，186.

[6]胡 苏，苏庆田，吴 冲.正交异性钢-混凝土组合桥面板截面优化研究[J].结构工程师，2015，31（2）：131-137.

[7]石开荣，阮智健，姜正榮，等.模拟植物生长算法的改进策略及桁架结构优化研究[J].建筑结构学报，2018，39（1）：120-128.

[8]石开荣，潘文智，姜正荣，等.模拟植物生长算法的结构优化新机制[J].华南理工大学学报（自然科学版），2019，47（7）：40-48，57.

[9]吕俊锋.基于改进PGSA的高层悬挂结构优化设计方法及施工模拟分析[D].广州：华南理工大学，2018.

[10]石开荣，潘文智，姜正荣，等.基于GSL&PS-PGSA的空间结构优化方法[J/OL].建筑结构学报：1-11[2020-07-19].https：//doi.org/10.14006/j.jzjgxb.2019.0640.