考虑回水影响的河道水位流量关系确定方法

孙昭华,周歆玥,范杰玮,熊海滨,谈广鸣

(武汉大学水资源与水电工程科学国家重点实验室,湖北 武汉 430072)

近20余年来,气候变化引发全球水旱灾害频发,除水文因素之外,上游建坝、大规模航道整治、河漫滩植被孳生、岸线开发利用等引起的河道地貌和水力因素调整起到了推波助澜的作用。Graf[1]、Slater等[2]、Slater[3]、Jemberie等[4]对欧美上百条河流资料的分析表明,人类活动干扰之下,河流主槽下切的同时,也出现了洪水河槽萎缩、河漫滩减小和洪水位抬升现象。准确辨识河道调整引起的水位变幅,是防灾减灾的基础。水文观测具有几十年甚至上百年的延续性,为河道调整判别提供了可靠数据,但如何利用测站水位—流量关系反演河道水力特性变化,始终是面临的关键问题之一[4- 5]。

完整的圣维南方程无解析解,河道水位—流量关系仅能通过简化函数式、经验曲线或其他间接映射关系描述,尽管这些方法形式各异,但总体可分为单值型和多值型关系两类。单值型关系中,测站断面的流量与水位一一对应,基于曼宁、谢才或堰流公式均可导出。这类关系式应用广泛,也不断得到改进,如Jemberie等[4]认为将流量取对数后再与水位建立多项式,可减小洪水流量下的水位误差,然后以此估算了150年来密西西比河河道调整引起的水位变化；James[6]用多年水位—流量数据拟合平均关系线,以计算水位与实测水位的残差来描述American River在90余年内的河床下切进程；Hasanpour Kashani等[7]尝试用智能算法建立水位—流量映射关系,相比传统的定线方法明显提高了精度。但应该看到,单值型关系中隐含了恒定均匀流的假定,导致两方面缺陷:一是天然河流中普遍存在的涨落水或回水顶托导致的绳套型关系无法反映,河床调整的影响可能被来流过程引起的水位波动所掩盖;二是测站水位变化是由当地局部调整引起,还是更下游的长河段冲淤引起,无法归因。

多值型关系考虑了涨落率、回水等因素影响,更符合河道水流运动规律,常见做法是在单一平均线之外再考虑一个修正因子,依据辅助水尺获取比降,形成以比降为参数的修正因子经验曲线[8- 10]。凭借率定好的经验曲线族,使用者只需水位观测值便可换算流量,从而降低流量观测的难度,中国和美国地质调查局(USGS)的规范中都推荐采用类似方法[9- 10]。但需指出的是,比降修正法是在河槽顺直、河底平坦的简单情况下导出的半经验方法[9],在宽窄相间、深泓起伏的天然河流中,需要长期经验累积并不断修正相关曲线族,才能保证精度[10- 11]。由于是为流量预报和整编服务,函数关系隐含在经验曲线中,反函数不易确定,借此估算特定流量级下的水位时仍存在困难。为降低经验性,Yen和González- Castro[12]提出采用河道水力特性图(Hydraulic Performance Graphs,HPG)来定量描述上下游水位和流量关系,在国外得到广泛推广[10- 11,13]。然而,HPG的建立需开展各种情况下的水面线计算,河道地形、糙率是必须的基础资料[10- 13],在很多情况下难以获取,并且水位—流量函数关系只能被隐含在图形中这一缺陷仍然存在。如何仅凭借水文观测资料,通过便捷的方式建立以流量反推水位的多值型水位—流量关系,仍值得研究。

三峡水库运行以来,长江中游河床调整引起的洪枯水位变化引起了广泛关注,但现有研究无一例外采用了单值型水位—流量关系,由此确定的水位变幅存在不少争议[14- 16]。长江中游比降平缓,沙市至九江近700 km的河段内水位都会受到通江湖泊和支流入汇顶托,消除回水影响才能厘清河床调整引起的水位变幅。此外,三峡坝下游冲刷沿程分布不均,当地和下游河段冲刷的影响本质上也反映在回水效应上,目前研究对此鲜有区分。针对这些问题,本文分析长江中游的河道水力特点,尝试改进和提出考虑回水顶托的水位—流量关系确定方法,并以此估算典型河段的水位变幅。

1 研究思路及研究资料

明渠一维水流运动由圣维南方程描述,在不同情形下,方程各项的主次地位皆可不同[11,13],试图用普适性方法描述各种情况下的水位—流量关系极为繁琐,甚至不现实,各种文献和规范中多建议采用不同简化方法[9,11]。本文的研究背景是长江中游这种大型冲积河流,其显著特点包括:①比降平缓,流动状态为缓流且明显处于阻力平方区,阻力随水位涨落和床面沙波消长而变[17]；②断面形态沿程虽不规则,但经由长期冲积过程塑造,存在明显的水力几何关系,过水面积、水深、河宽之间存在显著相关性[18]；③水位、流量的年内、年际波动虽有随机性,但长期来看又稳定在一定范围,上下游流量、水位的组合有一定规律可循。有鉴于此,提出本文研究思路:首先,考察已有常用方法是否适用于评估长江河道调整带来的水位变化；其次,结合长江中游河道水力特性,基于水力学及河流动力学原理对已有方法改进,检验新方法的有效性；最后,应用新的方法评估典型河段的水位变化特征。

多值型水位—流量关系涉及上下游2个测点(站),考察其影响因素需以站点之间的河段为对象。选取长江中游沙市—新厂(沙—新)、监利—城陵矶(监—城)、螺山—汉口(螺—汉)3个典型河段(图1),其中沙—新河段长64 km,属微弯分汊河型,汛期受洞庭湖出流顶托影响；监—城河段长约87 km,属典型弯曲河型,汛枯期均可受到洞庭湖出流顶托影响；螺—汉河段长约200 km,属江心洲分汊河型,汛期受汉江和鄱阳湖汇流顶托影响。需指出的是,监—城、螺—汉河段分别在河段出口存在汇流,但汇流点紧邻出口水位观测点,汇流对河段流量的影响近似忽略。

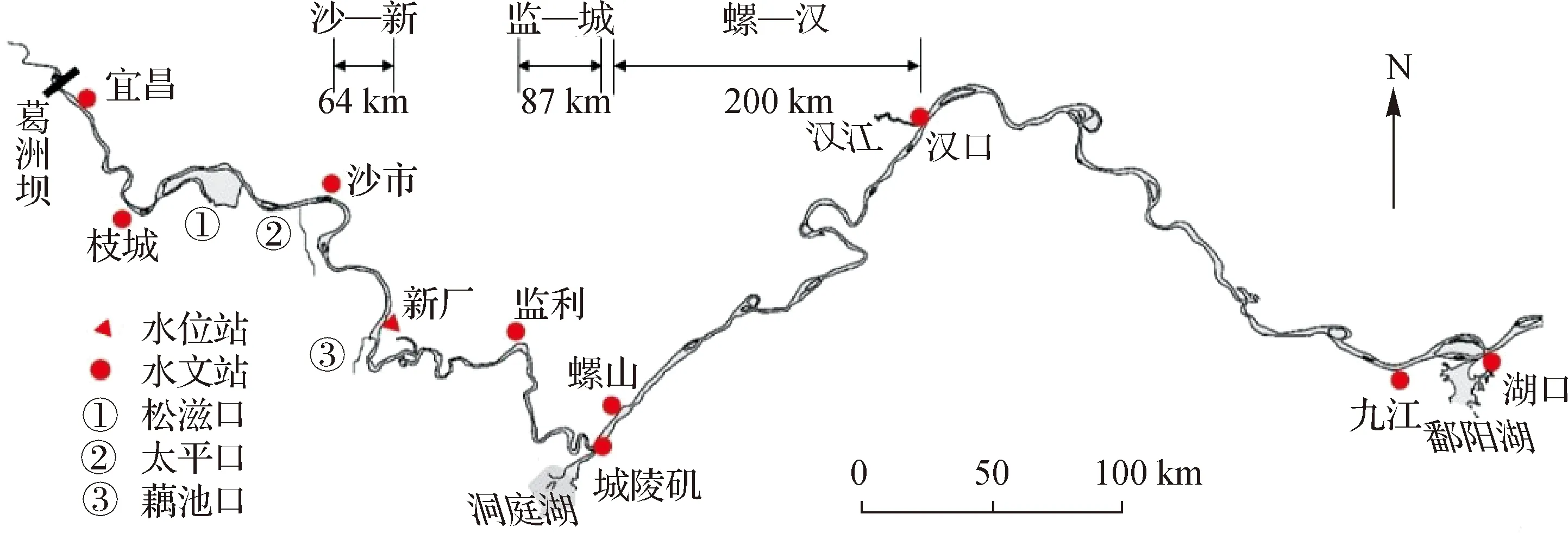
图1 研究涉及的水文站点与典型河段位置

经历了荆江裁弯、葛洲坝枢纽建设运行引起的河床调整,长江中游自1990年后逐渐进入稳定期,2003年后又进入三峡水库运行后的剧烈冲刷期[19- 20]。为反映各时段内洪枯水位变化,选取了研究河段各站全年逐日水文资料开展分析,资料年限为1991—2017年,其中1991—2002年代表天然准平衡时期,2003—2017年代表河床调整期。除此之外,还收集了长江委水文局布设的沿程固定断面地形资料,为2002年10月测次,3个河段内断面个数分别为43个、45个、96个。依据这些断面资料建立一维水流数学模型,以1991—2002年各河段进出口的平均水位—流量关系计算各级恒定流水面线,反推得到沿程过流面积、阻力系数等特征量,用以分析河道几何形态、阻力系数等要素随流量级的变化。

2 已有水位—流量关系确定方法在长江中游的适用性

2.1 常用的水位—流量关系确定方法

(1) 工程实践中应用最广泛的单值型水位—流量关系形为[5- 7,9]

Q=a(Z-Z0)b或Z=(Q/a)1/b+Z0

(1)

式中:Q为流量；Z为水位；Z0在特定断面为常数；a、b为待定参数。式(1)的物理本质是恒定均匀流,Z0对应0流量时的水位,一定程度上可反映河底高程[7]。式(1)的优点在于,可通过最小二乘法便捷确定参数,流量和水位之间可双向换算。

(2) 对于明显受回水影响的河段,中国和美国USGS的规范中均推荐如下式的关系[9- 11]:

(2)

式中:Qn、Qref分别为特定水位下的待求流量和某一参考基准流量；ΔZn、ΔZref为与Qn、Qref相应的落差,由基本水尺与其下游辅助水尺的同时刻观测水位得到；c、d为参数。式(2)基于恒定非均匀渐变流得到,在河底平坦、断面规则的理想情况下,c为1,d为0.5,但天然河流中的形态一般不规则,式(2)常被事先绘制成经验曲线族。式(2)的优点在于,能体现回水影响,其不便之处在于需要参考基准流量以及各种辅助曲线,在不规则河道上需要较多经验,难以通过流量推算水位。

(3) 出于推算河道水位和泄洪能力的需求,Yen和González- Castro[12]提出用HPG描述河道水力特性,其思路是:河道首末端水位Zu、Zd与流量Q之间存在Zu=f(Q,Zd),推算各种可能的Q和Zd组合下水面线,以Q为参数将所有(Zu,Zd)数据对纳入同一坐标平面并连线,即得到HPG。图2是缓流情况下的HPG示例,其中L线代表了水面为水平的极限情况(Zu=Zd),N线代表沿程均匀流情况,Cd线对应下游端为临界水深的极限情况。理想情况下N线与L线平行,与横轴夹45°角,两者在横轴截距相差i0L(i0与L分别为平均河床比降和河段长度)。N线所分成的M1区、M2区分别对应壅水和跌水2种情况。HPG直观地归纳了河道内水力关系,其缺点是图形制作需地形、糙率等资料,过程较繁琐。

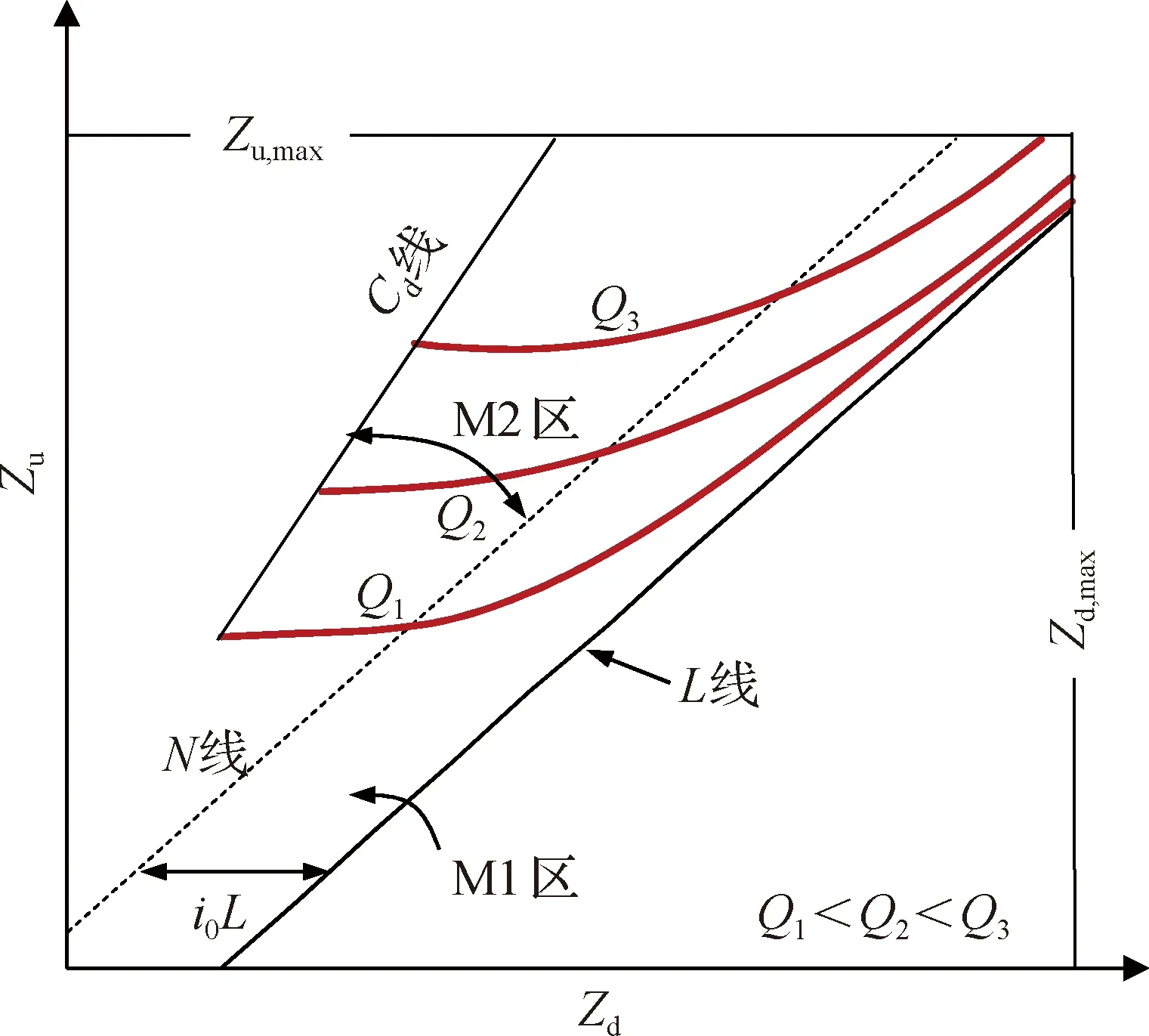
图2 缓流情况下HPG示意[12]

以上3种代表性的水位—流量关系模式均基于恒定流,且忽略了时变项。大量分析表明[10- 12],缓坡情况下沿程水深变化引起的压力项与河床坡降项量级相当,而惯性项与压力项的比值正比于弗劳德数平方(Fr2),量级较小,因此以上忽略时变项的近似是合理的。可以看到,河道的物理特性在几种模式中通过参数或辅助曲线得到保留,能够用于不同场合。

2.2 已有水位—流量关系确定方法的适用性分析

针对沙市、监利和螺山站,以式(1)拟合1991—2002年水位—流量关系如图3。可见,由于回水等因素影响,计算与实测水位存在残差(同流量下实测水位-计算水位),其中监利、沙市两站受洞庭湖出流顶托影响,水位残差具有汛期大、枯期小的特点,监利站最大将近±4 m,沙市站最大可达±1.7 m；螺山站水位残差汛枯期差异略小,同流量下变幅在±1.2 m。可见,不同水情下的水位—流量关系变幅较大,直接用单值型关系来估算水位存在较大不确定性,汛期尤为严重,其主要原因是由均匀流假定所致。

采用多年平均水位—流量关系结合河道断面地形,反推各级流量下3个河段内弗劳德数(Fr),结果表明枯期至汛期沙—新河段Fr变幅为0.11～0.20。监—城河段为0.11～0.17,螺—汉河段为0.08～0.14,量级均不大。因此,3个河段内水流运动时变项可忽略,式(2)或图2有其应用前提。图4给出1991—2002年3个河段内日均落差,可以看出各级水位下的落差围绕着多年均值波动,对应均值与变幅在沙—新、监—城、螺—汉河段分别为2.94×(1±30%)m、3.09×(1±60%)m、4.97×(1±20%)m。同一个河段内,虽然洪枯各级水位下的平均落差相差不大,但同一水位下的落差变幅较明显,尤其是监—城河段。根据式(2),若同一水位下落差波动60%,导致的流量变幅可超过26%,这说明在式(2)中引入落差参数非常必要。然而,由于参考流量Qref无法确定,式(2)仍无法根据流量估算水位。此外,式(2)中落差通常指基本水尺与辅助水尺之间的落差,两者相距几公里,该数值近似可代替基本水尺断面附近的局部比降[10]。但在几十甚至上百公里的2个水文站之间,长河段落差是否可代替水文站附近局部比降,尚无法确定,这更使得式(2)在长河段的应用缺乏依据。

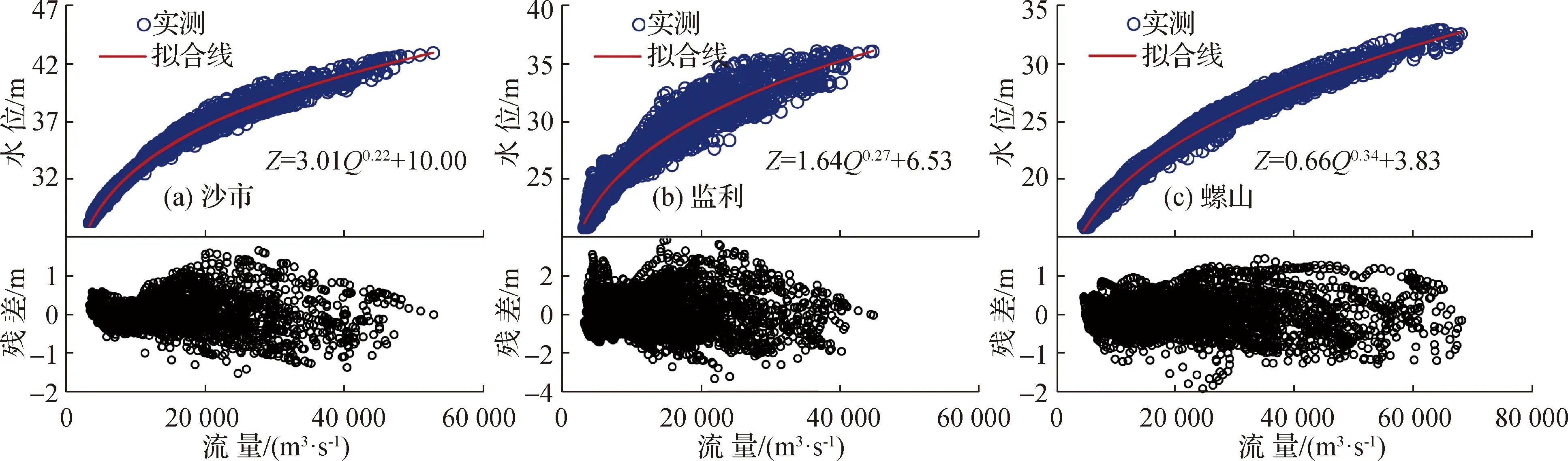
图3 单值型水位—流量关系及计算水位残差(1991—2002年)

根据Yen和González- Castro[12]方法,缺乏地形资料情况下图2中的HPG无法绘出。但图2的参考意义在于,它指出了均匀流情况下水位相关线(N线)的位置,并可判别壅水状态。根据Schmidt和Yen[11]的分析,即使在不规则河道内,也存在与长河段河床平均坡降相平行的恒定流水面线,定义为长河段的“正常流”。图4中长河段内特定水位级下的平均落差随水位变化并不大,本文将该落差均值近似视为“正常流”落差,其意义类似图2中的i0L。在此基础上,将图4中的落差均值指定为截距,以3个河段进出口实测水位拟合线性关系如图5,可见得到的直线斜率均近似为1,除监—城河段外,决定系数R2均在0.99以上。这说明图5中回归得到的直线近似于图2中的N线,同时也表明,河段内的流量和水位组合并非任意,而是在“正常流”附近小范围波动,体现了天然河道的水情特点。

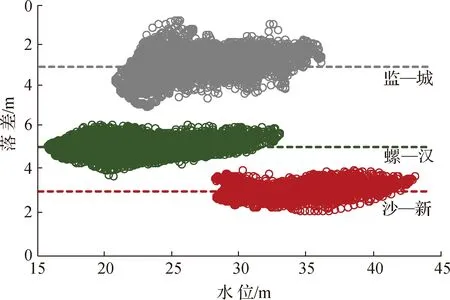
图4 河段每日进出口落差—进口水位关系(1991—2002年)

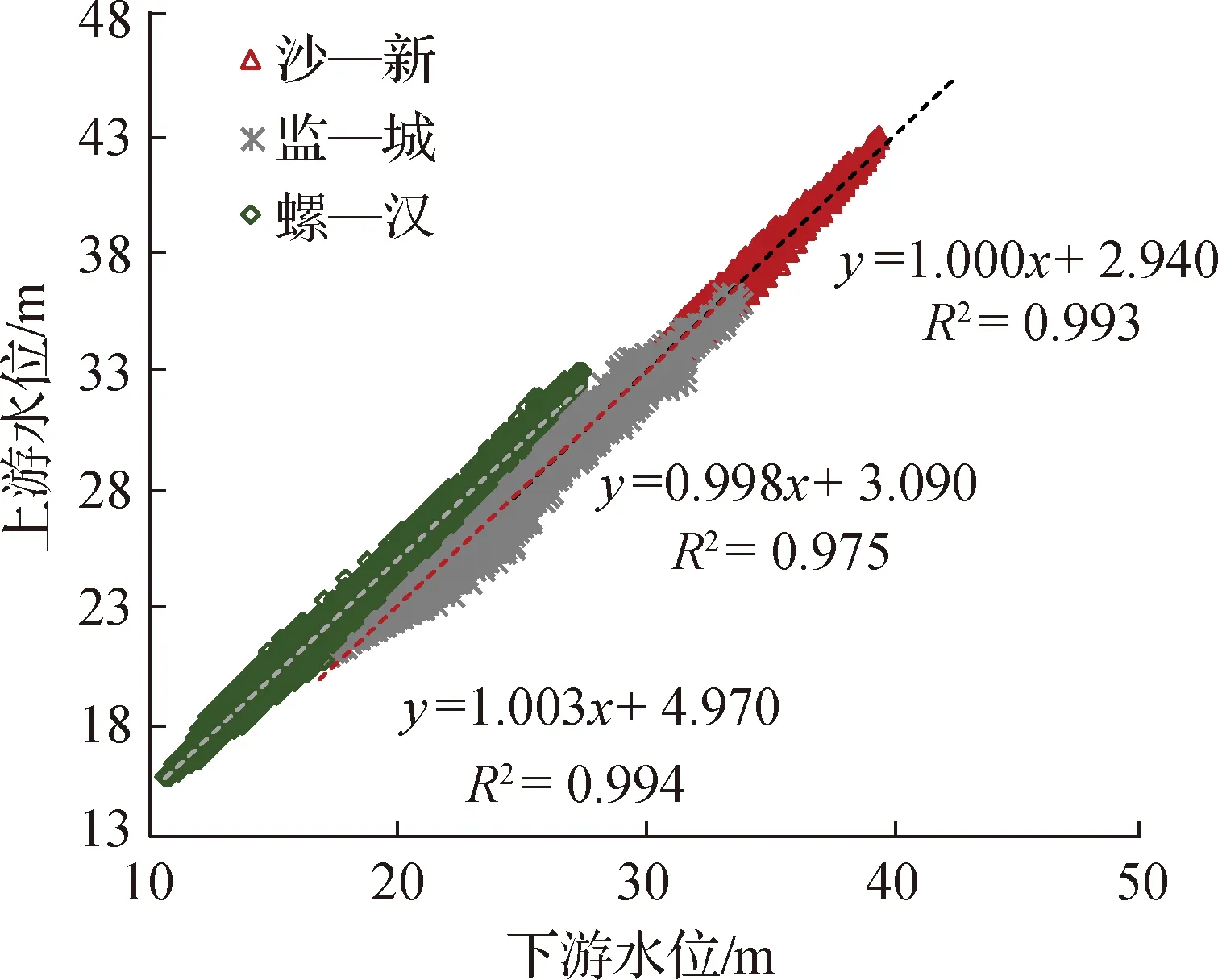
图5 河段进出口水位关系(1992—2002年)

3 水位—流量关系确定方法的改进与检验

3.1 方法改进的理论原理

考虑对式(2)进行改进,重点解决2个问题,一是分析用长河段落差代替进口水文站附近局部比降的可行性,二是探讨将参考流量表达为包含水位的函数式,从而可以根据流量反算水位。

忽略当地加速项之后,明渠恒定渐变流可用以下两式描述:

(3)

(4)

式中:C为谢才系数,C=h1/6/n,n为糙率系数,h为断面平均水深；A为过流断面面积；B为水面宽度；if为能坡。可见,能坡中包含了水深、河宽沿程变化的影响,在河床剧烈起伏或河宽沿程急剧变化的情况下,河道形态对能坡的影响不可忽视[11]。长江中游分布有较多天然抗冲节点,加之沿程洲滩密布,河道沿程呈现宽窄相间、深泓起伏的鲜明特点。但作为长期冲积形成的细沙河床,一般具有宽段水深小、窄段水深大的普遍特点。对3个典型河段内沿程各断面的h、B进行分析发现,固定流量下2个特征要素呈现良好的负相关性,形如式(5)。

h=αB-β

(5)

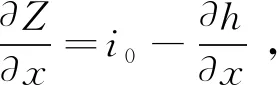
(6)

同级流量级下的糙率n沿程变化一般不大,由式(6)可见局部河段的比降仅与河宽有关。一方面,水文站一般设在宽度适中的位置,站点附近河宽与长河段内平均河宽相差不大；另一方面,在接近或超过平滩流量时β在0.6附近,B的指数接近于0。由这两点可知,只要河段长度不足以使糙率n沿程发生明显变化,进口水文站附近局部比降与长河段平均比降(Zu-Zd)/L近似,越是洪水期这个近似条件越成立。

将式(3)中的能坡以水面比降代替,并指定某个参考状态流量为Qref。在下游端水位调整使比降发生变化,而上游端水位保持不变的情况下,河段过流量可表示为

(7)

由图4和图5可见,河段内存在平均情况下的近似“正常流”状态,该种状态下(Zu-Zd)ref为定值,Qref可由式(3)或式(1)计算,将其代入式(7)后得到

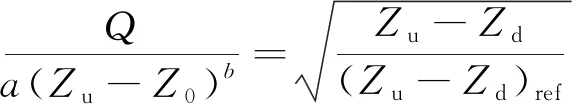
(8)

式中:参数a′为变换之后的参数；b′=2b。需指出的是,冲积河流中的糙率并非常数,而是随着流量涨落和水流条件强弱导致的床面形态而变[17],但由所率定的3个典型河段内不同流量下n值可见(图7),其与流量之间基本呈幂指数关系。若采用图7中的幂指数关系来完成式(7)到式(8)的推导过程,并不改变式(8)的形式,也即式(8)适用于动床糙率。

图6 典型河段内河宽—水深关系

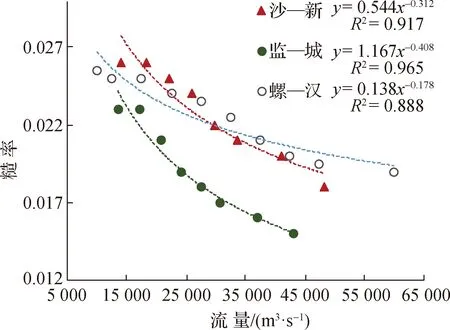
图7 典型河段内糙率—流量关系

基于长江中游河道形态、阻力和水情特点得到式(8),确定了Zu=f(Q,Zd)的多值型关系。据此可得

(9)

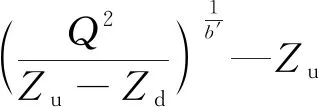
3.2 新方法的效果检验

相比于式(1),式(8)为隐函数,参数确定难度增加,在实践中是否具有可操作性需要检验。相比于图2中的HPG曲线,式(8)的确定过程仅需水文观测资料,直接依赖的数据类型少了河道地形、糙率等,这是否会导致河道水力特性物理信息的缺失和计算结果不合理,需要检验。

利用1991—2002年3个河段进出口日均水文数据,图8(a)中给出式(8)左右侧变量的相关关系,不断调整b′值并考察R2值,可得到其余参数(表1),操作较为简单。达到最优效果时,图8(a)中的R2值均在0.97以上。图8(b)中给出了式(8)计算水位与实测值的比较,即使对于水位—流量关系较散乱的监利站,R2值也在0.99以上。在概化为恒定渐变流的前提下,以上过程中并未考虑河段进出口相位差,即便如此依然取得了较好效果。式(8)和式(1)的计算效果比较如表1,由2种情况下的R2值可见,式(8)的水位计算精度明显更高。需指出的是,式(1)和式(8)中参数Z0的物理含义均是指流量为0时的水位,一定程度反映断面附近河床高程。由表1可见,式(8)中反算的Z0与真实河床高程较为接近,而式(1)的参数值差异较大。究其原因是由于式(1)假定沿程为均匀流,Z0更大程度上表征了长河段河床平均高程。由此可见,式(8)物理意义更为明确。

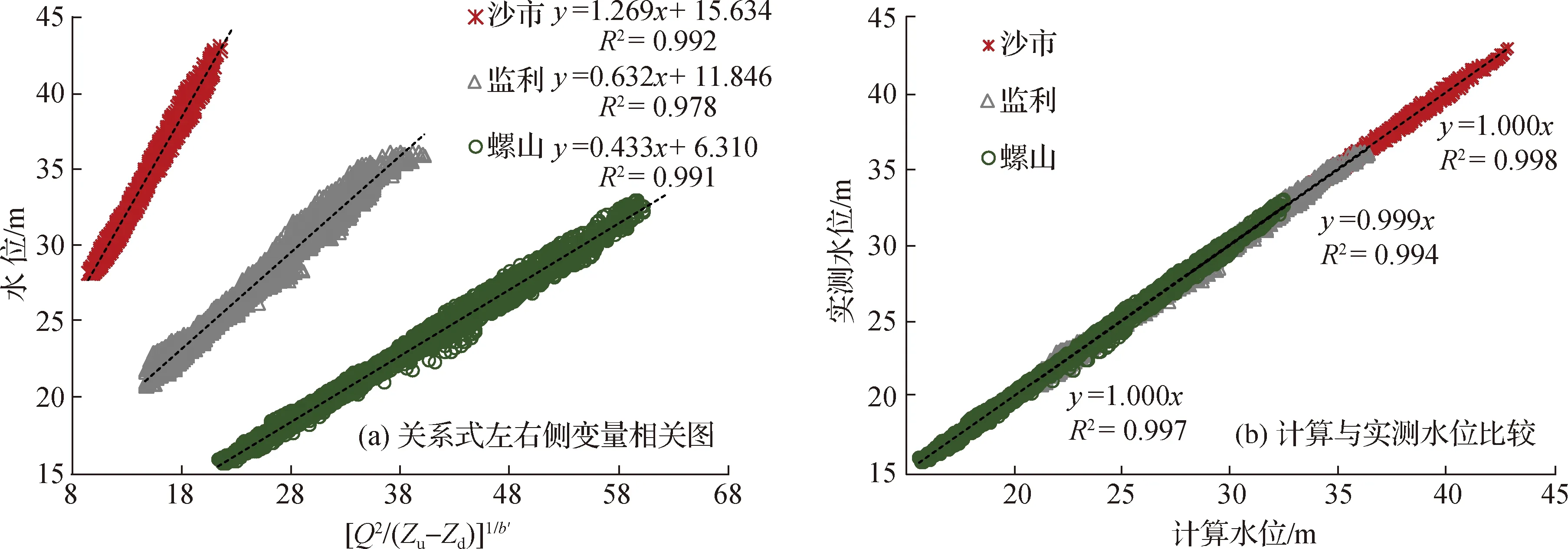
图8 式(8)的参数率定效果和计算效果

表1 式(1)和式(8)的参数及计算效果比较

以监利站大水年1998年为例,图9中给出了依据式(1)和式(8)计算的水位过程,2种模式下均采用了1991—2002年资料率定的平均关系。由图9可见,式(8)的计算结果重现了洪水涨落过程中的明显绳套过程,而式(1)不具此功能。1998年汛前江湖底水位高,图9显示监利站中洪水位整体比多年平均线明显偏高。同样以监利站为例,依据多年的来流和河段出口(城陵矶站)水位变化范围,仿照图2考虑多种组合,以式(8)计算绘制HPG如图10,图中的N线用图5中的水位相关趋势线代替。可见,仅凭借水文资料也可得到与图2类似的曲线,并且该曲线族覆盖了三峡水库运行前后的1991—2002年、2016—2017年实测水位变化范围。这说明,经准确率定参数之后,河道地形、糙率等因素的综合作用已被参数所涵盖,基于水文资料的式(8)与基于河道地形的图2具有类似物理含义。

图9 1998年监利站实测与计算水位过程

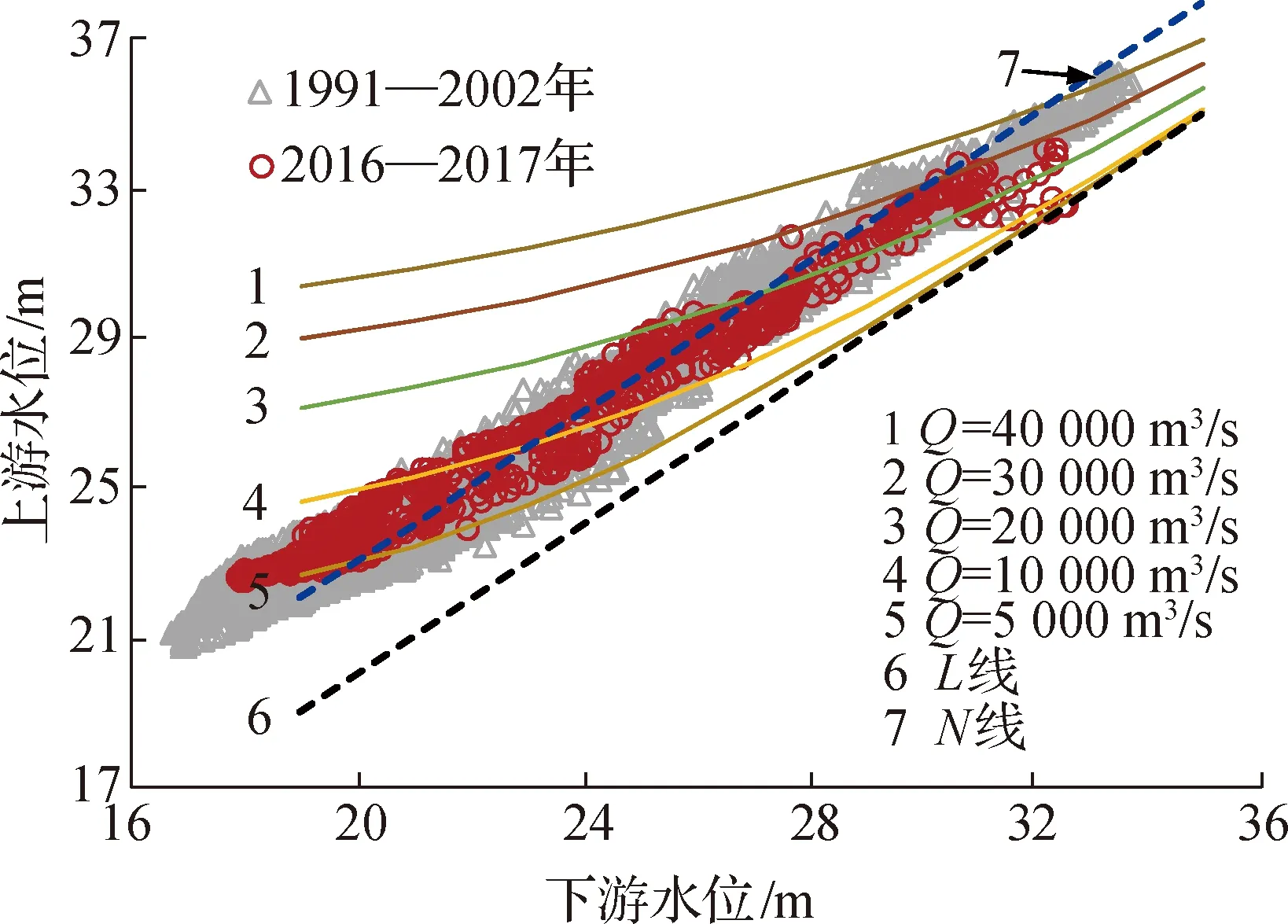
图10 监利站实测水位与计算HPG图比较

4 新方法在典型河段水位变幅估算中的应用

4.1 水位变幅估算的方法步骤

即使在天然准平衡条件下,由于年际间水沙波动,河道地形和糙率引起的水位微幅调整也不可避免。为区分噪声和趋势性变化,采用以下方法步骤:

(1) 以1991—2002年水位—流量拟合多年平均关系式(8),将1991—2017年各典型河段进口实测流量Q和下游实测水位Zd代入,得到Z的计算值系列；

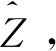
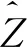
上述步骤中,若水位计算采用单值型关系式(1),则水位残差含义与James[6]的方法类似,以下将其称为模式1,本文方法称为模式2。

通过理论分析,可对水位残差的来源组成实施分解。恒定渐变流前提下,对应于流量级Q,河段进口水位可描述为Z=f(Q,Zd,G),其中Zd、G分别为下游水位和河床水力特性(形态与糙率)。采用模式1时,仅有流量Q为确定值,水位残差由Zd和G2种因素的不确定性导致,可表示为

(10)

式中:Zd,m、G分别代表均衡状态下Zd、G的期望值,ΔZd、ΔG为2种因素的波动。若采用模式2,不仅流量Q为确定值,出口水位Zd也为已知,水位残差表示为

(11)

由式(10)可见,模式1条件下,下游水位波动和河道调整的影响相互交织,一方的趋势性变化易被另一方掩盖。而由式(11)可见,模式2条件下,水位残差中的下游水位波动的影响为小量,因而该方法能够使河道调整的影响得以凸显。

4.2 不同河段水位变幅计算分析

分别选取洪枯水流量级,图11中给出了各站的固定流量级下水位残差变化。由图可见,对于枯水流量级而言,沙市、监利和螺山3个站均显示了下降趋势,沙市站的下降趋势始于2003年,监利站始于2010年,螺山站始于2012年,至2017年模式1显示的3个站降幅约为2.5 m、1.1 m和1.3 m,模式2显示的则为1.7 m、0.5 m、1 m。对于洪水流量级而言,3个站均未显示出明显变化趋势。

模式1和模式2的计算结果,分别体现了综合变幅和河段内调整引起的变幅,两者的差异主要由出口水位变化引起,通过这种方式可将本河段内河床调整的影响和下游站以外的影响加以分离。由图11可见,2种模式下的枯水位残差变幅在河床调整情况下均存在明显差异,若考虑沙—新、监—城和螺—汉河段的长度和河道调整历时差异,则河床调整对枯水位的影响分别为0.177 cm/(km·a)、0.072 cm/(km·a)、0.076 cm/(km·a),上荆江的沙市站受河道调整影响最为明显。因此,对于水位降幅明显的河段,采用本文的方法可分离本地河段和下游站之外的影响,而对于像监利站这样的年际水位变幅较大的受顶托站点,采用以往方法很难识别出水位变幅(图11(c)),而本文方法去除回水因素之后,趋势性变化更易识别。

图11 各站洪枯水位变幅(1991—2017年)

由图11还可看出,采用模式1,洪水流量级下的水位残差波动非常大,相比于枯水位更难看出变化趋势,甚至一些年份受水文波动引起的回水影响,易造成水位抬高的错觉。例如图11(f)中显示的2010年与2016年,受螺山至大通之间区间来水较大影响,汉口水位对螺山水位产生明显顶托,如果以模式1或者常规的水位—流量关系直接对比方法(图12),都显示同流量下洪水位抬高。但若采用模式2消除回水影响之后,可见其水位残差基本在历年波动范围内。因此,采用本文方法判别水位变幅,更利于形成客观的认识。

国外一些研究曾建议用HPG估计河床调整的影响[10- 13],本文提出的式(8)与HPG具有等价作用,因而也可用于评估河道水力特性的变化。以监—城河段为例,分别用1991—2002年和2012—2017年资料率定式(8)中的参数以反映不同时期河道状态,比较2个时期同流量下的HPG曲线如图13。可见,图中曲线反映的水位降幅与图11类似,即流量越小、城陵矶水位越低时期,监利水位降幅越大,而流量较大或城陵矶水位较高时期,监利水位变幅不大。考虑到长江中游上下游水位组合一般在图2或图10的N线附近,也即与平均状态偏离不大,而在远离N线的位置因缺乏实测资料而参数精度难以保证,因此在长江中游更推荐使用距平残差方式估计水位变幅。综合而言,本文方法具有解析表达式,能够方便地计算水位残差,相比于HPG更具优越性。

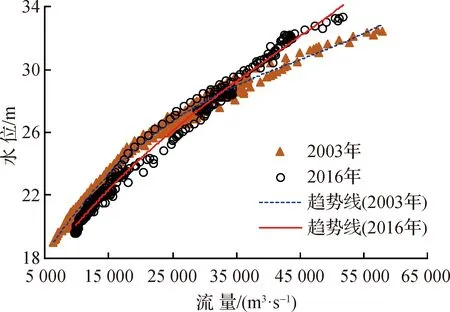
图12 螺山站2003年与2016年水位—流量关系

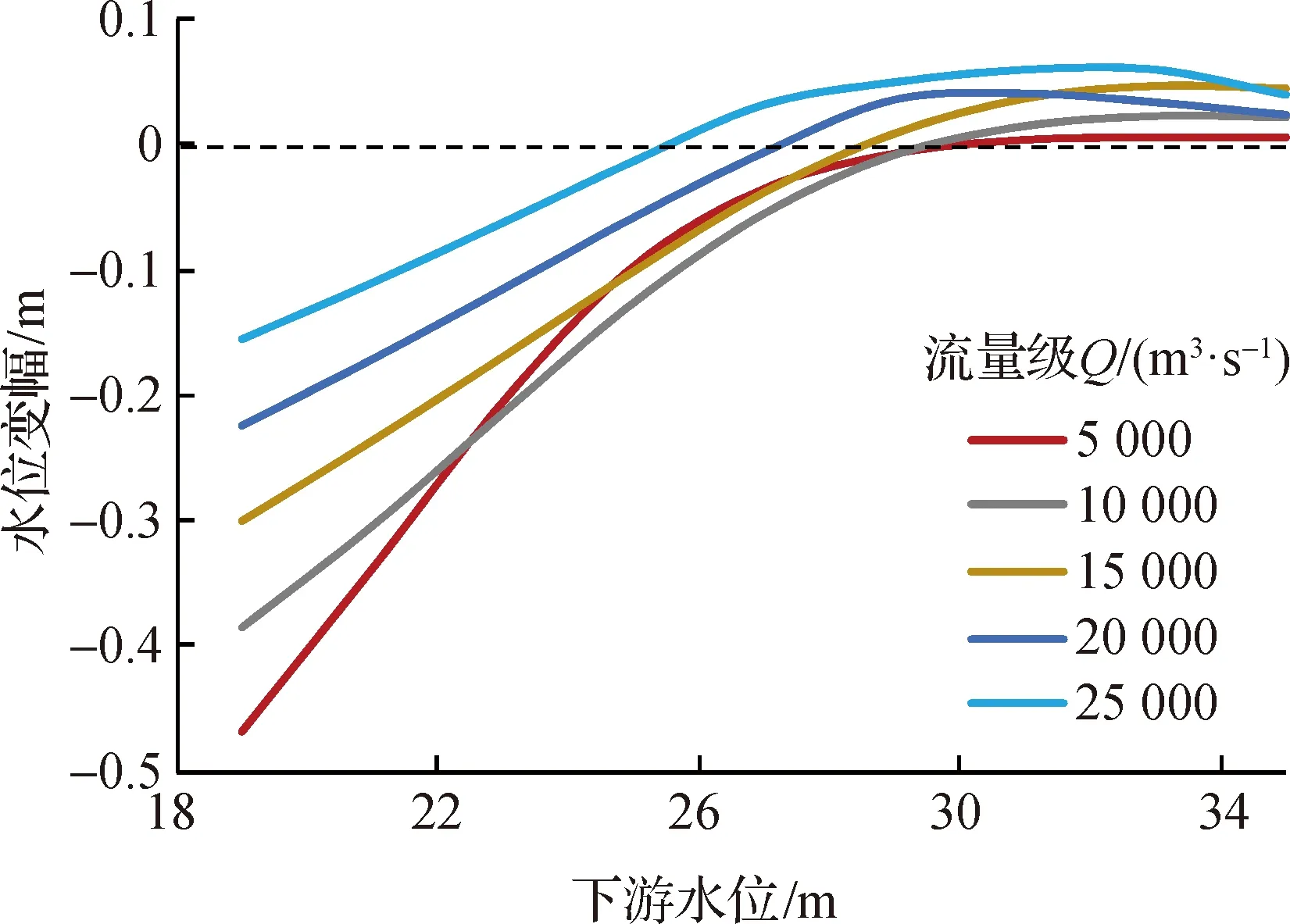
图13 三峡建库后监—城河段HPG曲线变幅

5 结 论

针对长江中游河床调整后水位变化趋势判别问题,比较了现有方法的优缺点、适用性,在分析长江中游河道水力特性的基础上,改进和提出了新的水位—流量关系确定方法,能够用来估算河床调整引起的各流量级下水位变幅。主要结论包括:

(1) 长江中游长距离内受回水顶托影响,采用单值型水位—流量关系估算水位变幅存在较大不确定性,而已有的多值型关系由于资料需求、函数表达形式等问题,无法直接用于水位变幅估算。

(2) 长江中游各级流量下弗劳德数小,沿程河道断面的宽、深形态因素具有良好制约关系,动床糙率与流量相关性好,根据这些条件简化恒定渐变流方程,可得多值型水位—流量函数关系。该函数关系仅依赖于水文站资料即可确定参数,在不同位置、不同河型的多个典型河段内均取得了较好的水位计算效果。

(3) 长江中游河段的各流量级水位落差一般维持在多年平均状态附近,可利用距平残差估算河床调整引起的水位变幅,本文方法消除了回水影响,河床调整的作用更易量化识别。

(4) 本文方法在典型河段的应用表明,长江中游枯水位明显下降,且各站的起始时间、幅度各不相同,但洪水位尚未有明显变化趋势,个别年份的洪水位偏高主要由回水引起。

许多冲积河流具有类似于长江中游的河道水力特性,本文的方法具有推广价值,只是其中的参数需结合具体河段资料率定。本文侧重于方法探讨,对长江中游水位变化规律和机制的系统分析还有待后续研究。