黄河下游动床阻力变化及其计算方法

夏军强,刘 鑫,张晓雷,周美蓉

(1. 武汉大学水资源与水电工程科学国家重点实验室,湖北 武汉 430072；2. 华北水利水电大学水利学院,河南 郑州 450011)

与一般的定床明渠水流不同,冲积河道的综合阻力一般有以下几方面组成:动床阻力(或称床面阻力),岸壁阻力,滩地阻力及河势(险工)阻力等,其中动床阻力是河道综合阻力的重要组成部分[1- 2],包含沙粒阻力和沙波阻力。动床阻力在冲积河道洪水演进与河床冲淤计算中具有十分重要的作用,水流条件与床面形态是影响动床阻力的主要因素,且床面形态又与水流条件紧密相关[3]。黄河下游水沙过程与床面形态复杂,不同水沙条件下的动床阻力变化较大。因此有必要研究黄河下游动床阻力的变化规律及其计算方法,从而准确预报下游洪水演进及河床冲淤过程,提高数学模型的计算精度。

现有黄河下游水沙数学模型中阻力计算主要采用2类方法:经验法和公式法。经验法通常先建立流量与糙率的经验关系,再根据冲淤厚度及床沙级配调整做一定的修正[4]。公式法则根据已有阻力公式直接计算。已有研究主要采用阻力分割法和综合阻力法建立动床阻力公式:① 阻力分割法,分别建立沙粒阻力和沙波阻力等阻力单元的计算公式。早期Einstein和Englund建立的阻力分割方法需要迭代试算,近年来Schippa等[5]和Niazkar等[6]均提出了不需要迭代和试算的阻力分割计算方法,但选取的参数与计算步骤都相当复杂。② 综合阻力法,直接建立综合阻力系数或床面当量粗糙度与水沙因子、沙波影响因子的经验关系。Wu和Wang[7]、Camenen等[8]均按照这个模式建立了相应的阻力公式,这类公式的难点在于选取合适的动床阻力影响因素。近年来,Azamathulla[9]和Roushangar等[10]利用人工智能、遗传算法和机器学习等技术构建了精度较高的阻力计算模式,但计算量较大,缺乏力学机理,难以用于数学模型。黄河下游动床阻力计算公式的研究成果也很多,李昌华和刘建民[11]收集了黄河、长江及赣江等河道的实测资料,得出了阻力系数与相对流速的经验关系;秦荣昱等[2]将糙率系数的变化归结为卡门常数的改变,提出了黄河下游糙率系数的计算公式;赵连军和张红武[12]引入摩阻厚度和涡团参数,建立了适用于黄河下游的动床糙率公式。这些阻力公式的率定及验证均采用小浪底水库运行前的实测数据,近期黄河下游动床阻力变化特点与计算方法的研究还未深入开展。

不同床面形态下的阻力相差很大、变化规律也不一致,因此床面形态判别对动床阻力计算有重要意义。黄才安和王进[13]引入了无因次床沙粒径,提出了床面形态判别的人工神经网络方法;张原锋等[14]基于床面形态控制数理论,建立了黄河下游床面形态的判别方法;白玉川等[15]提出了通过反演阻力规律表达式区分床面形态的方法,并得到了高、低能态时不同床面形态分区之间的分界线方程;在判别不同床面形态的基础上,Brownlie[16]选用沙粒弗劳德数(Frd)、床沙中值粒径(D50)与黏性底层厚度(δ)的比值及水力坡度(J)来确定水流能态区;王士强[17]和Karim[18]通过建立沙粒弗劳德数或弗劳德数(Fr)与相对水深(h/D50)之间的关系来判断水流能态区。尽管床面形态判别方法的研究取得了一定的进展,但由于影响床面形态的因素较多,且野外观测难度较大、实测资料有限,现有研究成果还不足以精确划分动床阻力的不同水流能态区。黄河下游床面形态的变化是影响阻力计算精度的重要因素,因此建立基于水流能态分区的动床阻力公式很有必要。

基于前人研究成果,本文收集黄河下游1958—1990年各水文站的实测数据,分析影响下游河道动床阻力的主要因素,分别选用直接建立动床阻力公式和先进行水流能态分区再建立对应于各水流能态区的动床阻力公式2种方法,提出不考虑水流能态分区和基于水流能态分区的黄河下游动床阻力公式,利用黄河下游1991—2016年的实测数据对基于水流能态分区的动床阻力公式进行验证。

1 黄河下游基本情况

1.1 河段概况

黄河下游具有上段宽下段窄、上陡下缓、上段冲淤变化大、下段较为稳定的特点[19]。按河型及其演变特点不同,黄河下游河段依次可分为3个不同河型的河段:游荡段、过渡段和弯曲段,如图1所示。黄河下游自孟津至高村河段为典型的游荡型河段,河段总长为275 km,河床纵比降为0.17‰～0.26‰；该河段河床宽浅,两岸堤距一般为5～20 km,河槽宽为1.0～3.5 km,滩地面积远大于主槽面积,约占河道总面积的80%以上。高村至陶城埠河段长约155 km,为游荡型向弯曲型发展的过渡型河段,河床纵比降约为0.12‰,两岸堤距1.0～8.5 km,主槽宽度约为0.5～1.6 km。陶城埠至利津河段长约301 km,为弯曲型河段,河床纵比降约为0.1‰；两岸堤距0.5～5.0 km,平均主槽宽度约为0.4～1.2 km；该河段两岸险工、控导工程较多,防护河段长度占该河段总长的70%,其主要河湾都得到了控制[3]。

图1 黄河下游河道示意

1.2 水沙条件及冲淤过程

黄河下游通常水少沙多,河道长期处于淤积抬升状态,尤其是游荡段两岸堤距较大、河道宽浅,泥沙淤积严重[20]。小浪底水库运用后,黄河下游水沙条件变化显著。花园口水文站实测水沙资料统计(图2(a))表明:小浪底水库运用前(1986—1998年)、运用后(1999—2016年)下游多年平均水量分别为282.1亿m3/a、251.4亿m3/a,后者减少了10.9%；多年平均沙量分别为7.60亿t/a、0.83亿t/a,后者减少了89.0%。因此小浪底水库运用后,进入黄河下游的水量有所减少,沙量大幅度减少。来沙量持续减少使得黄河下游由原来的累计淤积状态转为持续冲刷状态。据统计,1999—2016年间,黄河下游河段总冲刷量为19.11亿m3,其中游荡段的冲刷量占72%(图2(b))。

图2 1986—2016年黄河下游水沙变化及河床累计冲淤过程

2 动床阻力及其影响因素分析

黄河下游河段为典型的冲积性河道,断面形态宽浅,尤其在游荡段,综合阻力主要为床面阻力[25- 26]。为揭示黄河下游的动床阻力变化规律,收集并整理黄河下游各水文站的实测资料,在此基础上分析动床阻力的主要影响因素,进而确定影响黄河下游动床阻力的关键水沙因子。

2.1 动床阻力数据整理

收集了黄河下游1958—1990年的1 000多组与动床阻力相关的实测数据,数据均源于花园口、高村、利津等7个水文站。根据流量测验规范,水文站所在河段通常要求相对顺直匀整,水流集中,且河宽、水深等参数均无明显纵向变化,因此可以认为这些实测数据接近均匀流条件。在实际计算中,动床阻力通常采用实测资料,根据式(1)反求糙率系数和达西- 韦斯巴赫阻力系数。虽然糙率系数是综合阻力系数,但对于黄河下游这种宽浅型河道而言,综合阻力主要由动床阻力组成[21- 22],本文近似认为两者相等。

(1)

式中:n为糙率系数；f为达西- 韦斯巴赫系数；R为水力半径；J为能坡,采用水面纵比降近似替代；U为断面平均流速。由于受到测量条件的限制,这些实测数据不能全部用于动床阻力分析。为提高率定结果的精度,对实测数据按以下原则进行筛选:

(1) 实测资料中每组数据须包含流量、河宽、水深、比降、床沙级配、水温、含沙量等水沙要素,如这些关键水沙要素的实测值有缺失,应剔除这些数据。

(2) 洪水漫滩后,水深沿横向分布极不均匀,导致实测糙率出现极小值,故应剔除大漫滩时的阻力数据以及实测糙率值小于0.01的不合理数据。

(3) 由于野外测量条件限制,容易产生测验误差,导致部分水力要素明显不合理。目前黄河下游水面纵比降多采用比降水尺法,即在测验断面上下游等距的地方设置比降水尺,同时观测水位,得到瞬时水面纵比降。如水面纵比降测量存在较大误差,此类数据也应被剔除。

依据上述原则对实测数据进行筛选后,最终得到1958—1990年的黄河下游实测阻力资料统计,如表1所示。从表1中可以看出,实测阻力资料涉及黄河下游花园口、高村、利津等7个水文站,共计686组有效数据。这些资料所涉及的范围为,流量Q=8～5 950 m3/s,含沙量S=0.11～169 kg/m3,水深h=0.53～8.37 m,宽深比B/h=16～3 211,床沙中值粒径D50=0.031～0.187 mm,水面纵比降J=0.30×10-4～8.70×10-4,水流弗劳德数Fr=0.05～0.73。

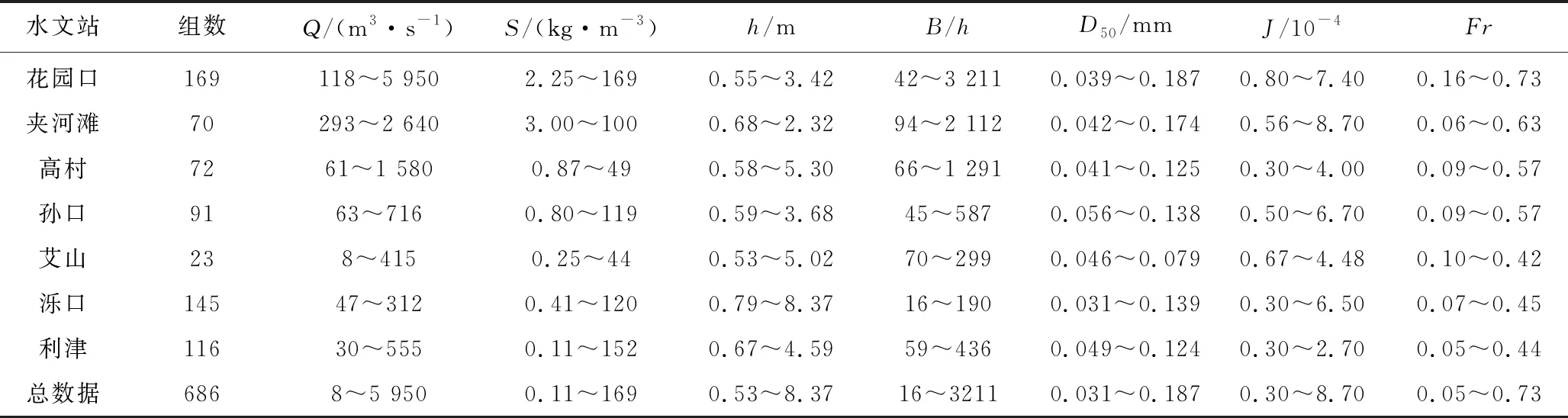
表1 黄河下游各水文站实测水沙资料范围(1958—1990年)

2.2 动床阻力变化特点

黄河下游河床持续冲刷一方面导致床面冲深下切,另一方面促进床沙不断发生分选,床沙粗化明显。花园口站汛后床沙中值粒径由1999年的0.072 mm粗化至2015年的0.263 mm(图3(a))。此外,花园口站2014年各流量级下的糙率系数较1999年有明显增大。图3(b)显示,流量为2 000 m3/s下的糙率系数由1999年的0.013增加至2014年的0.034。在黄河下游持续冲刷过程中,同流量下的过流面积显著增大,水深增加,流速减小,故水流弗劳德数减小,水流能态将从原来的高能态区或者过渡区向低能态区靠近。此外,以花园口水文断面为例,河床冲刷程度越大,出现高能态区所需要的流量越大。张原锋和王平[23]认为黄河下游游荡型河段床面形态主要表现为沙垄、过渡及动平整,且当流量小于1 500 m3/s时床面形态主要表现为沙垄。水流条件及河床组成的改变均会显著影响动床阻力的大小,因此需要结合黄河下游实测水沙资料,研究动床阻力的计算方法。

图3 花园口站床沙粒径及汛期动床阻力系数变化

2.3 动床阻力的影响因素分析

对定床明渠水流而言,当水流属于紊流光滑区时,阻力仅与水流雷诺数(Re)有关,与边界的粗糙程度无关。对于天然冲积河流而言,水流一般都处于紊流阻力平方区,阻力与雷诺数无关,仅是相对粗糙度的函数。对于动床挟沙水流而言,阻力问题相对复杂。研究表明,动床阻力的主要影响因素为水流强度与床面形态等参数[1,17]。

2.3.1 水流强度的影响

反映水流强度的指标很多,这里主要采用能综合反映水流强度的弗劳德数表示。赵连军和张红武[12]根据模型试验结果,通过确定摩阻厚度与弗劳德数等因子之间的经验关系,建立了黄河下游河道糙率系数的计算公式。邓安军等[24]分析了黄河水文站实测资料,发现糙率系数随Fr的增大而减小,两者呈幂函数关系。

针对黄河下游1958—1990年筛选后的实测资料,绘制阻力系数与水流弗劳德数之间的关系,如图4(a)所示。从图中可以看出,两者存在较为明显的幂函数关系,即阻力系数(f)随Fr的增大而减小。由于黄河下游河道宽浅,而水深相对较小,断面平均流速一般不大,水流基本都处于缓流状态,故Fr小于1.0。当Fr<0.3时,随Fr增加阻力系数减小的速率相对较大；当Fr>0.3时,阻力系数减小的速率则相对较小。

图4 阻力系数与不同水沙因子的关系

2.3.2 相对水深的影响

相对水深是影响动床阻力计算的重要因素。Brownlie[16]、Karim[18]及Wang和White[25]都基于相对水深提出了床面形态的判别方法。van Rijn[26]、秦荣昱等[2]及王士强[21]在建立动床阻力公式时都考虑了相对水深的影响。黄才安和严恺[27]则认为大部分动床阻力公式均可以归结为以水流强度、相对水深及无因次粒径为自变量的函数。

此处绘制阻力系数与相对水深的关系,如图4(b)所示。对比图4(b)与图4(a)可以看出,f与h/D50的幂关系不如与Fr的明显,但仍能看出f随h/D50增加而减小的趋势,这与实际情况也相吻合。

2.3.3 含沙量的影响

钱宁等[1]通过分析黄河下游糙率系数n与实测水位、流量及含沙量等单因素的关系,认为同一流量下,n不随含沙量的增大而变化,影响糙率的主要是水流条件,而含沙量对糙率的影响只是一个派生的结果。含沙量对阻力系数的影响主要表现为:含沙量沿垂向分布的不均匀性影响了水流流速的垂向分布特征。卡门常数是表征水流流速垂向分布的参数,可以认为含沙量的变化是通过改变卡门常数来影响流速垂向分布,从而影响阻力系数的大小。惠遇甲等[28]采用黄河、长江等实测资料研究了S对n的影响,结果发现n随S的增大而减小,但由于所用实测资料中含沙量一般不超过45 kg/m3,故所得结论适用范围十分有限。邓安军等[24]通过分析大量天然河道实测资料和水槽试验资料,发现n随S的增加呈先减小后增大的趋势。

点绘f与S的关系,如图4(c)所示。从图中可以看出,尽管两者关系比较分散,但f总体表现出随着S增加而减小的趋势。由于采用的实测资料中S最大值不超过175 kg/m3,且大多数小于100 kg/m3。因此不易判断高含沙水流中含沙量对阻力系数的具体影响。同时考虑到含沙量对糙率影响仅是一个派生的结果[1],故后面分析中暂不考虑含沙量大小对动床阻力的影响。

3 动床阻力公式的建立及率定

3.1 不考虑水流能态分区的动床阻力公式

图4分析表明,阻力系数与弗劳德数、相对水深均呈幂函数关系,考虑到量纲和谐的要求,经分析后选取f作为因变量,Fr和h/D50作为自变量,得到阻力系数的一般表达式:

f=kFra(h/D50)b

(2)

式中:k为系数,a、b为幂次,这些参数需要通过实测资料率定得到。将1958—1990年的686组实测数据中f、Fr和h/D503个变量的数据输入SPSS软件,对式(2)进行多元回归分析并率定相关参数,可以得到阻力系数的具体表达式:

f=0.007Fr-1.472(h/D50)-0.091R2=0.59

(3)

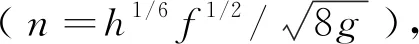
总体来看,选择参数Fr和h/D50作为关键影响因素,基本能够反映动床阻力的变化特点,所建立动床阻力公式的结构形式基本合理。由于没有充分考虑床面形态的影响,未对水流能态进行分区,故式(3)的计算精度相对较低,需要建立基于水流能态分区的动床阻力计算公式。

图5 f及n计算值与实测值比较

3.2 基于水流能态分区的动床阻力公式

3.2.1 水流能态分区方法

随着水流强度的增加,床面形态由静平床发展为沙纹和沙垄,再到动平床、逆波等。一般认为沙纹、沙垄状态称为水流低能态；沙垄消亡趋于动平整状态称为过渡态；动平床以后的状态称为高能态[17,19]。床面阻力随着床面形态的变化也相应改变,不同床面形态的阻力相差很大,床面形态的判别对揭示动床阻力规律有十分重要的意义[22,26]。黄河下游河床组成较细,床沙基本为细沙,抗冲性较差,细沙河流具有易冲易淤的河床演变特点,因此,黄河下游床面形态随着水流强度的变化差异较大。动床阻力不仅受床面粗糙程度影响,还与床面形态密切相关,要精确计算黄河下游的动床阻力,首先要正确判别床面形态。然而床面形态变化过程十分复杂,且野外观测难度较大,因此天然河流的床面形态观测资料十分有限。

目前国内外主要研究成果中床面形态观测数据主要通过水槽试验来获取。本研究收集了Guy等[29]、Brownlie[30]和王士强[17]整理的水槽试验数据及天然河道资料。如前所述,弗劳德数、相对水深及水面比降是判断床面形态的主要参数[17- 18,26]。依据黄河下游各水文站实测床沙粒径及水面比降的资料范围,对水槽和天然河道资料中有床面形态记录的数据进行了筛选,最终选出367组水槽试验数据和67组天然河道资料。这些资料所涉及的D50=0.088～1.460 mm,Fr=0.038～0.880,h/D50=86～14 956,J=0.187×10-4～15.0×10-4。这些资料基本与黄河下游河段的实测资料范围接近,能够包括黄河下游出现的不同床面形态。按照上述434组实测床面形态数据,计算得到各水流能态区量纲一参数Fr和hJ/D50,点绘出Fr和lg(hJ/D50)之间的关系(图6(a))。图6(a)显示,水流低能态区与过渡区有较为清晰的分界线,过渡区与水流高能态区之间的界线略显模糊,但也可近似确定出两区的分界线。由于缺少黄河下游的实测床面形态数据,此方法也存在一定的局限性,需要后续进一步完善。

图6 水流能态分区方法及结果

参考Swamee和Ojha[31]在冲积河流河床形态判别中关于分界线划分的方法,根据图6(a)可初步确定出水流低能态区与过渡区、过渡区与高能态区的分界线,即低能态区的上限方程和高能态区的下限方程:

(4)

由于过渡区点据较少且比较分散,划线时在保证低能态区和高能态区内大部分点据分布正确的情况下,尽可能使过渡区内正确的点数最多。相较于王士强[17]和Guy等[29]提出的水流能态分区方法,式(4)可以直观地划分3个水流能态区,且公式结构相对简单。

3.2.2 公式建立及率定

采用表1中黄河下游花园口、高村及利津等7个水文站共计686组实测数据,利用式(4)判别这些数据点所属的水流能态区,如图6(b)所示。由于本研究收集的主要是汛期数据,故大部分数据点属于过渡区及高能态区。按照水流能态分区的结果,利用各水流能态分区的实测数据,分别对式(2)进行多元非线性回归,可得到水流低能态区、过渡区及高能态区f与n的计算公式:

(5)

根据SPSS的回归结果,式(5)中除了过渡区的参数k值(4.617)外,其余参数的标准误差均小于0.3,置信度较高。式中f与n的计算公式应是等价的,涉及的参数也一致。采用式(5)计算了黄河下游主槽的动床阻力系数,图7分别给出了f及n的计算值与实测值的对比结果。在低能态区、过渡区及高能态区,依据式(5)计算的f与实测值的决定系数分别为0.93、0.93和0.67,相较于不考虑水流能态分区的动床阻力公式,划分能态分区后建立的动床阻力公式的计算精度显著提高。这说明床面形态是影响黄河下游动床阻力计算的关键因素之一。此外,如采用Karim[18]提出的水流能态分区方法重复以上步骤,发现对应于低能态区、过渡区及高能态区的R2分别为0.56、0.19和0.27,这在一定程度上说明已有的一些水流能态分区方法并不能很好地适用于黄河下游阻力计算。

图7 基于水流能态分区的阻力系数f及n计算值与实测值比较

在此基础上统计了水流能态分区后动床阻力公式计算值与实测值的偏离误差。对于f,19.7%的计算值落入实测值的±10%偏离误差之内,50.6%的计算值落入实测值的±30%偏离误差之内;对于n,38.3%的计算值落入实测值的±10%偏离误差之内,83.7%的计算值落入实测值的±30%偏离误差之内。与不考虑水流能态分区的动床阻力公式计算结果相比,分区后公式的计算精度显著提高。

4 动床阻力公式验证

4.1 验证数据来源

为验证基于水流能态分区动床阻力公式的计算精度,收集了黄河下游沿程6个水文站(花园口、高村、利津等)1991—2016年的实测水沙资料。1991—1999年期间黄河下游处于冲淤交替的状态,而1999—2016年期间黄河下游呈持续冲刷状态,因此所选年份的数据具有较好的代表性。根据前述原则对收集的数据进行了筛选,最终得到2 288组实测资料,如表2所示。从表2中可以看到,公式验证采用资料所涉及的范围为:Q=25～7 570 m3/s,S=0.18～224 kg/m3,h=0.48～9.60 m,B/h=18～5 616,D50=0.021～0.267 mm,J=0.20×10-4～8.67×10-4,Fr=0.06～0.68。对比表2与表1,床沙D50、J及Fr的变化范围基本一致,可以确保公式验证的合理性及可靠性。

表2 公式验证采用的黄河下游实测水沙资料范围(1991—2016年)

4.2 验证及结果分析

考虑到工程实际中糙率系数应用较为广泛,此处利用上述实测数据对式(5)中n的计算公式进行验证(图8)。从图8中各站验证结果来看,泺口站数据点相对散乱,大部分数据处于高能态区,其余各站数据点均较为集中地分布在45°对角线两侧。整体而言,验证结果与率定结果较为一致,说明基于水流能态分区动床阻力公式的计算精度较高,可以用于计算黄河下游河道的动床阻力。

图8 黄河下游各水文站糙率系数n计算值与实测值比较

表3统计了水流能态分区后黄河下游各水文站(1991—2016年)糙率系数计算值与实测值的偏离误差、几何标准差、均方根误差及决定系数。从表3可以看出,对于n,27.9%～42.2%的计算值落入实测值的±10% 偏离误差之内,66.4%～88.8%的计算值落入实测值的±30%偏离误差之内。总体来看,验证结果较好,R2=0.50～0.87。因此,本文提出的基于水流能态分区的动床阻力计算公式可以较好地反映黄河下游动床阻力的变化特点,且公式结构简单,所需参数均可在水文站实测资料中获取。

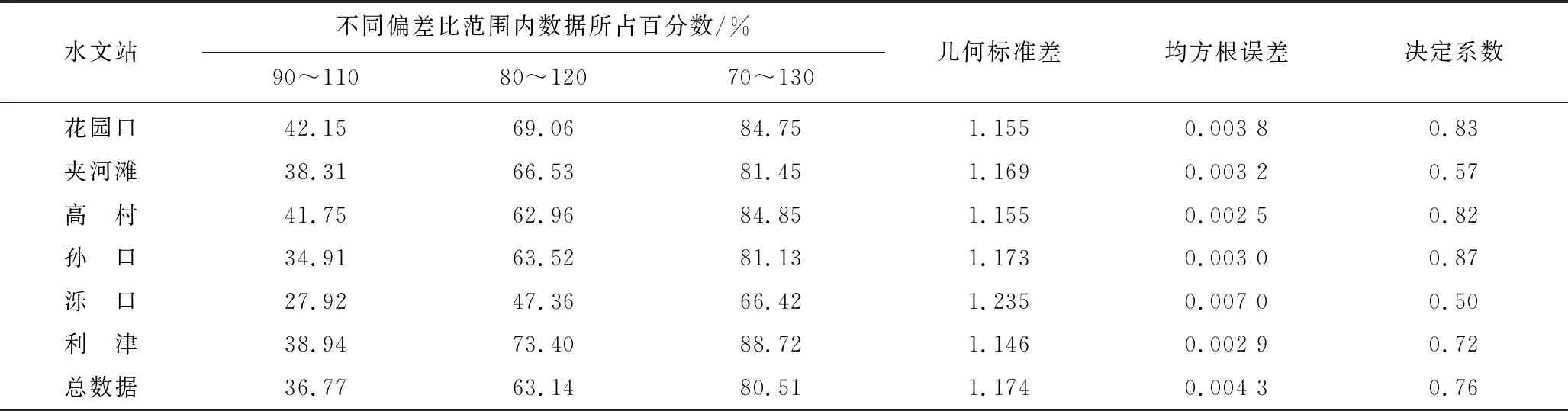
表3 水流能态分区后动床阻力公式的计算精度

此外,本文还选取了van Rijn[26]、王士强[17]、秦荣昱等[2]及赵连军和张红武[12]等提出的动床阻力公式进行计算精度的比较,其中后3个公式经常用于黄河下游动床阻力计算。王士强公式[17]主要用于相对水深大于10 000时天然河流的动床阻力计算。采用黄河下游1991—2016年间的实测资料对以上4个公式进行了验证,并统计了计算精度(表4)。表4显示,针对黄河下游1991—2016年的实测阻力资料,4个公式偏差比小于10%的数据占比均小于20%,van Rijn公式[26]的计算精度相对较高。对比表3和表4可知,式(5)的计算精度较上述4个公式均有明显提升,相较于van Rijn公式[26],计算偏差在±30%以内的数据占比提高了约27%,相较于其他3个公式则至少提高了35%。需要说明的是,van Rijn公式[26]适用于床沙中值粒径介于0.53～1.55 mm时的动床阻力计算,而表2中的床沙中值粒径均小于0.267 mm,这是造成误差的主要原因之一；此外,van Rijn[26]在率定输移状态参数时,大多数点据均分布在区间(0,10)之间,大于10的点据非常少,而根据黄河下游的实测数据计算的输移状态参数大于10的组数约占70%,这也是导致计算误差的重要原因。王士强公式[17]仅适用于f<0.04时的阻力计算,而验证资料中存在较多f>0.04的数据,导致该公式计算误差偏大。

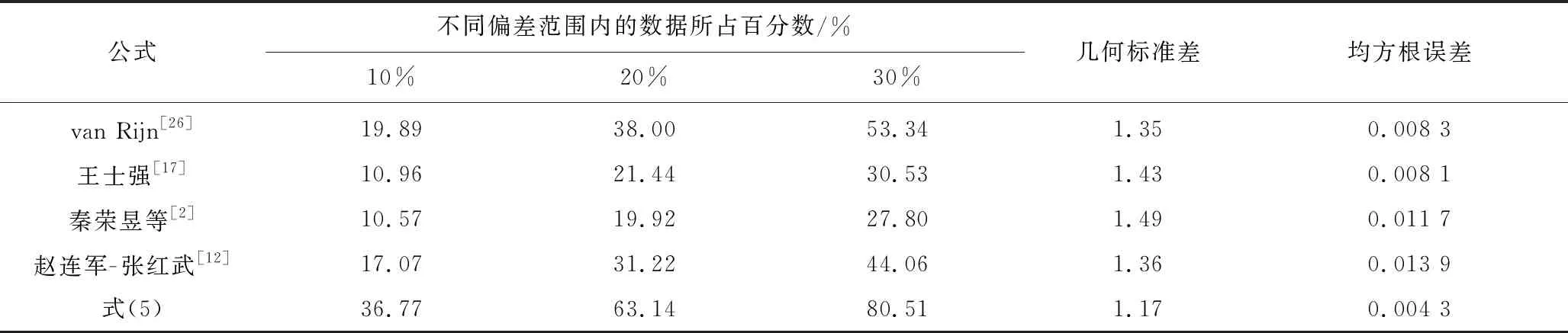
表4 已有代表性阻力公式的计算精度对比

综上所述,当水流条件满足或接近均匀流条件,式(5)可较好地反映黄河下游河道水流条件和床面粗糙度对动床阻力的影响,但该式仅适用于n小于0.06时阻力的计算。此外,该公式没有考虑滩面植被阻力、河槽形态阻力以及各类河道整治工程引起的外加阻力,因此,该式用于数学模型中时仍需要进行适当修正,以考虑这些附加阻力的影响。

5 结 论

本文收集了黄河下游1958—1990年各水文站686组实测有效阻力资料,根据先进行水流能态分区,再建立相应动床阻力计算公式的方法,提出了适用于黄河下游水沙特点与床面形态的动床阻力公式。最后利用黄河下游1991—2016年各水文站2 288组实测水沙资料,对所得计算公式进行验证,得到以下主要结论:

(1) 定量分析了不同水沙因子对黄河下游动床阻力的影响。动床阻力大小随水流弗劳德数(Fr)或相对水深(h/D50)的增加而减小,因此选取Fr与h/D50作为影响动床阻力的关键水沙因子。

(2) 提出了基于水流能态分区的动床阻力计算公式。利用收集到的434组床面形态数据(包括367组水槽试验数据与67组天然河道数据),提出了采用建立量纲一参数Fr与lg(hJ/D50)之间的关系式来划分水流能态分区的方法;以Fr与h/D50为自变量,建立了不同水流能态分区下动床阻力系数f及n的计算公式,并采用2个不同时期黄河下游各水文站的实测资料对公式进行率定与验证。

(3) 基于水流能态分区的动床阻力公式的计算精度明显优于不考虑水流能态分区的公式及其他4个常用动床阻力公式,决定系数总体接近0.80,说明水流强度与床面相对粗糙度对动床阻力影响十分显著。